Сосуд разделен пористой неподвижной перегородкой на две части

1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)

2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)

3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)

4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)

5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)

6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)

7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)

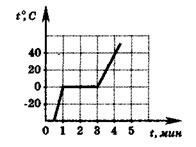8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)

9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)

10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)

11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)

12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)

13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)

14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.

(Решение)

15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)

16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)

17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)

18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)

19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)

(Решение)

20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)

21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)

22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)

23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)

24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)

25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)

26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)

27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)

2017-10-05   
Сосуд с разреженным газом разделен на две части тонкой перегородкой, в которой имеется отверстие, размер которого мал по сравнению со средней длиной свободного пробега (рис. 1). Найти отношение концентрации газа в разных частях сосуда, если в одной из них поддерживается температура $T_{1}$, в другой $T_{2}$.

Решение:

Будем считать, что газ в сосуде идеальный, т. е. его молекулы взаимодействуют между собой только при столкновениях. По условию задачи газ разрежен настолько, что средняя длина свободного пробега молекул между столкновениями много больше размеров отверстия. В этом случае молекулы свободно проходят через отверстие, причем каждая молекула приходит в другую половину сосуда с той же энергией, которой она обладала до этого. Средняя энергия молекул при термодинамическом равновесии определяется температурой. Поэтому переход молекул из одной части сосуда в другую должен приводить к выравниванию температур.

Говорить об определенной температуре газа каждой части сосуда можно только в том случае, когда отверстие в перегородке достаточно маленькое, так что установление термодинамического равновесия в каждой части сосуда происходит гораздо быстрее, чем выравнивание температур этих частей.

Сколько же молекул проходит в единицу времени через отверстие из одной половины сосуда в другую? Нетрудно сообразить, что среднее число таких молекул $N$ пропорционально концентрации $n$ и средней скорости $langle v rangle$ молекул в той половине сосуда, из которой они переходят, а также площади отверстия $S$:

$N = Cn langle v rangle S$. (1)

Для вычисления числового значения безразмерного коэффициента $C$ нужно знать закон распределения молекул по направлениям скорости. Однако для решения этой задачи значение $C$ нам не потребуется.

В стационарном состоянии полное число молекул в каждой половине сосуда не меняется со временем. Поэтому среднее число молекул, проходящих через отверстие слева направо и справа налево, должно быть одинаковым. Отсюда с помощью соотношения (1) получаем

$n_{1} langle v_{1} rangle = n_{2} langle v_{2} rangle$. (2)

Средние скорости молекул в каждой половине пропорциональны квадратному корню из соответствующей температуры. Поэтому из равенства (2) находим

$n_{1}/n_{2} = sqrt{T_{2}/T_{1}}$. (3)

В горячей части сосуда концентрация молекул меньше. Однако давление газа там больше, чем в холодной части. Учитывая, что давление выражается формулой $p = nkT$, с помощью равенства (3) получаем для отношения давлений в разных половинах сосуда

$p_{1}/p_{2} = sqrt{T_{1}/T_{2}}$. (4)

рис.2

Рассмотренные в этой задаче закономерности, связанные с прохождением молекул газа через отверстие, соединяющее сосуды с разной температурой, позволяют объяснить следующий простой, но очень эффектный опыт. Керамический сосуд с пористыми стенками опускается открытым концом в воду (рис. 2). Внутри сосуда находится спираль, при пропускании тока через которую можно нагревать находящийся в сосуде воздух. При включении спирали температура воздуха повышается, он расширяется и начинает выходить пузырями из находящегося подводой отверстия сосуда. При достижении стационарного состояния , когда подводимая спиралью теплота станет равной теплоте, отдаваемой поверхностью сосуда в окружающую среду, в сосуде установится определенная температура. Казалось бы, что при этом выход пузырей воздуха должен прекратиться. Так бы и произошло, если бы стенки сосуда были непроницаемыми для молекул воздуха, например стеклянными или металлическими.

Но если стенки сосуда пористые, то пузырьки воздуха будут выходить все время, даже тогда, когда температура воздуха в сосуде перестанет повышаться! В чем же здесь дело?

Температура воздуха внутри пористого сосуда выше, чем снаружи, в атмосфере. Давление же воздуха там и там практически одинаково: внутри сосуда оно больше атмосферного всего на несколько сантиметров водяного столба, что соответствует глубине погружения отверстия сосуда код воду. Через поры в стенках сосуда происходит непрерывный обмен молекулами между воздухом внутри сосуда и в атмосфере, так же как это происходит в сосуде с отверстием в перегородке, рассмотренным в данной задаче. В замкнутом сосуде в стационарном состоянии число молекул, проходящих через отверстие в обе стороны, одинаково. В результате, как видно из формулы (3), в частях сосуда устанавливались такие концентрации, что произведение концентрации на корень из термодинамической температуры было одинаково: $n sqrt{T} = const$.

В рассматриваемом случае одинаковыми по обе стороны пористой перегородки будут давления воздуха. Так как $p = nkT$, то теперь $nT = const$. Но это означает, что потоки молекул воздуха через поры в стенках из атмосферы в сосуд и обратно неодинаковы. Какой же из них больше? Так как поток молекул пропорционален произведению $n sqrt{T}$ в той части, откуда он идет, то при выполнении условия $nT = const$ он будет больше оттуда, где температура ниже. Это и дает объяснение описанному опыту: поток воздуха через поры внутрь сосуда больше, чем наружу. В результате в стационарном состоянии входящий через поры в сосуд избыточный воздух нагревается, расширяется и выходит в виде пузырей через отверстие.