Сосуд с газом находится в лифте
Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:
Определение
При постоянной массе газа и его неизменной молярной массе отношение произведения давления на объем к его абсолютной температуре остается величиной постоянной:
pVT=const или p1V1T1=p2V2T2
Объединенный газовый закон применительно к изопроцессам
Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.
Определение
Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным.
Изотермический процесс. Закон Бойля — Мариотта.
Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:
m = const (m1 = m2)
T = const (T1 = T2)
Для изотермического процесса действует закон Бойля — Мариотта:
Закон Бойля — Мариотта
Для газа данной массы произведение газа на его объем постоянно, если температура газа не меняется.
pV = const (p1V1 = p2V2)
Изохорный процесс. Закон Шарля.
Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:
m = const (m1 = m2)
V = const (V1 = V2)
Для изохорного процесса действует закон Шарля:
Закон Шарля
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
pT=const (p1T1=p2T2)
Изобарный процесс. Закон Гей-Люссака.
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:
m = const (m1 = m2)
p = const (p1 = p2)
Закон Гей-Люссака
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
VT=const (V1T1=V2T2)
Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.
Так как газ нагревают, то:
T2 – T1 = 240 (К)
Отсюда:
T2 = 240 + T1 (К)
p1 = p
p2 = 1,6p
Запишем закон Шарля применительно к данному случаю:
pT1=1,6p240+ T1
Сделаем некоторые преобразования и вычислим начальную температуру:
pT1=1,6p240+ T1
240+ T1=1,6T1
0,6T1=240
T1=2400,6=400 (К)
Подсказки к задачам на газовые законы
Газ под невесомым поршнем: p = pатм p — давление газа; pатм — давление, оказываемое на газ со стороны поршня. | |
На невесомый поршень действует сила: p=pатм+FS F — сила, действующая на поршень; S — площадь поршня. | |
На невесомый поршень поставили груз. В данном случае на поршень дополнительно будет действовать сила тяжести: p=pатм+FтяжS=pатм+MgS Fтяж — сила тяжести, действующая на поршень со стороны груза; M — масса груза; g — ускорение свободного падения. | |
Газ под массивным поршнем. В данном случае на него дополнительно будет действовать сила тяжести поршня: p=pатм+mgS m — масса поршня. | |
На массивный поршень поставили груз. В данном случае на поршень дополнительно будут действовать силы тяжести со стороны поршня и груза: p=pатм+MgS+mgS | |
На массивный поршень действует сила. В данном случае газ сдавливается как атмосферным давлением, так и силой тяжести поршня, а также силой, которая на него действует: p=pатм+mgS+FS | |
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вверх. Когда ускорение движения лифта противоположно направлено ускорению свободного падения, вес тел увеличивается. Поэтому: p=pатм+mgS+maS a — модуль ускорения, с которым движется лифт. | |
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вниз. Когда ускорение движения лифта направлено в сторону вектора ускорения свободного падения, вес тел уменьшается. Поэтому: p=pатм+mgS−maS | |
«Пузырек у поверхности воды» — на пузырек действует только атмосферное давоение: p = pатм | |
«Пузырек на глубине» — на пузырек действует атмосферное давление и давление столба жидкости: p = pатм + ρgh ρ — плотность жидкости; h — глубина, на которой находится пузырек. | |
Газ, находящийся в горизонтальной пробирке, отделен от атмосферы столбиком ртути. Объем газа можно вычислить, используя параметры пробирки: V1 = l1S V1— объем газа; l1 — длина части пробирки, которую занимает газ; S — площадь поперечного сечения пробирки. Давление газа равно атмосферному давлению: p1 = pатм | |
Пробирку поворачивают открытым концом вверх. В этом случае кроме атмосферного давления на газ давит давление со стороны ртути: P2 = pатм + ρgh Объем газа можно вычислить, используя параметры пробирки: V2 = l2S | |
Пробирку поворачивают открытым концом вниз. В этом случае сумма давлений газа и ртути в пробирке равна атмосферному давлению. Отсюда давление газа равно: P3 = pатм – ρgh Объем газа можно вычислить, используя параметры пробирки: V3 = l3S | |
| Шар или понтон поднимается вверх в воздухе или жидкости | Архимедова сила больше силы тяжести: FA > Fтяж |
Пример №2. Поршень площадью 10 см2 массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с2? Изменение температуры газа не учитывать.
10 см2 = 10–3 м2
20 см = 0,2 м
100 кПа = 105 Па
Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем:
p1=pатм+mgS
Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх:
p2=pатм+mgS+maS
Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно:
p1V1 = p2V2
Объемы в 1 и 2 случае будут определяться формулами:
V1 = Sh1
V2 = Sh2
h1 — расстояние от нижнего края поршня до дна сосуда в первом случае. h2 — та же самая величина, но во втором случае (искомая величина).
Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов:
p1V1=Sh1(pатм+mgS)
p2V2=Sh2(pатм+mgS+maS)
Так как это изотермический процесс, правые части уравнений можно приравнять:
Sh1(pатм+mgS)= Sh2(p атм+mgS+maS)
Отсюда:
Графики изопроцессов
Изопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.
| Изопроцесс | График в координатах (p;V) | График в координатах (V;T) | График в координатах (p;T) |
| Изотермический (график — изотерма) | Изотерма в координатах (p;V) — гипербола. Чем ближе изотерма к началу координат и осям, тем меньшей температуре она соответствует. Характер изменения переменных величин хорошо виден на графике. | Изотерма в координатах (V;T) — прямая, перпендикулярная оси OT и параллельная оси OV. Чем ближе изотерма к оси OV, тем меньшей температуре она соответствует. С увеличением объема давление уменьшается. | Изотерма в координатах (p;T) — прямая, перпендикулярная оси OT и параллельная оси Op. Чем ближе изотерма к оси Op, тем меньшей температуре она соответствует. С увеличением давления объем уменьшается. |
| Изохорный (график — изохора) | Изохора в координатах (p;V) — прямая, перпендикулярная оси OV и параллельная оси Op. Чем ближе изохора к оси Op, тем меньшему объему она соответствует. С увеличением давления увеличивается температура. | Изохора в координатах (V;T) — прямая, перпендикулярная оси OV и параллельная оси OT. Чем ближе изохора к оси OT, тем меньшему объему она соответствует. С увеличением температуры увеличивается давление. | Изохора в координатах (p;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изохоры к оси OT, тем меньшему объему она соответствует. Характер изменения переменных величин хорошо виден на графике. |
| Изобарный (график — изобара) | Изобара в координатах (p;V) — прямая, перпендикулярная оси Op и параллельная оси OV. Чем ближе изобара к оси OV, тем меньшему давлению она соответствует. С увеличением объема температура растет. | Изобара в координатах (V;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изобары к оси OT, тем меньшему давлению она соответствует. Характер изменения переменных величин хорошо виден на графике. | Изобара в координатах (p;T) — прямая, перпендикулярная оси Op и параллельная оси OT. Чем ближе изобара к оси OT, тем меньшему давлению она соответствует. С увеличением температуры объем растет. |
Пример №3. На рисунке представлен график циклического процесса. Вычертить его в координатах (p;T).
Определим характер изменения величин:
- Процесс 1–2. Гипербола — это изотерма. Следовательно T12 = const. В координатах (p;T) изотерма будет выглядеть как прямая, перпендикулярная оси OT.
- Процесс 2–3. Прямая линия, перпендикулярная оси Op — это изобара. Следовательно p23 = const. В координатах (p;T) изобара будет выглядеть как прямая, перпендикулярная оси Op.
- Процесс 3–1. Прямая линия, перпендикулярная оси OV — это изохора. Следовательно V31 = const. В координатах (p;T) изохора будет выглядеть как прямая, выходящая из начала координат.
Теперь, зная, какими будут графики всех величин в координатах (p;T), можно построить сам график. Он примет следующий вид:
Алиса Никитина | ???? Скачать PDF |
Источник
 |

Инструкция по выполнению работы
Задания С1–С6 представляют собой задачи, полное решение которых необходимо записать в бланке ответов № 2. Рекомендуется провести предварительное решение на черновике. При оформлении решения в бланке ответов № 2 запишите сначала номер задания (С1 и т.д.), а затем решение соответствующей задачи.
Полное правильное решение каждой из задач С2–С6 должно включать законы и формулы, применение которых необходимо и достаточно для решения задачи, а также математические преобразования, расчеты с численным ответом и, при необходимости, рисунок, поясняющий решение.
Решив задачу, Вы сможете свериться с образцом, кликнув надпись (Решение) в конце условия задачи.
Желаем успеха!
Здесь приведены справочные данные, которые могут понадобиться вам при выполнении работы.
При ознакомлении с Демонстрационным вариантом следует иметь в виду, что задания, включённые в демонстрационный вариант, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене, приведен в кодификаторе, помещённом на сайтах www.ege.edu.ru и www.fipi.ru.
 С1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь. (Решение)
С1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь. (Решение)
 С2. На гладкой горизонтальной плоскости находится длинная доска массой M = 2 кг. По доске скользит шайба массой m. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы v0 = 2 м/с, а доска покоится. В момент t = 0,8 с шайба перестаёт скользить по доске. Чему равна масса шайбы m? (Решение)
С2. На гладкой горизонтальной плоскости находится длинная доска массой M = 2 кг. По доске скользит шайба массой m. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы v0 = 2 м/с, а доска покоится. В момент t = 0,8 с шайба перестаёт скользить по доске. Чему равна масса шайбы m? (Решение)
 С3. Один моль одноатомного идеального газа совершает процесс 1–2–3, график которого показан на рисунке в координатах p–T. Известно, что давление газа p в процессе 1–2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1–2–3, если его температура T в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К? (Решение). (Система оценивания).
С3. Один моль одноатомного идеального газа совершает процесс 1–2–3, график которого показан на рисунке в координатах p–T. Известно, что давление газа p в процессе 1–2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1–2–3, если его температура T в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К? (Решение). (Система оценивания).
 С4. Во сколько раз увеличится мощность, выделяемая на резисторе R1, при замыкании ключа К (см. рисунок), если R1 = R2 = R3 = 1 Ом, r = 0,5 Ом? (Решение)
С4. Во сколько раз увеличится мощность, выделяемая на резисторе R1, при замыкании ключа К (см. рисунок), если R1 = R2 = R3 = 1 Ом, r = 0,5 Ом? (Решение)
 С5. В однородном магнитном поле с индукцией В,→направленной вертикально вниз, равномерно вращается по окружности в горизонтальной плоскости против часовой стрелки отрицательно заряженный шарик массой m, подвешенный на нити длиной l (конический маятник). Угол отклонения нити от вертикали равен α, скорость вращения шарика равна v. Найдите заряд шарика q. Сделайте рисунок с указанием сил, действующих на шарик. (Решение)
С5. В однородном магнитном поле с индукцией В,→направленной вертикально вниз, равномерно вращается по окружности в горизонтальной плоскости против часовой стрелки отрицательно заряженный шарик массой m, подвешенный на нити длиной l (конический маятник). Угол отклонения нити от вертикали равен α, скорость вращения шарика равна v. Найдите заряд шарика q. Сделайте рисунок с указанием сил, действующих на шарик. (Решение)
С6. Для увеличения яркости изображения слабых источников света используется вакуумный прибор – электронно-оптический преобразователь. В этом приборе фотоны, падающие на катод, выбивают из него фотоэлектроны, которые ускоряются разностью потенциалов Δφ = 15000 В и бомбардируют флуоресцирующий экран, рождающий вспышку света при попадании каждого электрона. Длина волны для света от источника λ1 = 820 нм, а для света, излучаемого экраном, λ2 = 410 нм. Во сколько раз N прибор увеличивает энергию светового излучения, падающего на катод? Считать, что один фотоэлектрон рождается при падении на катод в среднем k = 10 фотонов. Работу выхода электронов Авых принять равной 1 эВ. Считать, что энергия падающих на экран электронов переходит в энергию света без потерь. (Решение)
Источник
| » Кнопка сайта |
| Термодинамика |
А23. Идеальный одноатомный газ находится в закрытом сосуде объёмом 0,6 м3. При охлаждении его внутренняя энергия уменьшилась на 1,8 кДж. В результате давление газа снизилось на |
|
|
|
С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.) |
С1-4. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения. |
|
C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения. |
C3-7.Идеальный одноатомный газ находится в сосуде объемом 1,2 м3 под давлением 4•103 Па. Определите внутреннюю энергию этого газа. Ответ выразите в килоджоулях (кДж). |
C3-8.Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 м3. При нагревании его внутренняя энергия увеличилась на 18 кДж. Насколько возросло давление газа? Ответ выразите в килопаскалях (кПа). |
С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу? |
С3-10. При изобарном нагревании газообразный гелий получил количество теплоты 100 Дж. Каково изменение внутренней энергии гелия? Масса гелия в данном процессе не менялась. |
С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.) |
С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.) |
С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг. |
С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах. |
С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 105 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3•103 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме. |
С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно. |
С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р1 = 4·105 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтp = 3·103 Н. Найдите L. Считать, что сосуд находится в вакууме. |
|
|
С3-20. Теплоизолированный сосуд объемом V = 2 м3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль Аr. Температура гелия Т1 = 300 К, а температура аргона Т2 = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки. |

С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?
 С3-22. На рисунке изображено изменение состояния 1 моль неона. Начальная температура газа 0°С. Какое количество теплоты сообщено газу в этом процессе?
С3-22. На рисунке изображено изменение состояния 1 моль неона. Начальная температура газа 0°С. Какое количество теплоты сообщено газу в этом процессе?
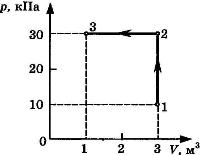 С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
 С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
 С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-26. Одноатомный идеальный газ неизменной массы совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты Qн = 8 кДж. Чему равна работа газа за цикл?
 С3-27. С одноатомным идеальном газом неизменной массы происходит циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
С3-27. С одноатомным идеальном газом неизменной массы происходит циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
С3-28. С разреженным азотом, который находится в сосуде с поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔТ. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔТ. Каким было изменение температуры ΔТ в опытах? Масса азота m = 1 кг.
С3-29. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 = 4•105 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечный объём газа вдвое больше начального. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A = 2493 Дж?
С3-30. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 = 4•105 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечное давление газа p2 = 105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A = 2493 Дж?
С3-31. Один моль одноатомного идеального газа переводят из состояния 1 в состояние 2 таким образом, что в ходе процесса давление газа возрастает прямо пропорционально его объёму. В результате плотность газа уменьшается в α = 2 раза. Газ в ходе процесса получает количество теплоты Q = 20 кДж. Какова температура газа в состоянии 1?
С3-32. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 =4•105 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечное давление газа р2 = 105 Па. Какую работу совершил газ при расширении, если он отдал холодильнику количество теплоты Q = 1247 Дж?
С3-33. В сосуде объёмом V = 0,02 м3 с жёсткими стенками находится одноатомный газ при атмосферном давлении. В крышке сосуда имеется отверстие площадью s, заткнутое пробкой. Максимальная сила трения покоя F пробки о края отверстия равна 100 Н. Пробка выскакивает, если газу передать количество теплоты не менее 15 кДж. Определите значение s, полагая газ идеальным.
 С3-34. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
С3-34. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
| » Вход на сайт |
| » Статистика сайта |
| » Календарь | ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
| » Подготовка к ЕГЭ |
| » Физика. ЕГЭ |
Источник

 С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.
С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь. С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.  С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения. 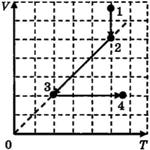 C1-5. Ha VT-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
C1-5. Ha VT-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения. 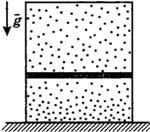 С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.  С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.
С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.