Сосуд с отверстием физика

Закон Торричелли

Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
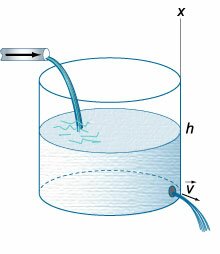
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:

[v = sqrt {2gh} ,]

где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.


Рис.1	Рис.2

Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.

В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)

[v = varphisqrt {2gh} ,]

где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.

Вытекание жидкости из тонкой трубки

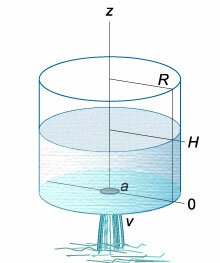
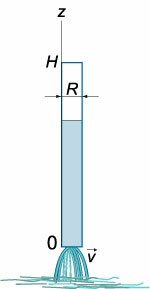
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.

Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть

[v = kh,]

где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.

Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).

Дифференциальное уравнение вытекания жидкости

Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).


Рис.3	Рис.4

Скорость жидкости описывается формулой Торричелли:

[v = sqrt {2gz} ,]

где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:

[q = – pi {a^2}sqrt {2gz} .]

Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.

Уравнение баланса жидкости в резервуаре описывается следующим образом:

[frac{{dV}}{{dt}} = q.]

Поскольку изменение объема (dV) можно выразить как

[dV = Sleft( z right)dz,]

то мы получаем дифференциальное уравнение

[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]

Подставим функцию (qleft( z right)) в это уравнение:

[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]

Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно

[Sleft( z right) = pi {R^2},]

где (R) − радиус основания цилиндра. Тогда

[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]

В результате получаем уравнение с разделяющимися переменными:

[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]

Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)

[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]

Отсюда следует выражение для полного времени вытекания жидкости (T:)

[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]

Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
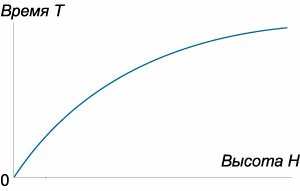
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)

Аналогично можно описать вытекание жидкости и из сосуда другой формы.

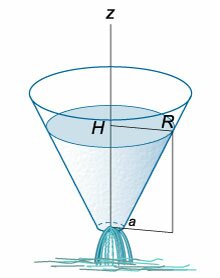
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).


Рис.5	Рис.6

Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением

[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]

где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)

Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:

[qleft( z right) = – pi {a^2}sqrt {2gz} ,]

где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что

[frac{R}{H} = frac{r}{z}.]

Следовательно, площадь поверхности жидкости на высоте (z) будет равна

[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]

Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:

[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]

После простых преобразований получаем следующее дифференциальное уравнение:

[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]

Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)

[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]

Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:

[T = sqrt {frac{{2H}}{g}}. ]

Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?

Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.


Рис.7	Рис.8

Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:

[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]

В данном случае площадь поперечного сечения (Sleft( z right)) является константой:

[Sleft( z right) = S = pi {R^2},]

и поток жидкости, вытекающей из сосуда, определяется формулой:

[qleft( z right) = – kz,]

где (k) зависит от размера отверстия, смачиваемости и других параметров.

В результате получаем простое дифференциальное уравнение:

[pi {R^2}frac{{dz}}{{dt}} = – kz,]

или после разделения переменных:

[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]

Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)

[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]

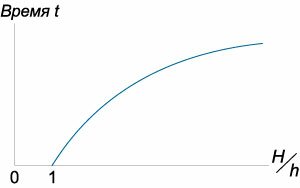
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)

Источник

2017-10-05
Сосуд с разреженным газом разделен на две части тонкой перегородкой, в которой имеется отверстие, размер которого мал по сравнению со средней длиной свободного пробега (рис. 1). Найти отношение концентрации газа в разных частях сосуда, если в одной из них поддерживается температура $T_{1}$, в другой $T_{2}$.

Решение:

Будем считать, что газ в сосуде идеальный, т. е. его молекулы взаимодействуют между собой только при столкновениях. По условию задачи газ разрежен настолько, что средняя длина свободного пробега молекул между столкновениями много больше размеров отверстия. В этом случае молекулы свободно проходят через отверстие, причем каждая молекула приходит в другую половину сосуда с той же энергией, которой она обладала до этого. Средняя энергия молекул при термодинамическом равновесии определяется температурой. Поэтому переход молекул из одной части сосуда в другую должен приводить к выравниванию температур.

Говорить об определенной температуре газа каждой части сосуда можно только в том случае, когда отверстие в перегородке достаточно маленькое, так что установление термодинамического равновесия в каждой части сосуда происходит гораздо быстрее, чем выравнивание температур этих частей.

Сколько же молекул проходит в единицу времени через отверстие из одной половины сосуда в другую? Нетрудно сообразить, что среднее число таких молекул $N$ пропорционально концентрации $n$ и средней скорости $langle v rangle$ молекул в той половине сосуда, из которой они переходят, а также площади отверстия $S$:

$N = Cn langle v rangle S$. (1)

Для вычисления числового значения безразмерного коэффициента $C$ нужно знать закон распределения молекул по направлениям скорости. Однако для решения этой задачи значение $C$ нам не потребуется.

В стационарном состоянии полное число молекул в каждой половине сосуда не меняется со временем. Поэтому среднее число молекул, проходящих через отверстие слева направо и справа налево, должно быть одинаковым. Отсюда с помощью соотношения (1) получаем

$n_{1} langle v_{1} rangle = n_{2} langle v_{2} rangle$. (2)

Средние скорости молекул в каждой половине пропорциональны квадратному корню из соответствующей температуры. Поэтому из равенства (2) находим

$n_{1}/n_{2} = sqrt{T_{2}/T_{1}}$. (3)

В горячей части сосуда концентрация молекул меньше. Однако давление газа там больше, чем в холодной части. Учитывая, что давление выражается формулой $p = nkT$, с помощью равенства (3) получаем для отношения давлений в разных половинах сосуда

$p_{1}/p_{2} = sqrt{T_{1}/T_{2}}$. (4)

Сосуд с отверстием физика
рис.2

Рассмотренные в этой задаче закономерности, связанные с прохождением молекул газа через отверстие, соединяющее сосуды с разной температурой, позволяют объяснить следующий простой, но очень эффектный опыт. Керамический сосуд с пористыми стенками опускается открытым концом в воду (рис. 2). Внутри сосуда находится спираль, при пропускании тока через которую можно нагревать находящийся в сосуде воздух. При включении спирали температура воздуха повышается, он расширяется и начинает выходить пузырями из находящегося подводой отверстия сосуда. При достижении стационарного состояния , когда подводимая спиралью теплота станет равной теплоте, отдаваемой поверхностью сосуда в окружающую среду, в сосуде установится определенная температура. Казалось бы, что при этом выход пузырей воздуха должен прекратиться. Так бы и произошло, если бы стенки сосуда были непроницаемыми для молекул воздуха, например стеклянными или металлическими.

Читайте также: Сосуды у человека фото

Но если стенки сосуда пористые, то пузырьки воздуха будут выходить все время, даже тогда, когда температура воздуха в сосуде перестанет повышаться! В чем же здесь дело?

Температура воздуха внутри пористого сосуда выше, чем снаружи, в атмосфере. Давление же воздуха там и там практически одинаково: внутри сосуда оно больше атмосферного всего на несколько сантиметров водяного столба, что соответствует глубине погружения отверстия сосуда код воду. Через поры в стенках сосуда происходит непрерывный обмен молекулами между воздухом внутри сосуда и в атмосфере, так же как это происходит в сосуде с отверстием в перегородке, рассмотренным в данной задаче. В замкнутом сосуде в стационарном состоянии число молекул, проходящих через отверстие в обе стороны, одинаково. В результате, как видно из формулы (3), в частях сосуда устанавливались такие концентрации, что произведение концентрации на корень из термодинамической температуры было одинаково: $n sqrt{T} = const$.

В рассматриваемом случае одинаковыми по обе стороны пористой перегородки будут давления воздуха. Так как $p = nkT$, то теперь $nT = const$. Но это означает, что потоки молекул воздуха через поры в стенках из атмосферы в сосуд и обратно неодинаковы. Какой же из них больше? Так как поток молекул пропорционален произведению $n sqrt{T}$ в той части, откуда он идет, то при выполнении условия $nT = const$ он будет больше оттуда, где температура ниже. Это и дает объяснение описанному опыту: поток воздуха через поры внутрь сосуда больше, чем наружу. В результате в стационарном состоянии входящий через поры в сосуд избыточный воздух нагревается, расширяется и выходит в виде пузырей через отверстие.

Источник

Тема. Решение задач по теме “Гидростатика и гидродинамика”.

Цели:

– рассмотреть основные приемы решения расчетных задач на тему “Гидростатика и гидродинамика”.

Ход занятия

В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач.

Прежде чем приступить к выполнению задания, следует повторить основные законы гидромеханики.

Основной закон гидростатики – закон Паскаля, согласно которому в состоянии равновесия давление жидкости в данной точке не зависит от ориентации площадки, на которую она действует.

Поскольку в школьном курсе рассматривается стационарное течение несжимаемой жидкости, то будет справедливо уравнение неразрывности струи.

Для идеальной жидкости выполняется уравнение Бернулли. Покажите, что уравнение Бернулли является следствием закона сохранения энергии.

Качественные задачи

К концам равноплечного рычага подвесили две одинаковые гири. Что произойдет, если одну гирю поместить в воду, а другую в керосин?
Ответ: равновесие нарушится.
Почему, если близко стоишь около быстро идущего поезда, возникает эффект “притягивания” к колесам?
Ответ: проходящий поезд увлекает за собой примыкающие к нему слои воздуха. Воздух, движущийся между человеком и поездом, оказывает на него меньшее давление, чем неподвижный. Эта разность давлений и обусловливает силу, увлекающую человека к поезду.
При испытании реактивного снаряда, установленного в хвосте самолета для защиты его от нападения сзади, был обнаружен удивительный факт: при пуске снаряд разворачивался и догонял свой самолет. Как можно объяснить это явление?
Проделайте эксперимент. Вложите в воронку бумажный фильтр (рис. 1) и попробуйте выдуть его через узкий конец воронки. У вас не получилось? Почему?
Ответ: чем сильнее вы вдуваете воздух, тем плотнее фильтр входит в воронку. Объясняется это с помощью закона Бернулли, согласно которому давление понижается в местах сужения. В узком просвете между воронкой и бумажным фильтром давление понижается, и внешнее атмосферное давление удерживает фильтр в воронке.

Примеры решения расчетных задач

Задача 1. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S1, сечение струи S2 (рис. 2). Найдите ускорение, с которым перемещается уровень воды в сосуде.

Решение:

Будем считать жидкость несжимаемой. Тогда для каждого момента времени, согласно уравнению неразрывности струи, можно записать

S1v1 = S2v2, (1)
где v1 – скорость воды в сосуде, v2 – скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1)

,
где – ускорение воды в сосуде, – ускорение свободного падения, так на выходе из сосуда вода начинает свободно падать. Таким образом,

Ответ: .

Задача 2. В сосуде с жидкостью сделано отверстие площадью S. Размеры отверстия малы по сравнению с высотой столба жидкости. В одном случае отверстие закрыто пластинкой и измеряется сила давления жидкости на пластинку F1 при высоте столба жидкости h (рис. 3). В другом случае тот же сосуд стоит на тележке, отверстие открыто, и измеряется сила отдачи F2 при установившемся токе жидкости в момент, когда высота столба жидкости будет та же, что и в первом случае. Будут ли силы F1 и F2 равны?

Решение:

Согласно закону Паскаля давление на жидкость передается во всех направлениях одинаково, поэтому в первом случае давление, производимое на пластинку жидкостью, равно гидростатическому давлению столба жидкости высотой h, а значит, F1 = ρghS , где ρ – плотность жидкости.

Во втором случае сила F2 согласно второму закону Ньютона равна изменению импульса жидкости в единицу времени

.
Изменение импульса Δp = Δmv , где Δm – масса жидкости, вытекающей в единицу времени, v – скорость истечения жидкости из отверстия.

Масса вытекающей жидкости Δm = ρgS, скорость истечения согласно формуле Торричелли . Следовательно,

F2 = ρv2S = 2ρghS.

Таким образом, F2 = 2F1 . Объяснить это можно так. Когда жидкость вытекает из малого отверстия, линии тока вблизи него сгущаются, а значит, как следует из уравнения Бернулли, давление на стенку вблизи отверстия уменьшается. Поэтому сила реакции вытекающей струи оказывается больше силы статического давления на площадь отверстия.

Ответ: силы F1 и F2 не равны.

Задача 3. Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b (рис. 3). Сколько воды вытечет из крана за время t?

Решение:
Воспользуемся условием стационарности течения несжимаемой жидкости

. (1)
Для идеальной жидкости справедливо уравнение Бернулли:

.
Поскольку жидкость свободно падает, то давления в обоих сечениях одинаковы, и уравнение Бернулли принимает вид:

. (2)
За время t через любое сечение протекает один и тот же объем воды, поэтому можно записать

. (3)
Выразим скорость v1 из (1) и (2):

.
Подставим полученное значение v1 в (3) и получим окончательный ответ:

Ответ: .

Задача 4. Площадь поршня в шприце S1 = 2 см2, а площадь отверстия S2 = 1 мм2 (рис. 4). Сколько времени будет вытекать вода из шприца, если действовать на поршень с силой F = 5 H и если ход поршня l = 5 см?

Решение:

Так как из шприца вытечет вся находившаяся в нем жидкость, то

S1l = S2v2t, (5)
где v2 – скорость истечения струи. Будем считать жидкость идеальной, тогда можно использовать уравнение Бернулли:

.
Шприц расположен горизонтально, следовательно, h = const. Уравнение Бернулли тогда запишется следующим образом:

, (6)
где Ра – атмосферное давление, а v1 – скорость движения поршня. Из уравнения неразрывности следует

S1v1 = S2v2. (7)
Решая совместно уравнения (6) и (7), получим

,
отсюда

.
Подставляя найденное значение v2 в (5), получим

.
Так как S2S1 , то можно записать

Ответ:

Задачи для самостоятельной работы

“Вечерело. Уставший за нелегкий трудовой день Абдулла Ибн Сауд присел на берегу реки и стал обдумывать свой социальный статус. В колхоз не берут, кооперативы эмир разогнал, к нему самому на службу устраиваться – так стражники без золотых во дворец не пускают. Эх, жизнь… Но тут взгляд Абдуллы остановился: по реке плыл какой-то предмет, и лишь маленький кусочек сургуча был виден над водой. Абдулла бросился в воду и вытащил оттуда старинный глиняный кувшин, герметично закупоренный сургучом. Распечатав кувшин и перевернув его, Абдулла обомлел: сверкнуло золото. Из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а сосуд запечатал и бросил обратно в воду. Поплыл сосуд дальше, примерно треть его объема торчало над водой”.
Так говорится в одной из восточных сказок. Предполагая, что кувшин был двухлитровый, оцените массу одной золотой монеты.
Ответ: m = 4,45 г.
На некоторых железных дорогах пополнение паровозного котла водой производится без остановки паровоза. Для этой цели применяется изогнутая под прямым углом труба, которая опускается на ходу паровоза в канаву с водой, проложенную вдоль рельсов. При какой скорости паровоза вода может подняться на высоту 3 м?
Ответ: v = 28 км/ч.
Из поднятого на высоту h резервуара выходит труба постоянного сечения S, переходящая в короткую трубу сечением S1, перекрытую краном. Найдите давление в магистральной трубе при открытом кране.
Ответ: Р = Ратм + ρgh.
Определите расход воды Q, протекающей через слив плотины, имеющей ширину l, глубину потока d и понижение уровня потока по сравнению с уровнем воды в водохранилище, равное h.
Ответ: Q = ρdl·√(2gh).
Какова примерно скорость катера, если при его движении вода поднимается вдоль его носовой части
на высоту h = 1 м?
Ответ: v ≈ √(2gh) ≈ 4,4 м/с.
На гладкой горизонтальной поверхности стоит цилиндрический сосуд с водой. В боковой стене сосуда у дна имеется отверстие площадью S0. Какую силу нужно приложить к сосуду в горизонтальном направлении, чтобы удержать его в равновесии? Площадь поперечного сечения сосуда равна S, высота столба жидкости h.
Ответ: .
На поршень шприца площади S действует сила F. С какой скоростью v должна вытекать в горизонтальном направлении струя из отверстия иглы площади s? Плотность жидкости ρ. Трением пренебречь.
Ответ: . Если s S, то .

Рекомендуемая литература

Бутиков Е.И., Кондратьев А.С. Физика. Т. 1. Механика. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 332-352.
Физика. Механика / Под ред. Г.Я. Мякишева. – М.: Просвещение, 1995. – С. 420-436.
Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 63-67.
Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр “Март”, 2004. – С. 184-212.

Источник