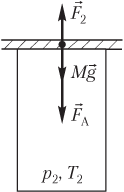Сосуд с поршнем формула

2017-10-05 ![]()
Расположенный горизонтально цилиндрический сосуд, заполненный идеальным газом, разделен поршнем, который может двигаться без трения. В равновесии поршень находится посредине цилиндра. При малых смещениях из положения равновесия поршень совершает колебания. Найти зависимость частоты этих колебаний от температуры, считая процесс изотермическим.
Решение:
В положении равновесия давление $p$ на поршень слева и справа одинаково. Поскольку объем газа слева и справа одинаков, а температура $T$ постоянна, из уравнения Менделеева — Клапейрона
$pV = nu RT$ (1)
следует, что количество газа $nu$ одинаково по обе стороны от поршня. Отметим, что химический состав газов может быть различным.

рис.1
Пусть поршень сместился из положения равновесия, например влево, на малую величину $x$, так что $Sx ll V$, где $S$ — площадь поршня (рис. 1). Поскольку температура по условию не меняется, то
$(p + Delta p_{1})(V – Sx) = (p – Delta p_{2}) (V + Sx)$.
Раскрыв скобки и приведя подобные члены, получим
$( Delta p_{1} + Delta p_{2}) V – ( Delta p_{1} – Delta p_{2}) Sx = 2pSx$.
Второе слагаемое слева много меньше первого не только потому, что $Sx ll V$, но и вследствие того, что множителем при $V$ стоит сумма двух близких величин $Delta p_{1}$ и $Delta p_{2}$, а множителем при $Sx$ — их разность. Пренебрегая вторым слагаемым, получаем
$Delta p_{1} + Delta p_{2} = frac{2pS}{V} x$.
Результирующая сила, действующая на поршень, равна
$F = – frac{2pS^{2}}{V} x$.
Знак минус означает, что сила направлена в сторону, противоположную направлению смещения поршня, т. е. к положению равновесия. Под действием силы, пропорциональной смещению, поршень массой $M$ будет совершать гармонические колебания с частотой $omega$, определяемой соотношением
$omega^{2} = 2pS^{2}/VM$. (2)
При решении задачи мы молчаливо предполагали, что масса газа много меньше массы поршня, так что кинетической энергией макроскопического движения газа при колебаниях поршня можно пренебречь но сравнению с кинетической энергией поршня. Подумайте, где использовано это условие.
Выразив $p$ из уравнения Менделеева — Клапейрона (1), получим
$omega^{2} = frac{2 nu RS^{2}}{MV^{2}} T$. (3)
Таким образом, частота колебаний поршня пропорциональна $sqrt{T}$, ибо коэффициент при $T$ в формуле (3) не зависит от температуры, если пренебречь тепловым расширением сосуда.
Подумайте теперь, какие условия должны выполняться, чтобы процесс действительно был изотермическим. Для того чтобы температура газа в процессе колебаний не изменялась, необходим хороший тепловой контакт с большим тепловым резервуаром — термостатом, имеющим постоянную температуру. Что значит хороший тепловой контакт? Это значит, что время установления термодинамического равновесия между газом в сосуде и термостатом должно быть много меньше периода колебаний поршня. Тогда можно считать, что газ в каждый момент имеет ту же температуру, что и термостат. Если, наоборот, период колебаний окажется много меньше времени установления термодинамического равновесия между газом и термостатом, то можно считать, что колебания поршня происходят практически без обмена теплотой с термостатом. В этом случае процесс можно считать адиабатическим, несмотря на отсутствие тепловой изоляции сосуда с поршнем. Оказывается, что зависимость частоты колебаний от температуры при этом будет такой же, как и в изотермическом случае, только коэффициент в формуле (3) умножится на число, большее единицы. Увеличение частоты колебаний при адиабатическом процессе можно объяснить, сравнивая $p-V$ – диаграммы изотермического и адиабатического процессов идеального газа.
Отметим, что приведенное решение в обоих случаях имеет смысл, только если время установления теплового равновесия в самом газе много меньше периода колебаний поршня, так как в противном случае вообще теряют смысл такие равновесные макроскопические характеристики газа, как давление и температура. Другими словами, по отношению к самому газу процесс должен быть квазистатическим.
Источник
5.4. Практическое применение уравнения состояния идеального газа
5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем
Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
m = const;
- постоянным остается также количество вещества (газа):
ν = const;
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
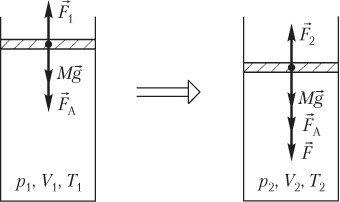
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).
Рис. 5.9
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p1V1=νRT1,p2V2=νRT2,}
где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
Mg+FA=F1,Mg+FA+F=F2,}
где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
T ≠ const;
- если процесс происходит медленно, то температура газа остается постоянной –
T = const.
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
M = 0;
- в остальных случаях поршень обладает определенной ненулевой массой —
M ≠ const.
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.
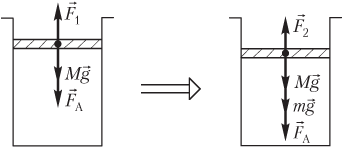
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→1, действующая со стороны газа (до его сжатия);
- сила давления газа F→2, действующая со стороны газа (после его сжатия);
- mg→ — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
F
1 = Mg + F
A,
где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F
2 = Mg + F
A
+ mg,
где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
p
1V
1 = νRT,
где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
p
2V
2 = νRT,
где V
2 — объем сжатого поршнем газа.
Равенство
p
1V
1 = p
2V
2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}
которую требуется решить относительно массы гирь m.
Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:
p2p1=Mg+pAS+mgMg+pAS
и из третьего уравнения:
p2p1=V1V2,
запишем равенство правых частей полученных отношений:
Mg+pAS+mgMg+pAS=V1V2.
Отсюда следует, что искомая масса определяется формулой
m=(M+pASg)(V1V2−1).
Вычисление дает результат:
m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→2, действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
F
2 = Mg + F
A,
где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
p
1V = νRT
1,
где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
p
2V = νRT
2,
где p
2 — давление нагретого газа; T
2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}
систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.
Для этого делением первой пары уравнений
pAVp2V=νRT1νRT2
получим выражение для давления нагретого газа:
p2=pAT2T1
и подставим его в третье уравнение системы:
pAT2ST1=Mg+pAS.
Преобразуем полученное выражение к виду
T2=T1(Mg+pAS)pAS=T1(MgpAS+1),
а затем найдем разность
ΔT=T2−T1=MgT1pAS.
Произведем вычисление:
ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
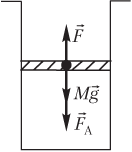
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→, действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:
F→+F→A+Mg→=ma→,
или в проекции на вертикальную ось —
F − F
A − Mg = Ma,
где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a=F−FA−MgM=(p−pA)SM−g.
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
l=v22a,
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
v=2al
и подставим в записанную формулу выражение для модуля ускорения:
v=2l((p−pA)SM−g).
Выполним расчет:
v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Источник
25. Молекулярная физика (Расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 3 л при температуре +70 (^{circ})С находится смесь воздуха с водяными парами. Давление в сосуде равно 99,2 кПа, относительная влажность воздуха 50(%). Давление насыщенного водяного пара при данной температуре равно 31,1 кПа. Какое количество воздуха находится в сосуде? Ответ выразите в миллимолях и округлите до целого числа.
Влажность воздуха: [varphi=dfrac{p_{text{вод.пар}}}{p_{text{нас.пар}}} ; ; ; Rightarrow ; ; ; p_{text{вод.пар}}=varphi cdot p_{text{нас.пар}}] где (p_{text{вод.п.}}) — давление водяных паров, (p_{text{н.п.}}) — давление насыщенных паров. [p_{text{вод.пар}}=0,5cdot31,1text{ кПа}=15,55 text{ кПа}] По закону Дальтона, давление смеси равно сумме парциальных давлений компонентов: [p_{text{см}}=p_1+p_2+dots+p_n] [p_{text{см}}=p_{text{возд}}+p_{text{вод.пар}} ; ; ; Rightarrow ; ; ; p_{text{возд}}=p_{text{см}}-p_{text{вод.пар}}] [p_{text{возд}}=99,2text{ кПа}-15,55text{ кПа}=83,65 text{кПа}] Запишем уравнение Менделеева – Клапейрона для воздуха: [p_{text{возд}}V=nu RT] где (V) — объем газа, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа в Кельвинах.
Вырразим количесвто веещества: [nu=dfrac{p_{text{возд}}V}{RT}] [nu=dfrac{83,65cdot10^3text{ Па}cdot3cdot10^{-3}text{ м}^3}{8,31text{ Дж/(моль$cdot$К)}cdot(70+273)text{ К}} approx 88 text{ ммоль}]
Ответ: 88
В большом сосуде с жёсткими стенками, закрытом подвижным поршнем, находятся воздух и насыщенный водяной пар при температуре 100 (^{circ})С. Давление в сосуде равно 150 кПа. Поршень переместили, поддерживая температуру содержимого сосуда постоянной. При этом половина водяного пара сконденсировалась. Какое давление установилось в сосуде? Ответ выразите в кПа.
В сосуде находятся воздух и насыщенный пар, при этом давление в сосуде состоит из суммы давлений этих двух газов: [p=p_1+p_2] Так как водяной пар насыщенный, то его давление при 100 (^{circ})С равно 100 кПа: (p_1) = 100 кПа.
Тогда давление воздуха равно: [p_2=150text{ кПа}-100text{ кПа}=50text{ кПа}] Половина водяного пара сконденисровалась, это означает, что объем уменьшили в 2 раза.
Давление водяных паров не изменилось, так как пар насыщенный.
Давление воздуха увеличилось в 2 раза, потому что объем уменьшился в 2 раза, температура не меняется.
Таким образом, давление в конечном сосстоянии в сосуде: [p=p_1+p’_2] [p =100text{ кПа}+50text{ кПа}cdot2=200 text{ кПа}]
Ответ: 200
В закрытом сосуде находится 4 г водяного пара под давлением 50 кПа и при температуре 100 (^{circ})С. Не изменяя температуры, объём сосуда уменьшили в 4 раза. Найдите массу образовавшейся при этом воды. Ответ приведите в граммах.
Влажность воздуха: [varphi=dfrac{p_{text{вод.пар}}}{p_{text{нас.пар}}}] где (p_{text{вод.п.}}) — давление водяных паров, (p_{text{нас.п.}}) — давление насыщенных паров.
Давление насыщенного водяного пара при 100 (^{circ})С равно 10(^5) Па.
Так как объем умеьшился в 4 раза, а максимальное давление (10^5) Па (100 кПа), то давление может увеличиться только в 2 раза.
Запишем уравнение Менделеева – Клапейрона для водяного пара: [p_{text{вод.пар}}V=dfrac{m}{mu} RT] где (mu) — молярная масса газа, (V) — объем газа, (m) — масса пара, (R) — универсальная газовая постоянная, (T) — температура пара в Кельвинах.
Из закона видно, что для уменьшения объема в 4 раза (так как давление увеличится в 2 раза) необходимо уменьшение массы водяного пара в 2 раза (то есть половина водяного пара сконденсируется): [m_{text{вод}}=dfrac{m_{text{пар}}}{2}=2text{ г}]
Ответ: 2
В сосуде под поршнем находится 3г водяного пара под давлением 25 кПа при температуре 100 (^circ)С. Объем сосуда изотермически уменьшили в 3 раза, найдите массу образовавшейся воды. Ответ дайте в граммах.
Давление насыщенных паров при 100 (^circ)С равно 100кПа. Найдем влажность пара в сосуде по формуле: [phi=dfrac{p}{p_text{ н.п.}}100%] где (p) — давление газа, (p_text{ н.п.}) — давление насыщенных паров при данной температуре.
Так как объем сосуда изотермически уменьшили, то по закону Бойля – Мариотта: (pV=const), где (V) объем газа.
А значи, при уменьшении объема в 3 раза, давление возрастает в 3 раза.
Тогда влажность равна: [varphi=dfrac{3cdot 25text{ кПа}}{100text{ кПа}}cdot100%=75%] Так как влажность меньше 100% то водяные пары не будут конденсироваться, а значит масса водяного пара не будет увеличиваться.
Ответ: 0
В начальный момент времени газ имел давление (p) = 1(cdot)10(^5) Па при (t) = 100 (^{circ})С. Затем газ изотермически сжали в (k) = 4 раз. В результате давление газа увеличилось в 2 раза. Определите относительную влажность в начальный момент времени. Потерями вещества пренебречь. Ответ дайте в процентах.
Давление насыщенного водяного пара при 100 (^{circ})С равно 10(^5) Па.
Так как объем умеьшился в 4 раза, а давление увиличилось только в 2 раза, то это означает, что часть пара сконденсировалось и пар стал насыщенным, то есть: [p_{text{вод.пар}}=p_{text{нас.пар}}=100text{ кПа}] где (p_{text{вод.пар}}) — давление водяных паров, (p_{text{нас.пар}}) — давление насыщенных паров.
Суммарное конечное давление равно: [p_2=2p_1= 2p] [p_2 = 2cdot1cdot10^5text{ Па} = 200 text{ кПа}] По закону Дальтона, давление смеси равно сумме парциальных давлений компонентов: [p_{text{см}}=p_1+p_2+dots+p_n] [p_{text{см}}=p_{text{возд}}+p_{text{вод.пар}} ; ; ; Rightarrow ; ; ; p_{text{возд}}=p_{text{см}}-p_{text{вод.пар}}] [p_{text{возд}} = 200text{ кПа}-100text{ кПа}=100 text{кПа}] Процесс сжатия воздуха является изотермическим (по условию), значит в начальный момент давление воздуха было в 4 раза меньше: [p_{o_{text{возд}}}=dfrac{100cdot10^3text{ Па}}{4}=25 text{ кПа}] [p_{text{см}}=p_{text{возд}}+p_{text{вод.пар}}] [p_{o_{text{вод.пар}}}=p_{o_{text{см}}}-p_{o_{text{возд}}}] [p_{o_{text{вод.пар}}}=100text{ кПа}-25text{ кПа}=75 text{ кПа}]
Найдем влажность воздуха: [varphi=dfrac{p_{text{вод.пар}}}{p_{text{нас.пар}}}] [varphi=dfrac{75text{ кПа}}{100text{ кПа}}=0,75=75%]
Ответ: 75
Источник