Сосуд с водой подвешен на длинных нитях
29. Механика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вертикальная труба с поршнем, плотно прилегающим к ее внутренним стенкам, опущена нижним концом в воду. Вначале поршень находился в самом нижнем положении, на уровне воды, а затем его медленно поднимают на высоту 20 м. Пренебрегая трением, найдите совершенную при этом работу (в кДж). Площадь поршня 100 см(^2). Атмосферное давление 100 кПа.
Процесс поднятия поршня происходит в 2 этапа. Первый этап: давление под поршнем будет положительным и равное [p_0-rho g h] где (rho) – плотность воды, (h) – высота подъеда поршня.
Вода будет заполнять весь объем под поршнем, а приложенная к поршню сила будет компенсировать давление внутри, она будет равна [F=rho g h S] Она будет линейно возрастать. Это будет до момента, пока вода не поднимется на высоту, равную [h_0=dfrac{p_0}{rho g}=dfrac{100text{ кПа}}{1000text{ кг/м$^3$ cdot 10 Н/кг}}=10text{ м}] При подъеме поршня на высоту (h_0) давление станет равным нулю. После этого вода перестает подниматься, а сила, приложенная к поршню, остается равной [F’=rho g h_0 S=p_0S] Работа по поднятию равна сумме работ: работе по поднятию до высоты (h_0) (A_0=dfrac{0+F_1}{2}h_0=dfrac{p_o S h_0}{2}) (так как она линейно возрастает, то берем как среднее арифметическое от начального, до конечного) и работе по поднятию от высоты (h_0) и конечной высоты (A_1=F_1(h_1-h_0)=p_o Sh_1-p_o Sh_0). Значит полная работа равна [A=dfrac{p_o S h_0}{2}+ p_0 S h_1 -p_0 Sh_0=p_0 S (h_1 -dfrac{h_0}{2})=100text{ кПа}cdot 10^{-2}text{ м$^2$}(20text{ м}-5text{ м})=15text{ кДж}]
Ответ: 15
Шар, до половины погруженный в воду, лежит на дне сосуда и оказывает на него давление с силой, равной 1/3 действующей на него силы тяжести. Найти плотность материала шара.
Сила давления на дно будет равна разности силы тяжести и силы Архимеда, действующих на шар [N=m g-rho_{0} g frac{V}{2},] где (N) – сила давления на дно, (m) – масса шарика,(rho_0) – плотность воды, (V) – объем шарика [N=frac{1}{3} m g] Масса шарика же равна [m=rho V,] где (rho) – плотность материала, из которого сделан шар. Подставим (2) и (3) в (1) и получим [frac{1}{3} rho g V=rho g V-rho_{0} g frac{V}{2}] Откуда плотность тела [rho=frac{3}{4} rho_{0}=frac{3}{4} 1000 text{ кг/м$^3$}=750 text{ кг/м$^3$}]
Ответ: 750
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см(^2). В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой (T). Если нить перерезать, то шар всплывёт, а уровень воды изменится на (h) = 5 см. Найдите силу натяжения нити (T).
“Демоверсия 2018”
Пусть (rho) – плотность жидкости, (H) – первоначальный уровень воды, тогда после перерезания нити уровень уменшиться на (h). Значит гидростатическое давление до перерезания нити [P_1=rho g H] но так как есть еще сила натяжения нити, которая удерживает шар в воде, но не действует на дно, то сила давления на дно равна [F_1=rho cdot g cdot H cdot S -T] Во втором случае нить обрывается и шар всплывает и уровень уменьшается на (h), тогда сила давления на дно будет равна [F_2=rho cdot g cdot (H-h)cdot S] Поскольку масса щара и воды остается неизменным, то и сила давления на дно при равновесных состояниях остается неизменной, а значит мы можем приравнять (F_1) и (F_2) [rho cdot g cdot H cdot S -T=rho cdot gcdot H cdot S -rho cdot gcdot h cdot S] Выразим силу натяжения нити [T=rho cdot gcdot h cdot S=1000 text{ кг/м$^3$}cdot 10text{ Н/кг} cdot 0,05text{ м}cdot 0,01text{ м$^2$}=5text{ Н}]
Ответ: 5
Невесомый стержень АВ с двумя малыми грузиками массами (m_1 = 200) г и (m_2 = 100) г, расположенными в точках (C) и (B) соответственно, шарнирно закреплён в точке (A). Груз массой (M = 100) г подвешен к невесомому блоку за невесомую и нерастяжимую нить, другой конец которой соединён с нижним концом стержня, как показано на рисунке. Вся система находится в равновесии, если стержень отклонён от вертикали на угол (alpha=30^circ), а нить составляет угол с вертикалью, равный (beta =30^circ). Расстояние (АС = b =) 25 см. Определите длину (l) стержня (АВ). Сделайте рисунок с указанием сил, действующих на груз (M) и стержень.

“Демоверсия 2021”
Сделаем рисунок с указанием всех сил 
Запишим правило моментов относительно точки А. В точке (B) действует только сила натяжения нити равная силе тяжести (m_1g), в точке (C) действует вниз сила натяжения нити равная силе тяжести (m_2g) и сила натяжения нити, действующая вверх, равная (Mg) [m_1g sin alpha cdot b+ m_2g sin alpha cdot l = Mgsin (180-alpha-beta)cdot l] Откуда (l) [l=dfrac{m_1g sin alpha cdot b}{Mgsin (alpha+beta)-m_2g sin alpha cdot AC}=dfrac{0,2 text{ кг}cdot sin 30^circcdot 25text{ см}}{0,2text{ кг}cdot sin 60^circ-0,2text{ кг}cdot sin 30^circ}approx 68,3text{ см}]
Ответ: 68,3
В сосуд с привязанным нитью ко дну деревянным шариком наливают воду так, что шарик частично погружается под воду, а нить натягивается и действует на шарик с силой (T = 7) H. На сколько изменится уровень воды в сосуде после перерезания нити? Площадь дна сосуда (S=100) см(^2).
“Досрочная волна 2019 вариант 2”
Поскольку масса воды и шарика неизменна, то сила давления на дно сосуда одинакова в двух случаях: [rho g h_1S -T =rho g h_2S Rightarrow rho g S Delta h =T Rightarrow Delta h=dfrac{T}{rho g S}=dfrac{7text{ Н}}{1000text{ кг/м$^3$}cdot 10text{ Н/кг}cdot 10^{-2}text{ м$^2$} }=0,07text{ м}]
Ответ: 0,07
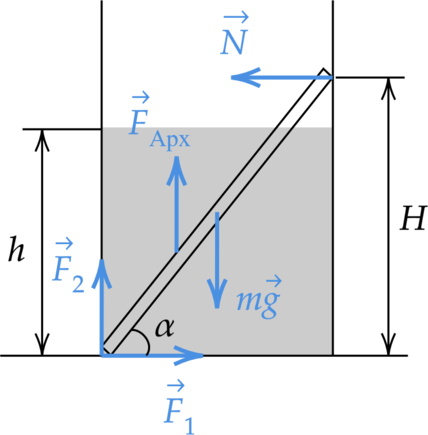
Гладкий цилиндр лежит между двумя плоскостями, одна из которых вертикальна, а линия их пересечения горизонтальна (см. рисунок). Сила давления цилиндра на вертикальную стенку в (n=sqrt{3}) раза превышает силу тяжести, действующую на цилиндр. Найдите угол (alpha) между плоскостями. Сделайте рисунок, на котором укажите силы, действующие на цилиндр.

“Досрочная волна 2020 вариант 1”
Сделаем рисунок 
По третьем закону Ньютона, на вертикальную стенку действует цилиндр с силой (sqrt{3}mg), а значит стенка действует с такой же силой на цилиндр Запишем второй закон Ньютона, с учетом покоя тела [vec{N_1}+vec{N_2}+vec{mg}=0] Найдем тангенс угла (alpha) [tg alpha =dfrac{mg}{N_2}= dfrac{mg}{mgsqrt{3}}=dfrac{1}{sqrt{3}}] А значит угол равен (30^circ)
Ответ: 30
В гладкий высокий стакан радиусом 4 см поставили однородную алюминиевую палочку длиной 10 см и массой 0,9 г, после чего в стакан налили до высоты h = 4 см воду. Найдите модуль силы (F), с которой верхний конец палочки давит на стенку стакана. Сделайте рисунок с указанием сил, действующих на палочку. Ответ дайте в мН.

1. Найдем высоту палочки, относительно дна стакана [H=sqrt{l^2-4R^2}=sqrt{0,01text{ м$^2$}-4cdot 0,0016text{ м$^2$}}=0,06text{ м}] где (l) – длина палочки, (R) – радиус стакана.
2. Сделаем рисунок с изображением всех сил, действующих на палочку.  3. Найдем силу Архимеда, действующую на палочку. Палочка погружена в жидкость на (dfrac{h}{H}) от своего объема, то есть [F_text{ Арх}=rho_text{ж}gleft(dfrac{h}{H}V right)=dfrac{rho_text{ж}}{rho}dfrac{mgh}{H }] где (V) – объем тела, (rho) – плотность палочки, (rho_text{ж}) – плотность жидкости.
3. Найдем силу Архимеда, действующую на палочку. Палочка погружена в жидкость на (dfrac{h}{H}) от своего объема, то есть [F_text{ Арх}=rho_text{ж}gleft(dfrac{h}{H}V right)=dfrac{rho_text{ж}}{rho}dfrac{mgh}{H }] где (V) – объем тела, (rho) – плотность палочки, (rho_text{ж}) – плотность жидкости.
4. Запишем правило моментов, относительно оси, проходящей перпендикулярно рисунку через точку приложения сил (F_2) и (F_1). [mgdfrac{l}{2} cos alpha -F_text{арх}left(dfrac{l}{4}cos alpha right)-Nlsin alpha =0] Преобразуем [mgR-F_text{арх}left(dfrac{h}{2}ctg alpharight)-NH=0] Выразим силу реакции опоры. С учетом третьего закона Ньютона она будет равна силе давления палки на стенку сосуда. [N=mgdfrac{R}{H}-F_text{арх}left(dfrac{h}{2H}ctg alpharight)=mgdfrac{R}{H}left( 1-dfrac{rho_text{ж}}{rho}left(dfrac{h}{H}right)^2right)=] [F=N=0,0009text{ кг}cdot 10text{ Н/кг}dfrac{0,04text{ м}}{0,06text{ м}}left( 1-dfrac{1000text{ кг/м$3$}}{2700text{ кг/м$3$}}left( dfrac{0,04text{ м}}{0,06text{ м}}right)^2 right)approx 5cdot 10^{-3}text{ Н}]
Ответ: 5
Источник

Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 1448
Из крана выливается вода. Начиная с некоторого места диаметр струи уменьшается на протяжении $h$ от $b$ до $c$.
Сколько воды вытечет из крана за время $t$?
Подробнее
Задача по физике – 1449
Из широкого сосуда через узкую цилиндрическую трубку вытекает жидкость плотности $rho$. Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха $P_{0}$.
Подробнее
Задача по физике – 1450
Сосуд с водой подвешен к потолку. Высота воды в сосуде $H$. На сколько изменится натяжение веревки, если в днище сосуда открыть маленькое отверстие сечения $S$, из которого вытекает вода?
Подробнее
Задача по физике – 1451
Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда $S_{1}$, сечение струи $S_{2}$. Уровень воды в сосуде перемещается с постоянным ускорением. Найдите это ускорение.
Подробнее
Задача по физике – 1452
Насос должен подавать ежесекундно объем воды $Q$ на высоту $H$ по трубе постоянного сечения $S$. Какова должна быть мощность насоса? КПД насоса $eta$, плотность воды $rho$.
Подробнее
Задача по физике – 1453
По трубе сечением $S$, изогнутой под прямым углом, течет вода со скоростью $v$. Плотность воды $rho$.
Чему равна сила бокового давления в месте закругления трубы?
Подробнее
Задача по физике – 1821
Как вы думаете, справедлив ли закон сообщающихся Сосудов (однородная жидкость в сообщающихся сосудах имеет один и тот же уровень), если в одном из сосудов на поверхности жидкости находится некоторый поплавок (капиллярность не учитывать)?
Подробнее
Задача по физике – 1822
Достаточно длинная открытая снизу трубка с плотно пригнанным поршнем, который может все же двигаться по трубке без трения, находится под водой и удерживается с помощью веревки (рис.). Верхний конец трубки над поршнем пустой. Как зависит сила натяжения веревки от глубины погружения трубки в воду?

Подробнее
Задача по физике – 1823
Ведро, имеющее массу $m$, вместимость $V$, вытаскивают с водой из колодца. Плотность материала, из которого сделано ведро, равна $rho$, плотность воды $rho_{в}$. Какую силу необходимо приложить для подъема этого ведра, пока оно находится под водой и когда его вытащили из воды? Сопротивление воды движению ведра не учитывать.
Подробнее
Задача по физике – 1824
Для того чтобы поднять уровень жидкости в сосуде на Высоту $h$ с помощью насоса, надо совершить некоторую работу. Изменится ли необходимая для этой же цели работа, если на поверхности жидкости плавает какое-нибудь тело?
Подробнее
Задача по физике – 1825
Изменится ли осадка парохода, перешедшего из северных вод в экваториальные, вследствие изменения ускорения свободного падения с широтой?
Подробнее
Задача по физике – 1826
Как зависит подъемная сила аэростата от температуры, при которой производится его подъем?
Подробнее
Задача по физике – 1827
Когда объясняют опыт со взвешиванием воздуха, [иногда говорят, что сначала взвешивают колбу с воздухом, а затем, после откачки воздуха из колбы, взвешивают одну колбу. Разность показаний весов в первом и втором случаях и составляет массу воздуха в объеме колбы. Правильно ли такое толкование опыта по взвешиванию воздуха?
Подробнее
Задача по физике – 1828
Можно ли измерить плотность воздуха, взвешивая мягкий воздухонепроницаемый мешок сначала пустой (сжатый), а потом наполненный воздухом? Объем мешка в наполненном Состоянии известен.
Подробнее
Источник
Статьи
Среднее общее образование
Физика
Предлагаем вашему вниманию разбор 29 задания ЕГЭ-2018 по физике. Мы подготовили пояснения и подробный алгоритм решения, а также рекомендации по использованию справочников и пособий, которые могут понадобиться при подготовке к ЕГЭ.
20 марта 2018
Задание 29
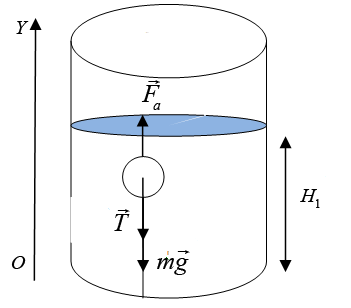
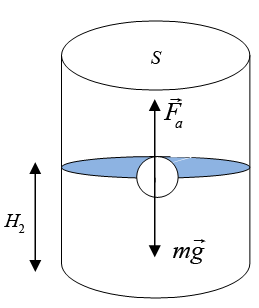
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h = 5 см. Найдите силу натяжения нити T.
Решение
| |
Рис. 1 | Рис. 2 |
Первоначально деревянный шар привязан нитью ко дну цилиндрического сосуда площадью дна S = 100 см2 = 0,01 м2 и полностью погружен в воду. На шар действуют три силы: сила тяжести со стороны Земли, – сила Архимеда со стороны жидкости, – сила натяжения нити, результат взаимодействия шара и нити. По условию равновесия шара в первом случае геометрическая сумма всех действующих на шарик сил, должна быть равна нулю:
ЕГЭ-2018. Физика. Сдаем без проблем!
В книге содержатся материалы для успешной сдачи ЕГЭ по физике: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, решение задач повышенного уровня сложности, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену. Издание содержит задания разных типов по всем темам, проверяемым на ЕГЭ по физике, а также решение задач повышенного уровня сложности.
Купить
Выберем координатную ось OY и направим ее вверх. Тогда с учетом проекции уравнение (1) запишем:
Fa1 = T + mg (2).
Распишем силу Архимеда:
Fa1 = ρ · V1g (3),
где V1 – объем части шара погруженной в воду, в первом это объем всего шара, m – масса шара , ρ – плотность воды. Условие равновесия во втором случае
Fa2 = mg (4)
Распишем силу Архимеда в этом случае:
Fa2 = ρ · V2g (5),
где V2 – объем части шара, погруженной в жидкость во втором случае.
Поработаем с уравнениями (2) и (4) . Можно использовать метод подстановки или вычесть из (2) – (4), тогда Fa1 – Fa2 = T, используя формулы (3) и (5) получим ρ · V1g – ρ · V2g = T;
ρg (V1 – V2) = T (6)
Учитывая, что
V1 – V2 = S ·h (7),
где h = H1 – H2; получим
T = ρ · g · S · h (8)
Подставим числовые значения
| T = 1000 | кг | · 10 | м | · 5 · 10–2 м = 5 Н |
| м3 | с2 |
Ответ: 5 Н.

ЕГЭ-2018. Физика. 30 тренировочных вариантов экзаменационных работ
Издание содержит:
• 30 тренировочных вариантов ЕГЭ
• инструкцию по выполнению и критерии оценивания
• ответы ко всем заданиям
Тренировочные варианты помогут учителю организовать подготовку к ЕГЭ, а учащимся – самостоятельно проверить свои знания и готовность к сдаче выпускного экзамена.
Купить
Источник
Комбинированные задачи по механике
Особенность задания № 29 заключается в том, что в нем требуется использование материалов не менее чем из двух-трех разделов механики. Актуальные сведения, необходимые для решения задания, приведены в разделе теории. Законы сохранения, силы, действующие в макромире, и другая нужная информация содержится в разделах теории соответствующих типовых заданий по механике.
Теория к заданию №29 ЕГЭ по физике
Проекции сил, скорости, ускорения
При решении расчетных задач векторные величины требуется представлять в их скалярных (числовых) значениях. Для этого их выражают в виде проекций на оси выбранной инерционной с-мы координат, например: Fx, vY. Система координат может быть представлена единственной осью (Ox или Oy), если речь идет о движении по горизонтальной плоскости, о свободном падении тела и т.п. При перемещении тела под углом к горизонту и в других более или менее сложных случаях требуется прямоугольная система (Oxy).
Если направление вектора физ.величины совпадает с направлением координатной оси (или одной из осей, когда задача решается в рамках прямоугольной с-мы координат), то величина проекции совпадает с величиной ее модуля. К примеру, если тело бросают вертикально вниз с ускорением
, то представив схему движения в системе Ox, ось которой направлена тоже вертикально вниз, получим для расчетов: .
Если векторная величина направлена по отношению к осям под углом, то вектор вместе со своими проекциями на оси прямоугольной системы координат образует прямоугольный треугольник, в котором вектор – гипотенуза, а проекции – катеты. Приняв угол между вектором и осью Оx равным α (на рисунке представлен пример для вектора ускорения),
величины проекций определяют таким образом:
;
.
Закон Архимеда
На помещенное в жидкость тело действует выталкивающая его сила. Эта сила традиционно обозначается как FA и вычисляется по формуле:
,
где ρ – плотность жидкости, в которую помещено тело,
– ускорение свободного падения, V – объем погруженного тела. Относительно объема нужно отметить важный момент: если тело погружено полностью, то для расчета должен браться полный его объем; если тело погружено частично, то следует использовать объем части тела, находящейся в толще жидкости.
Разбор типовых вариантов №29 по физике
Демонстрационный вариант 2018
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S=100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой Т. Если нить перерезать, то шар всплывет, а уровень воды изменится на h=5 см. Найдите силу натяжения нити Т.
Алгоритм решения:
- Переводим числовые данные, приведенные в условии, в СИ. Записываем необходимое для решения табличное значение для плотности жидкости (воды).
- Анализируем начальную ситуацию (шар на нити). Определяем силы, действующие на шар.
- Анализируем ситуацию после перерезания нити. Определяем силы, действующие на шар. Составляем уравнение для вычисления объема вытесненной части шара.
- Применяя 3-й з-н Ньютона, составляем уравнения силы для начальной ситуации (1) и последующей (2). Из этой системы выражаем Т. Используя формулу з-на Архимеда и выражение для объема вытесненной части шара, находим Т.
- Записываем ответ.
Решение:
1. Переведем S и h в СИ: , . Плотность воды ρ равна:. 2. Поскольку шар полностью погружен в воду, то он вытесняет объем воду, равный собственному объему. Обозначим его V1. На погруженный шар действуют: сила тяжести mg, сила Архимеда FA1, сила натяжения Т.
3. После перерезания нити уровень воды в сосуде понизился, поскольку шар всплыл и теперь занимает в толще воды только часть своего объема, вытесняя меньше воды. Обозначим этот объем через V2. Объем части шара, оказавшегося над поверхностью воды, составляет
. Силы, действующие на шар: сила тяжести mg, сила Архимеда FT2.
4. В обеих ситуациях шар находится в равновесии. Поэтому по 3-му з-у Ньютона:
(1) – (2) :
.
Отсюда:
.
Ответ: 5 Н.
Первый вариант (Демидова, № 5)
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 100 г и m2 = 400 г, связанные нерастяжимой невесомой нитью длиной l. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). При вращении штанги с частотой 900 об/мин модуль силы натяжения нити, соединяющей грузы, T = 150 Н. Определите длину нити l.
Алгоритм решения:
- Определяем для каждого из грузов инерциальную с-му отсчета, в которой, применив 2-й з-н Ньютона, записываем уравнения в соответствующих проекциях.
- Определяем вид ускорения и записываем формулы для его вычисления. Из предыдущих формул формируем уравнения для определения сил, действующих на грузы.
- Анализируем соотношения между входящими в уравнения величинами и после преобразований выводим формулу для вычисления искомой длины.
- Переводим в СИ несоответствующие ей значения из условия. Подставляем данные в результирующее уравнение, вычисляем длину нити.
- Записываем ответ.
Решение:
1. Выбираем системы отсчета для каждого из грузов так, чтобы их оси были направлены горизонтально (вдоль штанги) от края штанги к оси вращения:
Т1 и Т2 на рисунке – силы, действующие соответственно на левый и правый грузы.
На основании 2-го з-на Ньютона запишем уравнения силы в проекции на оси с-м отсчета:
;
.
2. Т.к. в данном случае имеет место вращательное движение, то грузы испытывают центростремительное ускорение. Для их вычисления используем формулу:
, где w – угловая скорость их вращательного движения, R – радиусы окружностей их вращения. Поскольку , то применив эту и предыдущую формулы для каждого груза, получим: , . Подставим формулы для и в (1) и (2). Получим:
;
.
3. Если l – длина нити между грузами, то
. Выразим радиус вращения одного из грузов (например, правого) через радиус другого: .Поскольку грузы связаны в единую систему, то . Отсюда: (3)=(4) → . Учтя при этом (5), имеем: (6).
Приравняем Т к одной из сил, например:
. Приняв при этом во внимание (6), получаем: . Тогда: .
4. Переводим данные из условия в СИ:
; ; . Найдем l:
Ответ: 0,21 м.
Второй вариант (Демидова, № 11)
Алгоритм решения:
- На основании условия чертим схему движения описанных объектов.
- Используя з-н сохранения импульса, записываем уравнение для импульсов снаряда и осколков в проекции на ось Ох. Из него выразим модуль скорости для 2-го осколка (1).
- Приняв во внимание, что кинет.энергия осколков (по условию) увеличилась на ∆Е, запишем уравнение, описывающее соотношение энергий снаряда и осколков. Отсюда выразим массу осколка (2).
- Подставив (1) в (2) получим результирующее выражение для массы m.
- Записываем ответ.
Решение:
1. Схема движения снаряд и его осколков выглядит так:
На схеме масса снаряда обозначена как 2m. Это следует из условия, что снаряд разорвался на равные части. Поскольку масса каждого из них составляет m, то их суммарная масса, являющаяся массой неразорвавшегося заряда, как раз и равна 2m. Обозначение на схеме «
» – это скорость второго осколка, движущегося в противоположную снаряду сторону. Обозначения вида mv – импульсы, соответствующие снаряду и паре осколков.
2. По з-ну сохранения импульса в момент разрыва снаряда
. Отсюда: .
3. Выразим взаимосвязь энергий до и после разрыва снаряда:
. Выполним преобразования и выразим m:
4. (1) → (2) :
.
Ответ:
.
Даниил Романович | ???? Скачать PDF |
Источник