Сосуд с водой подвешенный на веревке длиной

#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник

Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 1448
Из крана выливается вода. Начиная с некоторого места диаметр струи уменьшается на протяжении $h$ от $b$ до $c$.
Сколько воды вытечет из крана за время $t$?
Подробнее
Задача по физике – 1449
Из широкого сосуда через узкую цилиндрическую трубку вытекает жидкость плотности $rho$. Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха $P_{0}$.
Подробнее
Задача по физике – 1450
Сосуд с водой подвешен к потолку. Высота воды в сосуде $H$. На сколько изменится натяжение веревки, если в днище сосуда открыть маленькое отверстие сечения $S$, из которого вытекает вода?
Подробнее
Задача по физике – 1451
Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда $S_{1}$, сечение струи $S_{2}$. Уровень воды в сосуде перемещается с постоянным ускорением. Найдите это ускорение.
Подробнее
Задача по физике – 1452
Насос должен подавать ежесекундно объем воды $Q$ на высоту $H$ по трубе постоянного сечения $S$. Какова должна быть мощность насоса? КПД насоса $eta$, плотность воды $rho$.
Подробнее
Задача по физике – 1453
По трубе сечением $S$, изогнутой под прямым углом, течет вода со скоростью $v$. Плотность воды $rho$.
Чему равна сила бокового давления в месте закругления трубы?
Подробнее
Задача по физике – 1821
Как вы думаете, справедлив ли закон сообщающихся Сосудов (однородная жидкость в сообщающихся сосудах имеет один и тот же уровень), если в одном из сосудов на поверхности жидкости находится некоторый поплавок (капиллярность не учитывать)?
Подробнее
Задача по физике – 1822
Достаточно длинная открытая снизу трубка с плотно пригнанным поршнем, который может все же двигаться по трубке без трения, находится под водой и удерживается с помощью веревки (рис.). Верхний конец трубки над поршнем пустой. Как зависит сила натяжения веревки от глубины погружения трубки в воду?

Подробнее
Задача по физике – 1823
Ведро, имеющее массу $m$, вместимость $V$, вытаскивают с водой из колодца. Плотность материала, из которого сделано ведро, равна $rho$, плотность воды $rho_{в}$. Какую силу необходимо приложить для подъема этого ведра, пока оно находится под водой и когда его вытащили из воды? Сопротивление воды движению ведра не учитывать.
Подробнее
Задача по физике – 1824
Для того чтобы поднять уровень жидкости в сосуде на Высоту $h$ с помощью насоса, надо совершить некоторую работу. Изменится ли необходимая для этой же цели работа, если на поверхности жидкости плавает какое-нибудь тело?
Подробнее
Задача по физике – 1825
Изменится ли осадка парохода, перешедшего из северных вод в экваториальные, вследствие изменения ускорения свободного падения с широтой?
Подробнее
Задача по физике – 1826
Как зависит подъемная сила аэростата от температуры, при которой производится его подъем?
Подробнее
Задача по физике – 1827
Когда объясняют опыт со взвешиванием воздуха, [иногда говорят, что сначала взвешивают колбу с воздухом, а затем, после откачки воздуха из колбы, взвешивают одну колбу. Разность показаний весов в первом и втором случаях и составляет массу воздуха в объеме колбы. Правильно ли такое толкование опыта по взвешиванию воздуха?
Подробнее
Задача по физике – 1828
Можно ли измерить плотность воздуха, взвешивая мягкий воздухонепроницаемый мешок сначала пустой (сжатый), а потом наполненный воздухом? Объем мешка в наполненном Состоянии известен.
Подробнее
Источник
29. Механика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вертикальная труба с поршнем, плотно прилегающим к ее внутренним стенкам, опущена нижним концом в воду. Вначале поршень находился в самом нижнем положении, на уровне воды, а затем его медленно поднимают на высоту 20 м. Пренебрегая трением, найдите совершенную при этом работу (в кДж). Площадь поршня 100 см(^2). Атмосферное давление 100 кПа.
Процесс поднятия поршня происходит в 2 этапа. Первый этап: давление под поршнем будет положительным и равное [p_0-rho g h] где (rho) – плотность воды, (h) – высота подъеда поршня.
Вода будет заполнять весь объем под поршнем, а приложенная к поршню сила будет компенсировать давление внутри, она будет равна [F=rho g h S] Она будет линейно возрастать. Это будет до момента, пока вода не поднимется на высоту, равную [h_0=dfrac{p_0}{rho g}=dfrac{100text{ кПа}}{1000text{ кг/м$^3$ cdot 10 Н/кг}}=10text{ м}] При подъеме поршня на высоту (h_0) давление станет равным нулю. После этого вода перестает подниматься, а сила, приложенная к поршню, остается равной [F’=rho g h_0 S=p_0S] Работа по поднятию равна сумме работ: работе по поднятию до высоты (h_0) (A_0=dfrac{0+F_1}{2}h_0=dfrac{p_o S h_0}{2}) (так как она линейно возрастает, то берем как среднее арифметическое от начального, до конечного) и работе по поднятию от высоты (h_0) и конечной высоты (A_1=F_1(h_1-h_0)=p_o Sh_1-p_o Sh_0). Значит полная работа равна [A=dfrac{p_o S h_0}{2}+ p_0 S h_1 -p_0 Sh_0=p_0 S (h_1 -dfrac{h_0}{2})=100text{ кПа}cdot 10^{-2}text{ м$^2$}(20text{ м}-5text{ м})=15text{ кДж}]
Ответ: 15
Шар, до половины погруженный в воду, лежит на дне сосуда и оказывает на него давление с силой, равной 1/3 действующей на него силы тяжести. Найти плотность материала шара.
Сила давления на дно будет равна разности силы тяжести и силы Архимеда, действующих на шар [N=m g-rho_{0} g frac{V}{2},] где (N) – сила давления на дно, (m) – масса шарика,(rho_0) – плотность воды, (V) – объем шарика [N=frac{1}{3} m g] Масса шарика же равна [m=rho V,] где (rho) – плотность материала, из которого сделан шар. Подставим (2) и (3) в (1) и получим [frac{1}{3} rho g V=rho g V-rho_{0} g frac{V}{2}] Откуда плотность тела [rho=frac{3}{4} rho_{0}=frac{3}{4} 1000 text{ кг/м$^3$}=750 text{ кг/м$^3$}]
Ответ: 750
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см(^2). В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой (T). Если нить перерезать, то шар всплывёт, а уровень воды изменится на (h) = 5 см. Найдите силу натяжения нити (T).
“Демоверсия 2018”
Пусть (rho) – плотность жидкости, (H) – первоначальный уровень воды, тогда после перерезания нити уровень уменшиться на (h). Значит гидростатическое давление до перерезания нити [P_1=rho g H] но так как есть еще сила натяжения нити, которая удерживает шар в воде, но не действует на дно, то сила давления на дно равна [F_1=rho cdot g cdot H cdot S -T] Во втором случае нить обрывается и шар всплывает и уровень уменьшается на (h), тогда сила давления на дно будет равна [F_2=rho cdot g cdot (H-h)cdot S] Поскольку масса щара и воды остается неизменным, то и сила давления на дно при равновесных состояниях остается неизменной, а значит мы можем приравнять (F_1) и (F_2) [rho cdot g cdot H cdot S -T=rho cdot gcdot H cdot S -rho cdot gcdot h cdot S] Выразим силу натяжения нити [T=rho cdot gcdot h cdot S=1000 text{ кг/м$^3$}cdot 10text{ Н/кг} cdot 0,05text{ м}cdot 0,01text{ м$^2$}=5text{ Н}]
Ответ: 5
Невесомый стержень АВ с двумя малыми грузиками массами (m_1 = 200) г и (m_2 = 100) г, расположенными в точках (C) и (B) соответственно, шарнирно закреплён в точке (A). Груз массой (M = 100) г подвешен к невесомому блоку за невесомую и нерастяжимую нить, другой конец которой соединён с нижним концом стержня, как показано на рисунке. Вся система находится в равновесии, если стержень отклонён от вертикали на угол (alpha=30^circ), а нить составляет угол с вертикалью, равный (beta =30^circ). Расстояние (АС = b =) 25 см. Определите длину (l) стержня (АВ). Сделайте рисунок с указанием сил, действующих на груз (M) и стержень.

“Демоверсия 2021”
Сделаем рисунок с указанием всех сил 
Запишим правило моментов относительно точки А. В точке (B) действует только сила натяжения нити равная силе тяжести (m_1g), в точке (C) действует вниз сила натяжения нити равная силе тяжести (m_2g) и сила натяжения нити, действующая вверх, равная (Mg) [m_1g sin alpha cdot b+ m_2g sin alpha cdot l = Mgsin (180-alpha-beta)cdot l] Откуда (l) [l=dfrac{m_1g sin alpha cdot b}{Mgsin (alpha+beta)-m_2g sin alpha cdot AC}=dfrac{0,2 text{ кг}cdot sin 30^circcdot 25text{ см}}{0,2text{ кг}cdot sin 60^circ-0,2text{ кг}cdot sin 30^circ}approx 68,3text{ см}]
Ответ: 68,3
В сосуд с привязанным нитью ко дну деревянным шариком наливают воду так, что шарик частично погружается под воду, а нить натягивается и действует на шарик с силой (T = 7) H. На сколько изменится уровень воды в сосуде после перерезания нити? Площадь дна сосуда (S=100) см(^2).
“Досрочная волна 2019 вариант 2”
Поскольку масса воды и шарика неизменна, то сила давления на дно сосуда одинакова в двух случаях: [rho g h_1S -T =rho g h_2S Rightarrow rho g S Delta h =T Rightarrow Delta h=dfrac{T}{rho g S}=dfrac{7text{ Н}}{1000text{ кг/м$^3$}cdot 10text{ Н/кг}cdot 10^{-2}text{ м$^2$} }=0,07text{ м}]
Ответ: 0,07
Гладкий цилиндр лежит между двумя плоскостями, одна из которых вертикальна, а линия их пересечения горизонтальна (см. рисунок). Сила давления цилиндра на вертикальную стенку в (n=sqrt{3}) раза превышает силу тяжести, действующую на цилиндр. Найдите угол (alpha) между плоскостями. Сделайте рисунок, на котором укажите силы, действующие на цилиндр.

“Досрочная волна 2020 вариант 1”
Сделаем рисунок 
По третьем закону Ньютона, на вертикальную стенку действует цилиндр с силой (sqrt{3}mg), а значит стенка действует с такой же силой на цилиндр Запишем второй закон Ньютона, с учетом покоя тела [vec{N_1}+vec{N_2}+vec{mg}=0] Найдем тангенс угла (alpha) [tg alpha =dfrac{mg}{N_2}= dfrac{mg}{mgsqrt{3}}=dfrac{1}{sqrt{3}}] А значит угол равен (30^circ)
Ответ: 30
В гладкий высокий стакан радиусом 4 см поставили однородную алюминиевую палочку длиной 10 см и массой 0,9 г, после чего в стакан налили до высоты h = 4 см воду. Найдите модуль силы (F), с которой верхний конец палочки давит на стенку стакана. Сделайте рисунок с указанием сил, действующих на палочку. Ответ дайте в мН.

1. Найдем высоту палочки, относительно дна стакана [H=sqrt{l^2-4R^2}=sqrt{0,01text{ м$^2$}-4cdot 0,0016text{ м$^2$}}=0,06text{ м}] где (l) – длина палочки, (R) – радиус стакана.
2. Сделаем рисунок с изображением всех сил, действующих на палочку. 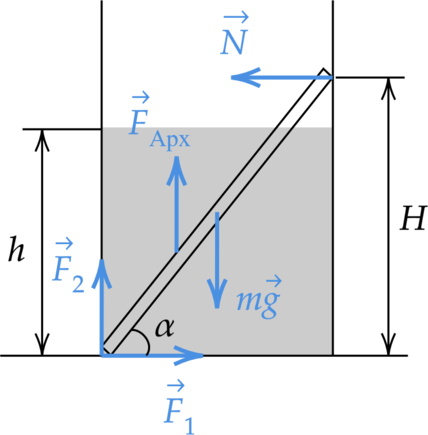 3. Найдем силу Архимеда, действующую на палочку. Палочка погружена в жидкость на (dfrac{h}{H}) от своего объема, то есть [F_text{ Арх}=rho_text{ж}gleft(dfrac{h}{H}V right)=dfrac{rho_text{ж}}{rho}dfrac{mgh}{H }] где (V) – объем тела, (rho) – плотность палочки, (rho_text{ж}) – плотность жидкости.
3. Найдем силу Архимеда, действующую на палочку. Палочка погружена в жидкость на (dfrac{h}{H}) от своего объема, то есть [F_text{ Арх}=rho_text{ж}gleft(dfrac{h}{H}V right)=dfrac{rho_text{ж}}{rho}dfrac{mgh}{H }] где (V) – объем тела, (rho) – плотность палочки, (rho_text{ж}) – плотность жидкости.
4. Запишем правило моментов, относительно оси, проходящей перпендикулярно рисунку через точку приложения сил (F_2) и (F_1). [mgdfrac{l}{2} cos alpha -F_text{арх}left(dfrac{l}{4}cos alpha right)-Nlsin alpha =0] Преобразуем [mgR-F_text{арх}left(dfrac{h}{2}ctg alpharight)-NH=0] Выразим силу реакции опоры. С учетом третьего закона Ньютона она будет равна силе давления палки на стенку сосуда. [N=mgdfrac{R}{H}-F_text{арх}left(dfrac{h}{2H}ctg alpharight)=mgdfrac{R}{H}left( 1-dfrac{rho_text{ж}}{rho}left(dfrac{h}{H}right)^2right)=] [F=N=0,0009text{ кг}cdot 10text{ Н/кг}dfrac{0,04text{ м}}{0,06text{ м}}left( 1-dfrac{1000text{ кг/м$3$}}{2700text{ кг/м$3$}}left( dfrac{0,04text{ м}}{0,06text{ м}}right)^2 right)approx 5cdot 10^{-3}text{ Н}]
Ответ: 5
Источник
