Сосуд с водой скользит по наклонной плоскости
В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).
В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции. Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l) высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.
В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r – радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).
При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в. Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
Проф. С.И.Лежнин, проф. О.Я.Савченко, проф. О.Ю.Цвелодуб,
СУНЦ НГУ, г. Новосибирск
9-й класс
1. Мотоциклист движется со скоростью u навстречу колонне автомобилей. После того как мотоциклист увеличил скорость в два раза, он стал встречать автомобили из колонны в полтора раза чаще. Какова скорость автомобилей в колонне ?
Решение
Пусть расстояние между автомобилями L. Тогда вначале время между встречами мотоциклиста с автомобилями равнялось После удвоения скорости но, по условию задачи, Отсюда = u.
2. Маленький шарик скользит по плоскости, наклонённой под углом к горизонту, которая вплотную примыкает к другой наклонной плоскости. Чему равен угол между горизонтом и второй плоскостью, если известно, что после упругого удара о неё шарик полетел вертикально?
Решение
В отсутствие трения угол падения шарика на вторую плоскость (отсчитываемый от нормали к ней) равен углу отражения. Угол между ветикалью и нормалью ко второй плоскости равен . Из построения видно, что шарик взлетит вертикально, если Отсюда = 45° – /2.
3. Шарик касается дна сосуда и при этом наполовину погружён в воду. После того как долили воды, так что шарик скрылся под водой полностью, сила, с которой он давит на дно сосуда, уменьшилась в 3 раза. Чему равна плотность материала, из которого изготовлен шарик?
Решение
Обозначим силу, с которой шарик вначале давил на дно сосуда, через N, плотность воды в, искомую плотность материала х, объём шарика V. В первом случае объём вытесненной воды равен V/2, а во втором V. В обоих случаях шарик находится в покое, поэтому суммарная сила, действующая на него, равна нулю:
Решая совместно оба уравнения, получим:
Отсюда или
4. Гирлянду из N одинаковых лампочек подсоединяли к источнику напряжения через входной резистор двумя способами: лампочки между собой соединены параллельно, лампочки между собой соединены последовательно. В обоих случаях накал лампочки одинаков. Чему равно сопротивление входного резистора, если сопротивление каждой лампочки R?
Решение
Пусть напряжение на входе цепи в обоих случаях равно U, а сопротивление входного резистора Rх. Поскольку накал лампочки одинаков в обоих случаях, то одинаков и ток через лампочку. Обозначим его Iл. Сопротивление N параллельно соединённых одинаковых лампочек равно R/N, а последовательно соединённых – RN.
В первом случае:
общее сопротивление полный ток
Полный ток разделяется на N токов, текущих через каждую лампочку:
Во втором случае:
Приравняв выражения для Iл, получим:
Отсюда Rx = R.
10-й класс
1. См. задачу 3 для 9-го класса.
2. См. задачу 4 для 9-го класса.
3. Бруску, лежащему на наклонной плоскости, щелчком сообщают горизонтальную скорость . Определите ускорение бруска сразу после щелчка. Угол наклона плоскости к горизонту равен a, коэффициент трения между бруском и плоскостью равен .
Решение
Направим ось x горизонтально, а ось y – вниз вдоль плоскости. Сила реакции плоскости N = mgcos. В первый момент сила трения действует только вдоль оси x, т.к. она направлена против скорости.
Сила трения равна Fx = Fтр = N = mgcos. Сила, действующая вдоль наклонной плоскости, Fy = mgsin.
Горизонтальное ускорение ax = Fx/m = gcos.
Ускорение вдоль плоскости ay = Fy/m = gsin.
Полное ускорение
4. Сила сопротивления воздуха, действующая на тело, пропорциональна квадрату скорости тела относительно воздуха: Fcопр = A2 (постоянная A известна). Тело вначале движется в воздухе под действием внешней постоянной силы с установившейся скоростью 0. С некоего момента времени (t = 0) внешняя сила изменяется так, что тело тормозится с постоянным ускорением a вплоть до остановки. Как зависит от времени внешняя сила F? Масса тела m.
Решение
Запишем 2-й закон Ньютона для тела с учётом того, что ускорение равно -a (ускорение отрицательно) и на тело действуют две силы:
-ma = F(t) – A2 = F(t) – A(0 – at)2.
Отсюда F(t) = A(0 – at)2 – ma.
5. Ракета массой m стартует под углом 30° к горизонту. Найдите ускорение ракеты и силу тяги реактивной струи, которая образует угол 60° с горизонтом. Ускорение свободного падения g. Двигатель установлен так, что ракета не вращается.
Решение
На старте на ракету действуют сила тяги T и сила тяжести mg. Спроецируем силы на направление взлёта и перпендикулярно ему:
Решая эти уравнения, находим:
11-й класс
1. См. задачу 3 для 9-го класса.
2. См. задачу 5 для 10-го класса.
3. Два сообщающихся сосуда площадью сечений S1 и S2 (S1 > S2) и высотой h заполнены жидкостью до уровня h/2. На поверхности жидкости в сосуде сечением S1 лежит невесомый поршень. На поршень начинают осторожно сыпать песок. Определить массу насыпанного песка, при которой жидкость начнёт выливаться из сосуда сечением S2. Плотность жидкости , ускорение свободного падения g.
Решение
Так как поршень невесомый, в любой момент силы, действующие на него, находятся в равновесии. Это сила давления со стороны жидкости pS1 и сила реакции со стороны песка, Она, в свою очередь, равна силе тяжести песка, т.к. песок насыпают медленно. В момент, когда вода начнёт выливаться, в правом сосуде высота столба будет равна h, а в левом x. Поэтому давление на поршень со стороны жидкости будет равно p = g(h – x). Так как в правый сосуд дополнительная вода перешла из левого, то
Из условия равновесия поршня Mg = g(h – x)S1. В результате искомая масса насыпанного песка
4. Вертикально стоящий герметичный сосуд с газом разделён тонким подвижным массивным поршнем на две одинаковые части. Вначале в верхней части температура была равна T1, давление р, а в нижней T2 и 2р соответственно. После того как температура в обеих частях сравнялась с температурой окружающей атмосферы Tx, поршень остался на месте. Определите Tх.
Решение
Так как масса газа в каждой части остаётся неизменной, то имеем:
где р1 и р2 – конечные давления в верхней и нижней частях соответственно.
Из условия равновесия поршня (обозначим его массу M) получаем связь между давлениями в обеих частях сосуда:
Отсюда следует, что р1 + р = р2.
В результате для значения температуры окружающего воздуха получаем
5. Горизонтальная плоскость делит пространство на две части: область с однородным электрическим полем E и область, в которой электрического поля нет. На каком расстоянии h от плоскости был отпущен шарик массой m и зарядом q, если он, пролетев сквозь небольшое отверстие в плоскости, возвратился на прежнее место через время ? Ускорение свободного падения g, qE > mg.
Решение
Вначале шарик движется с ускорением g, пока не достигнет плоскости с максимальной скоростью . Время этого равноускоренного движения Далее шарик тормозится с ускорением до остановки в течение времени
Полное время движения равно
Находя из этого уравнения скорость и подставляя её в равенство для равноускоренного движения 2 = 2gh, получим:
Запросы следует направлять директору заочной школы СУНЦ НГУ Кутузовой Ольге Ивановне (kutuzova@sscadm.nsu.ru).
Источник
Задача 9. На плоскости, тангенс угла наклона которой равен коэффициенту трения, лежит монета. В горизонтальном направлении вдоль плоскости монете сообщили скорость v. Найдите установившуюся скорость монеты.
Эта задача со звездочкой, значит трудная (олимпиадная). Сделаем рисунок)
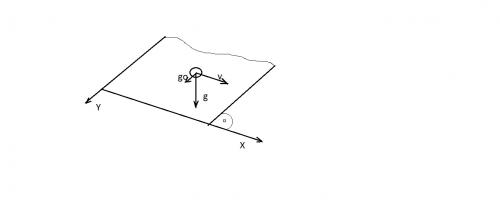
На этом рисунке g направлено вертикально вниз, вектор скорости V вдоль плоскости горизоньально, а вектор g0 это составляющая вектора g на плоскость (g0 = g sin α ). Выберем оси Х и Y.После некоторого времени движение будет установившемся. Запишем уравнения движения по осям.
may = mg sin α – μmg cos α
max = μmg cos α. Откуда ay = g sin α – μg cos α; ax = μg cos α. Проекции скоростей имеют вид
vy = gt sin α – μgt cos α; vx = v – μgt cos α. Сделаем два замечания: условие равновесия монеты в исходном состоянии имеет вид μmg cos α = mg sin α, значит μ = tg α. Это условие означает, что ускорение вдоль оси Y отсутствует, а vx примет вид vx = v – gt sin α. Но формально второе выражение есть vy без начальной скорости. Получим: vx = v – vy или (обозначив u = vx = vy установившуюся скорость), получим u = v / 2. Это ответ. Решение слабое, может, и неверное. Но хотя бы один балл может быть заработан.
Задача 9. Тело, находящееся на горизонтальной плоскости, тянут за нить в горизонтальном направлении. Нарисуйте график зависимости силы трения, действующей на тело со стороны плоскости, от силы натяжения нити. Первоначально тело неподвижно. Масса тела 10 кг, коэффициент трения 0,51
Сделаем рисунок и расставим силы.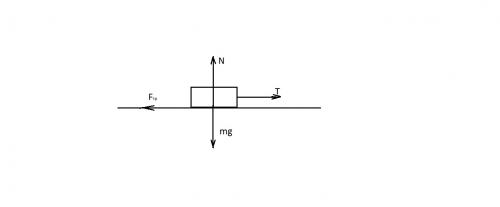 
Сила трения покоя равна Т, чем больше Т, тем больше сила трения. Сила трения будет расти до Fтр макс= μN = =μmg. Запишем второй закона Ньютона
0 = T – Fтр, откуда Fтр = Т. Когда начнется
скольжение, Fтр = Fтр макс = const. График будет выглядеть следующим образом:
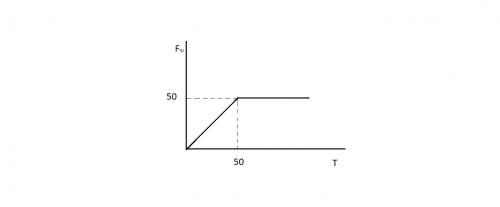
Эта задача уровня В, или даже А
Задача 10. К свободному концу нити, прикрепленной к стенке и переброшенной через ролик, подвешен груз. Ролик закреплен на бруске массы m0, который может скользить по горизонтальной плоскости без трения. В начальный момент нить с грузом отклоняют от вертикали на угол α и затем отпускают. Определите ускорение бруска, если угол, образованный нитью с вертикалью, не меняется при движении системы
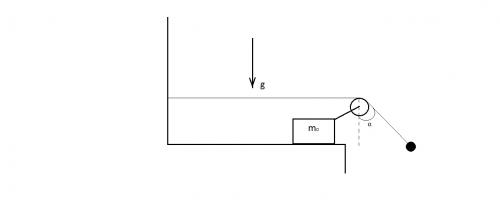
Задача со звездочкой. Сделаем рисунок и расставим силы. Сразу же заметим, что отклонив грузик колебаний не происходит. Почему? Предположим, что система движется влево с ускорением. Тогда грузик действительно останется в покое в отклоненном состоянии. Видимо, это важное предположение.
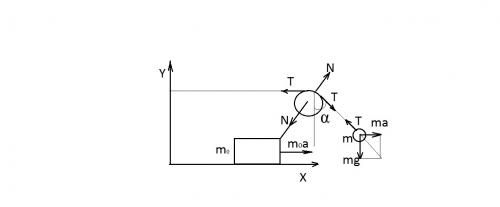
Сила Т – сила натяжения нити, N – сила реакции опоры блока и сила со стороны блока на тело mo. Эти силы обусловлены невесомостью блока и нити, а также нерастяжимости нити. Силы m0a и ma – силы инерции, сила mg – сила тяжести. Тело m0 в покое, т.к. сила инерции m0 компенсируется силой N, котороя, в свою очередь, равна сумме N = T + T (это векторы). Ускорение системы найдем по формуле
tg α = ma / mg, откуда a = g tg α. Это первый ответ. Спроецируем на горизонтальное направление уравнение движения. В движущейся неинерциальной системе тело mo в покое, значит
0 = m0a – T + Tsin α. Подставим значение ускорения и силы Т = mg /cos α получим m0ag·tg α = mg(1 / cos α – tg α) , из которого найдем массу m = m0 sin α /(1 – sin α). Это второй ответ, который, к сожалению не совпал с приведенным в задачнике (m = m0 sin α /(1 – sin α)2 ). Попробуйте найти ошибку или дать другое решение, а меня извините, если я неправильно привел ответ.
Задача 11. Две заряженные частицы массы m и 2m, равные по модулю импульсы, одновременно вылетают навстречу друг другу из точек А и В. Частицы взаимодействуют только друг с другом. По траектории частицы массы 2m, приведенной на рисунке, восстановите траекторию другой частицы.
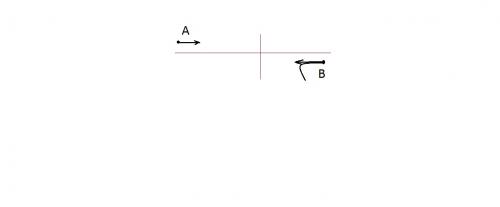
Это задача качественная. Может в чем-то и полезная. Сделаем рисунок.
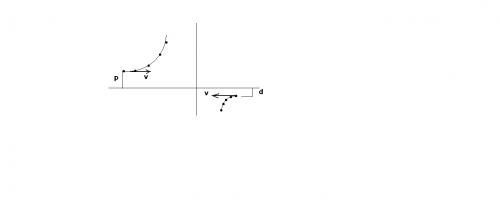
Воспользуемся законом сохранения момента импульса (который в базовой школе не изучается):
mvp = 2mvd, откуда p = 2d, т.е. отклонение левой частицы в 2 раза больше. При d → | – ∞ | p → + ∞.
Соскучились по задачам со звездочкой?
Задача 12. На гладком полу стоит сосуд, заполненный водой плотностью ρ0; Объем воды V0. Оказавшийся на дне сосуда жук объема V и плотностью ρ через некоторое время начинает ползти по дну сосуда со скоростью uотносительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды все время остается горизонтальным.
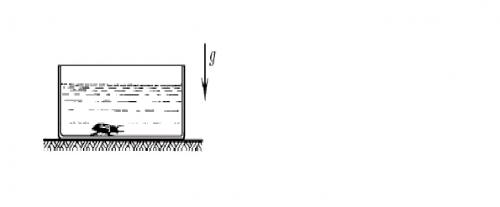
Это задача на движение центра масс. Внешними силами будут вертикальные силы P’ж = Рж – ρ0gV, где Рж = ρgV – сила тяжести жука, N – сила реакции опоры (см. рисунок). На направление оси Х проекции этих сил равны нулю. В начальный момент скорость центра масс равна нулю хс = 0.
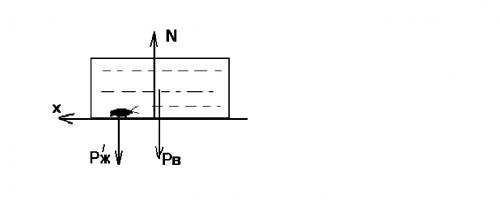
Пусть перемещение сосуда равно ξ2 = x, а перемещение жука равно ξ1 = – (L – x) . Тогда ξ1P’ж + ξ2 Р0 = 0 . Это уравнение (и ему подобное надо запомнить), Оно означает, что если система замкнута, то положение центра масс, даже если тела системы перемещаются, остается неизменным. Запищем последнее равенство в виде: Р0x – P’ж ·(L – х). Решим относительно х:
x = L(ρ – ρ0) /[ρV -ρ0(V0 – V)]. Разделим на время t, получим: v = u(ρ – ρ0)V / (ρV + ρ0V0). Здесь мы учли, что V << V0.
Задача очень полезна и поучительна. В частности, например, для задачи, когда человек переходит с носа лодки на корму.
Задача 13. На гладкой горизонтальной плоскости находится клин с углом α при основании. Тело массы m, положенное на клин, опускается с ускорением, направленным под углом β > α к горизонтали. Определите массу клина.
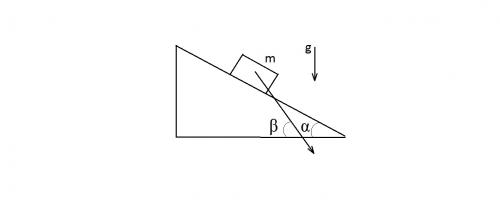
Эта задача без звездочки. Кажется, что ее надо решать стандартно. Однако есть подводные камни. Поступим следующим образом: разложим ускорение тела а0 в горизонтальном направлении a1 и вдоль наклонной плоскости a (см. рисунок):
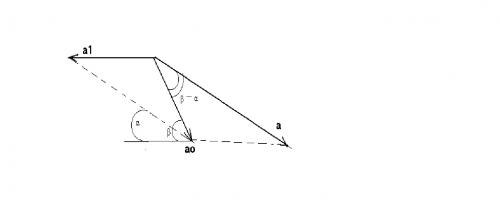
Воспользуемся теоремой синусов: a1 / sin(β – α) = a / sin(π – β).
Где a1 – ускорение клина, которое возникает под действием тела, а точнее – под действием силы инерции ma cos α. Т.е. Ma1 = ma cos α.
Подставляя значение ускорения, получим Ma·sin(β – α) / sin β = ma cos α.
Откуда, после несложных преобразований, получим M = m tg α / (tg β – tg α). Это ответ. Надеюсь, что задача полезная в плане обогащения опытом.
Напомню формулу sin(β – α) = sin β cos α – cos β sin α.
Задача 14. Груз массы m, подвешенный на пружине жесткости k, находится на подставке. Пружина при этом не деформирована. Подставку быстро убирают. Определите максимальное удлинение пружины и максимальную скорость груза.
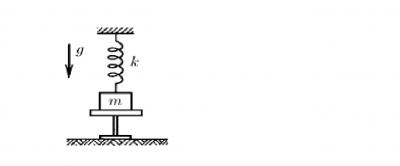
Рассмотрим систему тел – пружину и груз. Запишем изменение потенциальной энергии этой системы.
В начальном состоянии Ep1 = 0. В конечном состоянии Ep2 = kx2 / 2 -mgh.
Полное изменение потенциальной энергии равно нулю, отсюда следует, что
kx2макс / 2 = mgh, а максимальное удлинение xмкас = 2mg / k.
Груз под действием пружины начнет колебаться, уравнение колебаний будет иметь вид:
x = xмакс sin ωt, скорость колебаний vмакс = xмакс ω, где ω = (k / m)1/2. Подставляем это значение, получим
vмакс = 2mg / k ·(k / m)1/2 = 2g(m / k)1/2. Несложная задача.
Задача15. Тело массы m, подвешенное на пружине жесткости k, лежит на доске таким образом, что пружина не деформирована. Доску начинают опускать с ускорением а. Чему равно удлинение пружины в момент отрыва тела от доски? Каково максимальное удлинение пружины?
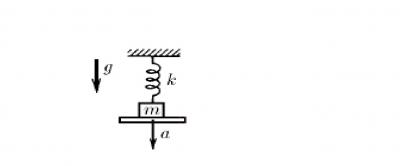
Опять задача со звездочкой. Она решается вполне стандартно. Но пришлось потратить на нее немалое время. Сделаем рисунок и расставим силы. На тело действуют силы упругости, сила реакции опоры, сила тяжести. Само тело движется ускоренно. Запишем второй закон Ньютона: ma = mg – N -kx.
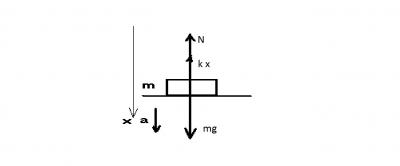
В момент отрыва N = 0, тогда удлинение в момент отрыва составит
x = m(g – a)/g (1)
Найдем скорость тела в момент отрыва: x = v2/2a, откуда с учетом (1), получим
v2 = 2am(g – a) / k. (2)
После отделения подставки тело, за счет инертности, продолжит движение до тех пор, пока не остановится. Пусть оно остановится в точке x0.
Поскольку диссипативных сил нет и внешние силы отсутствуют, то полная энергия после отделения подставки, остается постоянной. Найдем изменения энергии тел, входящих в систему. Изменение кинетической энергии тела равно:
ΔEk = 0 – mv2/2 = – mv2/2.
Изменение потенциальной энергии тела: ΔEp1 = – mg(x0 – x). Знак ” – ” означает убыль потенциальной энергии тела.
Изменение потенциальной энергии пружины составит: ΔEp2 = kx02 /2 – kx2 /2. Сумма этих изменений энергий равна нулю:
ΔEk + ΔEp1 + ΔEp2 = 0. Подставляя эти значения, после некоторых алгебраических преобразований, получим квадратное уравнение:
x20 – (2mg/k)·x0 – 2m2ag/k2 + m2a2/k2 + m2g2/k2 = 0
Решение которого и даст наибольшее отклонение: x0 = m(g + √2ag -a2) / k. Это второй ответ. Конечно, эта задача высокого уровня или олимпиадного. Но тренироваться надо на трудных задачах.
Задача 16. На горизонтальной плоскости лежат два бруска массы m1 и m2, соединенных недеформированной пружиной. Определите, какую наименьшую постоянную силу нужно приложить к левому бруску, чтобы сдвинулся и правый, если коэффициент трения грузов о плоскость µ.
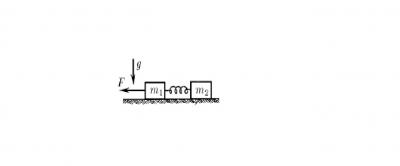Делать рисунок не будем. Будем считать, что скорость перемещения первого тела небольшая, тогда работа внешней силы F и работа силы трения, действующей на первое тело равно изменению потенциальной энергии пружины ΔEp = A – Aтр. Или kx2/2 = Fx – μm1gx, откуда kx = 2F -2μm1g. С другой стороны, условие трогания с места второго тела является kx ≥ μm2g. С учетом этого наибольшая сила равна
2F = 2μm1g + μm2g или F = μg(m1 + m2/2) . Подумайте, почему надо найти именно наименьшую силу.
Задача 17. На каком минимальном расстоянии от места закругления склона должна располагаться стартовая площадка лыжников, чтобы они, достигнув закругления, начали свободный полет? Угол склона α, радиус его закругления R, коэффициент трения между лыжами и снегом μ < tg α. Стартовой скоростью лыжников пренебречь.
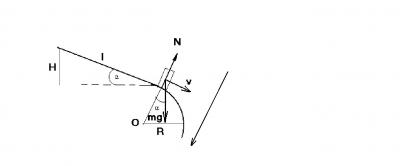Похожие задачи встречаются в ЕГЭ (Я видел задачу, когда тело въезжает на наклонную плоскость, а затем по закруглению). Эта задача на стыке динамики и закона сохранения энергии. Сделаем рисунок и расставим силы.
Запишем второй закон Ньютона на направление, указанное стрелкой: maц = mgcosα – N или mv2/R = mgcosα – N. Выразим силу реакции опоры N = mg cosα – mv2/R. Свободный полет будет тогда, когда сила реакции опоры обратится в нуль (N = 0).
Из этого условия найдем скорость v2 =gR cosα или v = √ gR cosα. Запишем для лыжника значение потенциальной и кинетической энергий в начальном и конечном положениях.
Ep1 = mgh, Ek1 = 0, Ep2 = 0, Ek2 = mv2/2. Изменения этих энергий равны ΔEp = – mgh, ΔEk = mv2/2. Т.к. ΔEp + ΔEk = – Aтр
т.е. mv2/2 – mgh = – μmgl cos α. Здесь Fтр = μmg cos α, Aтр = – Fтрl.
Это ответ. Теперь становится ясным, почему в задаче оговорено условие А в самом деле почему?
Источник