Сосуд с жидкостью в лифте
- Главная
- Вопросы & Ответы
- Вопрос 6901097
более месяца назад
Просмотров : 28
Ответов : 1
Лучший ответ:

comment
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Как называются парные, одинаковые хромосомы соматической клетки? Как называются парные, одинаковые хромосомы соматической клетки?
более месяца назад
Смотреть ответ
Просмотров : 38
Ответов : 1
Сколько хромосом и ДНК в различных периодах интерфазы? Сколько хромосом и ДНК в различных периодах интерфазы?
более месяца назад
Смотреть ответ
Просмотров : 12
Ответов : 1
Какой набор хромосом в соматических и половых клетках? Какой набор хромосом в соматических и половых клетках?
более месяца назад
Смотреть ответ
Просмотров : 35
Ответов : 1
Как называется набор хромосом, характерный для вида? Как называется набор хромосом, характерный для вида?
более месяца назад
Смотреть ответ
Просмотров : 18
Ответов : 1
Что образуется из интегументов (покровов семязачатка)? Что образуется из интегументов (покровов семязачатка)?
более месяца назад
Смотреть ответ
Просмотров : 15
Ответов : 1
Источник
Чивилев В.И. Закон Архимеда //Квант. — 1987. — № 1. — С. 29-30.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
«…Удар сжатого воздуха хлопнул в трубах, вода в цистерне зажурчала, и глубомер пополз вверх. Лодка всплыла на ровном киле, и глубомер показал, что рубка уже вышла из воды»,— так описывается всплытие подводной лодки в книге Л. Соболева «Морская душа».
Причина всплытия — сила Архимеда, называемая еще выталкивающей силой, которая после продувки цистерн с водой сжатым воздухом превысила по модулю силу тяжести лодки. Когда же и в каком случае возникает сила Архимеда? Со стороны чего она действует? Куда приложена, как направлена и чему равна?
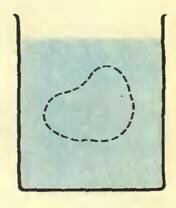
Выталкивающая сила — это сумма всех сил давления, действующих со стороны жидкости или газа на поверхность погруженного в нее тела (рис. 1). Истинная причина появления выталкивающей силы — наличие различного гидростатического давления на разных уровнях жидкости.
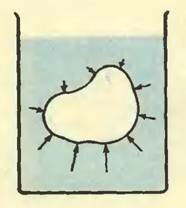
Рис. 1
Для нахождения силы Архимеда мысленно заменим погруженное тело жидкостью в объеме этого тела (рис. 2).

Рис. 2
На нее со стороны окружающей жидкости будет действовать такая же выталкивающая сила, как и на погруженное тело. По третьему закону Ньютона выделенная в объеме тела жидкость (вытесненная жидкость) будет действовать на окружающую жидкость с той же самой по модулю, но противоположно направленной силой. Это — вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета (необязательно инерциальной), называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.
Итак, выталкивающая сила, действующая на погруженное в жидкость тело, равна по модулю и противоположна по направлению весу вытесненной жидкости. Это и есть закон Архимеда. Заметим, что в формулировке закона говорится именно о весе вытесненной жидкости, а не о силе тяжести. И это весьма существенно, так как вес тела (по модулю) не всегда совпадает с силой тяжести. Например, ящик массой m в кабине поднимающегося с ускорением а лифта давит на пол с силой m(g + a). Это значит, что вес ящика равен Р = m(g + a), в то время как сила тяжести, действующая на ящик, равна mg. Когда же кабина лифта опускается с тем же ускорением, вес ящика оказывается равным Р = m(g – a).
Из последнего выражения ясно, что выталкивающая сила появляется тогда, когда нет состояния невесомости, то есть любое тело (в том числе и жидкость) имеет вес. Если сосуд с жидкостью свободно падает, то жидкость находится в состоянии невесомости и на погруженное в нее тело сила Архимеда не действует. Не действует эта сила и в космическом корабле, движущемся с выключенными двигателями.
При доказательстве закона Архимеда мы считали, что тело полностью погружено в жидкость и вся его поверхность соприкасается с жидкостью. Если же часть поверхности тела плотно прилегает к стенке или дну сосуда, так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Яркой иллюстрацией сказанного служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Брусок не всплывает, так как со стороны воды на него действует сила, не выталкивающая его вверх, а прижимающая ко дну (рис. 3).
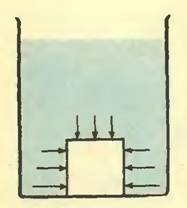
Рис. 3
Приведенная формулировка закона Архимеда остается справедливой и в случае, когда тело лишь частично опущено в жидкость, но не соприкасается со стенками сосуда. (Доказательство аналогично случаю полностью погруженного в жидкость тела.)
Нам осталось научиться находить вес вытесненной жидкости и линию действия выталкивающей силы. В общем случае (например, когда тело погружено в жидкость, вращающуюся вместе с сосудом) это не так легко сделать.
Рассмотрим наиболее простой и часто встречающийся на практике случай. Пусть сосуд с жидкостью неподвижен в некоторой инерциальной системе отсчета. Тогда, как известно, вес любого неподвижного тела равен силе тяжести, действующей на тело. Поэтому и выталкивающая сила равна по модулю силе тяжести, действующей на вытесненную жидкость, и противоположно ей направлена. Линия действия выталкивающей силы будет проходить через центр тяжести вытесненного объема жидкости. Покажем это.
На вытесненный объем жидкости массой m (рис. 4) действуют две силы — сила тяжести (~m vec g), приложенная в центре тяжести этого объема, и выталкивающая сила (~vec F_B). Так как жидкость находится в равновесии, то по правилу рычага (см. § 62 «Физики 6-7» или § 47 «Физики 8») действующие на нее силы обратно пропорциональны плечам этих сил. Плечо силы тяжести относительно оси, проходящей через центр тяжести, равно нулю. Значит, и плечо выталкивающей силы тоже равно нулю, т. е. линия действия выталкивающей силы проходит через центр тяжести «вытесненного» объема жидкости.
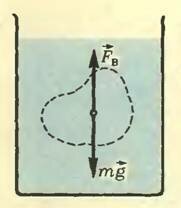
Рис. 4
Поскольку точку приложения силы можно переносить вдоль линии ее действия, обычно выталкивающую силу помещают в центр тяжести вытесненной жидкости и называют эту точку также центром давлений.
Источник
5. Механика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке представлены графики зависимости давления (p) от глубины погружения (h) для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре. 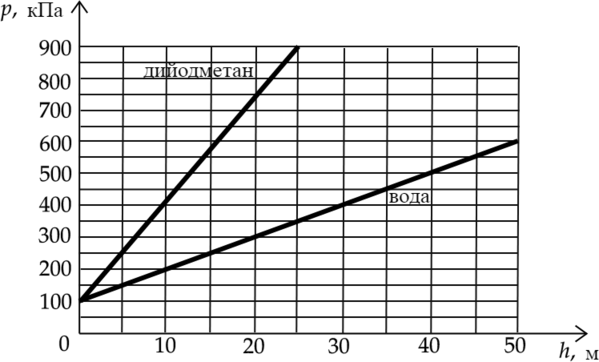
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
2) Плотность керосина 0,82 г/см(^3), аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
3) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
4) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
5) Плотность оливкового масла 0,92 г/см(^3), аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Полное давление (p) складывается из атмосферного давления (p_a) и гидростатического давления столба жидкости: [p=rho gh+p_a] 1) Как видно из графика, давление воды на глубине 10 м принимает значение 200 кПа, что в два раза больше атмосферного давления (Атмосферное давление 100 кПа).
Утверждение 1 – (color{red}{small text{Неверно}})
2) Так как плотность керосина меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 2 – (color{red}{small text{Неверно}})
3) Давление в воде на глубине 25 м равно 350 кПа, что в 3,5 раза больше атмосферного.
Утверждение 3 – (color{red}{small text{Неверно}})
4) Так как прямая давления в дийодметане лежит выше прямой давления в воде, то это означает, что давление в дийодметане возрастает быстрее, чем в воде.
Утверждение 4 – (color{green}{small text{Верно}})
5) Так как плотность оливкого масла меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 45
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см(^3), плотность жидкости 800 кг/м(^3), объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.
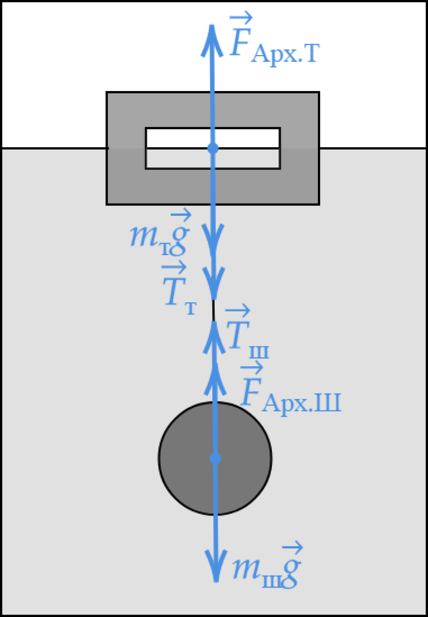
Запишем первый закон Ньютона для тела и шарика: [F_{text{Арх Т}}-m_{text{Т}}g-T=0] [F_{text{Арх Ш}}-m_{text{Ш}}g+T=0]
Сложим два уравнения: [F_{text{Арх Т}}-m_{text{Т}}g+F_{text{Арх Ш}}-m_{text{Ш}}g=0]
Обозначим плотность жидкости (rho_1), плотность материала (rho_2=2rho_1) [rho_1gV_1-rho_2cdot frac{1}{4}V_{T} g+rho_1 g cdot frac{1}{4} V_{T}-rho_2cdot frac{1}{4} V_{T} g=0] [rho_1V_1-2rho_1cdot frac{1}{4}V_{T} +rho_1 cdot frac{1}{4} V_{T}-2rho_1cdot frac{1}{4} V_{T} =0] [V_1-2cdot frac{1}{4}V_{T} + frac{1}{4} V_{T}-2cdot frac{1}{4} V_{T} =0] [V_1=frac{3}{4}V_T]
Тело плавает, погруженное на 3/4 своего объёма.
1) Сила Архимеда, действующая на тело, равна (displaystyle F_{text{Арх Т}}=rho_1gfrac{3}{4}V_T), а сила Архимеда, действующая на шар (displaystyle F_{text{Арх Т}}=rho_1gfrac{1}{4}V_T).
Утверждение 1 – (color{red}{small text{Неверно}})
2) [T=m_{text{Ш}}g-F_{text{Арх Ш}}]
Утверждение 2 – (color{red}{small text{Неверно}})
3) [T=F_{text{Арх Т}}-m_{text{Т}}g]
Утверждение 3 – (color{green}{small text{Верно}})
4) Модуль силы тяжести тела:[m_{text{Т}}g=rho_2cdot frac{1}{4}V_{T}g] Модуль силы тяжести шарика: [m_{text{Ш}}g=rho_2cdot frac{1}{4}V_{T}g]
Утверждение 4 – (color{green}{small text{Верно}})
5) Объём погружённой части тела равен (dfrac{3}{4}) объёма этого тела.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 34
Ученик помещал цилиндр, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погруженной в жидкость части цилиндра (V_text{ погр}). По результатам измерений он получил зависимость, представленную на графике объема погруженной части цилиндра (V_text{погр}) от плотности жидкости (rho). Объем цилиндра постоянен и равен (V=10) см(^3)
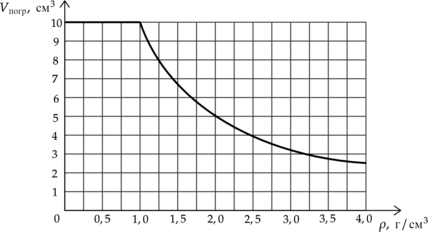 [begin{array}{|c|c|c|c|c|c|c|c|}
[begin{array}{|c|c|c|c|c|c|c|c|}
hline
text{Жидкость}&text{Бензин}&text{Спирт}&text{Вода}&text{Глицирин}&text{Хлороформ}&text{Бромоформ}&text{Дийодметан}\
hline
text{Плотность $rho$ г/см$^3$}&0,71&0,79&1,0&1,26&1,49&2,89&3,25\
hline
end{array}]
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) В бензине и воде сила Архимеда, действующая на цилиндр, одинакова.
2) Цилиндр не тонет в глицерине.
3) На цилиндр, погруженный в бромоформ, действует сила Архимеда 200мН.
4) Цилиндр плавает во всех жидкостях, указанных в таблице.
5) При плавании цилиндра в глицирине и бромоформе сила Архимеда, действующая на него, одинакова.
1) В бензине и в спирте цилиндр погружен на одинаковый объем. В таком случае сила Архимеда равна [F_A=rho gV_text{погр},] где (rho) – плотность жидкости, в которую погружено тело.
Но плотность спирта больше плотности бензина, а значит и сила Архимеда, действущая на цилиндр в спирте, больше силы Архимеда, действующей на цилиндр в бензине.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Цилиндр тонет при плотности меньше, чем 1 г/см(^3), у глицирина плотность 1,26 г/см(^3), значит, цилиндр плавает.
Утверждение 2 – (color{green}{small text{Верно}})
3) У бромоформа плотность больше 1 г/см(^3), а значит сила Архимеда уравновешивает силу тяжести.
По графику видим, что цилиндр начинает плавать при плотности жидкости 1г/см(^3), а значит именно такова плотность материала, из которого он сделан. Откуда сила Архимеда, действующая на цилиндр [F_A=mg=1text{ г/см$^3$}cdot 10text{ см$^3$}cdot 10text{ Н/кг}=100text{ мН}] Утверждение 3 – (color{red}{small text{Неверно}})
4) Нет, при плотности меньше 1 г/см3 цилиндр не плавает.
Утверждение 4 – (color{red}{small text{Неверно}})
5) У глицирина и бромоформа плотность больше 1 г/см(^3), а значит сила Архимеда уравновешивает силу тяжести и силы Архимеда одинаковы.
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 25
На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок). 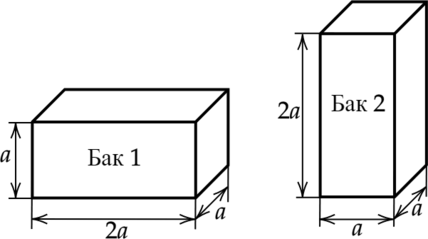
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление воды на дно первого бака в 4 раза меньше, чем на дно второго.
2) Первый бак давит на пол лифта с силой, в 2 раза меньшей, чем второй.
3) Сила давления воды на дно первого бака в 2 раза меньше, чем на дно второго.
4) Первый бак оказывает на пол лифта в 2 раза меньшее давление, чем второй.
5) Если лифт начнёт движение вниз с ускорением 2 м/с(^2), давление воды на дно баков уменьшится на 20 %.
1) Давление воды на дно первого бака равно [displaystyle p_1=frac{mg}{2a^2}] где (m) — масса воды. Давление на дно второго бака [displaystyle p_2=frac{mg}{a^2}] Видно, что давление (p_2=2p_1), следовательно, давление воды на дно первого бака в 2 раза меньше, чем на дно второго бака.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Сила давления равна силе тяжести воды. Так как объем одинаковый, значит масса воды в сосудах одинаковая.
Утверждение 2 – (color{red}{small text{Неверно}})
3) Утверждение 3 – (color{red}{small text{Неверно}})
4) Утверждение 4 – (color{green}{small text{Верно}})
5) При движении лифта вниз с ускорением 2 м/с(^2), оно будет компенсировать ускорение свободного падения (g), то есть вода будет иметь ускорение свободного падения 10-2=8 м/с(^2). В результате сила давления на дно баков будет равна (F=8m).
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 45
В сосуд с жидкостью погружают маленький датчик манометра, который регистрирует давление, создаваемое только столбом жидкости (без учёта атмосферного давления). На рисунке представлен график зависимости показаний (p) этого датчика давления от времени (t). Известно, что датчик может либо двигаться строго по вертикали вниз со скоростью 1 мм/с, либо покоиться. 
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) Максимальная глубина погружения датчика давления равна 20 см.
2) В промежутке времени от 50 с до 150 с датчик давления находился на одной и той же глубине.
3) Плотность жидкости, в которую опустили датчик давления, равна 650 кг/м(^3).
4) Максимальная глубина погружения датчика давления равна 15 см.
5) Плотность жидкости, в которую опустили датчик давления, равна 1300 кг/м(^3).
1) Датчик двигался на промежутках от 0 с до 50 с и от 150 с до 200 с, т. е. глубина погружения (h=1 cdot (50 + 50 ) = 100) мм(= 10) см.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Из графика видно, что давление не изменяется в промежутке времени от 50 с до 150 с, это означает что датчик находился на одной и той же глубине, т. е. покоился.
Утверждение 2 – (color{green}{small text{Верно}})
3) Давление столба жидкости: [p=rho gh] Плотность жидкости: [rho=frac{p}{gh}=frac{p}{gupsilon t}=frac{650}{10cdot0,001cdot50}=1300 text{ кг/м$^3$}]
Утверждение 3 – (color{red}{small text{Неверно}})
4) Глубина погружения 10 см
Утверждение 4 – (color{red}{small text{Неверно}})
5) Плотность жидкости (rho=1300) кг/м(^3)
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 25
Источник
