Сосуд содержащий газ движется со скоростью
2017-05-27
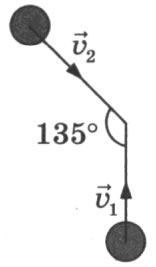
Сосуд, содержащий некоторую массу газа, движется со скоростью $u$. На сколько увеличится средний квадрат скорости теплового движения молекул при остановке сосуда для одноатомного и двухатомного газов? Теплоемкость, теплопроводность и масса стенок сосуда пренебрежимо малы.
Решение:
При движении сосуда все молекулы газа участвуют одновременно в хаотическом (тепловом) движении и направленном движении со скоростью $u$. При остановке сосуда молекулы по инерции некоторое время сохраняют свою направленную скорость, но затем в результате соударений друг с другом и со стенками сосуда газ придет в равновесное состояние, при котором молекулы его не обладают направленной скоростью. При этом установится максвелловское распределение молекул по скоростям с некоторым значением среднего квадрата скорости $langle v^{2} rangle_{2}$. Чтобы выяснить, насколько это значение больше того, что было до остановки сосуда ($ langle v^{2} rangle_{1}$), надо найти прирост средней кинетической энергии $Delta langle W_{0} rangle$ хаотического движения одной молекулы в результате остановки.
При движении сосуда результирующая скорость $vec{c}_{i}$, и кинетическая энергия поступательного движения любой молекулы соответственно равны:
$vec{c}_{i} = vec{v}_{i} + vec{u}, frac{m_{0} c_{i}^{2}}{2} = frac{m_{0}v_{i}^{2}}{2} + frac{m_{0}u^{2}}{2} + m_{0} vec{v}_{i} vec{u}$. (1)
Здесь $vec{v}_{i}$ — скорость хаотического движения молекулы.
Для нахождения средней кинетической энергии поступательного движения молекулы выражение (1) надо просуммировать по всем молекулам и затем разделить на общее число $N$ молекул:
$frac{1}{N} sum_{i=1}^{N} frac{m_{0} c_{i}^{2}}{2} = frac{1}{N} sum_{i=1}^{N} frac{m_{0}v_{i}^{2}}{2} + frac{m_{0}u^{2}}{2} + frac{m_{0} vec{u}}{N} sum_{i=1}^{n} vec{v}_{i}$. (2)
Вследствие хаотичности теплового движения, т. е. полной равноправности всех направлений вектора $vec{v}_{i}, sum vec{v}_{i} = 0$ и последнее слагаемое в правой части (2) обращается в нуль. Первое слагаемое можно представить как $m_{0} langle v^{2} rangle_{1} /2$. Тогда поступательная кинетическая энергия молекулы во время движения сосуда
$ langle W_{0п} rangle_{1} = frac{m_{0} langle v rangle_{1}}{2} + frac{m_{0}u^{2}}{2}$.
Очевидно, и средняя полная кинетическая энергия молекулы во время движения сосуда может быть выражена аналогичной суммой:
$langle W_{0} rangle^{ prime} = langle W_{0} rangle_{1} + m_{0} u^{2}/2$. (3)
Здесь первое слагаемое есть средняя полная энергия хаотического движения молекулы, равная $ikT_{1}/2$. После остановки сосуда
$langle W_{0} rangle^{ prime prime} = langle W_{0} rangle_{2} = (i/2)kT_{2}$. (4)
Если учесть сделанные в условии задачи оговорки, свидетельствующие о том, что сосуд не участвует в энергетическом балансе, то $langle W_{0} rangle^{ prime} = langle W_{0} rangle^{ prime prime}$, т. е. при остановке сосуда кинетическая энергия направленного движения каждой молекулы полностью переходит в энергию хаотического движения. Сравнивая (3) и (4), получим
$Delta langle W_{0} rangle = langle W_{0} rangle_{2} – langle W_{0} langle_{1} = m_{0} u^{2} /2$. (5)
Выражение (5) позволит найти искомое приращение среднего квадрата скорости теплового движения молекул.
Из выражения для средней энергии поступательного движения молекулы $m_{0} langle v^{2} rangle = frac{3}{2} kT$ следует, что
$langle v^{2} rangle = 3kT/m_{0}$.
Средняя полная кинетическая энергия одной молекулы
$langle W_{0} rangle = ikT/2$.
Совместное решение двух последних уравнений дает
$langle v^{2} rangle = 6 langle W_{0} rangle / (im_{0})$.
Тогда изменение среднего квадрата скорости
$Delta langle v^{2} rangle = langle v^{2} rangle_{2} – langle v^{2} langle_{1} = Delta langle W_{0} rangle frac{6}{im_{0}} $.
Учитывая выражение (5), находим
$Delta langle v^{2} rangle = 3u^{2}/i$.
Для одноатомного газа $(i = 3) Delta langle v^{2} rangle = u^{2}$. Для двухатомного газа $(i = 5) Delta langle v^{2} rangle = 0,6u^{2}$.
Источник
Тогда искомая часть молекул, которую необходимо определить
.
В нашем случае v=100 м/с; Δv=10 м/с; наиболее вероятная скорость v=(2RT/pm)1/2=376 м/с. Следовательно, u=v/vв=100/376, u2=0,071; Du=10/376; exp(–u2)=0,93.
Тогда
Ответ:ΔN/N=0,4%.
Задача 3
Сосуд, содержащий газ, движется со скоростью vo, затем быстро останавливается. На сколько увеличится при этом средний квадрат скорости теплового движения молекул газа в случаях: одноатомного газа, двухатомного газа? Газ считать идеальным.
Решение. Воспользуемся законом сохранения энергии. Пусть M масса газа в сосуде. Двигаясь со скоростью v газ, как целое, обладает кинетической энергией
.
Эта формула определяет кинетическую энергию направленного движения молекул, в котором они участвуют вместе с сосудом. После остановки сосуда направленное движение молекул в результате их соударений со стенками сосуда очень скоро превратится в хаотическое.
Пренебрегая теплообменом между газом и стенками сосуда за рассматриваемый промежуток времени, можно газ считать изолированной системой. Тогда из закона сохранения энергии следует, что «исчезнувшая» кинетическая энергия направленного движения молекул W должна быть равна приросту энергии хаотического движений молекул (приросту внутренней энергии DU):
Wк=DU.
Определим внутреннюю энергию газа. Для идеального одноатомного газа это есть энергия поступательного хаотического движения молекул:
,
где m – масса молекулы;
N – число молекул в сосуде.
Имеем
Отсюда следует, что изменение внутренней энергии одноатомного газа при торможении
DU=U2-U1= M[v2кв2-v2кв1],
где vкв1,vкв2 – средние квадратичные скорости молекул газа соответственно в начале и конце торможения.
Подставив в уравнение Wк=DU значения Wк и DU, получим первый ответ
v2кв2–v2кв1=v02.
Внутренняя энергия идеального двухатомного газа складывается из энергий поступательного и вращательного движения молекул. При этом три степени свободы приходятся на поступательное движение и две – на вращательное. В соответствии с законом о равномерном распределении энергии по степеням свободы, три пятых кинетической энергии W пойдет на увеличение энергии поступательного движения молекул и две пятых – на увеличение энергии их вращательного движения. Таким образом, имеем:
.
Из последнего соотношения получим второй ответ:
.
Ответ: 1) ; .
Задача 4
Какая часть молекул водорода, находящегося при температуре T, обладает скоростями, отличающимися от наиболее вероятной скорости не свыше чем на 5,0 м/с? Задачу решить для двух значений T: 1) 400 К, 2) 900 К .
Решение. Распределение молекул по скоростям выражается законом Максвелла: число молекул DN , относительные скорости которых лежат в интервале от u до u + Du:
где N – полное число молекул газа;
– функция распределения Максвелла;
u=v/vв – относительная скорость;
v – данная скорость;
vв – наиболее вероятная скорость.
Закон распределения Максвелла оказывается справедливым при условии Du<u. Поскольку в задаче идет речь о наиболее вероятной скорости, надо считать v=vв. Следовательно, u=v/vв=1 и выше написанное уравнение примет более простой вид:
.
Отсюда найдем ту часть молекул, относительные скорости которых лежат в интервале Du:
Прежде чем производить расчеты, необходимо убедиться в том, что выполняется условие Du<u. Так как u=v/vв , то Du=Dv/vв.
Чтобы вычислить Du , найдем сначала наиболее вероятную скорость при Т=400 К и Т=900 К по формуле:
:
vв1=2×8,31×400/0,002=1,82×103 м/с,
vв2=2×8,31×900/0,002=2,73×103м/с.
Подставляя эти значения vв и имея в виду, что Dv=10 м/с, поскольку в задаче идет речь о скоростях, лежащих в интервале от vв=–5,0 м/с до vв=5,0 м/с, получим:
Du1=1/182, Du2=1/273.
Так как u=1, видим, что условие Du<u выполняется для обеих температур.
Теперь найдем
DN1/N=4/((3,14)1/2×2,7×182)=0,0046,
DN2/N=4/((3,14)1/2×2,7×273)=0,0030.
Таким образом, при увеличении температуры наиболее вероятная скорость молекул увеличивается, а число молекул, скорости которых лежат в одном и том же интервале около наиболее вероятной, уменьшается.
Ответ: DN1/N=0,0046, DN2/N=0,0030.
Задача 5
Какая часть молекул газа имеет скорости превышающие наиболее вероятную?
Решение. В условии задачи речь идет о молекулах, скорости которых заключены в интервале от наиболее вероятной скорости v до v+Dv, т.е. в бесконечно большом интервале скоростей. Таким образом, условие применимости закона распределения скоростей, заключающееся в том, что Du<u, или Dv<v, здесь не выполняется. Поэтому от уравнения в форме:
надо перейти к дифференциальной форме этого закона
Полное число DN молекул, относительные скорости которых лежат в заданном интервале от u1 до u2, найдем, интегрируя правую часть в этих пределах:
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд — со вторым, второй — с третьим. Первоначально давление газа в сосудах было равно соответственно (р, 3р) и (р). В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
1) При первой открывании и закрывании кранов, в соответствии законам Дальтона и Бойля-Мариотта, установившееся давление во втором и третьем сосудах будет [dfrac{3p}{2}+dfrac{p}{2}=2p] 2) При втором открывании и закрывании, с учетом тех же законов, установившееся давление в первом и втором будет равно [dfrac{2p}{2}+dfrac{p}{2}=1,5p] 3) Так как объем сосуда не изменился, а температура по условию постоянна, то в соответствии закону Клайперона – Менделеева [pV=nu R T Rightarrow nu=dfrac{pV}{RT}] Знаменатель остался прежним, а числитель увеличился, значит и количество газа увеличилось.
Ответ:
Сжиженные газы с низкими температурами кипения хранят в открытых теплоизолированных резервуарах при нормальном давлении, с контактом с атмосферой. При таком хранении потери на испарение, отнесённые к единице массы сжиженного газа, уменьшаются при увеличении объёма сосуда. Объясните причины вышеизложенного, основываясь на известных физических законах и закономерностях.
1) Даже при хорошей теплоизоляции невозможно устранить полностью подвод тепла к сжиженным газам, значит, будет некоторое испарение вещества, потому что температура кипения таких газов ниже температуры атмосферы и существует теплопроводность.
2) Так как существует испарение, то в закрытых сосудах будет повышаться давление, что приведет к взрыву, поэтому газ хранят в открытых сосудах.
3) Подвод тепла к газу через стенки сосуда пропорционален площади стенок сосуда, а его масса пропорциональна объему. Объем же в свою очередь пропорционален кубу размеров сосуда. Поэтому с увеличением объема уменьшается испарение на единицу массы.
Ответ:
Чтобы вода в резервуаре быстрее закипела, источник тепла всегда помещают внизу. Желая охладить кастрюлю с горячей водой как можно быстрее, кастрюлю поставили на лёд. Является ли такой способ эффективным? Ответ поясните, указав какие физические явления и закономерности вы использовали для объяснения.
Нет, неверно.
Нагреватель ставится внизу, потому что нагретые слои воды, как более легкие, поднимаются вверх и таким образом достигается наиболее эффективное перемешивание и нагревание всей воды (по такому же принципу работает батарея в комнате). При охлаждении же дело происходит как раз наоборот: более холодные слои воды, как более тяжелые, опускаются вниз. Поэтому если поместить холодильник внизу, то перемешивания не будет, и остывание будет идти очень долго. Для более быстрого охлаждения надо поместить лед сверху.
Ответ:
На рисунке изображены графики двух процессов, проведённых с идеальным газом при одном и том же давлении. Графики процессов представлены на рисунке. Почему изобара (I) лежит выше изобары (II)? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.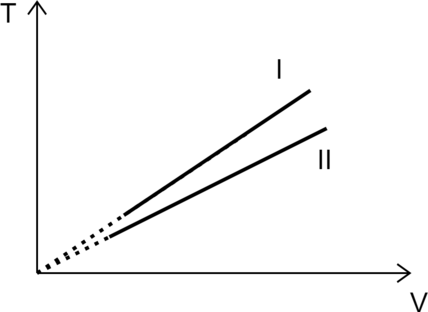 
1. Идеальный газ подчиняется закону Клапейрона–Менделеева: [pV=nu R T,] где (p) – давление газа, (V) – объем, (nu) – количество газа, (T) – температура газа в Кельвинах.
Выразим температуру [T=dfrac{pV}{nu R}] 2. Зафиксируем объем (V_0), при этом отношение температур равно [dfrac{T_I}{T_{II}}=dfrac{dfrac{pV_0}{nu_I R}}{dfrac{pV_0}{nu{II}R}}=dfrac{nu_{II}}{nu_{I}}>1] Значит количество газа во втором больше, чем количество газа в первом.
Ответ:
1 моль разреженного гелия участвует в циклическом процессе 1–2–3–4–1, график которого изображён на рисунке в координатах V–T, где V — объём газа, Т — абсолютная температура. Постройте график цикла в координатах p–V, где р — давление газа, V— объём газа. Опираясь на законы молекулярной физики и термодинамики, объясните построение графика. Определите, во сколько раз работа газа в процессе 2–3 больше модуля работы внешних сил в процессе 4–1.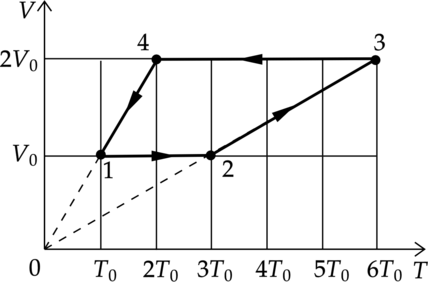 
Проанализируем процессы:
1–2: Процесс изохорный, по закону Шарля (dfrac{p}{T}=const), температура увеличилась в 3 раза, значит и давление увеличилось в 3 раза.
2–3: Процесс изобарный, по закону Гей–Люсака (dfrac{V}{T}=const) и объем и температура увеличились в 2 раза.
3–4: В процессе 3–4 газ изохорно уменьшил свою абсолютную температуру и давление в 3 раза.
4–1: Газ вернулся в первоначальное состояние Перестроим график цикла в координатах p–V (см. рисунок).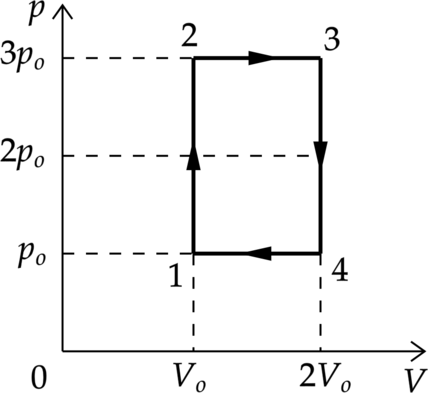 
Работа газа в процессе 2–3 равна [A_{23}=pDelta V=3p_(2V_0-V_0)=3p_0V_0] Работа внешних сил в процессе 4–1 равна [|A_{41}|=pDelta V=p_0(2V_0-V_0)=p_0V_0] Значит работа газа в процессе 2–3 в 3 раза больше работы внешних сил в процессе 4–1.
Ответ:
На рисунке 1 приведена зависимость внутренней энергии (U) 2 моль идеального одноатомного газа от его давления p в процессе 1–2–3. Постройте график этого процесса на рисунке 2 в переменных (p—V). Точка, соответствующая состоянию 1, уже отмечена на этом рисунке. Построение объясните, опираясь на законы молекулярной физики.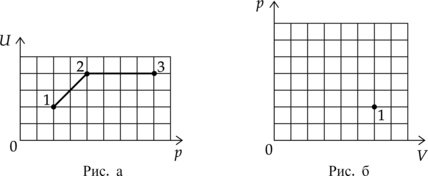 
1. Проанализируем процессы:
1–2: Внутренняя энергия прямо пропорциональна температуре газа (U=dfrac{3}{2}nu R T ), значит в процессе 1–2 температура увеличивается, давление тоже увеличивается (по графику ). По основному газовому закону (dfrac{pV}{T}=const) объем будет постоянен. График будет представлять собой вертикальную прямую
2–3: В процессе 2–3 внутренняя энергия газа постоянна, а значит и температура постоянна (по пункту 1), давление увеличивается, значит, по основному газовому закону объем будет уменьшаться. График будет представлять гиперболу.
2. Построим график
Ответ:
На графике представлена зависимость давления неизменной массы идеального газа от его плотности. Опишите, как изменяются в зависимости от плотности температура и объём газа в процессах 1–2 и 2–3.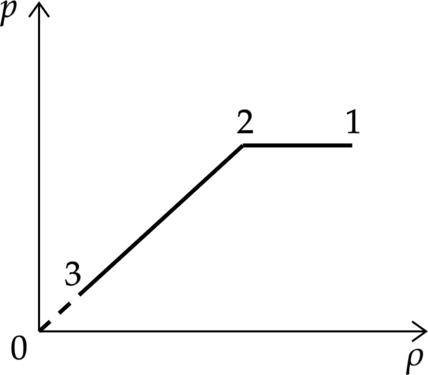 
1. Плотность находится по формуле: [rho=dfrac{m}{V} quad (1)] тогда уравнение Клайперона–Менделеева можно переписать в виде [pV=dfrac{m}{mu}RT Rightarrow p=dfrac{rho}{mu}RT, quad (2)] где (m) – масса газа, (V) – его объем, (T) – температура газа. 2. Процесс 1–2.
Плотность уменьшается при постоянном, в соответствии с формулой (1) объем будет увеличиваться, а температура будет увеличиваться в соответствии с формулой (2).
Процесс 2–3.
Плотность уменьшается вместе с давлением, причем давление уменьшается пропорционально плотности (p sim rho), а это означает, что температура газа постоянна, а по формуле (1) объем увеличивается.
Ответ:
Источник
При ознакомлении с демонстрационным вариантом контрольных измерительных материалов 2017 г. следует иметь в виду, что задания, включённые в демонстрационный вариант, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ в 2017 г. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2017 г., приведён в кодификаторе элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена 2017 г. по физике.
Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику ЕГЭ и широкой общественности составить представление о структуре будущих КИМ, количестве и форме заданий, об уровне их сложности. Приведённые критерии оценки выполнения заданий с развёрнутым ответом, включённые в этот вариант, дают представление о требованиях к полноте и правильности записи развёрнутого ответа.
Эти сведения позволят выпускникам выработать стратегию подготовки и сдачи ЕГЭ.
Инструкция по заполнению бланков ЕГЭ.
*) В конце теста вы найдете полное решение всех задач варианта.
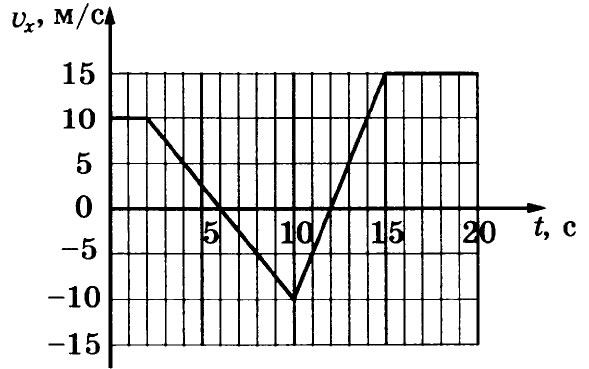
1. На рисунке приведён график зависимости проекции скорости тела их от времени. Чему
равна проекция ускорения этого тела ах в интервале времени от 10 до 15 с?
Ответ:
м/с2
2. У поверхности Земли на космонавта действует гравитационная сила 900 Н. Какая гравитационная сила действует со стороны Земли на того же космонавта в космическом корабле, который движется по круговой орбите на расстоянии двух радиусов Земли от земной поверхности?
Ответ:
Н
3. Одинаковые шары,массой 0,4 кг каждый движутся со скоростями, показан
ными на рисунке, и при столкновении слипаются. Чему будет равен суммарный импульс шаров после столкновения, если v1 = 4 м/с, v2 =v1√2?
Ответ:
кг·м/с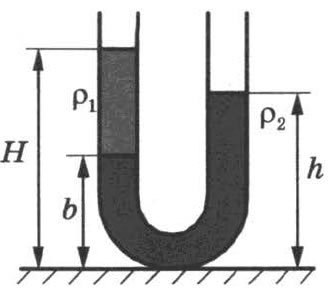
4. В широкую U-образную трубку, расположенную вертикально, налиты жидкости плотно
стью ρ1 и ρ2 (см. рисунок). Жидкости не смешиваются. На рисунке b = 15 см, h = 30 см,
Н = 35 см. Чему равно отношение плотностей ρ1/ρ2?
Ответ:
5. Четыре тела одинаковой массы 100 г двигались вдоль оси Ох. В таблице представлена
зависимость их координат от времени.
| t, с | 1 | 2 | 3 | 4 | 5 | |
| X1, см | 4 | 8 | 18 | 32 | 50 | |
| x2, см | 2 | 2 | 2 | 2 | 2 | 2 |
| X3, см | 2 | 4 | 6 | 8 | 10 | |
| x4, см | 2 | -2 | 2 |
Выберите из предложенных утверждений двау которые верно отражают результаты этого
опыта.
1) Первое тело двигалось равномерно.
2) Сумма сил, дейтсвующих на второе тело, равна нулю.
3) Скорость третьего тела равна 2 м/с.
4) Период колебаний четвертого тела равен 2 с.
5) В момент времени 3 с кинетическая энергия третьего тела была равна 0,4 Дж.
Ответы №№:
6. Шарик, брошенный от поверхности земли вертикально вверх с начальной скоростью v0,
поднялся на высоту Н, а затем упал обратно на землю. Что произойдет с ускорением шарика и его максимальной потенциальной энергией относительно земной поверхности, если
уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь.
Для каждой величины определите соответствующий характер ее изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Ускорение шарика. Максимальная потенциальная энергия относительно земной поверхности:
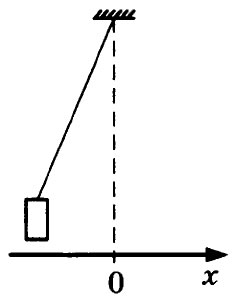7. Груз, привязанный к нити, отклонили от положения равновесия и отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин,
характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут
представлять.
К каждой позиции первого столбца подберите соответствующую позицию из второго
столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
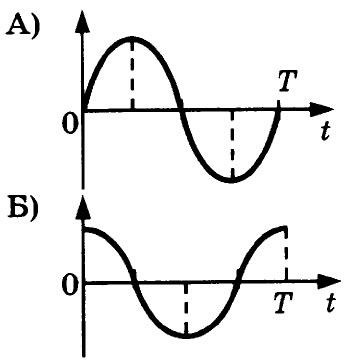 | 1) кинетическая энергия Ек 2) координата х 3) проекция импульса рх, 4) проекция ускорения ах |
Ответы АБ:
8. Объём 1 моль водорода в сосуде при температуре Т и давлении р равен 3 л. Чему равен
объём 3 моль водорода при том же давлении и температуре 2Т? (Водород считать идеальным газом.)
Ответ:
л
9. Кусок металла с удельной теплоёмкостью 450 Дж/(кг·К) нагрели от 20 °С до 60 °С,
затратив количество теплоты, равное 36 кДж. Чему равна масса этого куска металла?
Ответ:
кг
10. Газ в цилиндре расширился, совершив работу 150 Дж. Внутренняя энергия газа при этом
уменьшилась на 30 Дж. Какое количество теплоты газ получил от окружающих тел?
Ответ:
Дж
11. В жёстком закрытом сосуде находится влажный воздух при температуре 16 °С. Плотность водяных паров в сосуде равна 1,155·10-2 кг/м3. Воздух в сосуде нагревают до
25 °С. Пользуясь таблицей зависимости плотности насыщенных паров воды от температуры, выберите два верных утверждения о результатах этого опыта.
| t, °С | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| pнп, 10-2 кг/м3 | 1,36 | 1,45 | 1,54 | 1,63 | 1,73 | 1,83 | 1,94 | 2,06 | 2,18 | 2,30 |
1) При температуре 16 °С на стенках сосуда есть капельки росы.
2) Относительная влажность воздуха в сосуде при 18 °С равна 75%.
3) При увеличении температуры относительная влажность воздуха в сосуде уменьшается.
4) Давление в сосуде остаётся постоянным.
5) Плотность водяного пара в сосуде при нагревании увеличивается.
Ответы №№:
12. В ходе адиабатного процесса внутренняя энергия 1 моль разреженного гелия увеличивается. Как изменяются при этом температура гелия и его давление?
Для каждой величины определите соответствующий характер
изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
Температура гелия/ Давление гелия: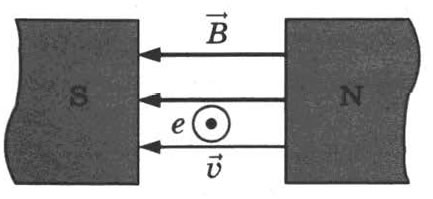 
13. Электрон е влетает в зазор между полюсами электромагнита со скоростью v→направленной к наблюдателю перпендикулярно плоскости рисунка (см. рисунок, где кружок с
точкой показывает направление движения электрона). Как направлена (вправо, влево,
вверх, вниз, к наблюдателю, от наблюдателя) действующая на него сила Лоренца F?→
Ответ запишите словом (словами).
Ответ:
14. Заряженная пылинка массой m с зарядом q движется с ускорением а = 20 м/с2 в однородном электрическом поле напряжённостью Е. Каково ускорение пылинки массой 2m
с зарядом 3q в том же поле? (Силой тяжести, действующей на пылинку, пренебречь.)
Ответ:
м/с2
15. Индуктивность одного витка проволоки равна 4·10-3 Гн. При какой силе тока магнитный поток через поперечное сечение катушки, сделанной из 5 витков, равен 20 мВб?
Ответ:
A
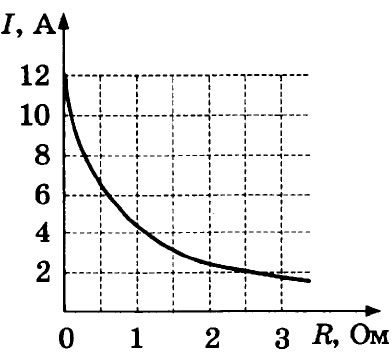
16. К аккумулятору подключили реостат. На рисунке показан график изменения силы тока
в реостате в зависимости от его сопротивления. Выберите из предложенных утверждений два у которые верно отражают результаты этого опыта.
1) Внутреннее сопротивление аккумулятора равно 0,5 Ом.
2) ЭДС аккумулятора равна 12 В.
3) Мощность, выделяемая в реостате увеличивается при увеличении его сопротивления.
4) Напряжение на реостате при силе тока 2 А равно 5 В.
Напряжение на источнике не зависит от силы тока через реостат.
Ответы №№: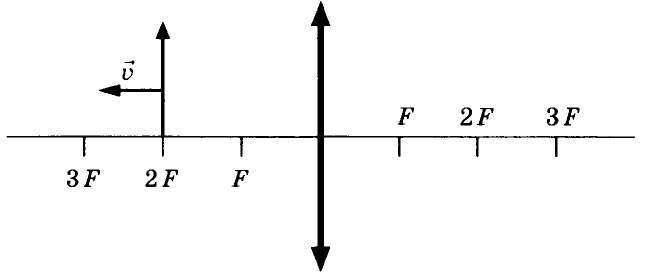 
17. Предмет, расположенный на двойном фокусном расстоянии от тонкой собирающей линзы, передвигают к тройному фокусу (см. рисунок). Как изменятся при этом расстояние
от линзы до изображения предмета и размер
изображения?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Расстояние от линзы до изображения. Размер изображения:
18. Участок цепи постоянного тока содержит резистор. Установите соответствие между формулами для вычисления физических величин и названиями этих величин.
В формулах использованы обозначения: I — сила тока на участке цепи; U — напряжение на участке цепи, t — время протекания тока.
К каждой позиции первого столбца подберите соответствующую позицию из второго
столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФОРМУЛЫ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| А) IU Б) It | 1) заряд, протекший через резистор 2) напряжение на резисторе 3) мощность тока, выделяющаяся на резисторе 4) сила тока через резистор |
Ответы АБ:
19. Ядро магния 2412Mg захватило электрон. Определите число протонов и нейтронов в этом
ядре, образовавшемся в результате такой реакции.
Число протонов. Число нейтронов:
20. На рисунке представлен фрагмент спектра излучения атомарных паров водорода. Цифры
на числовой оси — длины волн в нанометрах. Чему равна минимальная энергия фотонов
на данном участке спектра? Ответ округлить до целого значения.
Ответ:
·10-19Дж
21. В ядерном реакторе цепочка ядерных реакций начинается с захвата ядром быстрого
нейтрона. Как изменятся при захвате нейтрона следующие характеристики ядра: заряд
ядра и число нуклонов в ядре?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется.
Запишите выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
Заряд ядра. Число нуклонов в ядре:
22. С помощью амперметра проводились измерения силы тока на участке цепи. Шкала амперметра проградуирована в А. Погрешность измерений силы тока равна половине цены
деления шкалы амперметра. Запишите в ответ величину силы тока в цепи с учётом погрешности измерений.
Ответ: ( ±
) А
23.Необходимо собрать экспериментальную устаповку, с помощью которой можно определить ускорение тела, соскальзывающего с наклонной плоскости. Для этого школьник
взял брусок и наклонную плоскость. Какие два предмета из приведённого ниже перечня
оборудования необходимо дополнительно использовать для проведения этого эксперимента?
1) динамометр
2) пружина
3) секундомер
4) линейка
5) весы
Ответы №№:
24. Рассмотрите таблицу, содержащую некоторые характеристики планет Солнечной системы. Размеры и параметры орбит даны в сравнении с планетой Земля.
Выберите два утверждения, которые соответствуют характеристикам планет.
1) Средняя плотность Венеры меньше средней плотности Земли.
2) Центростремительное ускорение Юпитера при его вращении вокруг Солнца больше
центростремительного ускорения Марса.
3) Первая космическая скорость для Нептуна меньше, чем для Урана.
4) Ускорение свободного падения на Меркурии составляет примерно1 м/с2.
5) Сила притяжения Сатурна к Солнцу больше, чем у Юпитера.
| Имя | Диаметр | Масса | Орбитальный радиус (а.е.) | Период обращения (земных лет) | Период вращения (земных суток) | |
| Меркурий | 0,38 | 0,06 | 0,39 | 0,24 | 58,6 | |
| Венера | 0,95 | 0,82 | 0,72 | 0,62 | 243 | |
| Земля | 1 | 1 | 1 | 1 | 1 | |
| Марс | 0,53 | 0,11 | 1.5 | 1,9 | 1 | |
| Юпитер | 11,2 | 318 | 5.2 | 11,9 | 0,41 | |
| Сатурн | 9,5 | 95,2 | 9.5 | 29,5 | 0,43 | |
| Уран | 4 | 14,6 | 19.2 | 84 | 0,72 | |
| Нептун | 3,9 | 17,2 | 30,1 | 165 | 0,67 | |
Ответы №№: Часть II.
25. Снаряд, летящий со скоростью 100 м/с, разрывается на два осколка. Один из осколков
летит под углом 90° к первоначальному направлению, а второй — под углом 60°. Какова
масса снаряда до разрыва, если второй осколок массой 1 кг имеет скорость 400 м/с?
Массой взрывчатого вещества пренебречь.
Ответ:
кг
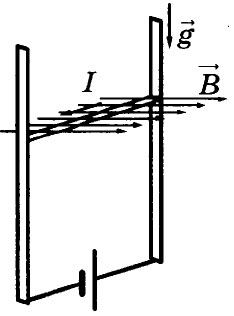
26. В однородном магнитном поле по вертикальным направляющим без
трения скользит прямой горизонтальный проводник массой 0,2 кг, по
которому течёт ток 2 А. Вектор магнитной индукции направлен горизонтально перпендикулярно проводнику (см. рисунок), В = 2 Тл. Чему
равна длина проводника, если известно, что ускорение проводника направлено вниз и равно 2 м/с2?
Ответ:
м
27. Предмет расположен на горизонтальной главной оптической оси тонкой собирающей
линзы. Оптическая сила линзы D = 5 дптр. Изображение предмета действительное, увеличение (отношение высоты изображения предмета к высоте самого предмета) k = 2.
Найдите расстояние от изображения предмета до линзы.
Ответ:
см
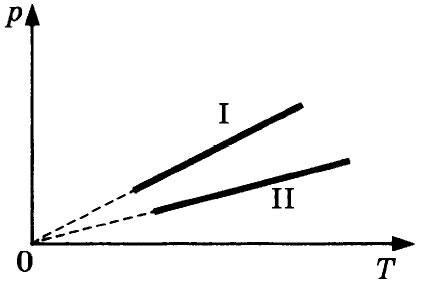
28. Две порции одного и того же идеального газа нагреваются
в сосудах одинакового объёма. Графики процессов представлены на рисунке. Почему изохора I лежит выше изохоры II? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.
1) ν1ν2
2) ν1 = ν2
3) ν1 > ν2
Ответ:
См. РЕШЕНИЕ.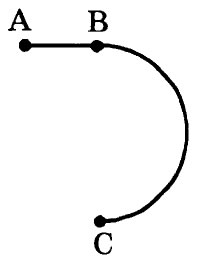
29. Стартуя из точки А (см. рисунок), спортсмен движется равноускоренно
до точки В, после которой модуль скорости спортсмена остаётся постоянным вплоть до точки С. Во сколько раз время, затраченное спортсменом на участок ВС, больше, чем на участок АВ, если модуль ускорения
на обоих участках одинаков? Траектория ВС — полуокружность.
Ответ:
См. РЕШЕНИЕ.
30. Два одинаковых теплоизолированных сосуда соединены короткой трубкой с краном.
Объём каждого сосуда V = 1 м3. В первом сосуде находится ν1 = 1 моль гелия при температуре Т1 = 400 К; во втором ν2 = 3 моль аргона при температуре Т2. Кран открывают.
После установления равновесного состояния давление в сосудах р = 5,4 кПа. Определите
первоначальную температуру аргона Т2.
Ответ:
К См. РЕШЕНИЕ.
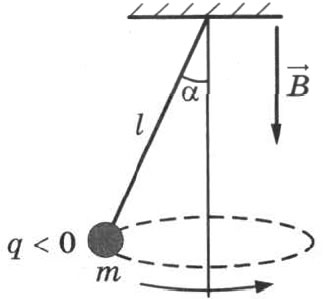
31. В однородном магнитном поле с индукцией В,→направленной вертикально вниз, равномерно вращается по окружности в горизонтальной плоскости против часовой стрелки отрицательно заряженный шарик массой m подвешенный на нити длиной l (конический
маятник). Угол отклонения нити от вертикали равен α, скорость вращения шарика равна
v. Найдите заряд шарика q. Сделайте рисунок с указанием сил, действующих на шарик. Вычислите результат, если B = 1 Тл, l= 71 см, α = 30°, v = 0,5 м/с, m = 1 г.
Ответ:
мКл См. РЕШЕНИЕ.
32. Фотокатод с работой выхода 4,42·10-19 Дж освещается монохроматическим светом. Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией
4·10-4 Тл перпендикулярно линиям индукции этого поля и движутся по окружностям.
Максимальный радиус такой окружности 10 мм. Какова частота ν падающего света?
Ответ:
·1015 Гц См. РЕШЕНИЕ.
Источник