Сосуд содержащий некоторое количество гелия
Всероссийская олимпиада школьников по физике (2016 – 2017 уч.г.)
Школьный этап, 11 класс
Решения
Задача 1.
Тело брошено под углом ɑ к горизонту со скоростью Jо, причём максимальная дальность полёта равна максимальной высоте подъёма. Найти угол ɑ, если сопротивлением воздуха можно пренебречь.
(10 баллов)
Возможное решение | |
Запишем уравнение движения тела на ось ОХ и ОУ: Sмакс= х = (1); (2), где t – время полета тела вдоль оси ОХ. Решая совместно уравнения (1) и(2) получим , Þ . Нmax можно найти по формуле . По условию задачи Sмакс Þ; ; Þ Þ ; . | |
Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин (; представлено полное верное объяснение с указанием наблюдаемых явлений и законов: ОХ: Sмакс= х = ОУ: Проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу: . | 1 1 1 1 2 1 2 1 |
Задача 2.
Вертикальный цилиндрический сосуд содержит под тяжелым поршнем массой М некоторое количество гелия. Какое количество тепла Q необходимо сообщить газу, чтобы его объем увеличился вдвое? Как изменится результат, если под поршнем будет находиться водород? Потерями тепла и внешним давлением пренебречь.

(10 баллов)
Возможное решение | |
Процесс расширения газа происходит при постоянном давлении, поэтому Q = ucрDТ, где u – количество молей газа, cр – теплоемкость газа при постоянном давлении. cр = cv + R, где cv – теплоемкость газа при постоянном объеме. Для гелия (одноатомный газ) cv =, cр =; для водорода (двух атомный газ) cv =, cр =. Газ находится при постоянном давлении р = (S – площадь сечения сосуда) и подчиняется уравнению состояния рV = uRT. Таким образом , Q = ucрDТ = . Для гелия Q1 = , для водорода Q2 = | |
Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин; представлено полное верное объяснение с указанием наблюдаемых явлений и законов: Q = ucрDТ для гелия cv =, cр = для водорода (двух атомный газ) cv =, cр = р = уравнение состояния рV = uRT Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: Q = Для гелия Q1 = для водорода Q2 = | 1 1 1 1 1 1 2 1 1 |
Задача 3.
Имеется источник тока с внутренним сопротивлением r = 20 Ом. Какое внешнее сопротивление нужно подключить к источнику, чтобы мощность, выделяющаяся на внешнем сопротивлении, отличалась от максимально возможной мощности на 25 %?
(10 баллов)
Возможное решение | |
Тепловая мощность, выделяющаяся на резисторе, имеющем сопротивление R, определяется законом Джоуля – Ленца P=UI , где I – сила тока в цепи, а U – напряжение на резисторе. Сила тока определяется законом Ома для полной цепи , а напряжение на резисторе – законом Ома для участка цепи U = IR Þ Мощность, выделяющаяся на внешнем сопротивлении P = I2R = Она будет максимальной при условии R = r Þ По условию задачи мощность, выделяющаяся на внешнем сопротивлении, отличалась от максимально возможной мощности на 25 % Þ P = 0,75 Pmax Þ Подставляя в полученную формулу числовые данные, находим Получили квадратное уравнение корнями которого являются: R1= 6,7 Ом; R 2= 60 Ом. | |
Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин; представлено полное верное объяснение с указанием наблюдаемых явлений и законов (законы Ома для участка цепи и полной цепи, закон Джоуля-Ленца): U = IR P = Мощность максимальна при условии R = r Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: P = 0,75 Pmax Представлен правильный ответ с указанием единиц измерения искомой величины R1= 6,7 Ом; R 2=60 Ом. | 1 1 1 1 1 1 1 1 2 |
| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 |
Источник
Б.М.Львовский,
школа № 1126, г. Москва
ПредисловиеПредставленный учебный Учитель физики и | |
Содержание
| |
Список
| |
Урок | |
| Решите задачу 2, a. Каково давление азота, если средняя квадратичная скорость его молекул 500 м/с, а его плотность 1,36 кг/м3? | |
Урок | |
Задачи | |
| Задача 1. Как изменится давление водорода, находящегося в закрытом сосуде, если каждая молекула распадется на отдельные атомы, а средние квадраты скоростей не изменятся? | |
| Задача 2. Имеются два одинаковых сосуда. В одном из них находится кислород, а в другом – азот. Число молекул каждого газа и средние квадраты их скоростей одинаковы. Давление кислорода равно 32 кПа. Чему равно давление азота? | |
| Задача 3. В результате нагревания газа в закрытом сосуде средняя квадратичная скорость молекул увеличилась в 2 раза. Как изменилось давление? | |
| Задача 4. В сосуд, содержащий некоторое количество атомов гелия, добавляют такое же число молекул водорода, имеющих среднюю кинетическую энергию теплового движения, равную средней кинетической энергии теплового движения атомов гелия. Во сколько раз изменится давление в сосуде? | |
| Задача 5. Рассчитайте силу удара молекулы газа о стенку сосуда, если она движется перпендикулярно стенке со скоростью u, масса молекулы m0, а время ее соударения со стенкой dt. | |
| Задача 6. Сколько ударов Z молекул о стенку площадью S = 1 м2 происходит за 1 с? | |
| Задача 7 (проблемная). Спутник объемом V = 1000 м3 заполнен гелием. Метеорит пробил в стенке спутника отверстие площадью S = 1 см2. Оцените время, за которое давление упадет на 1%. Температуру внутри спутника считать неизменной. Средняя квадратичная скорость атомов гелия v = 500 м/с. | |
Пример дистанционного
компьтерного урока, отмеченного в числе
лауреатов 2-го всероссийского конкурса
«Дистанционный учитель года-2000», который был
проведен Российской академией образования,
Институтом общего среднего образования РАО и
центром дистанционного образования «Эйдос».
Адрес оргкомитета: https://www.eidos.ru/dist_teacher/index.htm E-mail: eidos@mailru.com. Как мы теперь
видим, можно получать образование, не выходя из
дома. Было бы желание! – Ред.
Источник
11. МКТ и Термодинамика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке показана зависимость давления газа (p) от его плотности (rho) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.
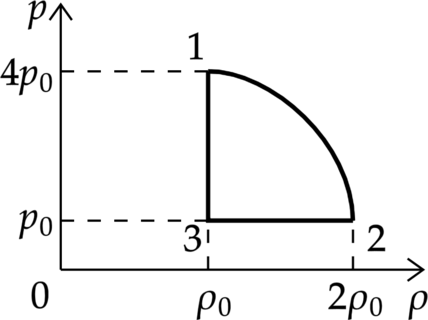
На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
“Демоверсия 2017”
1) По уравнению Клапейрона – Менделеева: [p=dfrac{rho}{mu}RT,] где (T) – температура, (mu) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – (color{green}{small text{Верно}})
2) Аналогично предыдущему пункту [p=dfrac{rho}{mu}RT] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – (color{red}{small text{Неверно}})
3) В процессе 2 – 3 плотность меньшается, а по формуле: [rho =dfrac{m}{V}] Объем увеличивается
Утверждение 3 – (color{red}{small text{Неверно}})
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – (color{green}{small text{Верно}})
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 14
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
“Демоверсия 2020”
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: [p=dfrac{nu R T}{V}] Парциальные давления гелия в левой и правой части одинаковы, одинаковы температуры и объёмы частей, следовательно, одинаковы и количества вещества гелия в левой и правой частях сосуда, то есть в левой и правой части сосуда будет содержаться по 2 моля гелия.
Найдём связь концентрации и количества вещества: [n=dfrac{N}{V}=dfrac{nu N_A}{V}] То есть концентрации и количества вещества зависят прямо пропорционально друг от друга, также заметим, что чем больше количество вещества, тем больше и количество молекул.
Найдём количество вещества аргона: [nu_{Ar}=dfrac{m_{Ar}}{mu_{Ar}}=dfrac{40text{ г}}{40text{ г/моль}}=1text{ моль}]
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) (color{red}{small text{Неверно}})
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) (color{green}{small text{Верно}})
Отношение давлений: [dfrac{p_text{ п}}{p_text{ л}}=dfrac{nu_text{ г.п}+nu_{Ar}}{nu_text{ г.л}}=dfrac{2text{ моль}+1text{ моль}}{2text{ моль}}=1,5] Где (nu_{text{ г.п.}},nu_{text{ г.л.}}) – количество вещества гелия в правой части, количество вещества гелия в левой части соответственно.
3) (color{red}{small text{Неверно}})
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) (color{red}{small text{Неверно}})
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: [U=dfrac{3}{2}nu R T] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) (color{green}{small text{Верно}})
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: [dfrac{p_{k}}{p_text{ н}}=dfrac{nu_{text{ г.п.}}+nu_{Ar}}{nu_{Ar}}=dfrac{2text{ моль}+1text{ моль}}{1text{ моль}}=3]
Ответ: 25
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: [pV=nu RT] где (nu) — количество вещества, (T) — температура в Кельвинах, (p) — давление газа, (V) — объем, занимаемый газом, (R) — универсальная газовая постоянная. Выразим объем [V=dfrac{nu RT}{p}] При нагревании газа объем увеличивается.
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Утверждение 2 — (color{green}{smalltext{Верно }})
3) Плотность газа: [rho=dfrac{m}{V}] При нагревании объем увеличивается, значит плотность уменьшается.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Сила Архимеда: [F_{text{Арх}}=rho gV] где (rho) — плотность газа, (V) — объем шарика, (g) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Концентрация: [n=dfrac{N}{V}] При нагревании газа объем увеличивается, концентрация уменьшается.
Утверждение 5 — (color{red}{smalltext{Неверно }})
Ответ: 24
На (pV)—диаграмме отображена последовательность трёх процессов (1 — 2 — 3) изменения состояния 2 моль идеального газа. 
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1 газ отдаёт положительное количество теплоты.
2) Процесс 2 является изотермическим.
3) В процессе 3 газ совершает работу.
4) В процессе 2 происходит расширение газа при постоянной температуре.
5) В процессе 1 происходит сжатие газа при постоянной температуре.
Работа газа находится как площадь под графиком 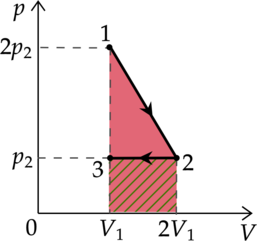
1) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. (Delta U=0), так как температура в процессе 1 не изменяется. При увеличении давления в изотермическом процессе объём уменьшается. (Delta V<0), следоватлеьно, (A<0). Таким образом, (Q<0), то есть газ отдает кол-во теплоты в данном процессе.
Утверждение 1 — (color{green}{smalltext{Верно }})
2) В процессе 2 температура увеличивается.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) (p=const), следовательно (Vsim T)
Температура уменьшается, то есть объем тоже уменьшается, (Delta V<0), (A<0)
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В процессе 2 температура увеличивается.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Температура в процессе 1 не изменяется. По закону Бойля-Мариотта (p V=const) так как давление увеличивается объём уменьшается.
Утверждение 5 —(color{green}{smalltext{Верно }})
Ответ: 15
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах (V-T), где (V) — объём газа, (T) — абсолютная температура газа. Количество вещества газа постоянно. 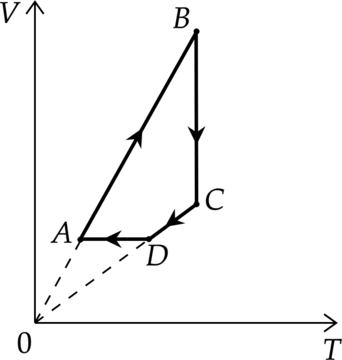
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) В состоянии (B) концентрация газа максимальна.
2) В процессе (AB) газ отдаёт некоторое количество теплоты.
3) В процессе (BC) внутренняя энергия газа увеличивается.
4) Давление газа в процессе (CD) постоянно, при этом внешние силы совершают над газом положительную работу.
5) В процессе (DA) давление газа изохорно уменьшается.
1) В точке (B) объем максимален, а концентрация минимальна:
Утверждение 1 —(color{red}{smalltext{Неверно }})
2) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. В процессе (AB) работа равна (0), температура увеличивается, то есть (Delta U>0), значит (Q>0), то есть газ получает тепло
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс (BC) — изотермический. Внутренняя энергия не меняется.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Процесс (СD) — изобарное сжатие. При уменьшении объема внешние силы совершают положительную работу.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Процесс (DA) — изохорное охлаждение ((psim T)). Следовательно, при уменьшении температуры давление уменьшается.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось. 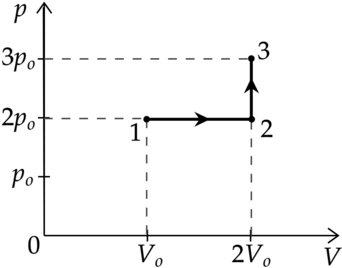
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1)Абсолютная температура газа минимальна в состоянии 2.
2)В процессе 1-2 абсолютная температура газа уменьшилась в 2 раза.
3)В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
4)Плотность газа максимальна в состоянии 1.
5)В ходе процесса 1-2-3 средняя квадратичная скорость теплового движения молекул газа увеличилась в (sqrt{3}) раза.
1) Уравнение состояния газа: [pV=nu RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещеста, (R) — универасальная газовая постоянная, (T) — температура. Температура максимальна там, где максимально произведение (pV), поэтому из графика видно, что (T_1 – min), (T_3 – max), (T_1<T_2<T_3)
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Процесс 1-2 — изобарное расширение ((Vsim T)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс 2-3 — изохорное нагревание. (V=const), следовательно (psim T) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В точке 1 — объем минимален, следовательно, плотность там максимальна.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) [E_{k}=dfrac{3}{2}kT] [dfrac{m_0 v^2}{2}=dfrac{3}{2}kT] где (m_0) — масса газа, (v^2) средняя квадратичная скорость [v^2sim T] [vsim sqrt{T}] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в (sqrt{3}) раз
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В левой части сосуда содержится 40 г неона, в правой — 2 моль гелия. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул неона. Температура газов одинакова и остаётся постоянной.
Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Внутренняя энергия гелия в сосуде меньше, чем внутренняя энергия неона.
2) Концентрация гелия в левой части сосуда в 2 раза больше концентрации неона.
3) В левой части сосуда общее число молекул газов в 3 раза больше, чем в правой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии меньше, чем в начальном.
5) В конечном состоянии давление в левой части сосуда в 3 раза больше, чем в правой.
1) Молярная масса неона (M=20) г/моль. Количество неона: [nu=dfrac{m}{M}=dfrac{40text{ г}}{20text{ г/моль}}=2 text{ моль}] Гелий займет все пространство сосуда, значит в левой части будет 3 моля вещества (1 моль гелия и 2 моль неона).
В правой части будет тоже 1 моль гелия.
Внутренняя энергия газа: [U=dfrac{i}{2}nu RT] Газы находятся при одинаковой температуре, количество гелия равно количеству неона. Внутренняя энергия гелия равна внутренней энергии неона
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) В левой части сосуда количество гелия в два раза меньше количества неона. Следовательно, концентрация гелия в два раза меньше концентрации неона.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Так как количество вещества в левой части сосуда больше в 3 раза, чем в правой, то и количество молекул также больше в 3 раза.
Утверждение 3 — (color{green}{smalltext{Верно }})
4) Так как температура гелия и общее количество гелия в сосуде не изменилось, то и внутреннняяя энергия не поменялась.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Давление газа: [p=nkT] Так как кол-во вещества в левой части сосуда больше в 3 раза, чем в правой, температуры одинаковые, то давление в конечном состоянии больше в левой части в 3 раза, чем в правой.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 35
Источник

