Сосуд содержит смесь газов
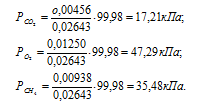
Команда “Газы!” была объявлена еще две недели назад. И что?! Легкие задачи порешали и расслабились?! Или вы думаете, что задачи на газы касаются только 28-х заданий ЕГЭ?! Как бы не так! Если газов пока еще не было в 34-х заданиях, это ничего не значит! Задач на электролиз тоже не было в ЕГЭ до 2018 года. А потом как врезали, мама не горюй! Обязательно прочитайте мою статью “Тайны задач по химии? Тяжело в учении – легко в бою!”. В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я – зритель в первом ряду.
Однако, вернемся к нашим баранам, вернее, Газам. Я прошла через огонь и воду вступительных экзаменов и знаю точно – хочешь завалить абитуриента, дай ему задачу на Газы. Почитайте на досуге сборник задач И.Ю. Белавина. Я процитирую одну такую “мозгобойню”, чтобы вам жизнь медом не казалась. Попробуйте решить.
И.Ю. Белавин, 2005, задача 229
“Два из трех газов (сероводород, водород и кислород) смешали и получили газовую смесь, плотность которой оказалась равной плотности оставшегося газа. Полученную газовую смесь вместе с равным ей объемом третьего газа под давлением поместили в замкнутый сосуд емкостью 4 л, содержавший азот при н.у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)”
Ну как, решили? Нет?! А ваши репетиторы?! Извините, это был риторический вопрос. Кстати, мои ученики, абитуриенты 2003-2008 гг. такие задачи щелкали, как семечки, на экзаменах во 2-й медицинский (теперь РНИМУ им. Н.И. Пирогова). Надеюсь, вам понятно, что 34-м задачам ЕГЭ еще есть куда усложняться, perfectio interminatus est (нет предела совершенству), с газами нужно работать, работать и работать. Поэтому команду “Газы!” отменять рано. Итак, поехали!
Сегодня мы поговорим о газовых смесях, затронем понятие плотности газа (абсолютной и относительной), средней молярной массы, решим задачи: определение средней молярной массы и плотности газа по компонентам смеси и наоборот.
• Газовая смесь – смесь отдельных газов НЕ вступающих между собой в химические реакции. К смесям газов относятся: воздух (состоит из азота, кислорода, углекислого газа, водяного пара и др.), природный газ (смесь предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и др.), дымовые газы (содержат азот, углекислый газ, пары воды, сернистый газ и др.) и др.
• Объемная доля – отношение объема данного газа к общему объему смеси, показывает, какую часть общего объема смеси занимает данный газ, измеряется в долях единицы или в процентах.
• Мольная доля – отношение количества вещества данного газа к общему количеству вещества смеси газов, измеряется в долях единицы или в процентах.
Секретная шпаргалка по химии. 4.2. Состав смеси газов
• Плотность газа (абсолютная) – определяется как отношение массы газа к его объему, единица измерения (г/л). Физический смысл абсолютной плотности газа – масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.
Секретная шпаргалка по химии. 4.2. Состав смеси газов
• Относительная плотность газа (плотность одного газа по другому) – это отношение молярной массы данного газа к молярной массе того газа, по которому она находится
Секретная шпаргалка по химии. 4.2. Состав смеси газов
• Средняя молярная масса газа – рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Настоятельно рекомендую запомнить среднюю молярную массу воздуха Мср(в) = 29 г/моль, в заданиях ЕГЭ часто встречается.
Обязательно посетите страницу моего сайта “Изучаем Х-ОбХ-04. Закон Авогадро. Следствия из закона Авогадро. Нормальные условия. Молярный объем газа. Абсолютная и относительная плотность газа. Закон объемных отношений”и сделайте конспекты по теории. Затем возьмите бумагу и ручку и решайте задачи вместе со мной.
ВАНГУЮ: чует мое сердце, что ЕГЭ по химии 2019 года устроит нам газовую атаку, а противогазы не выдаст!
Задача 1
Определить плотность по азоту газовой смеси, состоящей из 30% кислорода, 20% азота и 50% углекислого газа.
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 2
Вычислите плотность по водороду газовой смеси, содержащей 0,4 моль СО2, 0,2 моль азота и 1,4 моль кислорода.
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 3
5 л смеси азота и водорода имеют относительную плотность по водороду 12. Определить объем каждого газа в смеси.
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Несколько задач со страницы моего сайта
Задача 4
Плотность по водороду пропан-бутановой смеси равна 23,5. Определите объемные доли пропана и бутана
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 5
Газообразный алкан объемом 8 л (н.у.) имеет массу 14,28 г. Чему равна его плотность по воздуху
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 6
Плотность паров альдегида по метану равна 2,75. Определите альдегид
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Ну как? Пошло дело? Если туго, вернитесь к задачам и решайте их самостоятельно до тех пор, пока не щелкнет! А для стимуляции – десерт в виде еще одной задачи И.Ю. Белавина на газы. Наслаждайтесь ее решением самостоятельно!
И.Ю. Белавин, 2005, задача 202
“Сосуд емкостью 5,6 л при н.у. заполнили метаном, затем нагрели до высокой температуры, в результате чего произошло частичное разложение метана. Определите массу образовавшейся сажи, если известно, что после приведения к нормальным условиям объем полученной газовой смеси оказался в 1,6 раза больше объема исходного метана, эта газовая смесь обесцвечивает бромную воду и имеет плотность по воздуху 0,2931. (Ответ: m(C) = 0,6 г)”
Задачи И.Ю. Белавина – это крутой драйв! Попробуйте порешать, и вы откажетесь от просмотра любых ужастиков, поскольку запасетесь адреналином надолго! Но нам нужно спуститься на землю к ЕГЭ, простому и надежному, как первый советский трактор. Кстати, у меня в коллекции припасено немало сюрпризов с газовыми фишками, собранными за все годы работы и бережно хранимыми. Думаю, пришло время сказать им: “И снова здравствуйте!”, поскольку ЕГЭ с каждым годом становится “все чудесатее и чудесатее”. Но это уже совсем другая история. Читайте мои статьи – и вы подстелите соломку под свою ЕГЭшную попу.
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии https://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Позвоните мне +7(903)186-74-55, приходите ко мне на курс, на бесплатные Мастер-классы “Решение задач по химии”. Я с удовольствием вам помогу.
Репетитор по химии и биологии кбн В.Богунова
Источник
Задача 41.
Смешивают 0,04м3 азота, находящегося под давлением 96кПа (720мм. рт. ст.), с 0,02м3 кислорода. Общий объем смеси 0,06м3, а общее давление 97,6кПа (732мм. рт. ст.). Каким было давление взятого кислорода?
Решение:
По условию задачи объём азота увеличился в 1,5 раза (0,06/0,04 = 1,5), а объём кислорода – в 3 раза (0,06/0,02 = 3). Во столько же раз уменьшились парциальные давления газов.
Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). Отсюда Исходя из того, что объём кислорода до смешения был в три раза больше, чем после смешения, рассчитаем давление кислорода до смешения:
Ответ: Робщ. = 100,8кПа.
Задача 42.
Газовая смесь приготовлена из 2л Н2 (Р = 93,3 кПа) и 5л CH4 (Р = 112 кПа). Объем смеси равен 7л. Найти парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём водорода увеличился в 3,5 раза (7/2 = 3,5), а объём метана – в 1,4 раза (7/5 = 1,4). Во столько же раз уменьшились парциальные давления газов.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ:
Задача 43.
Газовая смесь состоит из NO и СО2. Вычислить объемное содержание газов в смеси (в %), если их парциальные давления равны соответственно 36,3 и 70,4 кПа (272 и 528мм. рт. ст.).
Решение:
Согласно закону Дальтона парциальное давление данного газа прямо пропорционально его мольной доли на общее давление смеси газов:
где Р(смеси) – общее давление смеси; Р(А) – парциальное давление данного газа; (A) – мольная доля данного газа.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ: 34,02%NO; 65,98%CO.
Задача 44.
В закрытом сосуде вместимостью 0,6м3 находится при 0 °С смесь, состоящая из 0,2кг СО2, 0,4кг 02 и 0,15кг СН4. Вычислить: а) общее давление смеси; б) парциальное давление каждого из газов; в) процентный состав смеси по объему.
Решение:
Вычислим общее количество газов в смеси по уравнению:
, где
– количество газа, кмоль; m – масса газа, кг; М – молекулярная масса газа, кг/моль. Тогда:
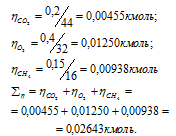
а) Общее давление смеси газов определяем по уравнению:
Тогда:
б) Парциальные давления газов рассчитываем по уравнению:
где Rk и k , соответственно, парциальное давление, и количество газа в смеси.
Тогда
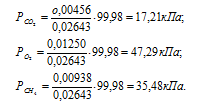
в) Парциальные объёмы газов рассчитаем по уравнению:
Тогда
Отношение парциальных (приведённых) объёмов отдельных газов к общему объёму смеси называется объёмной долей и определяется по формуле:
Тогда
Ответ:
Задача 45.
Газовая смесь приготовлена из 0,03м3 СН4, 0,04м3 Н2 и 0,01м3 СО. Исходные давления СН4, Н2 и СО составляли ответственно 96, 84 и 108,8 кПа (720, 630 и 816мм рт. ст.). Объем смеси равен 0,08м3. Определить парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём метана увеличился после смешения в 2,67 раза (0,08/0,03 = 2,67), объём водорода – в 2 раза (0,08/0,04 = 2), а объём угарного газа – в 8 раз (0,08/0,01 = 8). Во столько же раз уменьшились парциальные давления газов. Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ:
Задача 46.
В газометре над водой находятся 7,4л кислорода при 23 °С и давлении 104,1 кПа (781 мм. рт. ст.). Давление насыщенного водяного пара при 23 °С равно 2,8 кПа (21мм. рт. ст.). Какой объем займет находящийся в газометре кислород при нормальных условиях?
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:
Обозначив искомый объём через и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим:
где Р и V – давление и объём газа при температуре Т = 296К (273 +23 = 296); Р0 = 101,325кПа; Т0 = 273К; Р = 104,1кПа; – объём газа при н.у.
Ответ: V0 =6,825л.
Источник
Парциальное давление и объем
Содержание:
Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.
Смесь идеальных газов – это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.
При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие. Важный параметр любой такой смеси – так называемая весовая концентрация g i i -ного газа-компонента.
- N – количество газов, из которых состоит смесь;
- x i i -го газа – молярная концентрация указанного газа в составе смеси;
- ν i – количество молей i -го газа, присутствующего в смеси.
Понятие парциального давления
Парциальное давление – это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:
Парциальным называется давление p i , которое могло бы создаваться i -ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.
Формула парциального давления будет выглядеть так:
p i = m i μ i R T V = μ i R T V
Объем смеси здесь обозначен буквой V , ее температура – T .
Следует подчеркнуть, что поскольку средние кинетические энергии молекул смеси равны, то существует и равенство температур всех компонентов газовой смеси, находящейся в состоянии термодинамического равновесия.
Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона в следующей формулировке:
p = ∑ i = 1 N p i = R T V ∑ i = 1 N ν i
Исходя из него, мы можем выразить парциальное давление так:
Понятие парциального объема
У газовой смеси также есть такая характеристика, как парциальный объем.
Парциальный объем V i i -газа в газовой смеси – это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.
Если речь идет о смеси идеальных газов, то к ней применим закон Амага:
В самом деле, при выражении ν i из формулы выше у нас получится следующее:
ν i = p V i R T ; p = R T V p R T ∑ i = 1 N V i → V = ∑ i = 1 N V i
Для расчета парциального объема газа используется следующая формула:
Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона. Формула будет выглядеть так:
p V = m μ s m R T .
Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:
Здесь параметры R s m = R μ s m = R ∑ i = 1 N q i μ i означают удельную газовую постоянную смеси.
Условие: имеется сосуд объемом 1 м 3 , в котором находится 0 , 10 · 10 — 3 к г гелия и 0 , 5 · 10 — 3 к г водорода. Постоянная температура равна 290 К . Вычислите давление смеси и парциальное давление гелия в нем.
Начнем с вычисления количества молей каждого компонента смеси. Для этого можно использовать формулу:
Зная, что молярная масса водорода, согласно таблице Менделеева, составляет μ H 2 = 2 · 10 — 3 к г м о л ь , мы можем найти количество его молей в смеси по формуле:
ν H 2 = m H 2 μ H 2
Считаем, что получится:
ν H 2 = 0 , 5 · 10 — 3 2 · 10 — 3 = 0 , 25 ( м о л ь ) .
Точно такие же расчеты проводим и для гелия, зная, что μ H e = 4 · 10 — 3 к г м о л ь :
Теперь с помощью уравнения Менделеева-Клайперона можно найти парциальное давление каждого компонента:
Сначала рассчитаем давление водорода:
p H 2 V = ν H 2 R T → p H 2 = ν H 2 R T V
Парциальное давление будет равно:
p H 2 = 0 , 25 · 8 , 31 · 290 1 = 602 , 5 ( П а ) .
Теперь то же самое подсчитываем для гелия:
p H e = 0 , 025 · 8 , 31 · 290 1 = 60 , 25 ( П а ) .
Чтобы найти общее давление смеси газов, сложим сумму давлений ее составляющих:
p = p H 2 + p H e
Подставляем полученные ранее значения и находим нужный результат:
p = 602 , 5 + 60 , 25 = 662 , 75 ( П а ) .
Ответ: общее давление смеси составляет 662 , 75 П а , а парциальное давление гелия в смеси равно 60 , 25 П а .
Условие: дана смесь газов, состоящая из 1 к г углекислого газа и 0 , 5 к г O 2 . Если считать их идеальными, какой объем они будут занимать при давлении в 1 а т м ? Температура смеси равна 300 К .
Начнем с вычисления общей массы газовой смеси.
m = m O 2 + m C O 2
Значит, m = 1 + 0 , 5 = 1 , 5 .
Переходим к вычислению массовых компонентов смеси:
g O 2 = 0 , 5 1 , 5 = 0 , 33 ; g C O 2 = 1 1 , 5 = 0 , 67 .
Тогда газовая постоянная смеси будет равна:
R s m = R ∑ i = 1 N g i μ i
R s m = 8 , 31 0 , 33 32 · 10 — 3 + 0 , 67 46 · 10 — 3 = 200 Д ж к г К .
Объем смеси вычисляем с помощью уравнения Менделеева-Клайперона:
V s m = m s m R s m T s m p s m
Вспомнив, что по условию давление равно 1 а т м , что равно 10 5 П а , вычислим объем:
V s m = 1 , 5 · 200 · 300 10 5 = 0 , 9 м 3 .
Ответ: при указанных условиях смесь займет объем, равный 0 , 9 м 3 .
Источник
Давление газа на стенки сосуда. Закон Дальтона
Давление газа на стенки сосуда
Вследствие теплового движения частицы газа время от времени ударяются о стенки сосуда (рис.1,а). При каждом ударе молекулы действуют на стенку сосуда с некоторой силой. Складываясь друг другом, силы ударов отдельных частиц, образуют некоторую силу давления, постоянно действующую на стенку сосуда. Молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда (рис.1,б).
Рис.1. Давление газа на стенку сосуда: а) возникновение давления вследствие ударов о стенку хаотически движущихся частиц; б) сила давления как результат упругого удара частиц.
На практике чаще всего имеют дело не с чистым газом, а со смесью газов. Например, атмосферный воздух представляет собой смесь азота, кислорода, углекислого газа, водорода и других газов. Каждый из газов, входящих в состав смеси, вносит свой вклад в суммарное давление, которое оказывает смесь газов на стенки сосуда.
Закон Дальтона для газовой смеси
Для газовой смеси справедлив закон Дальтона:
давление газовой смеси равно сумме парциальных давлений каждого компонента смеси:
Рис.2. Закон Дальтона для газовой смеси
С точки зрения молекулярно-кинетической теории закон Дальтона выполняется потому, что взаимодействие между молекулами идеального газа пренебрежимо мало. Поэтому каждый газ оказывает на стенку сосуда давление, как если бы остальных газов в сосуде не было.
Источник
Задачи на нахождение парциального давления газов и общего давления смеси
Задача 41.
Смешивают 0,04м 3 азота, находящегося под давлением 96кПа (720мм. рт. ст.), с 0,02м 3 кислорода. Общий объем смеси 0,06м 3 , а общее давление 97,6кПа (732мм. рт. ст.). Каким было давление взятого кислорода?
Решение:
По условию задачи объём азота увеличился в 1,5 раза (0,06/0,04 = 1,5), а объём кислорода – в 3 раза (0,06/0,02 = 3). Во столько же раз уменьшились парциальные давления газов.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). Отсюда Исходя из того, что объём кислорода до смешения был в три раза больше, чем после смешения, рассчитаем давление кислорода до смешения:
Ответ: Робщ. = 100,8кПа.
Задача 42.
Газовая смесь приготовлена из 2л Н2 (Р = 93,3 кПа) и 5л CH4 (Р = 112 кПа). Объем смеси равен 7л. Найти парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём водорода увеличился в 3,5 раза (7/2 = 3,5), а объём метана – в 1,4 раза (7/5 = 1,4). Во столько же раз уменьшились парциальные давления газов.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Ответ:
Задача 43.
Газовая смесь состоит из NO и СО2. Вычислить объемное содержание газов в смеси (в %), если их парциальные давления равны соответственно 36,3 и 70,4 кПа (272 и 528мм. рт. ст.).
Решение:
Согласно закону Дальтона парциальное давление данного газа прямо пропорционально его мольной доли на общее давление смеси газов:
где Р(смеси) – общее давление смеси; Р(А) – парциальное давление данного газа;
(A) — мольная доля данного газа.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Ответ: 34,02%NO; 65,98%CO.
Задача 44.
В закрытом сосуде вместимостью 0,6м 3 находится при 0 °С смесь, состоящая из 0,2кг СО2, 0,4кг 02 и 0,15кг СН4. Вычислить: а) общее давление смеси; б) парциальное давление каждого из газов; в) процентный состав смеси по объему.
Решение:
Вычислим общее количество газов в смеси по уравнению:
, где
— количество газа, кмоль; m – масса газа, кг; М – молекулярная масса газа, кг/моль. Тогда:
а) Общее давление смеси газов определяем по уравнению:
где Rk и
k , соответственно, парциальное давление, и количество газа в смеси.
Отношение парциальных (приведённых) объёмов отдельных газов к общему объёму смеси называется объёмной долей и определяется по формуле:
Ответ:
Задача 45.
Газовая смесь приготовлена из 0,03м 3 СН4, 0,04м 3 Н2 и 0,01м 3 СО. Исходные давления СН4, Н2 и СО составляли ответственно 96, 84 и 108,8 кПа (720, 630 и 816мм рт. ст.). Объем смеси равен 0,08м 3 . Определить парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём метана увеличился после смешения в 2,67 раза (0,08/0,03 = 2,67), объём водорода – в 2 раза (0,08/0,04 = 2), а объём угарного газа – в 8 раз (0,08/0,01 = 8). Во столько же раз уменьшились парциальные давления газов. Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Ответ:
Задача 46.
В газометре над водой находятся 7,4л кислорода при 23 °С и давлении 104,1 кПа (781 мм. рт. ст.). Давление насыщенного водяного пара при 23 °С равно 2,8 кПа (21мм. рт. ст.). Какой объем займет находящийся в газометре кислород при нормальных условиях?
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:
Обозначив искомый объём через и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим:
где Р и V — давление и объём газа при температуре Т = 296К (273 +23 = 296); Р = 101,325кПа; Т = 273К; Р = 104,1кПа; — объём газа при н.у.
Ответ: V =6,825л.
Источник
Источник
