Сосуд усеченного конуса шарик угловая скорость
Задача по физике – 14543
Из танка, движущегося со скоростью $v = 70 км/ч$, стреляют по горизонтально летящему на высоте $H = 6 км$ самолету. Скорость самолета $u = 790 км/ч$, а ее направление совпадает с направлением движения танка. Определите угол вылета а снаряда относительно горизонта. Известно, что в момент выстрела самолет находился над танком, а снаряд попал в самолет в высшей точке траектории.
Подробнее
Задача по физике – 14544
В широком сосуде налита жидкость до высоты $H$. Через отверстие у дна сосуда жидкость начинает вытекать, причем ее скорость направлена под углом $alpha =60^{ circ }$ к горизонту (рис.). Определите высоту уровня жидкости в сосуде $H$, если известно, что струя поворачивается к земле в точке, расположенной на высоте $h = 15 см$ от дна сосуда.

Подробнее
Задача по физике – 14545
В сосуд, имеющий форму прямого усеченного конуса с радиусом основания $R = 10 см$, налита вода. Уровень воды находится на высоте $H = 10 см$ от дна сосуда. Определите силу давления воды на боковую поверхность сосуда. Образующая конуса составляет угол $alpha = 45^{ circ }$ с его высотой.
Подробнее
Задача по физике – 14546
Два груза, изготовленные из различных материалов с плотностями $p_{1} = 0,6 г/м^{3}$ и $p_{2} = 1,8 г/см^{3}$, связаны невесомой нитью и помещены в достаточно глубокий сосуд с водой. Определите отношение объемов грузов, при котором они будут плавать под поверхностью воды, не касаясь дна сосуда. Определите отношение натяжения ннтн к силе тяжести обоих тел. Плотность воды $rho = 1 г/см^{3}$.
Подробнее
Задача по физике – 14547
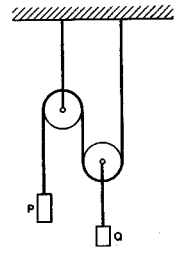
Грузы Р и Q находятся в равновесии с системой блоков (рис.). На груз Q кладут перегрузок массой $m = 0,2 кг$, и система приходит в движение. Определите силу давления перегрузка на груз Q. Масса груза Р $M = 0,3 кг$.
Подробнее
Задача по физике – 14548
На тело массой $m = 0,2 кг$ действует сила, изменяющаяся по закону $F = At$, где $A = 0,5 Н/с$. Определите ускорение и скорость груза через время $t = 2 с$ после начала движения.
Подробнее
Задача по физике – 14549
Два груза одинаковой массой $M$ соединены стержнем, масса которого $m$. Стержень может выдерживать максимальное натяжение $T_{max}$. Определите силу $F$, приложенную к одному из грузов, при которой произойдет разрыв стержня. Сила направлена параллельно плоскости. Коэффициент трения грузов о горизонтальную поверхность равен $mu$.
Подробнее
Задача по физике – 14550
Резиновый шнур длиной $l$ движется по шероховатой поверхности стола под действием силы $F$, приложенной к одному из его концов и направленной вдоль шнура. Пренебрегая удлинением резины, определите силу натяжения шнура в его сечении, отстоящем на расстоянии $b$ от точки приложения силы.
Подробнее
Задача по физике – 14551
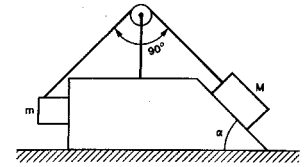
Два груза массами $m$ и $M$ связаны нерастяжнмой нитью, перекинутой через неподвижный блок (рис.). Коэффициент трения между грузами и гранями клина $mu = 0,2$. Угол наклона клина $alpha = 45^{ circ}$. Определите, при каком соотношении между массами грузов возможно равновесие системы. Массой нити и блока можно пренебречь.
Подробнее
Задача по физике – 14552
Прямоугольный клин массой $M = 4 кг$ покоится на горизонтальной плоскости. В некоторый момент времени на клин ставят два груза массами $m_{1} = 2 кг$ и $m_{2} = 1 кг$ (рис.). Определите ускорение клина. Трение между грузами и клином, а также между клином и плоскостью отсутствует. Угол $alpha = 30^{ circ}$.

Подробнее
Задача по физике – 14553
Небольшой шарик массой $m = 2 кг$ подвешен на нити. Шарик отвели в сторону так, что нить приняла горизонтальное положение, и отпустили. Определите угол между нитью и вертикалью, при котором нить оборвется. Нить выдерживает максимальное натяжение $T_{max} = 30 Н$. Ускорение свободного падения $g approx 10 м/с^{2}$.
Подробнее
Задача по физике – 14554
Два груза одинаковой массы, связанные невесомым стержнем, двигаются по окружностям в вертикальной плоскости вокруг общего центра О (рис.). Расстояние от центра О до одного из грузов $r = 10 см$, а до другого $R = 30 см$. Определите, с какой угловой скоростью стержень проходит положение равновесия, если наибольший угол отклонения стержня от вертикального направления $Omega = 60^{ circ}$.

Подробнее
Задача по физике – 14555
Система состоит из двух грузов массами $M = 200 г$ и $m = 50 г$. Грузы связаны между собой стержнем длиной $a = 40 см$. Такой же стержень соединяет груз массой $m$ с осью вращения АВ, расположенной вертикально (рис.). Все соединения шарнирные. Груз массой $M$ может скользить вдоль осевого стержня АВ, причем коэффициент трения $mu = 0,3$. Определите, при какой угловой скорости угол между каждым из стержней и осью вращения (стержнем АВ) $alpha = 45^{ circ}$.

Подробнее
Задача по физике – 14556
Тонкий стержень постоянного по длине сечения вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через его центр. Определите линейную скорость концов стержня, при которой произойдет его разрыв. Предел прочности на разрыв материала стержня $sigma = 2,5 cdot 10^{8} Н/м^{2}$, плотность материала стержня $rho = 8 г/см^{3}$.
Подробнее
Задача по физике – 14557
Проволочное кольцо радиусом $R = 20 см$ вращается вокруг вертикальной оси в горизонтальной плоскости. Ось проходит через центр кольца. Определите угловую скорость вращения $omega$, при которой произойдет разрыв кольца. Предел прочности на разрыв материала кольца $sigma = 10^{8} Н/м^{2}$, плотность материала $rho = 10^{4} кг/м^{3}$. Диаметр проволоки много меньше радиуса кольца.
Подробнее
Источник
Примеры решения задач
Задача 1.Тело бросили горизонтально с высоты 20 м. Найдите начальную скорость тела, если дальность полета равна 60 м.
Решение. В условии задачи высота представляет собой
проекцию перемещения на ось OY, т.е. Sy=20 м, дальность
полета – проекцию перемещения на ось OX, т.е. Sx=60 м.
Т.к. тело движется с постоянным ускорением, можно использовать уравнение
(1). Спроецировав уравнение (1)
на горизонтальную ось, получим (учитывая, что проекция вектора ускорения свободного падения на
данную ось равна нулю, т.е. gx=0):
(2)
В уравнении (2), кроме начальной скорости, неизвестно еще время. Его можно найти,
записав уравнение (1) в проекции на ось OY (учитывая, что проекция вектора
начальной скорости на данную ось равна нулю, т.е. v0y=0):
(3)
Из уравнения (3) выразим время
, и, подставив его
значение в уравнение (3), найдем начальную скорость:
.
Подставив численные значения, получим: v0=30 м/с.
Задача 2. Вентилятор вращается со скоростью, соответствующей частоте =900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал 100 оборотов.
Сколько времени прошло с момента выключения до остановки вентилятора?
Решение. > При каждом обороте вентилятор совершает угловое перемещение, равное рад. Следовательно, за n оборотов он совершит угловое перемещение
(4). Т.к. движение равнозамедленное, можно
использовать формулу для углового перемещения формулу (5) а модуль углового ускорения найти из
соотношения . Подставляя выражение для
углового ускорения в (5), с учетом (4) получим:
, откуда или
Задача 1. Найти силы натяжения нитей в устройстве с подвижным блоком, изображенного на рисунке. Масса
тел m1 = 4 кг, m2 = 3 кг. Массой нитей и блоков пренебречь.
 Решение. С учетом того, что двойной блок дает выигрыш в силе в два раза, а ускорение
Решение. С учетом того, что двойной блок дает выигрыш в силе в два раза, а ускорение
левого груза в раза больше (проигрыш в расстоянии), система уравнений в
векторной форме для каждого из грузов будет иметь вид:
или, в проекциях на координатную ось ОУ, направленную вверх:
.
Решая данную систему, получим выражение для ускорения:
Задача 2. Конус с углом раствора 2α вращается вокруг
вертикальной оси с угловой скоростью ω. В конусе находится шарик массой m,
прикрепленной к внутренней поверхности конуса с помощью нити. Радиус окружности,
по которой вращается шарик, равен R. Найти силу натяжения нити и силу давления шарика на
конус. Трение не учитывать.
 Решение. На шарик действуют сила тяжести, направленная вниз,
Решение. На шарик действуют сила тяжести, направленная вниз,
сила реакции опоры, направленная перпендикулярно внутренней поверхности конуса
и сила натяжения нити, направленная вдоль нити. Из-за вращения конуса шарик
описывает окружность радиуса R, соответственно
центростремительное ускорение направлено к центру данной окружности. Уравнение
второго закона Ньютона для данного случая имеет вид:
.
Спроецируем это уравнение на координатные оси, показанные на рисунке:
.
Из первого уравнения найдем силу
натяжения нити: , из второго – силу
реакции опоры, которая по модулю равна силе давления шарика на конус:
.
Задача 1. Какую силу надо приложить к латунной проволоке длиной 3 м и площадью сечения 1 мм2 для ее удлинения на 1,5 мм.
Решение. Связи силы с деформацией растяжения выражает закон Гука .
Коэффициент k можно найти, зная размеры проволоки и
значение модуля Юнга для латуни (это табличная величина, модуль Юнга Е=1011 Па).
Получаем: , F=50 Н.
Задача 2. Возле кольца из тонкой медной проволоки, радиусом r=1
мм, на его оси, на расстоянии l=5 см от центра кольца расположен шарик массой m=2 г.
Радиус кольца R=20 см. Найти силу, с которой кольцо притягивает шарик.
 Решение. Закон всемирного тяготения сформулирован для материальных
Решение. Закон всемирного тяготения сформулирован для материальных
точек. В данной задаче за материальную точку можно принять шарик, тогда как
кольцо необходимо разбить на отдельные элементы dliс массами
mi.
Возьмем точку, находящуюся, например, на вершине кольца. Шарик притягивается
этой точкой с силой , направленной, как показано
на рисунке. Если разложить элементарные силы Fi на составляющие, одна из которых параллельна оси
кольца, а вторая перпендикулярна, то перпендикулярные составляющие для любых
двух элементов, находящихся на противоположных концах диаметра, уничтожаются, а
параллельные составляющие складываются. Тогда сумма параллельных составляющих
, или
, или окончательно
. Вычисления дают
Задача 1. Шарик массой m упал с высоты h на стальную плиту и отскочил
вверх в результате абсолютно упругого удара. Найти изменение импульса шарика.
Решение. В задаче требуется найти изменение импульса (6)
Напомним, что изменение любой величины – это
разность между ее конечным и начальным значением). Из чертежа видно, что в момент
перед ударом импульс направлен вниз, а в момент после удара импульс направлен вверх.
Поэтому, спроецировав уравнение (6) на ось OY, получим:
Δp=p2+p1 (7)
Модуль импульса p1=mv1
найдем, применив закон сохранения механической энергии: на высоте h шарик
обладал потенциальной энергией mgh относительно поверхности плиты, в
момент удара потенциальная энергия полностью перешла в кинетическую mv2/2,
т.е. справедливо равенство
,
из которого найдем скорость шарика
.
Т.к. удар по условию абсолютно упругий, то после удара шарик поднимется на ту же высоту, следовательно,
скорость шарика после удара можно найти аналогично,
.
Подставив найденные значения в уравнение (7), получим ответ:
.
Задача 2. Пуля попадает в
ящик с песком и застревает в нем. Насколько сожмется пружина, удерживающая
ящик, если пуля имеет массу m, и движется со
скоростью v, а масса ящика с песком равна М, жесткость
пружины k.
 Решение. После соударения ящик вместе с пулей начинает двигаться с какой-то скоростью u, т.е.
Решение. После соударения ящик вместе с пулей начинает двигаться с какой-то скоростью u, т.е.
обладает кинетической энергией. Т.к. силой трения по условию задачи можно пренебречь, то будем считать, что вся
кинетическая энергия ящика с песком и пулей перейдет в потенциальную энергию
сжатой пружины, т.е.
, отсюда
.
Начальную скорость u можно найти, применяя закон сохранения импульса:
. Подставив значение
скорости в выражение для жесткости, окончательно получим:
.
Задача 1. Человек массой m=60 кг находится на неподвижной платформе,
массой M=100 кг. Какова будет частота вращения платформы n, человек будет двигаться
по окружности радиусом r=5 м вокруг оси вращения со скоростью v=4 км/ч относительно платформы.
Радиус платформы R=10 м. Считать платформу однородным диском, а человека точечной массой.
Решение: частота вращения связана с угловой скоростью соотношением
(8),
где- угловая скорость
платформы. Т.к. на платформу не действуют внешние силы, то выполняется закон
сохранения момента импульса: (9),
где угловая скорость человека ,
момент его инерции , момент инерции платформы
.
Подставим все значения в уравнение (9)
и выразим угловую скорость платформы: .
Подставив значение угловой скорости в (8), окончательно найдем:
,
численное значение
Задача 2. Груз массой m=2 кг привязан к концу шнура, намотанного на барабан радиусом
R=20 см. Груз опускается с ускорением a=3м/с2. Определите момент инерции барабана.
 Решение.
Решение.
Момент инерции барабана можно определить из основного уравнения вращательного
движения .
На барабан действует вращательный момент силы натяжения шнура
, т.е.
(10).
Модуль силы натяжения шнура, можно найти из уравнения второго закона Ньютона для груза, записанного в проекциях на
координатную ось, направленную вертикально вниз:
, отсюда
(11).
Угловое и тангенциальное ускорение, которое испытывают точки, лежащие на ободе барабана, связаны соотношением
(12).
Подставим (11) и (12) в (10)
и выразим момент инерции: .
Численное значение
Задача 1. Написать
уравнение гармонического колебательного движения, если известно, что амплитуда
колебаний равна 4 см, период – 2 с, а начальная фаза колебаний равна
.
Решение.
Уравнение гармонических колебаний имеет вид x = xm sin (ωt + φ0).
Циклическую частоту колебаний определим из соотношения
. Подставив данные в СИ в уравнение колебаний, получим ответ:
Задача 2.Уравнение незатухающих колебаний имеет вид:
Найти смещение от
положения равновесия точки, находящейся на расстоянии
y=2 м от источника колебаний через t=1 с после начала колебательного движения. Скорость
распространения колебаний v=150 м/с.
Решение. Уравнение волнового движения имеет вид .
Волновое число ,
подставим его в уравнение волны: или
. Расчеты дают х=9,4.10-3
м.
Источник
Исходный полный конус
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
- Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
- Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
- Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.
Существующие виды
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
- Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
- Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
- Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.
Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r2*h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Усеченный геометрический объект
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:
- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r12 + r22 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см2. При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r12 + pi*r22 = 4*pi*r22 + pi*r22 = 5*pi*r22.
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h2)^0,5 = (2,522 + 152 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см2.
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
Источник
