Сосуд в форме усеченного конуса
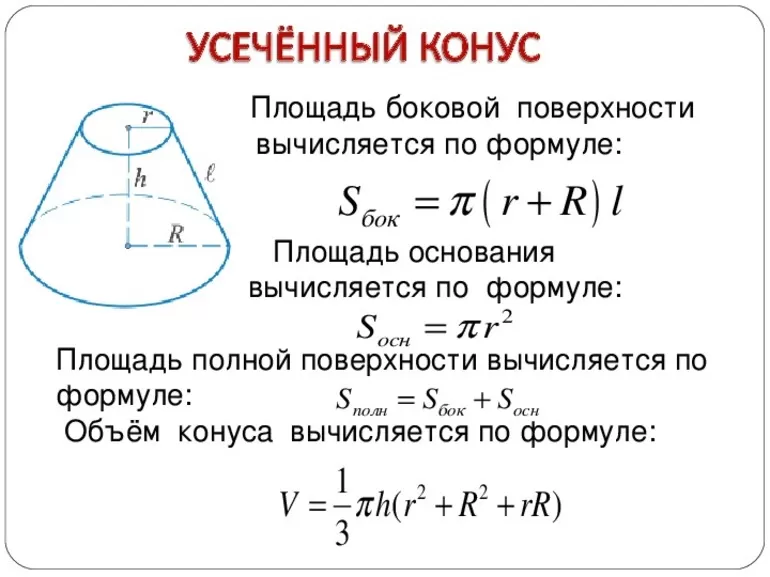
усеченный конус в быту
Альтернативные описания
• теплая ясная сухая летняя погода
• железная или деревянная посуда, с дужкой для ношения воды
• емкость для воды
• мера жидкостей, равная 1/40 части бочки или 20 бутылкам – около 12, 3 литров
• рыцарский шлем после конверсии
• цилиндрический сосуд с ручкой в виде дужки
• емкость для хранения жидких и сыпучих материалов и транспортировки их на небольшие расстояния
• русская мера жидкостей
• «Свой грех – с орех,а чужой – с …» (поговорка)
• «Не выбрасывай старое …, пока не убедишься, что новое не протекает»
• русская мера объема
• «пиво добро, да мало …» (посл.)
• эта емкость у пожарного обычно бывает конической
• оно было равно 10 кружкам, 16 винным и 20 водочным бутылкам, 100 чаркам, 200 шкаликам, 40 сороковкам
• эстонский композитор, автор опер «Каупо», «Либахунт», «Древний меч»
• эстонский композитор, автор симфонических произведений «Жаворонок», «В канун Иванова дня», «Птица Мидри»
• «сколько мусорное … не утрамбовывай – выносить все равно придется» (шутка)
• в первых российских кабаках минимальная тара при торговле на вынос была именно такой
• подвеска на коромысло
• шляпа того, у кого нос морковкой
• емкость на 10 литров с ручкой
• предмет, очень нужный там, где есть колодец
• усеченный конус для переноски жидкостей
• домашний мусоросборник
• шляпа для снеговика
• колодезная емкость
• клиент коромысла
• русская мера объема, равна 10 штофам, или 12,299 литра
• «лошадиная» норма воды
• головной убор снеговика
• с ним ходят по воду
• «в шахту спустился шахтер, принес воды во двор» (загадка)
• летняя сухая и ясная погода
• летняя сухая погода (народ.)
• емкость для мытья полов
• сосуд в колодце
• емкость
• емкость на коромысле
• мусорное … на кухне
• льет как из него
• «пиво добро, да мало …»
• пара к швабре в руках уборщицы
• что бросают в колодец?
• подвеска к коромыслу
• болтается на коромысле
• баба с ним, пустым, – к несчастью
• «шляпа» снеговика
• коромыслово-жестяная емкость
• хозяйственный сосуд
• «шапка» снеговика
• любая из подвесок на коромысле
• бросают в колодец, а потом достают
• «подвеска» на коромысле
• сосуд – ходить по воду
• «шляпа» снежной бабы
• русская мера объема воды
• невыносимая мужем емкость с мусором
• пара к швабре в руках поломойки
• бадья
• мера питья для лошади
• подвеска для коромысла
• гремит снаружи грузовика
• емкость уборщицы
• «стакан» для лошади
• ясная погода (устар.)
• емкость водоноса
• «каска» снеговика
• инвентарь пожарного щита
• сосуд для воды
• чем в колодец лазают?
• (разг.) ясная, солнечная, сухая погода
• Сосуд с ручкой в виде дужки
• Летняя сухая и ясная погода
• Сосуд с ручкой, используемый в хозяйстве
• Ёмкость, сосуд
• “Каска” снеговика
• “Лошадиная” норма воды
• “Пиво добро, да мало …”
• “Подвеска” на коромысле
• “Стакан” для лошади
• “Шапка” снеговика
• “Шапка” снежной бабы
• “Шляпа” снеговика
• “Шляпа” снежной бабы
• “Свой грех – с орех,а чужой – с …” (поговорка)
• арх. ведрие, ведренье ср. краснопогодье; ясная, тихая, сухая и вообще хорошая погода; противопол. ненастье. Не все ненастье, будет и ведро. После ненастья ведро. По ненастью ведро. Где гроза, тут и ведро. Отколе гроза, оттоле и ведро. После грозы ведро, после горя радость. Охотник ведра в тороках не возить. заказным ведром не далеко уедешь. дождь избы не кроют, а в ведро и сама не каплет. На сердце ненастье, так и в ведро дождь. То и счастье, что иному ведро, иному ненастье. По ненастью лыко драли, по ведру лапти плели, невпору. Ведреный, ведряный или ведрый, о погоде, сухой и ясный. Ветер за солнцем к ведреной погоде. Ведряный хлед, тамб. не овинный, сушеный на ветру. Ведреность, ведряность ж. свойство, состояние ведраго. Ведреть, ведренеть, о дне, погоде, становиться ведрым, проясняться. Погода выведрилась, разведрилась, поразведрилась. Маленько поведрело, проавдрело
• баба с ним, пустым, – к несчастью
• сосуд – ходить по воду
• ср. ведерко, ведерочко, ведрышко, ведерце; ведрище; деревянная обручная, а иногда и железная, кожаная посудина, с ушами и дужкою или перевеслом, для носки воды и др. жидкостей. обиходе, два ведра на коромысле должны быть в подъем женщине; казенное ведро, мepa жидкостей, фунтов перегонной воды; в анкерке три ведра, в бочке в ведре кружек штофов) или мерных бутылок. Во франц. гектометре
• чем в колодец лазают
• что бросают в колодец
• эстонский композитор, автор опер “Каупо”, “Либахунт”, “Древний меч”
• эстонский композитор, автор симфонических произведений “Жаворонок”, “В канун Иванова дня”, “Птица Мидри”
• “Не выбрасывай старое …, пока не убедишься, что новое не протекает”
• “пиво добро, да мало …” (посл.)
• “сколько мусорное … не утрамбовывай – выносить все равно придется” (шутка)
• “в шахту спустился шахтер, принес воды во двор” (загадка)
• ясная погода для русича
• «шапка» снежной бабы
• ёмкость на коромысле
Источник
Исходный полный конус
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
- Вершина – зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
- Коническая поверхность, образованная в результате перемещения отрезка – образующей, или генератрисы.
- Основание – часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.
Существующие виды
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
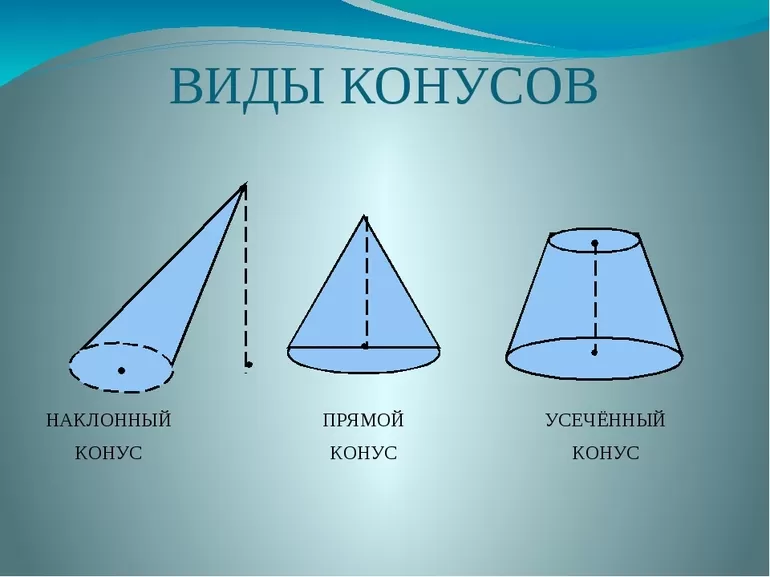
- Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
- Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
- Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина – высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.

Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r – радиус окружности в основании, g – длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
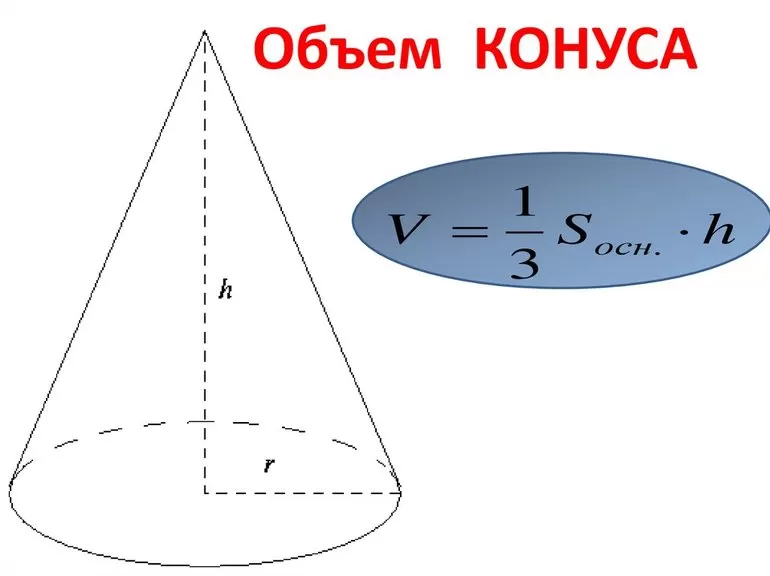
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r2*h. Здесь h – высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Усеченный геометрический объект
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
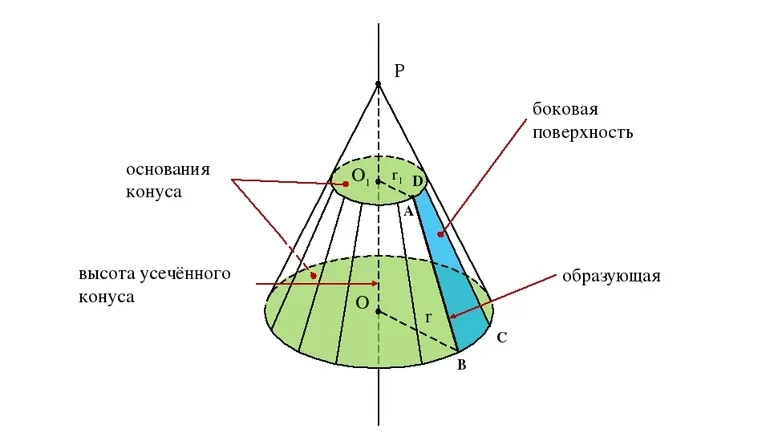
Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:

- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r12*H – 1/3*pi*r22*(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r12 + r22 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см2. При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r12 + pi*r22 = 4*pi*r22 + pi*r22 = 5*pi*r22.
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h2)^0,5 = (2,522 + 152 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см2.
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
Источник
Конусы
Рассмотрим произвольную плоскость α, точку S, не лежащую на плоскости α, и перпендикуляр SO, опущенный из точки S на плоскость α (точка O – основание перпендикуляра). Рассмотрим также произвольный круг с центром в точке O, лежащий на плоскости α.
Определение 1. Конусом называют фигуру, состоящую из всех отрезков, соединяющих точку S с точками указанного круга с центром в точке O, лежащего на плоскости α (рис. 1).



Рис.1
Определение 2.
Точку S называют вершиной конуса. | |
Отрезок SO называют осью конуса. | |
Расстояние от точки S до плоскостиРасстояние от точки S до плоскости α (длину отрезка SO) называют высотой конуса. | |
Круг с центром в точке O, лежащий на плоскости α, называют основанием конуса, радиус этого круга называют радиусом основания конуса, а саму плоскость α называют плоскостью основания конуса. | |
Отрезки, соединяющие точку S с точками окружности называют образующими конуса. | |
Совокупность всех образующих конуса составляет боковую поверхность конуса (коническую поверхность). | |
Полная поверхность конуса состоит из основания конуса и его боковой поверхности. |
Замечание 1. Отрезок SO часто называют высотой конуса.
Замечание 2. Все образующие конуса имеют одинаковую длину. У конуса с высотой h и радиусом основания r длина образующих равна
Усеченные конусы
Рассмотрим конус с вершиной S, осью SO, радиусом основания r и высотой h. Плоскость β, параллельная параллельная плоскости основания конуса и расположенная на расстоянии h1 от вершины расстоянии h1 от вершины S, пересекает конус по кругу радиуса r1 с центром в точке O1 (рис. 2).



Рис.2
Из подобия прямоугольных треугольников SOA и SO1A1 можно выразить радиус r1 через известные величины r, h и h1:
Таким образом, плоскость β делит конус на две части: конус с осью SO1 и радиусом основания r1, а также вторую часть, называемую усеченным конусом (рис. 3).



Рис.3
Усеченный конус ограничен двумя основаниями: кругом с центром в точке O радиуса r на плоскости α и кругом с центром в точке O1 радиуса r1 на плоскости β, а также боковой поверхностью усеченного конуса, которая представляет собой часть боковой поверхности исходного конуса, заключенную между плоскостями α и β. Полная поверхность усеченного конуса состоит из двух оснований усеченного конуса и его боковой поверхности. Часть каждой образующей исходного конуса, которая заключена между плоскостями α и β, называют образующей усеченного конуса. Например, на рисунке 3 одной из образующих усеченного конуса является отрезок AA1.
Высотой усеченного конуса называют расстояние между плоскостями расстояние между плоскостями оснований усеченного конуса. У усеченного конуса, изображенного на рисунке 2, высота равна h – h1.
Объем, площади боковой и полной поверхностей конуса и усеченного конуса
Введем следующие обозначения
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности конуса, а также формулы для вычисления объема, площади боковой и полной поверхности усеченного конуса.
| Фигура | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Конус |  | Sосн = πr2, Sбок= πrl, Sполн = πr2 + πrl, где r – радиус основания конуса, l – длина образующей конуса, h – высота конуса. |
| Усеченный конус |  | Sбок= π (r + r1)l , где h – высота усеченного конуса, r – радиус нижнего основания усеченного конуса, r1 – радиус верхнего основания усеченного конуса, l – длина образующей усеченного конуса. |
| Конус |
Формулы для объема, площади боковой и полной поверхности: Sосн = πr2, Sбок= πrl, Sполн = πr2 + πrl, где r – радиус основания конуса, l – длина образующей конуса, h – высота конуса. |
| Усеченный конус |
Формулы для объема, площади боковой и полной поверхности: , Sбок= π (r + r1)l , где h – высота усеченного конуса, r – радиус нижнего основания усеченного конуса, r1 – радиус верхнего основания усеченного конуса, l – длина образующей усеченного конуса. |
Замечание 3. Формула для вычисления объема конуса
может быть получена из формулы объема правильной n – угольной пирамиды
при помощи предельного перехода, когда число сторон правильной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
Замечание 4. Формула для вычисления объема усеченного конуса
может быть получена из формулы объема правильной усеченной n – угольной пирамиды
при помощи предельного перехода, когда число сторон правильной усеченной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Источник


