Сосуде лежит кусок льда

2011 год 109 вариант СЗ
В сосуде лежит кусок льда. Температура льда t1 = 0°С. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20°С? Тепловыми потерями на нагрев сосуда пренебречь.
(Решение)
2011 год. 01-2 вариант. С3
В бутылке объемом V = 1 л находится гелий при нормальном атмосферном давлении. Горлышко бутылки площадью S = 2 см2 заткнуто короткой пробкой, имеющей массу m = 20 г. Если бутылка лежит горизонтально, то для того, чтобы медленно вытащить из ее горлышка пробку, нужно приложить к пробке горизонтально направленную силу F = 1 Н. Бутылку поставили на стол вертикально горлышком вверх. Какое количество теплоты нужно сообщить гелию в бутылке для того, чтобы он выдавил пробку из горлышка? (Решение)
2011 год. 01-1 вариант. С3
Один моль идеального одноатомного газа переводят из состояния 1 с температурой Т1 = 300 К в состояние 2 таким образом, что в течение всего процесса давление газа возрастает прямо пропорционально его объему. В ходе этого процесса газ получает количество теплоты Q = 14958 Дж. Во сколько раз n уменьшается в результате этого процесса плотность газа? (Решение)
 2010 год. 11 вариант. С1
2010 год. 11 вариант. С1
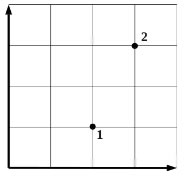
В кабинете физики проводились опыты с разреженным газом постоянной массы. По невнимательности ученик, отметив на графике начальное и конечное состояния газа (см. рисунок), не указал, какие две величины из трёх (давление р, объём V, температура Т) отложены по осям. В журнале осталась запись, согласно которой названные величины изменялись следующим образом: p1 < р2, V1 > V2, Τ1 < Ί2. Пользуясь этими данными, определите, какие величины были отложены на горизонтальной и вертикальной осях. Ответ поясните, указав, какие физические закономерности вы использовали. (Решение)
 2010 год
2010 год
304 вариант СЗ
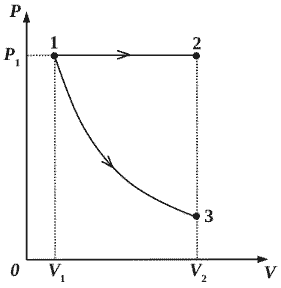
Некоторое количество одноатомного идеального газа расширяется из одного и
того же начального состояния (p1, V1) до одного и того же конечного объёма V2
первый раз по изобаре, а второй – по адиабате (см. рисунок). Отношение количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа |U3 — U1| на адиабате k = Q12/|U3 — U1| = 6 . Чему равно
отношение х работы газа на изобаре А12 к работе газа на адиабате А13? (Решение)
 2010 год. 135 вариант. С5
2010 год. 135 вариант. С5
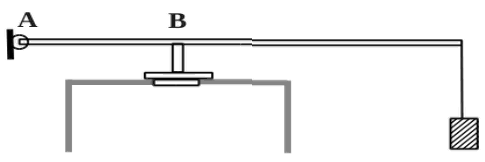
В цилиндр закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие площадью 5·10-4 м2, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии невесомым стержнем длиной 0,5 м, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). Расстояние АВ равно 0,1 м. К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через
580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите объём цилиндра. (Решение)
2009 год. 133 вариант. С1
В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
жидкости в сосуде? Ответ поясните. (Решение)
 2009 год. 133 вариант. С3
2009 год. 133 вариант. С3
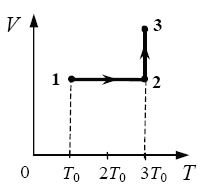
Один моль одноатомного идеального газа
переходит из состояния 1 в состояние 3 в
соответствии с графиком зависимости его объёма
V от температуры T (T0 = 100 К). На участке 2 − 3
к газу подводят 2,5 кДж теплоты. Найдите
отношение работы газа А123 ко всему количеству
подведенной к газу теплоты Q123. (Решение)
 2009 год. 304 вариант. С3
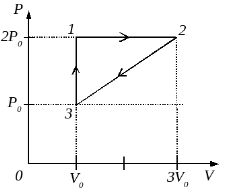
2009 год. 304 вариант. С3
Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты QH = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3?
(Решение)
 2008 год. 131 вариант. С2
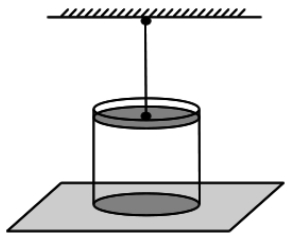
2008 год. 131 вариант. С2
Разогретый сосуд прикрыли поршнем, который с помощью вертикальной нерастяжимой нити соединили с потолком. На сколько процентов от начальной понизится температура воздуха в сосуде к моменту, когда сосуд оторвется от поверхности, на которой он расположен? Масса сосуда 5 кг. Поршень может скользить по стенкам сосуда без трения. Площадь дна сосуда 125 см2. Атмосферное давление 105 Па. Тепловым расширением сосуда и поршня пренебречь. (Решение)
2008 год. 5941 вариант. С2
В калориметре находился m1 = 1 кг льда при температуре t1 = -5°С. После добавления в калориметр m2 = 25 г воды в нем установилось тепловое равновесие при температуре t = 0°С. Какова температура t2 добавленной в калориметр воды, если в калориметре оказался в итоге только лёд? Теплоёмкостью калориметра пренебречь. (Решение)
2008 год. 05205939 вариант. С2
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз. На сколько градусов следует нагреть воздух в трубке, чтобы объём, занимаемый воздухом, стал прежним? Температура воздуха в лаборатории 300 К, а атмосферное давление составляет 750 мм рт.ст. (Решение)
 2008 год. 2 вариант. С2
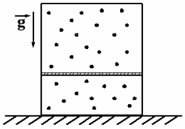
2008 год. 2 вариант. С2
Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество водорода при температуре 361 К. Какая масса газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь. (Решение)
2007 год. 19 вариант. С2
В сосуде находится одноатомный идеальный газ, масса которого 12 г, а молярная масса 0,004 кг/моль. Вначале давление в сосуде было равно 4•105 Па при температуре 400 К. После охлаждения газа давление понизилось до 2•105 Па. Какое количество теплоты отдал газ? (Решение)
2006 год. 61 вариант. С2
В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м3- мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
2006 год. 86 вариант. С2
Теплоизолированный сосуд объемом V = 2 м3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль гелия, а в другой – такое же количество молей аргона. Начальная температура гелия равна 300 К, а температура аргона 600 К. Определите давление смеси после удаления перегородки. Теплоемкостью сосуда пренебречь. (Решение)
2006 год. 33 вариант. С2
Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. При какой минимальной разности температур воздуха внутри шара и снаружи шар взлетит вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Оболочку шара считать нерастяжимой. (Решение)
2006 год. 222 вариант. С2
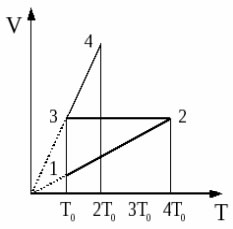
С одним молем идеального одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке в координатах V-Т. Во сколько раз количество теплоты, полученное газом в процессе 1-2-3-4, больше работы газа в этом процессе? (Решение)
 2005 год. 58 вариант. С2
2005 год. 58 вариант. С2
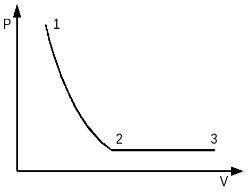
Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился при температуре T1 = 300 К. Затем газ изобарно нагрели, повысив температуру в 3 раза. Какое количество теплоты получил газ на участке 2-3? (Решение)
2004 год. 92 вариант. С2
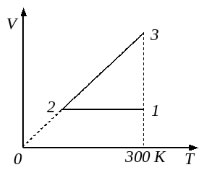
10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2-3? (Решение)
 2004 год. 77 вариант. С5
2004 год. 77 вариант. С5
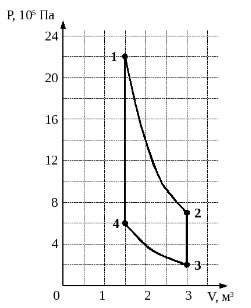
Идеальный одноатомный газ используется в качестве рабочего тела в тепловом двигателе. В ходе работы двигателя состояние газа изменяется в соответствии с циклом, состоящим из двух адиабат и двух изохор (см. рисунок). Вычислите КПД такого двигателя. (Решение)
2004 год. 49 вариант. С5
При электролизе воды образуется кислород О2 и водород Н2. Газы отводят в сосуд объёмом 100 л, поддерживая в нём температуру 300 К. Чему равна масса воды, которая разложилась в результате электролиза, чтобы суммарное давление в сосуде достигло 0,1 атм? Считать, что ничего не взрывается.
(Решение)
2004 год. 35 вариант. С5
Смесь одинаковых масс гелия, водорода и азота помещена в сосуд и нагрета до температуры 350 К. Плотность смеси оказалась равной 50 г/м3. Чему равно давление в сосуде? (Решение)
Источник
#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
Задачи, тесты
Е. М.
Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5,
8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где – объём погружённой части коробочки. Подставляя числовые данные, получаем
Отсюда глубина погружения коробочки равна
Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:
20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:
23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина
Решая совместно оба уравнения, получаем:
24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению:
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле полученной при решении задачи 9 (см. № 5/2010):
– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:
Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:
26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна
Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты
S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
