Сосуде находится система тел
Механика — квантовая физика. Расчётная задача
В. З. Шапиро
При решении расчётной задачи № 28 надо выделять следующие элементы:
- Работа с условием задачи: запись «Дано»,
- представление рисунка, если это необходимо для понимания физической ситуации;
- описание физической модели, т.е. указание на то, какие явления или процессы рассматриваются, какие закономерности можно использовать для решения задачи и чем можно пренебречь, чтобы ситуация отвечала выбранной модели.
- Запись всех необходимых для решения задачи законов и формул, описание используемых физических величин, которые не вошли в «Дано».
- Проведение математических преобразований и расчётов, получение ответа.
Задание № 28 оценивается в 2 балла, так как является типовой расчетной задачей.
1. Сталкиваются и слипаются два разных по массе пластилиновых шарика, причём векторы их скоростей непосредственно перед столкновением направлены навстречу друг другу и одинаковы по модулю: м/с. Во сколько раз масса тяжёлого шарика больше, чем лёгкого, если сразу после столкновения их скорость стала равной (по модулю) 0,5 м/с?
Необходимая теория:
Импульс
Дано:
м/с;
м/с
Найти:
Решение:
Сделаем чертеж, поясняющий условие задачи.
Применим закон сохранения импульса к системе двух взаимодействующих шаров.
Запись этого закона в векторной форме будет иметь вид:
(1), где – векторы скоростей первого и второго шаров до взаимодействия;
а и – векторы скоростей первого и второго шаров после взаимодействия.
Уравнение (1) в проекциях на выбранную ось ОХ будет иметь вид:
(2).
Здесь расставлены знаки проекций скоростей с учетом того, что первый шарик массой М движется по направлению оси ОХ, а второй шарик массой m движется противоположно оси ОХ. Кроме этого, сделано предположение, что после неупругого удара оба шарика будут двигаться по направлению оси ОХ. Это предположение основано на том, что масса левого шарика больше, чем правого, а модули скоростей до взаимодействия одинаковы.
Выразим из уравнения (2) отношение масс .
Подставим численные значения и проведем расчет.
Ответ: 3.
Секрет решения. При решении задач по теме «Закон сохранения импульса» необходимо соблюдать определенный алгоритм (последовательность действий):
- Записать закон сохранения импульса для системы взаимодействующих тел в векторном виде.
- Выбрать ось ОХ (или ОY), на которую надо спроецировать проекции тел до и после взаимодействия.
- Учесть вид взаимодействия (абсолютно упругий или абсолютно неупругий удар).
- Сделать предположение о движении тел после взаимодействия.
- Составить уравнение и решить его относительно неизвестной величины.
Этот алгоритм (последовательность действий) является необходимым инструментом при решении подобных задач. Вероятность того, что на ЕГЭ встретится точно такая же задача, очень мала. Особенно это справедливо для второй части. Только вооружившись данным методом решения задач, можно надеяться на успех.
2. Груз массой 120 кг удерживают с помощью рычага, приложив к его концу вертикально направленную силу 300 Н (см. рисунок). Рычаг состоит из шарнира без трения и длинного однородного стержня массой 30 кг. Расстояние от оси шарнира до точки подвеса груза равно 1 м. Определите длину стержня.
Необходимая теория:
Статика твёрдого тела
Дано:
М = 120 кг;
F = 300 Н;
m = 30 кг;
b = 1 м.
Найти: L – ?
Решение:
На рисунке отметим силы, приложенные к рычагу.
– сила тяжести стержня. С учетом того, что стержень однородный, центр тяжести расположен посередине.
– сила реакции, действующая со стороны опоры на стержень.
– вес груза массой М, который действует на стержень.
Для рычага, находящегося в равновесии, алгебраическая сумма моментов сил равна нулю.
Рассмотрим моменты сил относительно точки опоры.
Момент силы реакции опоры равен нулю, так как плечо этой силы относительно точки опоры равно нулю.
Будем считать моменты сил, вращающих рычаг против часовой стрелки, положительными, а моменты сил, вращающих рычаг по часовой стрелке, отрицательными.
Тогда
Составим уравнение:
Решим это уравнение относительно L.
Подставим численные значения и проведем расчет.
(м).
Ответ: 4 м.
Секрет решения. Решение подобных задач сводится к составлению уравнений, выражающих условия равновесия тел.
Первое условие: векторная сумма сил, приложенных к телу, равна нулю.
Второе условие: алгебраическая сумма моментов сил, приложенных к телу, равна нулю.
Сложности в этой теме связаны с определением плеч сил. Надо помнить, что плечо – это кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила.
Если в задаче дается тело, находящееся на двух опорах, то, возможно, потребуется составление условия равновесия через моменты сил для двух точек С и D опоры (рис. 1)
Рис.1
Главное, надо помнить, что для решения системы уравнений необходимо, чтобы число неизвестных было равно числу независимых уравнений.
3. Два груза подвешены на достаточно длинной невесомой нерастяжимой нити, перекинутой через идеальный блок (см. рисунок). Грузы удерживали неподвижно, а затем осторожно отпустили, после чего они начали двигаться равноускорено. Опустившись на 2 м, левый груз приобрёл скорость 4 м/с. Определите силу натяжения нити, если масса правого груза m = 1 кг. Трением пренебречь.
Необходимая теория:
Второй и третий законы Ньютона
Дано:
m = 1 кг;
h = 2 м;
v = 4 м/с.
Найти: Т-?
Решение:
Укажем все силы, которые действуют на грузы массой М и m.
– сила тяжести, действующая на груз массой М.
– сила тяжести, действующая на груз массой m.
– сила натяжения нити, действующая на груз массой М.
– сила натяжения нити, действующая на груз массой m.
Составим уравнение движения для каждого груза на основании второго закона Ньютона:
Запишем эти уравнения в проекциях на ось OY.
Так как нить невесома и нерастяжима, а блок идеальный, то
и
Тогда уравнения (1) и (2) примут вид:
(3);
(4).
Для нахождения силы натяжения нити достаточно воспользоваться уравнением под номером 4. Из него можно выразить силу натяжения нити Т.
(5).
Из кинематической формулы с учетом равенства нулю начальной скорости найдем ускорение системы тел.
так как s = h.
Подставив ускорение в формулу (5), получим:
Проведем расчет силы натяжения нити:
Н.
Ответ: 14 Н.
Секрет решения. При решении задач по темам «Движение связанных тел», «Движение тел по наклонной плоскости» необходимо использовать следующий алгоритм (последовательность действий):
- Указать на чертеже (рисунке) все силы, приложенные к каждому телу.
- Составить уравнение движения для каждого тела в векторном виде на основе второго закона Ньютона.
- Выбрать оси координат ОХ и ОY и записать уравнения движения в проекциях на выбранные оси.
- Составить систему уравнений и решить ее относительно неизвестной величины.
- Подставить численные значения и провести расчет.
Иногда, при использовании этого алгоритма, возникает вопрос о направлении осей ОХ и ОY, куда направить «стрелочки», вверх-вниз, вправо-влево? Это не имеет никакого значения, больше того, для одного тела направление оси можно выбрать вверх, а для другого вниз. Это равносильно тому, что математическое уравнение можно умножить (разделить) на (-1), от этого равенство не изменится.
Источник
При работе со своими учениками, у меня накапливается много задач. Поэтому я публикую разборы задач в свободный доступ, стараюсь делать это максимально подробно и понятно, чтобы начинающие могли прочитать и разобраться в нужной для них теме. Ну а за подробными индивидуальными консультациями и репетиторством вы можете написать в мою группу в вк или в личные сообщения. Также большое количество разборов задач вы сможете найти в моей группе Репетитор IT mentor
Задача 1. На тело массой 100 кг, лежащее на наклонной плоскости, которая образует с горизонтом угол 40°, действует горизонтальная сила 1500 Н. Определить:
1) силу, прижимающую тело к плоскости;
2) силу трения тела о плоскость;
3) ускорение, с которым поднимается тело. Коэффициент трения k = 0.10; g = 10м/с².
Задача 2. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Найти ускорение тела, если на него действует сила тяжести P, а коэффициент трения между телом и плоскостью равен k . При какой величине силы F движение будет равномерным.
Задача 3. Два шара массами m1 = 2.5 кг и m2 = 1.5 кг движутся навстречу друг другу со скоростями v1 = 6 м/c и v2 = 2 м/c . Определить: 1) скорости шаров после удара; 2) кинетические энергии шаров до и после удара; 3)энергию, затраченную на деформацию шаров при ударе. Удар считать прямым, неупругим.
Прикрепляю очередной разбор задачи по физике по теме закона сохранения импульса. Неупругие шары после удара не восстанавливают свою первоначальную форму. Таким образом, сил, которые отталкивали бы шары друг от друга, не возникает. Это значит, что после удара шары будут двигаться вместе (слипшись) с одной и той же скоростью . Эту скорость определим по закону сохранения импульса. Так как шары двигаются по одной прямой, то можно записать импульс системы до удара и после удара. Считаем, что в задаче не действует диссипативных сил (сил трения, сопротивления воздуха и т.д.), поэтому импульс вдоль оси Ox сохраняется, тогда (смотри решение на картинке). Расписал довольно подробно, но если что-то не будет понятно, то задавайте вопросы в комментариях.
Задача 4. Диск массой m, радиус которого R , вращается с угловой скоростью ω0 вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. После прекращения действия на него силы диск останавливается в течение времени t. Определить угловое ускорение диска и тормозящий момент, действующий на него.
Задача 5. Два тела массами m1 и m2 связаны нитью, перекинутой через блок массой M . Найти ускорение тел, считая блок сплошным диском.
Задача 6. Шар катится по горизонтальной поверхности со скоростью v . На какую высоту h относительно своего первоначального положения поднимется шар, если он начнет вкатываться на наклонную плоскость без проскальзывания?
Задача 7. На краю вращающейся с угловой скоростью ω0 платформе стоит человек массой m. После того, как человек перешёл в другую точку платформы, угловая скорость её вращения стала равной ω. Найти расстояние от оси вращения до человека, считая платформу диском массой M и радиусом R.
Задача 8. Тело массой m брошено со скоростью v0 под углом α к горизонту. Найти кинетическую и потенциальную энергию тела в высшей точке траектории.
Задача 9. На горизонтальной поверхности находятся два тела массами m1 = 10 кг и m2 =15 кг, связанные нитью. К телу массой m2 прикладывают силу F = 100 Н, направленную под углом α = 60° к горизонту. Определить ускорение грузов и силу натяжения нити, соединяющей грузы. Трением пренебречь. (обязательно указать все силы на чертеже!)
Задача 10. На поверхности стола лежит груз массой m2 = 2 кг. На нити, прикрепленной к грузу m2 и перекинутой через невесомый блок, подвешен груз m1 = 1 кг. Коэффициент трения груза о поверхность стола 0,2. Найти ускорение грузов и силу натяжения нити.
Задача 11. Лодка массой 200 кг и длиной 3 м стоит неподвижно в стоячей воде. Мальчик массой 40 кг в лодке переходит с носа на корму. Определите, на какое расстояние при этом сдвинется лодка.
Считаем, что в нашей задаче не действует внешних сил, поэтому по теореме о центре массы системы грузов, можно считать, что координаты центра масс сохраняются в проекциях на ось OX (по оси OY движения не происходит). Проведем ось Y(ноль оси X) через центр лодки, тогда можно записать координаты человека и лодки до перехода человека с носа на корму.
Задача 12. Шарик массой 5 кг подвешен на нити. Нить может выдержать максимальное натяжение 100 Н. На какой минимальный угол от положения равновесия нужно отклонить нить с шариком, чтобы он оборвал нить, проходя через положение равновесия? (обязательно сделать рисунок, указать действующие силы!)
Задача 13. Два неупругих шара массами m1=2 кг и m2=3 кг движутся со скоростями соответственно v1=8 м/c и v2=4м/с. Определить количество теплоты, выделившееся при их столкновении. Рассмотреть 2 случая: 1) шары движутся навстречу друг другу; 2) меньший шар догоняет больший.
Задача 14. Тело совершает гармонические колебания по закону x(t) = 50⋅sin(π/3⋅t) (см). Определить полную энергию тела, если его масса 0,2 кг. Какая сила действует на тело в момент времени t = 0,5 с?
Задача 15. Два математических маятника, длины которых отличаются на Δℓ =16 см, совершают за одно и то же время: один − 10 колебаний, другой − 6 колебаний. Определить длины маятников.
Задача 16. Определить, сколько молей и молекул водорода содержится в объёме V = 5 м³ под давлением Р = 767 мм.рт.ст. при температуре t = 18 ° С. Какова плотность газа?
Задача 17. Сколько кислорода выпустили из баллона ёмкостью 1 дм3, если давление его изменилось от 14 атм до 7 атм, а температура от 27°С до 7 °С ?
Задача 18. В сосуде объёмом V = 2 м³ находится смесь m1 = 4 кг гелия и m2 = 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
Задача 19. В сосуде содержится смесь газов: гелия массой 12 г и водорода массой 2 г, температура в сосуде 77°С, давление 20 кПа. Определить молярную массу и плотность смеси газов.
Задача 20. Гелий массой 20 г нагрели от 100°С до 400°С, причем газу была передана теплота 30 кДж. Найти изменение внутренней энергии гелия и совершенную им работу.
Задача 21. При изотермическом расширении от 0,1 м3 трех молей газа его давление меняется от 4,48 атм до 1 атм. Найти совершаемую при этом работу и температуру, при которой протекает процесс.
Задача 22. Моль идеального газа, имевший первоначально температуру 300ºК, расширяется изобарически до тех пор, пока его объем не возрастет в 3 раза. Затем газ охлаждается изохорически до первоначальной температуры. Определить суммарное получаемое газом количество теплоты. Обязательно нарисовать графики процессов.
Задача 23. Азот массой m = 1 кг занимает при температуре Т1 = 300 К объём V = 0,5 м³. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определить конечный объём газа и конечную температуру.
Задача 24. Газ расширяется адиабатически, причём объём его увеличивается вдвое, а термодинамическая температура падает в 1,32 раза. Какое число степеней свободы i имеют молекулы этого газа?
Задача 25. Баллон ёмкостью V = 20 л с кислородом при давлении Р = 107 Па и температуре t1 = 70 ºС нагревается до температуры t2 = 270 ºС. Какое количество теплоты при этом поглощает газ?
Задача 26. Азот, занимающий при давлении, равном Р1 = 10⁵ Па объём V1 = 10 л, расширяется вдвое. Найти конечное давление и работу, совершённую газом в процессах: а) изобарном; б) изотермическом; в) адиабатном.
Задача 27. Кислород, масса которого 200 г, нагревают от температуры Т1 =300 К до Т2 = 400 К. Найти изменение энтропии, если известно, что начальное и конечное давление газа одинаковы и близки к атмосферному.
Задача 28. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 1,5∙10⁵ Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 260 К. Найти КПД машины, количество теплоты Q1, получаемое машиной за один цикл от нагревателя, и количество теплоты Q2, отдаваемое за один цикл холодильнику.
Задача 29. Найти суммарную кинетическую энергию Е поступательного движения всех молекул, содержащихся в объёме V = 1 дм³ газа при атмосферном давлении.
Задача 30. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 100 г водорода при температуре 400 К ? Чему равна полная внутренняя энергия газа?
Спасибо, что дочитали до конца, дорогие подписчики 🙂 Если вам интересен подобный контент и разборы задач, то оставляйте обратную связь в виде лайков и комментариев.
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в Telegram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Источник
29. Механика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
К стенке стакана с водой привязан алюминиевый шар массой (m=3) кг. Нить образует со стенкой сосуда угол (alpha=30^circ). Найдите силу натяжения нити. Ответ дайте в Ньютонах. 
Запишем второй закон Ньютона на ось (y) [F_text{ А}-mg +Tcos alpha =0 quad (1)] С учетом того, что сила Архимеда равна [F_text{ А} = rho_0 g V=rho_0 g dfrac{m}{rho} quad (2)] (rho_0) – плотность жидкости, (V) – объем погруженной части тела, (rho) – плотность алюминия.
Выразим из (1) силу натяжения нити (T), с учетом (2) [T=dfrac{mg-dfrac{rho_0 g m}{rho}}{cos alpha }=dfrac{mg(rho -rho_0)}{rhocos alpha }=dfrac{30text{ Н}(2700 text{ кг/м$^3$}-1000text{ кг/м$^3$})}{2700 text{ кг/м$^3$}cdot dfrac{sqrt{3}}{2}}=22text{ Н}]
Ответ: 22
Ко дну сосуда с водой площадью (S=100) см(^2) привязан деревянный шар, при этом нить натягивается и действует на шар с силой (T). Если перерезать нить, то шар всплывет, а уровень жидкости изменится на (h=20) см. Найдите силу натяжения нити. Ответ дайте в Н.
Пусть (rho) – плотность жидкости, (H) – первоначальный уровень воды, тогда после перерезания нити уровень уменьшится на (h). Значит гидростатическое давление до перерезания нити [P_1=rho g H] но так как есть еще сила натяжения нити, которая удерживает шар в воде, но не действует на дно, то сила давления на дно равна [F_1=rho cdot g cdot H cdot S -T] Во втором случае нить обрывается и шар всплывает и уровень уменьшается на (h), тогда сила давления на дно будет равна [F_2=rho cdot g cdot (H-h)cdot S] Поскольку масса щара и воды остается неизменным, то и сила давления на дно при равновесных состояниях остается неизменной, а значит мы можем приравнять (F_1) и (F_2) [rho cdot g cdot H cdot S -T=rho cdot gcdot H cdot S -rho cdot gcdot h cdot S] Выразим силу натяжения нити [T=rho cdot gcdot h cdot S=1000 text{ кг/м$^3$}cdot 10text{ Н/кг} cdot 0,2text{ м}cdot 0,01text{ м$^2$}=20text{ Н}]
Ответ: 20
Стержень согнули под прямым углом с соотношением полученных сторон 2:3 и подвесили нить, привязанную к точке сгиба. Найдите массу груза, который надо прикрепить к концу короткой стороны, чтобы концы сторон находились на одном уровне, если масса стержня 600 г. Ответ дайте в граммах.
Запишем правило моментов относительно оси подвеса. [dfrac{3}{5}m_1g dfrac{3l}{10}cos alpha -dfrac{2}{5}m_1gdfrac{l}{5}sin alpha – m_2 dfrac{2l}{5}cos alpha =0] где (l) – длина стержня, (m_1) – его масса. (Здесь берется (dfrac{3l}{10}) в первом случае, так как центр тяжести однородного стержня находится в середине, а у нас эта сторона равна (dfrac{3l}{5}), а половина (dfrac{3l}{10}), точно также и для второго слагаемого) Выразим отсюда массу грузика [m_2=dfrac{m_1}{20}(9ctg alpha -4)] так как отношение сторон 2:3, то (ctg alpha =1,5) А значит [m_2=dfrac{9,5m_1}{20}=285text{ г}]
Ответ: 285
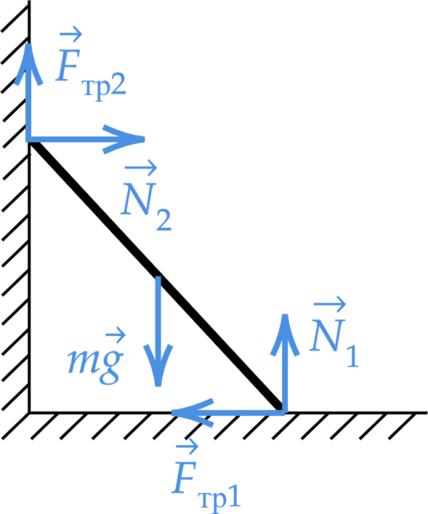
К вертикальной стенке прислонена однородная доска, образующая с горизонтальным полом угол (alpha=45^circ) Коэффициент трения доски об пол равен (mu=0,4) Каков должен быть коэффициент трения доски о стену, чтобы доска оставалась в равновесии?
Запишем второй закон Ньютона и правило моментов относительно центра доски, с учетом того, что доска покоится [begin{cases}
mg-N_1-F_text{ тр2}=0\
N_2-F_text{ тр1}=0 quad (1)\
(F_text{ тр1}+ N_2 )dfrac{l}{2}sin alpha + F_text{ тр2}dfrac{l}{2}cos alpha-N_1 dfrac{l}{2}cos alpha =0 quad (2)\
end{cases}] Так как (F_text{ тр1}=mu N_1), а (F_text{ тр2}=mu_2 N_2) и с учетом (1) уравнение (2) можно переписать в виде [2mu N_1 sin alpha + mu_2 mu N_1 cos alpha =N_1 cos alpha] Отсюда (mu_2) [mu_2 =dfrac{N_1 cos alpha – 2mu N_1 sin alpha }{mu N_1 cos alpha }=dfrac{1}{mu} -2 tg alpha =dfrac{1}{0,4}-2cdot 1=0,5]
Ответ: 0,5
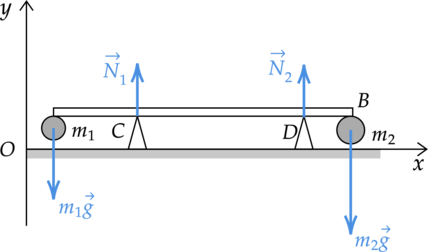
Два небольших шара массами (m_1 = 0,2) кг и (m_2 = 0,3) кг закреплены на концах невесомого стержня (AB), расположенного горизонтально на опорах (C )и (D) (см. рисунок). Расстояние между опорами (l = 0,6) м, а расстояние (AC) равно 0,2 м. Чему равна длина стержня (L), если сила давления стержня на опору (D) в 2 раза больше, чем на опору (C)? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень — шары».
Источник: Демонстрационная версия ЕГЭ – 2020 по физике.
На твердое тело, образованное двумя шарами и стержнем действует силы тяжести первого и второго шаров (m_1 g)и (m_2g), а также силы реакции опоры (N_1) и (N_2). По условию (2N_1=N_2) Запишем второй закон Ньютона и правило моментов относительно точки А. [begin{cases}
N_1 +N_2 -m_1g -m_2 g=0\
N_1 x +N_2 (l+x)-m_2 g L=0\
end{cases}] где (x) – AC и плечо силы (N_1). Так как (N_2=2N_1), то систему уравнений можно переписать в виде [begin{cases}
3N_1 =g(m_1 +m_2)\
N_1 x +2N_1 (l+x)=m_2 g L\
end{cases}] Поделим второе уравнение на первое [x+dfrac{2l}{3}=Ldfrac{m_2}{m_1+m_2}] Отсюда длина стержня [L=dfrac{m_2+m_1}{m_2}left(x+dfrac{2l}{3}right)=dfrac{0,3text{ кг}+0,2text{ кг}}{0,3text{ кг}}left(0,2text{ м}+ dfrac{2cdot 0,6 text{ м}}{3}right)=1text{ м}]
Ответ: 1
Вертикальная труба с поршнем, плотно прилегающим к ее внутренним стенкам, опущена нижним концом в воду. Вначале поршень находился в самом нижнем положении, на уровне воды, а затем его медленно поднимают на высоту 20 м. Пренебрегая трением, найдите совершенную при этом работу (в кДж). Площадь поршня 100 см(^2). Атмосферное давление 100 кПа.
Процесс поднятия поршня происходит в 2 этапа. Первый этап: давление под поршнем будет положительным и равное [p_0-rho g h] где (rho) – плотность воды, (h) – высота подъезда поршня.
Вода будет заполнять весь объем под поршнем, а приложенная к поршню сила будет компенсировать давление внутри, она будет равна [F=rho g h S] Она будет линейно возрастать. Это будет до момента, пока вода не поднимется на высоту, равную [h_0=dfrac{p_0}{rho g}=dfrac{100text{ кПа}}{1000text{ кг/м$^3$} cdot 10 Н/кг}=10text{ м}] При подъеме поршня на высоту (h_0) давление станет равным нулю. После этого вода перестает подниматься, а сила, приложенная к поршню, остается равной [F’=rho g h_0 S=p_0S] Работа по поднятию равна сумме работ: работе по поднятию до высоты (h_0) (A_0=dfrac{0+F_1}{2}h_0=dfrac{p_o S h_0}{2}) (так как она линейно возрастает, то берем как среднее арифметическое от начального, до конечного) и работе по поднятию от высоты (h_0) и конечной высоты (A_1=F_1(h_1-h_0)=p_o Sh_1-p_o Sh_0). Значит, полная работа равна [A=dfrac{p_o S h_0}{2}+ p_0 S h_1 -p_0 Sh_0=p_0 S left(h_1 -dfrac{h_0}{2})=100text{ кПа}cdot 10^{-2}text{ м$^2$}(20text{ м}-5text{ м}right)=15text{ кДж}]
Ответ: 15
В гладкий высокий стакан радиусом 4 см поставили однородную алюминиевую палочку длиной 10 см и массой 0,9 г, после чего в стакан налили до высоты h = 4 см воду. Найдите модуль силы (F), с которой верхний конец палочки давит на стенку стакана. Сделайте рисунок с указанием сил, действующих на палочку. Ответ дайте в мН.
1. Найдем высоту палочки, относительно дна стакана [H=sqrt{l^2-4R^2}=sqrt{0,01text{ м$^2$}-4cdot 0,0016text{ м$^2$}}=0,06text{ м}] где (l) – длина палочки, (R) – радиус стакана.
2. Сделаем рисунок с изображением всех сил, действующих на палочку.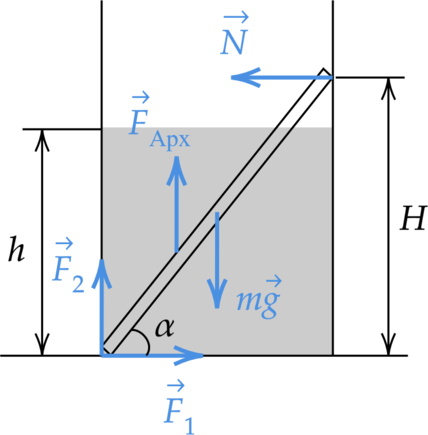 
3. Найдем силу Архимеда, действующую на палочку. Палочка погружена в жидкость на (dfrac{h}{H}) от своего объема, то есть [F_text{ Арх}=rho_text{ж}gleft(dfrac{h}{H}V right)=dfrac{rho_text{ж}}{rho}dfrac{mgh}{H }] где (V) – объем тела, (rho) – плотность палочки, (rho_text{ж}) – плотность жидкости.
4. Запишем правило моментов, относительно оси, проходящей перпендикулярно рисунку через точку приложения сил (F_2) и (F_1). [mgdfrac{l}{2} cos alpha -F_text{арх}left(dfrac{l}{4}cos alpha right)-Nlsin alpha =0] Преобразуем [mgR-F_text{арх}left(dfrac{h}{2}ctg alpharight)-NH=0] Выразим силу реакции опоры. С учетом третьего закона Ньютона она будет равна силе давления палки на стенку сосуда. [N=mgdfrac{R}{H}-F_text{арх}left(dfrac{h}{2H}ctg alpharight)=mgdfrac{R}{H}left( 1-dfrac{rho_text{ж}}{rho}left(dfrac{h}{H}right)^2right)=] [F=N=0,0009text{ кг}cdot 10text{ Н/кг}dfrac{0,04text{ м}}{0,06text{ м}}left( 1-dfrac{1000text{ кг/м$^3$}}{2700text{ кг/м$^3$}}left( dfrac{0,04text{ м}}{0,06text{ м}}right)^2 right)approx 5cdot 10^{-3}text{ Н}]
Ответ: 5
Источник