Столкновение частиц идеального газа со стенкой сосуда
Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.
Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма – частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.
Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера 1 ат = 9,81-104 Па;
физическая атмосфера 1 атм = 1,013-105 Па;
миллиметры ртутного столба 1 мм рт. ст.= 133 Па;
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.
Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.
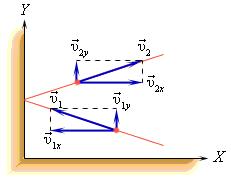
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.
Приборы, измеряющие давление, называют манометрами. Манометры фиксируют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.
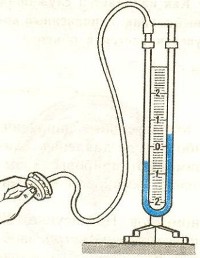
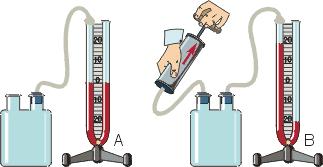
Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый – для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

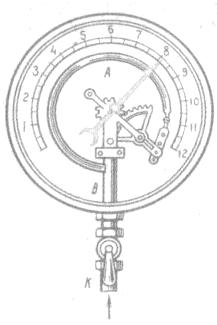
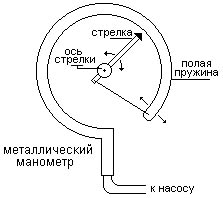
Металлический манометр – для измерения больших давлений.

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.
Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
p = 1/3·m0·n·v2
m0 – масса одной молекулы газа;
n = N/V – число молекул в единице объема, или концентрация молекул;
v2 – средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
Так как m0·n = m0·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v2
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
p = nkT
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
![]()
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим ![]() или
или ![]()
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
![]()
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
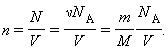
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
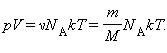
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
Соотношение
![]()
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
Источник
Говоря об идеальном газе, мы исходили из того, что молекулы не взаимодействуют между собой. На самом деле предполагалось, конечно, отсутствие потенциальной энергии взаимодействия между ними. Упругие столкновения между молекулами и молекул со стенками обязательно должны происходить хотя бы потому, что иначе будет отсутствовать механизм, с помощью которого устанавливается равное распределение энергии по степеням свободы, иначе нельзя будет говорить о температуре системы, давлении в ней и т. п. Столкновения молекул происходят случайно. Они приводят к изменению направления и величины скорости частиц, но не меняют распределения молекул по скоростям и координатам в равновесных системах.
Возникает вопрос: а всегда ли молекулы будут сталкиваться друг с другом? Ведь молекулы очень малы, а расстояния между ними в идеальном газе на порядок больше их линейных размеров. Быть может, для сосудов малых размеров они летят без соударений от стенки к стенке? Подсчитаем, сколько раз в единицу времени одна молекула может столкнуться с другими и какое расстояние она пролетает в среднем между столкновениями.
Прежде чем перейти к вычислениям, примем простейшую модель для молекул. Будем представлять их в виде упругих шариков. При столкновении молекул с эффективными диаметрами d1 и d2 их центры сближаются на расстояние (d1 + d2)/2 (рис. 4.2).

Рис. 4.2. Столкновение двух молекул (1) и траектория движения выделенной молекулы газа (2): направление ее движения меняется, когда какая-то из молекул среды попадает в радиус взаимодействия R = (dt + d2)/2
Если представить себе, что молекула 1 налетает на молекулу 2, то столкновение произойдет; если первая молекула попадет в сферу радиусом
описанную вокруг второй молекулы. Площадь сечения этой сферы
Величина R называется эффективным радиусом взаимодействия молекул1 и 2, а — эффективным сечением взаимодействияэтих молекул. При столкновении одинаковых молекул d1 = d2 = d, R = d и
За время между двумя последовательными столкновениями молекула пролетает некоторый путь l. Разумеется, для каждой отдельной молекулы дело чистой случайности, сколь далеко ей удастся продвинуться без столкновений. Но усредняя путь l по всем молекулам системы, получим физическую величину
называемую средней длиной свободного пробегамолекул. Статистический смысл этой величины таков: отношение малого отрезка длиной dx к дает вероятность столкновения
на пути dx. Пусть Р(х) — вероятность пролететь без столкновений расстояние х. Тогда
—вероятность, пролететь без столкновений расстояние х + dx. Последнее событие складывается из двух независимых событий:
частица пролетела без столкновений расстояние х (вероятность чего равна Р(х));
частица также без столкновений преодолела еще и маленький отрезок пути dx (вероятность чего равна 1 – dx/). По теореме об умножении вероятностей имеем тогда
откуда следует уравнение для вероятности Р(х)
Поскольку вероятность преодолеть нулевое расстояние без столкновений равна единице, имеем дополнительно начальное условие Р(0) = 1. Интегрируя дифференциальное уравнение, находим окончательно
Как видно, чем больше путь х, тем меньше вероятность преодолеть его без столкновений.
Убедимся теперь, что — действительно средняя длина свободного пробега. Вычислим, с какой вероятностью молекула будет иметь длину свободного пробега l. Это значит, что частица пролетела без столкновений расстояние х = l (вероятность чего есть Р(l))и столкнулась с другой частицей непосредственно за этим — на малом отрезке длиной dl (вероятность чего можно найти как dl/). Вероятность dw такого события по теореме умножения вероятностей равна
Находим тогда среднюю длину свободного пробега
(4.2) |
He следует думать, конечно, что вероятность преодолеть расстояние l без столкновений равна нулю: часть молекул может пролететь очень большие расстояния, но лишь крайне небольшая их часть. При х = , как следует из (4.1), вероятность пролета без столкновений равна
то есть 63,2 % частиц испытают столкновения на этом пути. При длине пути х = 2получаем
то есть столкновения суждены уже 86,5 % частиц, при х = 3
в столкновениях участвует уже 95 % частиц, поскольку
Чтобы определить среднее число столкновений n одной молекулы с другими в единицу времени, сделаем следующие допущения:
все молекулы одинаковы, то есть мы не рассматриваем смеси газов;
все молекулы, за исключением той, за которой мы наблюдаем, неподвижны (в дальнейшем мы покажем, как избавиться от этого заведомо неверного предположения);
при столкновениях скорость vОT молекулы не меняется (это предположение, в сущности, того же уровня, что и предыдущее: при упругом столкновении с препятствием, которое остается неподвижным, модуль скорости действительно не меняется (смысл подстрочного индекса «от» станет ясным в дальнейшем)).
Путь нашей молекулы диаметром d остается прямолинейным до тех пор, пока ей не встретится неподвижная молекула, чей центр окажется от линии движения на расстоянии, меньшем R = d. После этого молекула сменит направление движения и будет двигаться прямолинейно до нового соударения. За интервал времени ∆t молекула пройдет ломаный путь vOT ∆t и столкнется со всеми молекулами, попавшими в ломаный цилиндр радиусом d и площадью основания = pd 2 (см. рис. 4.1). Объем этого цилиндра равен pd 2 vOT ∆t. Если n-концентрация молекул в системе (их число в единице объема), то легко найти количество неподвижных молекул в цилиндре, то есть число столкновений DN:
Отсюда следует частота столкновений (то есть число столкновений в единицу времени)
(4.3) |
Избавимся теперь от последствий нашего предположения о неподвижности молекул. Пусть мы следим за молекулой 1, которая движется со скоростью v1, и она сталкивается с молекулой 2, имеющей скорость v2. В системе отсчета, связанной со второй молекулой, она неподвижна, зато первая молекула имеет скорость
Ясно теперь, что именно среднее значение относительной скорости молекул играет роль скорости vОТ, использованной нами при выводе соотношения (4.3) для частоты столкновений. Имеем тогда
(4.4) |
где ????12 — угол между направлениями движения молекул. Из-за хаотичности движения этот угол равновероятно принимает любые значения, так что среднее значение его косинуса равно нулю. А усреднение квадратов скоростей приводит к появлению среднеквадратичной скорости молекул
знакомой нам по предыдущей главе. Получаем в итоге, что
и формула (4.3) записывается в окончательном виде
(4.5) |
Заметим, что, перейдя от скорости молекулы к ее среднеквадратичной скорости, мы на самом деле избавились и от третьего допущения, поскольку vKB постоянна при заданной температуре.
Зная частоту столкновений, можно найти среднюю длину свободного пробега. Действительно, среднее время между двумя последовательными соударениями = 1/n, и за это время частица в среднем проходит путь = vKBt. Таким образом, средняя длина свободного пробега молекулы газа равна
(4.6) |
Поскольку при постоянной температуре концентрация частиц пропорциональна давлению, то с ростом давления длина свободного пробега уменьшается. Это и понятно, так как уменьшается среднее расстояние между частицами. На самом деле молекула не является твердым шариком. Поэтому ее эффективный диаметр d-величина не совсем постоянная: он уменьшается при увеличении температуры, хотя и незначительно. Поэтому средняя длина свободного пробега слегка растет с повышением температуры.
Следует отметить, что среднее расстояние между частицами далеко не совпадает со средней длиной свободного пробега. Ранее мы оценили эффективный диаметр молекулы водяного пара d = 3·10–10 м и среднее расстояние между молекулами при нормальных условиях L = 3·10–9 м. Отсюда находим концентрацию молекул
Подставляя найденное n в выражение для длины свободного пробега, находим
Мы видим, что длина свободного пробега в 200 раз больше диаметра молекулы и в 20 раз больше среднего расстояния между молекулами. Для полноты картины оценим также частоту столкновений. Кинетическая энергия поступательного движения молекулы
Зная массу молекулы воды
получаем оценку среднеквадратичной скорости
Наконец, определяем
Иначе говоря, молекула испытывает 10 млрд соударений в секунду! Линейный размер сосуда, содержащего один литр газа, равен l = 10 см = 0,1 м. При скорости 630 м/с молекула могла бы пролететь путь от стенки до стенки за время
но за это время она испытает
столкновений с другими молекулами.
У нас осталось без обсуждения первое допущение об одинаковости всех молекул. Оно было нужно не по принципиальным соображениям, а для упрощения вывода и окончательных выражений. Если это не так, если мы рассматриваем смесь газов, то компоненты имеют разные концентрации частиц, различные среднеквадратичные скорости, а их молекулы — разные массы. Как следствие, изменится формула для средней длины свободного пробега, причем результаты будут отличаться для молекул различных сортов.
Пример. Найдем, как изменится формула (4.6) для средней длины свободного пробега молекул, если они представляют собой плоские диски, двигающиеся в материале тонкой пленки, будучи не в состоянии из нее вылететь?
Как и прежде, для столкновения молекул диаметрами d1 и d2они должны сблизиться на расстояние
Поэтому при движении молекулы по плоскости пленки она заденет все другие молекулы, которые попадут в ломаный прямоугольник (в отличие от цилиндра в трехмерном случае) шириной 2R и длиной vOT ∆t. Площадь этого прямоугольника
При поверхностной концентрации n молекул (в этом случае n — их число на единицу площади) произойдет ∆N = Sn столкновений. Отсюда для частоты столкновений находим
где мы учли, что, как и прежде, относительная скорость
Отсюда длина свободного пробега для движущихся в плоскости плоских молекул получается равной
При одинаковых молекулах (d1 = d2 = d)
Свидание в лесу, ежик в тумане и атомная бомба. Идея длины свободного пробега может быть использована для оценки видимости в лесу, в тумане или даже для грубой оценки критической массы урана в атомной бомбе.
Представьте себе, что у вас назначено свидание в лесу. С какого максимального расстояния R вы заметите своего партнера (а партнер — вас)? Положим, вы включаете фонарик, чтобы подать ему/ей сигнал. Если не учитывать рассеяние света, то все деревья отбрасывают тени, линейный размер которых можно считать примерно равным диаметру d деревьев. На рис. 4.3 ваше место нахождения отмечено красным кружком, вокруг проведена окружность радиусом R, деревья показаны зелеными кружками, а их тени на окружности отмечены оранжевыми дугами.

Рис. 4.3. Оценка максимального расстояния Rвидимости в лесу
Определим, какую часть окружности покрывают тени. Пусть n плотность посадки деревьев (их число на единицу площади). Если l — среднее расстояние между деревьями, то
Внутрь окружности попадает pR2n деревьев. Полная длина тени на окружности равна поэтому pR2nd. Мы видим, что полная длина тени растет как квадрат радиуса и при каком-то значении R превысит длину окружности 2pR. Но если вся окружность покрыта тенями, то свет дальше не пройдет. Это значение R и будет максимальным расстоянием видимости в лесу. Теперь понятно, что оно определяется из равенства
то есть мы получили оценку
Для численного примера можно взять значения, исходя из своего жизненного опыта. Скажем, свидание назначено среди березок со средним диаметром ствола d = 0,25 м и средним расстоянием между деревьями l = 10 м. Тогда находим R = 800 м.
Установим теперь связь полученного результата с формулой для средней длины свободного пробега. У нас одна молекула (световой луч) не имеет размера (d1 = 0), размер прочих молекул равен среднему диаметру ствола (d2 = d) и, наконец, молекулы (стволы) — покоятся, то есть надо отбросить множитель . Получаем в результате — применительно к нашей задаче — выражение
Таким образом, найденный нами радиус видимости
Вероятность свету преодолеть это расстояние без «столкновений» с деревьями равна
Иными словами, с вероятностью 86.5 % свет будет задержан деревьями.
Свидание в лесу происходило на плоскости. Сейчас мы вернемся в объемный мир. Тот же рисунок изображает теперь сферу радиусом R и препятствия в виде шариков диаметром d. Например, мы хотим оценить видимость для ежика, заблудившегося в тумане, и роль деревьев теперь исполняют водяные капли. Если концентрация капель равна п (их число в единице объема), то внутри сферы находится
Их тени на сфере представляют собой окружности площадью pd2/4. При максимальном расстоянии видимости тени покрывают всю сферу:
Отсюда находим расстояние видимости в тумане
Снова сравним этот результат с формулой (4.6) для длины свободного пробега молекулы в газовой среде, где надо отбросить фактор и взять
Получаем
Вероятность преодолеть путь R = 3l без столкновений равна
Стало быть, с вероятностью 95 % столкновение на этом пути произойдет.
Получим численную оценку. Наши рассуждения годятся, если размер капель заметно (скажем, на один-два порядка) превышает длину световой волны. Так как видимый диапазон имеет длины волн 0,40–0,76 мкм, то для диаметра капель примем оценку d = 10–4 м. Для концентрации капель возьмем значение n = 3·107 м–3(о происхождении этого числа см. чуть ниже). Тогда видимость в тумане будет
Концентрацию капель мы оценили следующим образом. Давление насыщенного водяного пара при, скажем, 20 °С (Т = 293 К) равно рН = 2,3·103 Па. Применяя уравнение Клапейрона — Менделеева, находим плотность водяного пара при 100 % влажности:
При резком понижении температуры весь пар конденсируется в капли указанного размера — образуется густой туман. Масса одной капли равна
Количество образовавшихся капель в объеме V находим как отношение массы пара m к массе капли mКАП. Тогда концентрация капель определится из соотношения
При d = 10–4 м получаем использованное выше значение n = 3·10–7 м–3.
Зависимость расстояния видимости в тумане от размера капель дается, таким образом, соотношением
При предельно малых капельках с диаметром порядка десяти длин световой волны d = 10–5 м видимость сокращается до одного метра. Что называется, «не видно дальше своего носа». При еще меньших размерах капель наша модель становится неверной, так как свет уже нельзя рассматривать просто как совокупность частиц с ничтожно малым размером. Начинают играть роль эффекты дифракции, и выражение для эффективного сечения взаимодействия света с каплями уже не будет определяться чисто геометрическим сечением капель.
Решенная задача имеет также отношение к вопросу о критической массе урана-235, применяемого для изготовления атомных бомб. Вместо света в этой задаче мы имеем нейтроны, а вместо капель — ядра 235U. При столкновении с ядрами нейтроны расщепляют их на осколки, и при этом вылетает еще 3–4 нейтрона. При критическом радиусе Rкрит количество нейтронов не будет уменьшаться и возникнет самоподдерживающаяся цепная реакция — произойдет атомный взрыв. За основу определения критического радиуса можно взять радиус видимости
уменьшенный в kраз (k = 3,5 — коэффициент размножения нейтронов). Поскольку
получаем
Радиус ядра
где r0 = 1,4·10-15 м — радиус ядра с массовым числом А = 1, то есть протона (нейтрона). Поэтому эффективный диаметр взаимодействия равен
В справочнике (например, Российском энциклопедическом словаре) находим плотность урана rU = 19·103 кг/м3. Массу ядра урана-235 определяем по массе протона
Отсюда находим концентрацию ядер
Теперь мы можем оценить критический радиус Rкрит
критический объем Vкрит
и критическую массу Мкрит
Отметим, что никаких секретов производства ядерного оружия мы не выдаем: слишком грубы эти оценки. Единственная наша цель — продемонстрировать еще раз единство законов физики, действующих в самых разнообразных системах.
Источник
