Сжиженные газы в сообщающихся сосудах

26.10.2020
0
Главная › Сосуды › Сжиженные газы в сообщающихся сосудах
Сжиженные газы в сообщающихся сосудах thumbnail

Äàëåå: 1.2. 
Çàäà÷è äëÿ ñàìîñòîÿòåëüíîãî
Ââåðõ: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è
Íàçàä: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è

1.1.  Ïðèìåðû ðåøåíèÿ
çàäà÷

Ïðèìåð 1.1.  Ñæèæåííûå ãàçû õðàíÿò â ñîñóäàõ,
ñîîáùàþùèõñÿ ñ àòìîñôåðîé. Ìîæíî ëè
äîïóñòèòü èñïàðåíèå æèäêîãî àçîòà îáúåìîì $0,5,{ë}$ è
ïëîòíîñòüþ
$0,81,{ã/ñì}^3$â
çàêðûòîì ñîñóäå îáúåìîì $10,{ë}$ ïðè íàãðåâàíèè
åãî äî òåìïåðàòóðû $20^circ C$, åñëè ñòåíêè ñîñóäà
âûäåðæèâàþò äàâëåíèå
$20,{àòì}$?

hbox to 0.4hsizeÐåøåíèå.
Ïðè ïîâûøåíèè òåìïåðàòóðû æèäêèé àçîò ïåðåéäåò â ãàçîîáðàçíîå
ñîñòîÿíèå.
Ïðèìåì åãî ïðè òåìïåðàòóðå $20^circ C$ çà èäåàëüíûé ãàç è
ïðèìåíèì äëÿ ðåøåíèÿ
óðàâíåíèå Êëàïåéðîíà – Ìåíäåëååâà:

begin{displaymath} PV = {movermu}RT,, end{displaymath}(1)


ãäå $P$, $V$ è $T$ – äàâëåíèå, îáúåì è
òåìïåðàòóðà ãàçà; $m$ – åãî ìàññà, $mu$ – ìàññà
ìîëÿ àçîòà, ðàâíàÿ $28cdot 10^{-3},{êã/ìîëü}$; $R$ – óíèâåðñàëüíàÿ
ãàçîâàÿ ïîñòîÿííàÿ.

Äëÿ îòâåòà íà âîïðîñ çàäà÷è íóæíî îïðåäåëèòü äàâëåíèå ãàçîîáðàçíîãî
àçîòà è ñðàâíèòü åãî ñ
ìàêñèìàëüíî äîïóñòèìûì.

Âûðàçèì èñêîìîå äàâëåíèå èç óðàâíåíèÿ 1:

begin{displaymath} P_x = {mRTovermu V},, end{displaymath}(2)


çäåñü íåèçâåñòíà ìàññà ãàçà, åå ìîæíî îïðåäåëèòü ÷åðåç îáúåì è
ïëîòíîñòü æèäêîãî àçîòà:
$m= rho_1V_1$. Âûðàæåíèå äëÿ èñêîìîãî äàâëåíèÿ â îáùåì âèäå:

begin{displaymath} P_x = {rho_1V_1RTovermu V},. end{displaymath}(3)


Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû èñêîìîé âåëè÷èíû:

begin{displaymath}[P_x]={{êã}cdot{ì}^3cdot{Äæ}cdot{Ê}cdot{ìîëü}over {ì}^3 ... ...{{Äæ}over{ì}^3}= {{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà.}end{displaymath}

Ýòî åäèíèöà äàâëåíèÿ â ÑÈ, ñëåäîâàòåëüíî, âûðàæåíèå â îáùåì âèäå
ïîëó÷åíî ïðàâèëüíî.

Âû÷èñëåíèÿ: ïîäñòàâèì ÷èñëà (âñå îíè äîëæíû áûòü âûðàæåíû â
ÑÈ):

begin{displaymath}P_x={8,1cdot 10^2cdot 5cdot 10^{-4}cdot 8,3 cdot 293over 28cdot 10^{-3}cdot 10^{-2}},{Ïà},.end{displaymath}

Ïðåæäå ÷åì âû÷èñëÿòü, ïðîâåäåì äåéñòâèÿ ñî ñòåïåíÿìè:

begin{displaymath}P_x={8,1cdot 5cdot 8,3 cdot 293over 28}cdot 10^{3},{Ïà}=3,52cdot 10^{6},{Ïà},.end{displaymath}

Èñêîìîå äàâëåíèå ðàâíî $3,52cdot 10^6,{Ïà}$ èëè $35,2 {àòì}$ è ïðåâûøàåò
äîïóñòèìîå.

Îòâåò: èñïàðåíèå æèäêîãî àçîòà äàííîé ìàññû â çàêðûòîì ñîñóäå
óêàçàííîãî îáúåìà íåëüçÿ
äîïóñòèòü, òàê êàê ïðè $20^circ C$ äàâëåíèå ïðåâûñèò
äîïóñòèìîå. Ïîýòîìó ñæèæåííûå ãàçû õðàíÿò
â îòêðûòûõ ñîñóäàõ.

Ïðèìåð 1.2. Öèëèíäðè÷åñêàÿ òðóáêà äëèíîé $ell$ íàïîëîâèíó ïîãðóæåíà â ðòóòü. Çàêðûâ åå ñâåðõó,
òðóáêó âûíèìàþò, ïðè ýòîì ÷àñòü ðòóòè âûëèâàåòñÿ. Êàêîé äëèíû ñòîëáèê
ðòóòè îñòàíåòñÿ â òðóáêå,
åñëè àòìîñôåðíîå äàâëåíèå ðàâíî $H$ ìì ðò. ñò.?

hbox to 0.4hsizeÐåøåíèå.
Ïðèìåì âîçäóõ, íàõîäÿùèéñÿ â òðóáêå íàä ðòóòüþ, çà èäåàëüíûé ãàç.
Ïîñêîëüêó â óñëîâèè çàäà÷è
èçìåíåíèå òåìïåðàòóðû íå îãîâîðåíî, ê ñòîëáèêó âîçäóõà ìîæíî ïðèìåíèòü
çàêîí Áîéëÿ – Ìàðèîòòà:

begin{displaymath} P_1V_1 = P_2V_2,, end{displaymath}(4)


ãäå $P_1$ è $V_1$ — äàâëåíèå è îáúåì
âîçäóõà â ïåðâîì ñîñòîÿíèè; $P_2$ è $V_2$ — òî æå âî
âòîðîì ñîñòîÿíèè.

begin{center}vbox{defbasepath{D:/html/work/link1/metod} defmetdir{met8} getpic{M21}}end{center}

Äëÿ îòâåòà íà âîïðîñ çàäà÷è íóæíî âûðàçèòü ïàðàìåòðû ãàçà ÷åðåç
èçâåñòíûå â îáùåì âèäå
âåëè÷èíû – $H$ è $ell$. Îáîçíà÷èì èñêîìóþ
äëèíó ñòîëáèêà ðòóòè ÷åðåç $X$.  ïåðâîì
ñîñòîÿíèè ñòîëáèê âîçäóõà äëèíîé $ell/2$, òî åñòü îáúåìîì
$V_1={Sellover 2}$ ($S$ – ïëîùàäü
ñå÷åíèÿ òðóáêè), íàõîäèëñÿ ïîä àòìîñôåðíûì äàâëåíèåì, òàê êàê òðóáêà
áûëà îòêðûòà ñâåðõó.
Âûðàçèì àòìîñôåðíîå äàâëåíèå: $P_1 = rho gH$,
ãäå $rho$ – ïëîòíîñòü ðòóòè. Òàêèì îáðàçîì,

begin{displaymath} P_1V_1 = rho gH{Sellover 2},. end{displaymath}(5)


Âî âòîðîì ñîñòîÿíèè äëèíà ñòîëáèêà âîçäóõà ñòàëà ðàâíîé $(ell-X)$, à åãî îáúåì $V_2=S(ell-X)$.
Äàâëåíèå âîçäóõà â ñóììå ñ äàâëåíèåì îñòàâøåãîñÿ ñòîëáèêà ðòóòè âûñîòîé
$X$ óðàâíîâåøèâàåòñÿ
àòìîñôåðíûì äàâëåíèåì, äåéñòâóþùèì ñîãëàñíî çàêîíó Ïàñêàëÿ íà íèæíèé
îòêðûòûé êîíåö òðóáêè:
$P_2+rho gX=rho gH$, îòêóäà äàâëåíèå

begin{displaymath}P_2=rho g(H-X) {è}end{displaymath}

begin{displaymath} P_2V_2 = rho g(H-X)S(ell-X),. end{displaymath}(6)


Ïîäñòàâèâ âûðàæåíèÿ (5 è 6)
â èñõîäíîå óðàâíåíèå (4) è
ñîêðàòèâ íà $g, S, rho$, ïîëó÷èì êâàäðàòíîå óðàâíåíèå
îòíîñèòåëüíî $X$:

begin{displaymath} X^2 - (H+ell)X+{ell Hover 2}=0,. end{displaymath}(7)


Äâà êîðíÿ ýòîãî óðàâíåíèÿ:

begin{displaymath}X_{1,2} = {(H+ell)pm sqrt{(H+ell)^2-2ell H}over 2}={(H+ell)pm sqrt{H^2+ell^2}over 2},.end{displaymath}

Ìàòåìàòè÷åñêàÿ ÷àñòü çàäà÷è âûïîëíåíà: íàéäåíû êîðíè êâàäðàòíîãî
óðàâíåíèÿ. Îäíàêî
óñëîâèþ ôèçè÷åñêîé çàäà÷è êîðåíü óðàâíåíèÿ ñî çíàêîì “+” íå
óäîâëåòâîðÿåò, òàê êàê äëèíà
ñòîëáèêà ðòóòè â ýòîì ñëó÷àå ïðåâûøàåò äëèíó òðóáêè $ell$. Ïîýòîìó

$X={(H+ell)-sqrt{H^2+ell^2}over 2}$. Âèäíî, ÷òî $X$ ïîëó÷èòñÿ â åäèíèöàõ äëèíû.
 ÷èñëîâîì âàðèàíòå ðåøåíèÿ ïîäîáíîé çàäà÷è $H$ è $ell$ íóæíî ïîäñòàâëÿòü â îäèíàêîâûõ
åäèíèöàõ äëèíû, íàïðèìåð, â ì.

Îòâåò: èñêîìàÿ äëèíà ñòîëáèêà âûðàæàåòñÿ òàê:

begin{displaymath}X={(H+ell)-sqrt{H^2+ell^2}over 2},.end{displaymath}


Ïðèìåð 1.3. Â ñòåêëÿííîì ñôåðè÷åñêîì ñîñóäå ñ
âíóòðåííèì äèàìåòðîì $3,{ñì}$ íàõîäèòñÿ àçîò,
äàâëåíèå êîòîðîãî ïðè òåìïåðàòóðå $-190^circ C$
ðàâíî 1,33 Ïà. Íà ñòåíêàõ âíóòðè ñîñóäà èìååòñÿ
ìîíîìîëåêóëÿðíûé (òîëùèíîé â îäíó ìîëåêóëó) ñëîé àäñîðáèðîâàííîãî, òî
åñòü ïîãëîùåííîãî
ïîâåðõíîñòíûì ñëîåì, àçîòà. Îäíà ìîëåêóëà çàíèìàåò ïëîùàäü
$10^{-15},{ñì}^2$. Íàéòè
äàâëåíèå àçîòà â ñîñóäå ïðè òåìïåðàòóðå $427^circ C$,
ïðè êîòîðîé îí ïîëíîñòüþ äåñîðáèðóåòñÿ
ñî ñòåíîê.

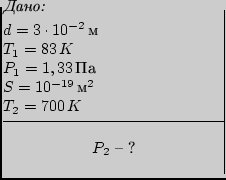hbox to 0.4hsizeÐåøåíèå.
Àçîò ïðè òàêîì íèçêîì äàâëåíèè ìîæíî ðàññìàòðèâàòü êàê èäåàëüíûé ãàç è
ïðèìåíèòü ñîîòâåòñòâóþùóþ òåîðèþ.
Èñêîìîå äàâëåíèå $P_2$ áóäåò ñêëàäûâàòüñÿ èç äàâëåíèÿ
ãàçà, ïåðâîíà÷àëüíî íàõîäèâøåãîñÿ
â ñîñóäå $P_2'$, è äàâëåíèÿ $P_2''$, êîòîðîå ñîçäàäóò
ìîëåêóëû, ïåðåøåäøèå ñî ñòåíîê
â cocóä ïðè òåìïåðàòóðå $T_2$:

begin{displaymath} P_2 = P_2'+P_2'',. end{displaymath}(8)


Âûðàçèì äàâëåíèå $P_2'$, ó÷èòûâàÿ, ÷òî ïîâûøåíèå
òåìïåðàòóðû ïðîèñõîäèò ïðè ïîñòîÿííîì
îáúåìå. Ñîãëàñíî çàêîíó Øàðëÿ:

begin{displaymath}{P_1over T_1}={P_2'over T_2},,end{displaymath}


begin{displaymath} {îòêóäàquadquad} P_2' = P_1{T_2over T_1},. end{displaymath}(9)


Âèäíî, ÷òî åäèíèöà èçìåðåíèÿ $P_2'$ ïîëó÷àåòñÿ òàêàÿ æå,
êàê $P_1$ – Ïà.

Äàâëåíèå $P_2''$ âûðàçèì èç îñíîâíîãî óðàâíåíèÿ
êèíåòè÷åñêîé òåîðèè èäåàëüíîãî ãàçà:

Читайте также:  Препараты для чистки сосудов от тромбов

begin{displaymath} P_2'' = nkT_2={Nover V}kT_2,, end{displaymath}(10)


ãäå $N$ – îáùåå ÷èñëî äåñîðáèðîâàííûõ ìîëåêóë, $n$ – èõ êîíöåíòðàöèÿ,
$k$ – ïîñòîÿííàÿ Áîëüöìàíà, $V$ – îáúåì ñîñóäà:
$V={pi d^3over 6}$.
Îáùåå ÷èñëî ìîëåêóë, ïåðåøåäøèõ ñî ñòåíîê â ñîñóä, ìîæíî âûðàçèòü êàê
îòíîøåíèå
ïëîùàäè âíóòðåííåé ïîâåðõíîñòè ñôåðè÷åñêîãî ñîñóäà $pi d^2$
ê ïëîùàäè îäíîé ìîëåêóëû: $N={pi d^2over S}$. Îêîí÷àòåëüíî äëÿ äàâëåíèÿ $P_2''$ ïîëó÷èì:

begin{displaymath} P_2'' = {pi d^2cdot 6cdot kT_2over Spi d^3}={6kT_2over Sd},. end{displaymath}(11)


Ïðîâåðêà åäèíèö èçìåðåíèÿ èñêîìîé âåëè÷èíû:

begin{displaymath}[P_2'']={{Äæ}cdot{Ê}over{Ê}cdot{ì}^2cdot{ì}}= {{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà},.end{displaymath}

Ïîëó÷åíà åäèíèöà äàâëåíèÿ, òî åñòü âûðàæåíèå â îáùåì âèäå ïðàâèëüíî.

Òàêèì îáðàçîì,

begin{displaymath} P_2 = P_1 {T_2over T_1}+{6kT_2over Sd},. end{displaymath}(12)


Âû÷èñëåíèÿ:

begin{displaymath}P_2=left ({1,3cdot 7cdot 10^2over 83}+{6cdot 1,38cdot 1... ...7cdot 10^{2}over 10^{-19}cdot 3cdot 10^{-2}}right ),{Ïà}=end{displaymath}

begin{displaymath}=left ( 11,22+{6cdot 1,38 cdot 7over 3}right),{Ïà}=(11,22+19,32),{Ïà}=30,54,{Ïà},.end{displaymath}

Âèäíî, ÷òî ïî ïîðÿäêó âåëè÷èíû äåéñòâèå îáîèõ ôàêòîðîâ: ðîñòà äàâëåíèÿ
ñ ïîâûøåíèåì
òåìïåðàòóðû è óâåëè÷åíèÿ êîíöåíòðàöèè ìîëåêóë â ñîñóäå — ñîãëàñóåòñÿ
ïî ïîðÿäêó âåëè÷èí.
Âòîðîé ôàêòîð â äàííîì ñëó÷àå îêàçûâàåò áîëüøåå äåéñòâèå.

Îòâåò: äàâëåíèå àçîòà â ñîñóäå ñòàíåò ðàâíûì 30,54 Ïà.

Ïðèìåð 1.4. Íàéòè ñðåäíåå ÷èñëî âñåõ ïàðíûõ
ñòîëêíîâåíèé â ñåêóíäó ìîëåêóë êèñëîðîäà,
íàõîäÿùèõñÿ â îáúåìå $1,{ñì}^3$ ïðè òåìïåðàòóðå $17^circ C$ è äàâëåíèè 666,5
Ïà.

hbox to 0.4hsizeÐåøåíèå.
Ñîãëàñíî ÌÊÒ èäåàëüíîãî ãàçà ñðåäíåå ÷èñëî ñòîëêíîâåíèé â ñåêóíäó

îäíîé
ìîëåêóëû

ðàâíî:

begin{displaymath} overline{Z} = sqrt{2}pi d^2noverline{v},, end{displaymath}(13)


ãäå $d$ – ýôôåêòèâíûé äèàìåòð ìîëåêóëû, $n$ – êîíöåíòðàöèÿ ãàçà, $overline{v}$
–
ñðåäíÿÿ àðèôìåòè÷åñêàÿ ñêîðîñòü ìîëåêóë.

Åñëè ó÷èòûâàòü òîëüêî ïàðíûå

ñòîëêíîâåíèÿ, ÷èñëî âñåõ ñòîëêíîâåíèé â
ñåêóíäó áóäåò áîëüøå â ${Nover 2}={nVover 2}$ ðàç, ãäå $N$ – îáùåå
÷èñëî ìîëåêóë.

Òîãäà èñêîìîå ÷èñëî ñòîëêíîâåíèé âûðàçèòñÿ òàê:

begin{displaymath} overline{Z}={sqrt{2}pi d^2overline{v}n^2Vover 2},. end{displaymath}(14)


Äàëåå ñëåäóåò âûðàçèòü êîíöåíòðàöèþ ãàçà èç îñíîâíîãî óðàâíåíèÿ
êèíåòè÷åñêîé òåîðèè
èäåàëüíîãî ãàçà: $p=nkT$, à ñðåäíþþ àðèôìåòè÷åñêóþ ñêîðîñòü
— ÷åðåç ïàðàìåòðû ãàçà:
$overline{v}=sqrt{8RToverpimu}$, ãäå $R$ — óíèâåðñàëüíàÿ (ìîëÿðíàÿ) ãàçîâàÿ ïîñòîÿííàÿ.
Ïîñëå ïîäñòàíîâêè äëÿ èñêîìîé âåëè÷èíû ïîëó÷àåòñÿ:

begin{displaymath} overline{Z}=2left({dPover kT}right)^2Vsqrt{pi RTovermu},. end{displaymath}(15)


 ýòîì âûðàæåíèè âñå, êðîìå äèàìåòðà ìîëåêóëû, èçâåñòíî. Ýòî ÷èñëî
âçÿòî èç òàáëèöû.

Ïðîâåðêà åäèíèöû èçìåðåíèÿ èñêîìîé âåëè÷èíû:

begin{displaymath}[overline{Z}]={{ì}^2cdot{Í}^2cdot{Ê}^2cdot{ì}^3cdot{Äæ}^... ... 2}over{ñ}cdot{ì}^{3over 2}cdot{êã}^{1over 2}}={ñ}^{-1},.end{displaymath}

Íàèìåíîâàíèå $c^{-1}$ ñîîòâåòñòâóåò ÷èñëó ñòîëêíîâåíèé â
ñåêóíäó.

Âû÷èñëåíèÿ:

begin{displaymath}overline{Z}={2cdot 12,25cdot 10^{-20}cdot (666,5)^2cdot ... ...over327cdot 10^{-3}},{ñ}^{-1} =3,3cdot 10^{24},{ñ}^{-1},.end{displaymath}

Îòâåò: ïðè óêàçàííûõ óñëîâèÿõ ïðîèñõîäèò
$3,3cdot 10^{24}$ ïàðíûõ ñòîëêíîâåíèé ìîëåêóë
â ñåêóíäó. Ýòî ÷èñëî çàâèñèò îò ïàðàìåòðîâ ñîñòîÿíèÿ ($P, T$), îáúåìà ãàçà è åãî
èíäèâèäóàëüíûõ õàðàêòåðèñòèê: äèàìåòðà ìîëåêóëû è ìîëÿðíîé ìàññû.

Ïðèìåð 1.5. Ðàññòîÿíèå ìåæäó ñòåíêàìè ñîñóäà ðàâíî $8,{ìì}$. Ïðè êàêîì äàâëåíèè âÿçêîñòü
ãàçà, íàõîäÿùåãîñÿ ìåæäó íèìè, íà÷íåò óìåíüøàòüñÿ ïðè îòêà÷êå?
Òåìïåðàòóðà ãàçà ðàâíà
$17^circ C$. Äèàìåòð ìîëåêóëû ñîñòàâëÿåò
$3cdot 10^{-10},{ì}$.

hbox to 0.4hsizeÐåøåíèå.
Òåîðåòè÷åñêè âÿçêîñòü ãàçà ïðè íå ñëèøêîì íèçêèõ äàâëåíèÿõ 
íå çàâèñèò îò íåãî:

begin{displaymath} eta = {1over 3}overline{v}overline{lambda}rho,, end{displaymath}(16)


òàê êàê $overline{lambda}$ – ñðåäíÿÿ äëèíà ñâîáîäíîãî ïðîáåãà ìîëåêóë îáðàòíî
ïðîïîðöèîíàëüíà äàâëåíèþ ïðè ïîñòîÿííîé òåìïåðàòóðå:

begin{displaymath} overline{lambda} = {1over sqrt{2}pi d^2n}={kTover sqrt{2}pi d^2P},, end{displaymath}(17)


à ïëîòíîñòü ãàçà $rho$ ïðÿìî ïðîïîðöèîíàëüíà äàâëåíèþ.
Âûðàæåíèå äëÿ ïëîòíîñòè èäåàëüíîãî ãàçà
ìîæíî ïîëó÷èòü èç óðàâíåíèÿ Êëàïåéðîíà – Ìåíäåëååâà:
$PV = {movermu}RT$, ó÷èòûâàÿ,
÷òî ïëîòíîñòü — ýòî ìàññà åäèíèöû îáúåìà:
$rho = {mover V}$. Ïîëó÷àåòñÿ, ÷òî
$rho = {mu Pover RT}$.

Ïðè íèçêîì äàâëåíèè ñðåäíÿÿ äëèíà ñâîáîäíîãî ïðîáåãà
ïåðåñòàåò
çàâèñåòü îò äàâëåíèÿ è îïðåäåëÿåòñÿ ðàçìåðàìè ñîñóäà:

begin{displaymath} overline{lambda} = ell,. end{displaymath}(18)


Ìîëåêóëû äâèæóòñÿ îò ñòåíêè ê ñòåíêå, íå ñòàëêèâàÿñü ìåæäó ñîáîé.
Âÿçêîñòü ãàçà íà÷íåò
óìåíüøàòüñÿ ïðè äàëüíåéøåé îòêà÷êå ñîñóäà çà ñ÷åò óìåíüøåíèÿ
êîíöåíòðàöèè ìîëåêóë
(ïëîòíîñòè ãàçà).

Äëÿ ðåøåíèÿ çàäà÷è íóæíî ïðèðàâíÿòü âûðàæåíèå äëÿ ñðåäíåé äëèíû
ñâîáîäíîãî
ïðîáeãa ìîëåêóë $overline{lambda}$ ðàññòîÿíèþ ìåæäó ñòåíêàìè ñîñóäà:

begin{displaymath}ell = {kTover sqrt{2}pi d^2P},end{displaymath}



è âûðàçèòü äàâëåíèå. Ïîëó÷àåì:

begin{displaymath} P = {kTover sqrt{2}pi d^2ell},. end{displaymath}(19)


 ýòîì âûðàæåíèè äëÿ äàâëåíèÿ âñå èçâåñòíî.

Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû èçìåðåíèÿ:

begin{displaymath}[P]={{Äæ}cdot{Ê}over{Ê}cdot{ì}^2cdot{ì}}={{Äæ}over {ì}^3}={{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà},.end{displaymath}

Âûðàæåíèå äëÿ äàâëåíèÿ â îáùåì âèäå ïîëó÷åíî ïðàâèëüíî.

Âû÷èñëåíèÿ:

begin{displaymath}P={1,38cdot 10^{-23}cdot 290over sqrt{2}cdot 3,14cdot 9... ...290over sqrt{2}cdot 3,14cdot 9cdot 8},{Ïà}=1,26, {Ïà},.end{displaymath}

Ïîëó÷åííîå ÷èñëî çíà÷èòåëüíî ìåíüøå âåëè÷èíû àòìîñôåðíîãî äàâëåíèÿ. Äëÿ
äàííîãî ãàçà ïðè íåèçìåííîé
òåìïåðàòóðå îíî îïðåäåëÿåòñÿ òîëüêî ðàçìåðàìè ñîñóäà $ell$.

Îòâåò: ïðè äàâëåíèè 1,26 Ïà âÿçêîñòü ãàçà íà÷íåò óìåíüøàòüñÿ
ïðè îòêà÷êå.
Óêàçàíèå: ïîäîáíûì îáðàçîì ðåøàþòñÿ çàäà÷è, ñâÿçàííûå ñ
êîýôôèöèåíòîì òåïëîïðîâîäíîñòè
èäåàëüíîãî ãàçà:

begin{displaymath}chi = {1over 3}overline{v}overline{lambda}rho c_v,,end{displaymath}



ãäå $c_v$ – óäåëüíàÿ òåïëîåìêîñòü
ïðè ïîñòîÿííîì îáúåìå:

begin{displaymath}c_v={iover 2}{Rovermu} (i{ -- ÷èñëî ñòåïåíåé ñâîáîäû ìîëåêóëû}).end{displaymath}


Ïðèìåð 1.6. 10 ë àçîòà, íàõîäÿùåãîñÿ ïîä äàâëåíèåì $10^5,{Ïà}$, ðàñøèðÿþòñÿ âäâîå.
Íàéòè êîíå÷íîå äàâëåíèå è ñîâåðøåííóþ ãàçîì ðàáîòó â ñëó÷àÿõ
èçîáàðè÷åñêîãî,
èçîòåðìè÷åñêîãî è àäèàáàòè÷åñêîãî ïðîöåññîâ. Ìîëåêóëû àçîòà èìåþò ïÿòü
ñòåïåíåé ñâîáîäû.

hbox to 0.4hsizeÐåøåíèå.
Ïðèìåì àçîò â äàííûõ óñëîâèÿõ çà èäåàëüíûé ãàç.
1. Ïðè èçîáàðè÷åñêîì ïðîöåññå äàâëåíèå ãàçà íå ìåíÿåòñÿ, ïîýòîìó $P_2=P_1$.
Ýëåìåíòàðíàÿ ðàáîòà ðàñøèðåíèÿ ðàâíà â îáùåì ñëó÷àå $PdV$, ãäå $P$ – äàâëåíèå,
$dV$ – áåñêîíå÷íî ìàëûé îáúåì. Ïîëíàÿ ðàáîòà íàõîäèòñÿ ïóòåì
èíòåãðèðîâàíèÿ, è âåëè÷èíà
eå çàâèñèò îò âèäà ïðîöåññà.

Ïðè èçîáàðè÷åñêîì ïðîöåññå

begin{displaymath} A_1=intlimits_{V_1}^{V_2}{PdV}=P(V_2-V_1),. end{displaymath}(20)


Ïðîâåðèì åäèíèöó èçìåðåíèÿ ðàáîòû:

begin{displaymath}[A]= {{Í}cdot {ì}^3over {ì}^2}={Í}cdot{ì}={Äæ},.end{displaymath}

2.  èçîòåðìè÷åñêîì ïðîöåññå òåìïåðàòóðà îñòàåòñÿ ïîñòîÿííîé, à
äàâëåíèÿ è îáúåìû â äâóõ
ñîñòîÿíèÿõ èäåàëüíîãî ãàçà ñâÿçàíû çàêîíîì Áîéëÿ – Ìàðèîòòà: $P_1V_1=P_2V_2$, îòêóäà
$P_2'={P_1V_1over V_2}$. Âèäíî, ÷òî çäåñü äëÿ åäèíèöû íåèçâåñòíîãî äàâëåíèÿ
ïîëó÷àåòñÿ
Ïà (ïàñêàëü).

Читайте также:  На коже на лице мелкие красные сосуды

Ðàáîòà èçîòåðìè÷åñêîãî ðàñøèðåíèÿ ðàññ÷èòûâàåòñÿ òàê:

begin{displaymath}A_2=int{PdV}=intlimits_{V_1}^{V_2}{{m over mu}RT{dVover V}}={movermu}RTln{V_2 over V_1},.end{displaymath}



Çäåñü äàâëåíèå âûðàæåíî èç óðàâíåíèÿ Êëàïåéðîíà – Ìåíäåëååâà.
Òåìïåðàòóðà
íåèçâåñòíà, ïîýòîìó, ïðèìåíèâ åùå ðàç óðàâíåíèå Êëàïåéðîíà –
Ìåíäåëååâà, ïîëó÷èì âûðàæåíèå
äëÿ èñêîìîé ðàáîòû ÷åðåç èçâåñòíûå â óñëîâèè âåëè÷èíû:

begin{displaymath} A_2 = P_1V_1ln{V_2over V_1},. end{displaymath}(21)


Ðåçóëüòàò íå èçìåíèòñÿ, åñëè ïîäñòàâèòü êîíå÷íûå äàâëåíèå è îáúåì $P_2$ è
$V_2$ èëè âìåñòî îòíîøåíèÿ ${V_2over V_1}$ âçÿòü ${P_1over P_2}$.

3. Êîíå÷íîå äàâëåíèå àäèàáàòè÷åñêîãî ðàñøèðåíèÿ âûðàçèì èç óðàâíåíèÿ
Ïóàññîíà:

begin{displaymath}P_2''=P_1left({V_1over V_2}right)^gamma,, {ãäå }gamma={C_pover C_V}={i+2over i}end{displaymath}



($i$ – ÷èñëî ñòåïåíåé ñâîáîäû ìîëåêóëû).

Ðàáîòà â ýòîì ïðîöåññå ñîâåðøàåòñÿ çà ñ÷åò óáûëè âíóòðåííåé ýíåðãèè
ãàçà:

begin{displaymath}A_3=-Delta u={movermu}C_V(T_1-T_2)={movermu}C_V T_1 left(1-{T_2over T_1}right),,end{displaymath}



ãäå $C_V$ – ìîëÿðíàÿ òåïëîåìêîñòü ïðè ïîñòîÿííîì îáúåìå:

begin{displaymath}C_V={iover 2}R={Rover gamma-1},.end{displaymath}

begin{center}vbox{getpic{M22}}end{center}

 ýòîé çàäà÷å òåìïåðàòóðû íå çàäàíû, ïîýòîìó îòíîøåíèå òåìïåðàòóð
ñëåäóåò çàìåíèòü îòíîøåíèåì
îáúåìîâ
${T_2over T_1}=left({V_1over V_2}right)^{gamma-1}$ è âîñïîëüçîâàòüñÿ
óðàâíåíèåì ñîñòîÿíèÿ èäåàëüíîãî ãàçà:

begin{displaymath}A_3={movermu}{Rover(gamma-1)}T_1left(1-{T_2over T_1}ri... ...amma-1)} left(1-left({V_1over V_2}right)^{gamma-1}right)=end{displaymath}


begin{displaymath} ={1overgamma-1}(P_1V_1-P_2''V_2),. end{displaymath}(22)


Çäåñü âñå èçâåñòíî, êîíå÷íîå äàâëåíèå ìîæíî ðàññ÷èòàòü îòäåëüíî.

Âû÷èñëåíèÿ:

  1. $P_2=P_1=10^{5},{Ïà},;quad A_1=10^{5}cdot 10^{-2},{Äæ}=10^{3},{Äæ}$.
  2. $P_2'={10^{5}cdot 10^{-2}over 2cdot 10^{-2}},{Ïà}=5cdot 10^{4},{Ïà},;$

    $A_2=10^{5}cdot 10^{-2}ln{2cdot 10^{-2}over 10^{-2}},{Äæ}=10^{3}ln{2},{Äæ}= 6,9cdot 10^2,{Äæ}.$

  3. $P_2''= 10^{5}cdot 0,5^{1,4},{Ïà}=3,8cdot 10^4,{Ïà},;$

    $A_3={1over 0,4}(10^3-760),{Äæ}=600,{Äæ},.$

Òàêèì îáðàçîì, íàèáîëüøåå èçìåíåíèå äàâëåíèÿ ïðîèñõîäèò ïðè
àäèàáàòè÷åñêîì ðàñøèðåíèè,
à íàèáîëüøàÿ ðàáîòà ñîâåðøàåòñÿ ïðè èçîáàðè÷åñêîì. Êà÷åñòâåííî
ðåçóëüòàòû ïðåäñòàâëåíû
íà ðèñóíêå. Ïëîùàäè ôèãóð ïîä ãðàôèêàìè ïðîöåññîâ ïîçâîëÿþò ñóäèòü î
ñîîòíîøåíèè ñîâåðøåííîé
ðàáîòû.

Îòâåò:
$10^{5},{Ïà},, 10^{3},{Äæ},; 5cdot 10^{4},{Ïà},, 690,{Äæ},; 3,8cdot 10^4,{Ïà},, 600,{Äæ}.$

Ïðèìåð 1.7. Õîëîäèëüíàÿ ìàøèíà, ðàáîòàþùàÿ ïî
îáðàòíîìó öèêëó Êàðíî, ïåðåäàåò òåïëîòó îò
õîëîäèëüíèêà ñ âîäîé ïðè òåìïåðàòóðå $0^circ C$
êèïÿòèëüíèêó ñ âîäîé ïðè òåìïåðàòóðå $100^circ$C.
Êàêóþ ìàññó âîäû íóæíî çàìîðîçèòü â õîëîäèëüíèêå, ÷òîáû ïðåâðàòèòü â
ïàð 1 êã âîäû â
êèïÿòèëüíèêå? Óäåëüíàÿ òåïëîòà ïàðîîáðàçîâàíèÿ âîäû ïðè $100^circ$Ñ ðàâíà
$2,26cdot 10^6,{Äæ/êã}$. Óäåëüíàÿ òåïëîòà ïëàâëåíèÿ ëüäà ðàâíà
$3,35cdot 10^5,{Äæ/êã}$.

hbox to 0.4hsizeÐåøåíèå.
Õîëîäèëüíàÿ ìàøèíà çà ñ÷åò âíåøíåé ðàáîòû îòíèìàåò íåêîòîðîå êîëè÷åñòâî
òåïëîòû $Q_2$
îò ìåíåå íàãðåòîãî òåëà ïðè òåìïåðàòóðå $T_2$ è
ïåðåäàåò òåïëîòó $Q_1$ áîëåå íàãðåòîìy òåëó
ïðè òåìïåðàòóðå $T_1$.
Êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ åå
$eta={Aover Q_1}={Q_1-Q_2over Q_1}$.

Òàêîå æå ñîîòíîøåíèå ñïðàâåäëèâî è äëÿ òåïëîâîé ìàøèíû, ñîâåðøàþùåé
ðàáîòó çà ñ÷åò ÷àñòè
òåïëîòû, âçÿòîé ó áîëåå íàãðåòîãî òåëà.

Íàèáîëüøèé êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ ñîîòâåòñòâóåò èäåàëüíîìó
(òåîðåòè÷åñêîìó) öèêëó Êàðíî.
 ýòîì ñëó÷àå
$eta={Q_1-Q_2over Q_1}={T_1-T_2over T_1}$, òî åñòü êïä
îïðåäåëÿåòñÿ òîëüêî
òåìïåðàòóðàìè íàãðåâàòåëÿ (òåëà ïðè òåìïåðàòóðå $T_1$) è
õîëîäèëüíèêà ($T_2$). Ñ ïîìîùüþ
ýòîãî ñîîòíîøåíèÿ ðåøàåòñÿ áîëüøèíñòâî çàäà÷, ñâÿçàííûõ ñ ðàáîòîé
òåïëîâûõ è õîëîäèëüíûõ ìàøèí.
 ðåàëüíûõ ìàøèíàõ êïä çíà÷èòåëüíî ìåíüøå, ÷åì
${T_1-T_2over T_1}$.

 äàííîé çàäà÷å êîëè÷åñòâî òåïëîòû $Q_1$, ïåðåäàâàåìîå áîëåå
íàãðåòîìó òåëó, ðàâíî $rm_1$,
à êîëè÷åñòâî òåïëîòû $Q_2$, âçÿòîå îò ìåíåå íàãðåòîãî òåëà,
ðàâíî $lambda m_2$, ïîýòîìó
ñïðàâåäëèâî ðàâåíñòâî:

begin{displaymath} {rm_1-lambda m_2over rm_1}={T_1-T_2over T_1},, end{displaymath}(23)


êîòîðîå ìîæíî ïðåîáðàçîâàòü òàê:

begin{displaymath}{lambda m_2over rm_1}={T_2over T_1},,end{displaymath}


begin{displaymath} {îòêóäà}quad m_2={rm_1T_2overlambda T_1},. end{displaymath}(24)


Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû:

begin{displaymath}[m]= {{Äæ}cdot {êã}cdot {Ê}cdot {êã}over{êã}cdot{Äæ}cdot {Ê}}={êã},.end{displaymath}

Âû÷èñëåíèÿ:

begin{displaymath}m_2={2,26cdot 10^{6}cdot 1cdot 273over 3,35cdot 10^{5}c... ...73},{êã}={2,26cdot 2730over 3,35cdot 373},{êã}=4,94,{êã}.end{displaymath}

Îòâåò: ÷òîáû èñïàðèòü 1 êã âîäû â êèïÿòèëüíèêå ïðè çàäàííûõ
óñëîâèÿõ, íóæíî
çàìîðîçèòü 4,94 êã âîäû â õîëîäèëüíèêå.

Äàëåå: 1.2. 
Çàäà÷è äëÿ ñàìîñòîÿòåëüíîãî
Ââåðõ: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è
Íàçàä: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è

ßÃÏÓ, Öåíòð èíôîðìàöèîííûõ
òåõíîëîãèé îáó÷åíèÿ

2005-09-21

Источник

Далее: 8.  Задачи для самостоятельного
Вверх: Методическое пособие
Назад: 6.  Молекулярная физика

7.  Примеры решения задач

Пример 7.3. Сжиженные газы хранят в сосудах, сообщающихся с атмосферой. Можно ли
допустить испарение жидкого азота объемом
$displaystyle{0,5,{text{л}}}$
и плотностью

$displaystyle{0,81,{text{г/см}}^3}$
в закрытом сосуде объемом
$displaystyle{10,{text{л}}}$
при нагревании
его до температуры
$displaystyle{20^circ C}$
, если стенки сосуда выдерживают давление

$displaystyle{20,{text{атм}}}$
?

Дано:

$displaystyle{V_1=0,5,{text{л}}=5cdot 10^{-4},{text{м}}^3}$
$displaystyle{rho_1=0,81,{text{г/см}}^3=810,{text{кг/м}}^3}$
$displaystyle{V=10,{text{л}}=10^{-2},{text{м}}^3}$
$displaystyle{T=293,{text{К}}}$
$displaystyle{P=2cdot 10^6,{text{Па}}}$
 

$displaystyle{P_x}$
– ?

Решение.
При повышении температуры жидкий азот перейдет в газообразное состояние.
Примем его при температуре
$displaystyle{20^circ C}$
за идеальный газ и применим для решения
уравнение Клапейрона – Менделеева:

begin{equation}
PV = {movermu}RT,,
end{equation}


где
$displaystyle{P}$
,
$displaystyle{V}$
и
$displaystyle{T}$
– давление, объем и температура газа;
$displaystyle{m}$
– его масса,
$displaystyle{mu}$
– масса
моля азота, равная
$displaystyle{28cdot 10^{-3},{text{кг/моль}}}$
;
$displaystyle{R}$
– универсальная газовая постоянная.

Для ответа на вопрос задачи нужно определить давление газообразного азота и сравнить его с
максимально допустимым.

Выразим искомое давление из уравнения (26):

begin{equation}
P_x = {mRTovermu V},,
end{equation}


здесь неизвестна масса газа, ее можно определить через объем и плотность жидкого азота:

$displaystyle{m= rho_1V_1}$
. Выражение для искомого давления в общем виде:

begin{equation}
P_x = {rho_1V_1RTovermu V},.
end{equation}


Проверка наименования единицы искомой величины:

begin{equation}
[P_x]={{text{кг}}cdot{text{м}}^3cdot{text{Дж}}cdot{text{К}}cdot{text{моль}}over {text{м}}^3
cdot{text{моль}}cdot{text{К}}cdot{text{кг}}cdot{text{м}}^3}={{text{Дж}}over{text{м}}^3}=
{{text{Н}}cdot{text{м}}over{text{м}}^3}={{text{Н}}over{text{м}}^2}={text{Па.}}
end{equation}


Это единица давления в СИ, следовательно, выражение в общем виде получено правильно.

Вычисления: подставим числа (все они должны быть выражены в СИ):

Читайте также:  Спазм сосудов после курения

begin{equation}
P_x={8,1cdot 10^2cdot 5cdot 10^{-4}cdot 8,3 cdot 293over 28cdot 10^{-3}cdot
10^{-2}},{text{Па}},.
end{equation}


Прежде чем вычислять, проведем действия со степенями:

begin{equation}
P_x={8,1cdot 5cdot 8,3 cdot 293over 28}cdot 10^{3},{text{Па}}=3,52cdot
10^{6},{text{Па}},.
end{equation}


Искомое давление равно
$displaystyle{3,52cdot 10^6,{text{Па}}}$
или
$displaystyle{35,2 {text{атм}}}$
и превышает
допустимое.

Ответ: испарение жидкого азота данной массы в закрытом сосуде указанного объема нельзя
допустить, так как при
$displaystyle{20^circ ,С}$
давление превысит допустимое. Поэтому сжиженные газы хранят
в открытых сосудах.

Пример 7.4. Расстояние между стенками сосуда равно
$displaystyle{ 8 ,{text{мм}} }$
. При каком давлении вязкость
газа, находящегося между ними, начнет уменьшаться при откачке? Температура газа равна

$displaystyle{17^circ C}$
. Диаметр молекулы составляет
$displaystyle{3cdot 10^{-10},{text{м}}}$
.

Дано:

$displaystyle{ell=8cdot 10^{-3},{text{м}}}$
$displaystyle{T=290,K}$
$displaystyle{d=3cdot 10^{-10},{text{м}}}$
 

$displaystyle{P}$
– ?

Решение.
Теоретически вязкость газа при не слишком низких давлениях
не зависит от него:

begin{equation}
eta = {1over 3}overline{v}overline{lambda}rho,,
end{equation}



так как
$displaystyle{overline{lambda}}$
– средняя длина свободного пробега молекул обратно
пропорциональна давлению при постоянной температуре:

begin{equation}
overline{lambda} = {1over sqrt{2}pi d^2n}={kTover sqrt{2}pi d^2P},,
end{equation}


а плотность газа
$displaystyle{rho}$
прямо пропорциональна давлению. Выражение для плотности идеального газа
можно получить из уравнения Клапейрона – Менделеева:
$displaystyle{PV = {movermu}RT}$
, учитывая,
что плотность – это масса единицы объема:
$displaystyle{rho = {mover V}}$
. Получается, что

$displaystyle{rho = {mu Pover RT}}$
.

При низком давлении средняя длина свободного пробега перестает
зависеть от давления и определяется размерами сосуда:

begin{equation}
overline{lambda} = ell,.
end{equation}


Молекулы движутся от стенки к стенке, не сталкиваясь между собой. Вязкость газа начнет
уменьшаться при дальнейшей откачке сосуда за счет уменьшения концентрации молекул
(плотности газа).

Для решения задачи нужно приравнять выражение для средней длины свободного
пробeгa молекул
$displaystyle{overline{lambda}}$
расстоянию между стенками сосуда:

begin{equation}
ell = {kTover sqrt{2}pi d^2P},
end{equation}



и выразить давление. Получаем:

begin{equation}
P = {kTover sqrt{2}pi d^2ell},.
end{equation}


В этом выражении для давления все известно.

Проверка наименования единицы измерения:

begin{equation}
[P]={{text{Дж}}cdot{text{К}}over{text{К}}cdot{text{м}}^2cdot{text{м}}}={{text{Дж}}over
{text{м}}^3}={{text{Н}}cdot{text{м}}over{text{м}}^3}={{text{Н}}over{text{м}}^2}={text{Па}},.
end{equation}


Выражение для давления в общем виде получено правильно.

Вычисления:

begin{equation}
P={1,38cdot 10^{-23}cdot 290over sqrt{2}cdot 3,14cdot 9cdot 10^{-20}cdot 8cdot
10^{-3}},{text{Па}}={1,38cdot 290over sqrt{2}cdot 3,14cdot 9cdot 8},{text{Па}}=1,26,
{text{Па}},.
end{equation}


Полученное число значительно меньше величины атмосферного давления. Для данного газа при неизменной
температуре оно определяется только размерами сосуда
$displaystyle{ell}$
.

Ответ: при давлении 1,26 Па вязкость газа начнет уменьшаться при откачке.
Указание: подобным образом решаются задачи, связанные с коэффициентом теплопроводности
идеального газа:

begin{equation}
chi = {1over 3}overline{v}overline{lambda}rho c_v,,
end{equation}



где
$displaystyle{c_v}$
– удельная теплоемкость
при постоянном объеме:

begin{equation}
c_v={iover 2}{Rovermu} (i{text{ – – – число степеней свободы молекулы}}).
end{equation}


Пример 7.5. 10 л азота, находящегося под давлением
$displaystyle{10^5,{text{Па}}}$
, расширяются вдвое.
Найти конечное давление и совершенную газом работу в случаях изобарического,
изотермического и адиабатического процессов. Молекулы азота имеют пять степеней свободы.

Дано:

$displaystyle{P_1=10^{5},{text{Па}}}$
;
$displaystyle{V_1=10^{-2},{text{м}}^3}$
;
$displaystyle{V_2=2cdot 10^{-2}, {text{м}}^3}$
;
$displaystyle{i=5}$
 

$displaystyle{P_2}$
– ?
$displaystyle{A}$
– ?

Решение.
Примем азот в данных условиях за идеальный газ.

1. При изобарическом процессе давление газа не меняется, поэтому
$displaystyle{P_2=P_1}$
.
Элементарная работа расширения равна в общем случае
$displaystyle{PdV}$
, где
$displaystyle{P}$
– давление,

$displaystyle{dV}$
– бесконечно малый объем. Полная работа находится путем интегрирования, и величина
eе зависит от вида процесса.

При изобарическом процессе

begin{equation}
A_1=intlimits_{V_1}^{V_2}{PdV}=P(V_2-V_1),.
end{equation}


Проверим единицу измерения работы:

begin{equation}
[A] = {{text{Н}}cdot {text{м}}^3over {text{м}}^2}={text{Н}}cdot{text{м}}={text{Дж}},.
end{equation}


2. В изотермическом процессе температура остается постоянной, а давления и объемы в двух
состояниях идеального газа связаны законом Бойля – Мариотта:
$displaystyle{P_1V_1=P_2V_2}$
, откуда

$displaystyle{P_2’={P_1V_1over V_2}}$
. Видно, что здесь для единицы неизвестного давления получается
Па (паскаль).

Работа изотермического расширения рассчитывается так:

begin{equation}
A_2=int{PdV}=intlimits_{V_1}^{V_2}{{m over mu}RT{dVover V}}={movermu}RTln{V_2
over V_1},.
end{equation}


Здесь давление выражено из уравнения Клапейрона – Менделеева. Температура
неизвестна, поэтому, применив еще раз уравнение Клапейрона – Менделеева, получим выражение
для искомой работы через известные в условии величины:

begin{equation}
A_2 = P_1V_1ln{V_2over V_1},.
end{equation}


Результат не изменится, если подставить конечные давление и объем
$displaystyle{P_2}$
и

$displaystyle{V_2}$
или вместо отношения
$displaystyle{{V_2over V_1}}$
взять
$displaystyle{{P_1over P_2}}$
.

3. Конечное давление адиабатического ра

Предыдущая статья
Мрт головного мозга и сосудов головного мозга ...
Следующая статья
Оксид азота влияние на сосуды
© Про сосуды от врачей отеля