T найти концентрацию молекул газа в сосуде
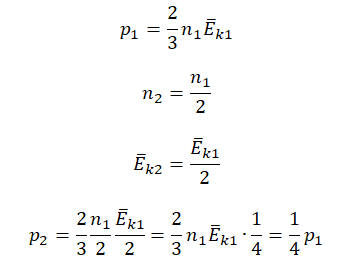
Задача по физике – 7136
Определить с помощью распределения Максвелла давление, оказываемое газом на стенку, если температура газа $T$ и концентрация молекул $n$.
Подробнее
Задача по физике – 7137
Воспользовавшись распределением Максвелла, найти $langle 1/v rangle$ – среднее значение обратной скорости молекул идеального газа, находящегося при температуре $T$, если масса каждой молекулы $m$. Сравнить полученную величину с обратной величиной средней скорости.
Подробнее
Задача по физике – 7138
Газ состоит из молекул массы $m$ и находится при температуре $T$. Найти с помощью распределения Максвелла по скоростям $v$ соответствующее распределение молекул по кинетическим энергиям $epsilon$. Определить наиболее вероятное значение кинетической энергии $epsilon_{вер}$. Соответствует ли $epsilon_{вер}$ наиболее вероятной скорости?
Подробнее
Задача по физике – 7139
Какая часть одноатомных молекул газа, находящегося в тепловом равновесии, имеет кинетическую энергию, отличающуюся от ее среднего значения на $delta eta = 1,0$%?
Подробнее
Задача по физике – 7140
Какая часть молекул газа, находящегося при температуре $T$, имеет кинетическую энергию поступательного движения большую, чем $epsilon_{0}$, если $epsilon_{0} gg kT$?
Подробнее
Задача по физике – 7141
Распределение молекул по скоростям в пучке, выходящем из отверстия в сосуде, описывается функцией $F(v) = Av^{3}e^{- mv^{2}/2kT}$, где $T$ – температура газа внутри сосуда. Найти наиболее вероятные значения:
а) скорости молекул в пучке; сравнить полученную величину c наиболее вероятной скоростью молекул в самом сосуде;
б) кинетической энергии молекул в пучке.
Подробнее
Задача по физике – 7142
Идеальный газ, состоящий из молекул массы $m$ с концентрацией $n$, имеет температуру $T$. Найти с помощью распределения Максвелла число молекул, падающих в единицу времени на единицу поверхности стенки под углами $theta, theta + d theta$ к ее нормали.
Подробнее
Задача по физике – 7143
Исходя из условий задачи 7142, найти число молекул, падающих в единицу времени на единицу поверхности стенки со скоростями в интервале $v, v + dv$.
Подробнее
Задача по физике – 7144
Найти силу, действующую на частицу со стороны однородного поля, если концентрации этих частиц на двух уровнях, отстоящих друг от друга на расстоянии $Delta h = 3,0 см$ (вдоль поля), отличаются в $eta = 2,0$ раза. Температура системы $T = 280 К$.
Подробнее
Задача по физике – 7145
При наблюдении в микроскоп взвешенных частиц гуммигута обнаружено, что среднее число их в слоях, расстояние между которыми $h = 40 мкм$, отличается друг от друга в $eta = 2,0$ раза. Температура среды $T = 290 К$. Диаметр частиц $d = 0,40 мкм$ и их плотность на $Delta rho = 0,20 г/см^{3}$ больше плотности окружающей жидкости. Найти по этим данным число Авогадро.
Подробнее
Задача по физике – 7146
Пусть $eta_{0}$ – отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, a $eta$ – соответствующее отношение на высоте $h = 3000 м$. Найти отношение $eta / eta_{0}$ при $T = 280 К$, полагая, что температура и ускорение, свободного падения не зависят от высоты.
Подробнее
Задача по физике – 7147
В длинном вертикальном сосуде находится газ, состоящий из двух сортов молекул с массами $m_{1}$ и $m_{2}$, причем $m_{2} > m_{1}$. Концентрации этих молекул у дна сосуда равны соответственно $n_{1}$ и $n_{2}$, причем гц > nt. Считая, что по всей высоте поддерживается одна и та же температура $T$ и ускорение свободного падения равно $g$, найти высоту $h$, на которой концентрации этих сортов молекул будут одинаковы.
Подробнее
Задача по физике – 7148
В очень высоком вертикальном цилиндрическом сосуде находится углекислый газ при некоторой температуре $T$. Считая поле тяжести однородным, найти, как изменится давление газа на дно сосуда, если температуру газа увеличить в $eta$ раз.
Подробнее
Задача по физике – 7149
Газ находится в очень высоком цилиндрическом сосуде при температуре $T$. Считая поле тяжести однородным, найти среднее значение потенциальной энергии молекул газа. Как зависит эта величина от того, состоит ли газ из одного сорта молекул или из нескольких сортов?
Подробнее
Задача по физике – 7150
Закрытую с обоих торцов горизонтальную трубку длины $l = 100 см$ перемещают с постоянным ускорением $w$, направленным вдоль ее оси. Внутри трубки находится аргон при температуре $T = 330 К$. При каком значении $w$ концентрации аргона вблизи торцов трубки будут отличаться друг от друга на $eta = 1,0$%?
Подробнее
Источник
Определение
Идеальный газ – газ, удовлетворяющий трем условиям:
- Молекулы – материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль – температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия – t. Единица измерения – 1 градус Цельсия (1 oC).
- По шкале Кельвина – T. Единица измерения – 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p – давление идеального газа, n – концентрация молекул газа, −Ek – средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
p=13m0n−v2 | m0- масса одной молекулы газа; n – концентрация молекул газа; −v2 – среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
p=13ρ−v2 | ρ – плотность газа |
p=nkT | k – постоянная Больцмана (k = 1,38∙10-3 Дж/кг) T – температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R – универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура – мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
Следовательно:
Составим систему уравнений:
Отсюда:
Задание EF19012 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева – Клапейрона выяснить, как меняются указанные физические величины во время процессов 1-2 и 2-3.
Решение
График построен в координатах (V;Ek). Процесс 1-2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева – Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1-2 является изобарным, давление во время него не меняется.
Процесс 2-3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2-3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление – обратно пропорциональные величины, то давление на участке 2-3 увеличивается.
Ответ:
• Участок 1-2 – изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2-3 – изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18416 Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18824 В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF | Просмотров: 1.7k | Оценить:
Источник
