Температура в закрытых сосудах

Главная Онлайн учебники База репетиторов России Тренажеры по физике Подготовка к ЕГЭ 2017 онлайн
Глава 3. Молекулярная физика и термодинамика
Молекулярно-кинетическая теория
3.4. Испарение, конденсация, кипение. Насыщенные и ненасыщенные пары
Любое вещество при определенных условиях может находиться в различных агрегатных состояниях – твердом, жидком и газообразном. Переход из одного состояния в другое называется фазовым переходом. Испарение и конденсация являются примерами фазовых переходов.
Все реальные газы (кислород, азот, водород и т. д.) при определенных условиях способны превращаться в жидкость. Однако такое превращение может происходить только при температурах ниже определенной, так называемой критической температуры Tкр. Например, для воды критическая температура равна 647,3 К, для азота 126 К, для кислорода 154,3 К. При комнатной температуре (≈ 300 К) вода может находиться и в жидком, и в газообразном состояниях, а азот и кислород существуют только в виде газов.
Испарением называется фазовый переход из жидкого состояния в газообразное. С точки зрения молекулярно-кинетической теории, испарение – это процесс, при котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, т. е. к охлаждению жидкости (если нет подвода энергии от окружающих тел).
Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость.
 |
Модель. Испарение и конденсация |
В закрытом сосуде жидкость и ее пар могут находиться в состоянии динамического равновесия, когда число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара, т. е. когда скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.
Число молекул, вылетающих с единицы площади поверхности жидкости за одну секунду, зависит от температуры жидкости. Число молекул, возвращающихся из пара в жидкость, зависит от концентрации молекул пара и от средней скорости их теплового движения, которая определяется температурой пара. Отсюда следует, что для данного вещества концентрация молекул пара при равновесии жидкости и ее пара определяется их равновесной температурой. Установление динамического равновесия между процессами испарения и конденсации при повышении температуры происходит при более высоких концентрациях молекул пара. Так как давление газа (пара) определяется его концентрацией и температурой, то можно сделать вывод: давление насыщенного пара p0 данного вещества зависит только от его температуры и не зависит от объема. Поэтому изотермы реальных газов на плоскости (p, V) содержат горизонтальные участки, соответствующие двухфазной системе (рис. 3.4.1).
| Рисунок 3.4.1. Изотермы реального газа. Область I – жидкость, область II – двухфазная система «жидкость + насыщенный пар», область III – газообразное вещество. K – критическая точка |
При повышении температуры давление насыщенного пара и его плотность возрастают, а плотность жидкости уменьшается из-за теплового расширения. При температуре, равной критической температуре Tкр для данного вещества, плотности пара и жидкости становятся одинаковыми. При T > Tкр исчезают физические различия между жидкостью и ее насыщенным паром.
Если изотермически сжимать ненасыщенный пар при T < Tкр, то его давление будет возрастать, пока не станет равным давлению насыщенного пара. При дальнейшем уменьшении объема на дне сосуда образуется жидкость и устанавливается динамическое равновесие между жидкостью и ее насыщенным паром. С уменьшением объема все большая часть пара конденсируется, а его давление остается неизменным (горизонтальный участок на изотерме). Когда весь пар превращается в жидкость, давление резко возрастает при дальнейшем уменьшении объема вследствие малой сжимаемости жидкости.
Из газообразного состояния в жидкое можно перейти, минуя двухфазную область. Для этого нужно совершить процесс в обход критической точки K. Один из возможных процессов такого рода показан на рис. 3.4.1 ломаной линией ABC.
 |
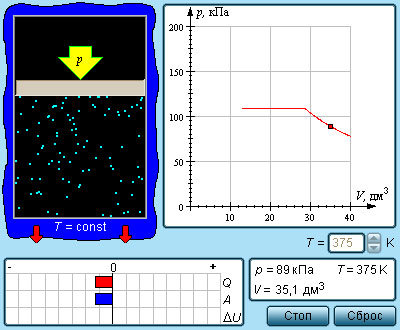
Модель. Изотермы реального газа |
В атмосферном воздухе всегда присутствуют пары воды при некотором парциальном давлении p, которое, как правило, меньше давления насыщенного пара p0. Отношение p / p0, выраженное в процентах, называется относительной влажностью воздуха.
Ненасыщенный пар можно теоретически описывать с помощью уравнения состояния идеального газа при обычных для реальных газов ограничениях: давление пара должно быть не слишком велико (практически p ≤ (106-107) Па), а его температура выше некоторого определенного для каждого вещества значения. К насыщенному пару также можно приближенно применять законы идеального газа при условии, что для каждой температуры T давление p0 насыщенного пара определяется по кривой равновесия p0(T) для данного вещества.
Давление p0 насыщенного пара очень быстро возрастает с ростом температуры T. Зависимость p0 (T) нельзя получить из законов идеального газа. Давление газа при постоянной концентрации молекул растет прямо пропорционально температуре. В насыщенном паре при повышении температуры возрастает не только средняя кинетическая энергия движения молекул, но и их концентрация. Поэтому давление насыщенного пара при повышении температуры возрастает быстрее, чем давление идеального газа при постоянной концентрации молекул.
Испарение может происходить не только с поверхности, но и в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа. Если давление насыщенного пара жидкости равно внешнему давлению (т. е. давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.
В частности, при нормальном атмосферном давлении вода кипит при температуре 100 °С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм. При подъеме в горы атмосферное давление уменьшается, и поэтому температура кипения воды понижается (приблизительно на 1 °С на каждые 300 метров высоты). На высоте 7 км давление составляет примерно 0,4 атм, и температура кипения понижается до 70 °С.
В герметически закрытом сосуде жидкость кипеть не может, т. к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром. По кривой равновесия p0 (T) можно определять температуру кипения жидкости при различных давлениях.
Изображенная на рис. 3.4.1 картина изотерм реального газа описывает процессы испарения и конденсации, т. е. фазовый переход между газообразной и жидкой фазами вещества. На самом деле эта картина является неполной, т. к. из газообразного и жидкого любое вещество может перейти в твердое состояние. При заданной температуре T термодинамическое равновесие между двумя фазами одного и того же вещества возможно лишь при определенном значении давления в системе. Зависимость равновесного давления от температуры называется кривой фазового равновесия. Примером может служить кривая равновесия p0 (T) насыщенного пара и жидкости. Если кривые равновесия между различными фазами данного вещества построить на плоскости (p, T), то они разбивают эту плоскость на отдельные области, в которых вещество существует в однородном агрегатном состоянии – твердом, жидком или газообразном (рис. 3.4.2). Изображенные в координатной системе (p, T) кривые равновесия называются фазовой диаграммой.
| Рисунок 3.4.2. Типичная фазовая диаграмма вещества. K – критическая точка, T – тройная точка. Область I – твердое тело, область II – жидкость, область III – газообразное вещество |
Кривая 0T, соответствующая равновесию между твердой и газообразной фазами, называется кривой сублимации. Кривая TK равновесия между жидкостью и паром называется кривой испарения, она обрывается в критической точке K. Кривая TM равновесия между твердым телом и жидкостью называется кривой плавления.
Кривые равновесия сходятся в точке T, в которой могут сосуществовать в равновесии все три фазы. Эта точка называется тройной точкой.
Для многих веществ давление pтр в тройной точке меньше 1 атм ≈ 105 Па. Такие вещества при нагревании при атмосферном давлении плавятся. Например, тройная точка воды имеет координаты Tтр = 273,16 К, pтр = 6,02·102 Па и используется в качестве опорной для калибровки абсолютной температурной шкалы Кельвина (см. §3.2). Существуют, однако, и такие вещества, у которых pтр превышает 1 атм. Так для углекислоты (CO2) давление pтр = 5,11 атм и температура Tтр = 216,5 К. Поэтому при атмосферном давлении твердая углекислота может существовать только при низкой температуре, а в жидком состоянии при p = 1 атм она вообще не существует. В твердом состоянии в равновесии со своим паром при атмосферном давлении углекислота находится при температуре 173 К или -80 °С. Это широко применяемый «сухой лед», который никогда не плавится, а только испаряется (сублимирует).
Источник
“…56. Температура стенки допустимая максимальная (минимальная) – максимальная (минимальная) температура стенки, при которой допускается эксплуатация сосуда…”
Источник:
Постановление Госатомнадзора РФ N 2, Госгортехнадзора РФ N 99 от 19.06.2003 “Об утверждении и введении в действие федеральных норм и правил в области использования атомной энергии “Правила устройства и безопасной эксплуатации сосудов, работающих под давлением, для объектов использования атомной энергии. НП-044-03” (Зарегистрировано в Минюсте РФ 10.07.2003 N 4886)
Официальная терминология. Академик.ру. 2012.
Смотреть что такое “Допустимая температура стенки сосуда” в других словарях:
допустимая температура стенки максимальная – Максимальная температура стенки, при которой допускается эксплуатация сосуда [ПБ 03 576 03] Тематики сосуды, в т. ч., работающие под давлением … Справочник технического переводчика
допустимая температура стенки минимальная – Минимальная температура стенки, при которой допускается эксплуатация сосуда [ПБ 03 576 03] Тематики сосуды, в т. ч., работающие под давлением … Справочник технического переводчика
Температура стенки допустимая максимальная (минимальная) – 56. Температура стенки допустимая максимальная (минимальная) максимальная (минимальная) температура стенки, при которой допускается эксплуатация сосуда. Источник … Словарь-справочник терминов нормативно-технической документации
температура – 3.1 температура: Средняя кинетическая энергия частиц среды, обусловленная их разнонаправленным движением в среде, находящейся в состоянии термодинамического равновесия. Источник: ГОСТ Р ЕН 306 2011: Теплообменники. Измерения и точность измерений… … Словарь-справочник терминов нормативно-технической документации
ПБ 03-576-03: Правила устройства и безопасной эксплуатации сосудов, работающих под давлением – Терминология ПБ 03 576 03: Правила устройства и безопасной эксплуатации сосудов, работающих под давлением: 1. Армированные пластмассы материалнеоднородного строения, состоящий из пластмассы (связующего) и наполнителя. Определения термина из… … Словарь-справочник терминов нормативно-технической документации
давление – 2.3 давление: Механическая величина, характеризующая интенсивность сил, действующих на внутреннюю (внутреннее давление среды) или наружную (внешнее давление воды, грунта) поверхность трубопровода по нормали к ней. Источник: СТО Газпром 2 2.1 318… … Словарь-справочник терминов нормативно-технической документации
Давление условное – 7 . Давление условное рабочее давление среды в арматуре и деталях трубопроводов, при котором обеспечивается их длительная эксплуатация при 20 °С. Источник … Словарь-справочник терминов нормативно-технической документации
НП 044-03: Правила устройства и безопасной эксплуатации сосудов, работающих под давлением, для объектов использования атомной энергии – Терминология НП 044 03: Правила устройства и безопасной эксплуатации сосудов, работающих под давлением, для объектов использования атомной энергии: 1. Авария нарушение нормальной эксплуатации оборудования, применяемого на ОИАЭ, при котором… … Словарь-справочник терминов нормативно-технической документации
Временная методика. Экспертное техническое диагностирование сосудов, работающих под давлением на компрессорных и газораспределительных станциях. Оценка технического состояния и возможности дальнейшей эксплуатации – Терминология Временная методика. Экспертное техническое диагностирование сосудов, работающих под давлением на компрессорных и газораспределительных станциях. Оценка технического состояния и возможности дальнейшей эксплуатации: 3.13 А РД диаграмма … Словарь-справочник терминов нормативно-технической документации
Термос – Термосы для напитков со стеклянной колбой Термос вид бытовой теплоизоляционной посуды для продолжительного сохранения более высокой или низкой температуры … Википедия
Источник
Примеры решения задач по теме “Процессы изменения состояния идеальных газов”
1. В закрытом сосуде емкостью $V = 300$ л содержится $3$ кг газа при давлении $p_1 = 8$ ат и температуре $t_1 = 20$ °C. Определить давление (ат) и удельный объем после охлаждения воздуха до $0$ °C.

2. В закрытом сосуде заключен газ при разрежении $p_1 = 6.7$ кПа и температуре $t_1 = 70$ °C. Показания барометра – $742$ мм.рт.ст. До какой температуры нужно охладить газ при том же атмосферном давлении, чтобы разрежение стало $p_2 = 13.3$ кПа?

3. В закрытом сосуде емкостью $V = 0.6$ м3 содержится азот при давлении (абсолютном) $p_1 = 0.5$ МПа и температуре $t_1 = 20$ °C. В результате охлаждения сосуда азот, содержащийся в нем, теряет $105$ кДж. Определить, какие давление и температура устанавливаются в сосуде после охлаждения.

4. Сосуд емкостью $90$ л содержит углекислый газ при абсолютном давлении $0.8$ МПа и температуре $30$ °C. Определить количество теплоты, которое необходимо сообщить газу при $v = const$, чтобы давление поднялось до $1.6$ МПа.

5. Какое количество теплоты необходимо затратить, чтобы нагреть $2$ м3 воздуха при постоянном избыточном давлении $p = 2$ ат от $t_1 = 120$ °C до $t_2 = 450$ °C? Какую работу при этом совершит воздух? Атмосферное давление принять равным $750$ мм.рт.ст., учесть зависимость теплоемкости от температуры.

6. В установке воздушного отопления внешний воздух при $t_1 = – 15$ °C нагревается в калорифере при $p = const$ до $60$ °C. Какое количество теплоты надо затратить для нагревания $1000$ м3 наружного воздуха? Давление воздуха считать равным $755$ мм.рт.ст.

7. Уходящие газы котельной установки проходят через воздухоподогреватель. Начальная температура газов $t_{г1} = 300$ °C, конечная $t_{г2} = 160$ °C; расход газов равен $900$ кг/ч. Начальная температура воздуха составляет $t_{в1} = 15$ °C, а расход его равен $800$ кг/ч. Определить температуру нагретого воздуха $t_{в2}$, если потери тепла в воздухоподогревателе составляет $4$ %. Средние теплоемкости для газов и воздуха принять соответственно равными $1.0467$ и $1.0048$ кДж/(кгּ К).

8. При сжигании в топке парового котла каменного угля объем продуктов сгорания составляет $V_н = 11.025$ м3/кг (объем при нормальных условиях, приходящийся на 1 кг топлива). Анализ продуктов сгорания показывает следующий их объемный состав: $CO = 10$ %; $O2 = 8$ %; $H2O = 10$ %; $N2 = 72$ %. Определить количество теплоты, теряемой с уходящими газами (в расчете на $1$ кг топлива), если на выходе из котла температура газов равна $180$ °C, а температура окружающей среды $20$ °C. Давление продуктов сгорания принять равным атмосферному. Учесть зависимость теплоемкости от температуры.

9. Воздух в количестве $1$ кг при температуре $t = 30$ °C и начальном давлении $p_1 = 0.1$ МПа изотермически сжимается до конечного давления $p_2 = 1$ МПа. Определить конечный объем, затрачиваемую работу изменения объема и количество теплоты, отводимой от газа.

10. Воздух в количестве $12$ кг при температуре $t = 27$ °C изотермически сжимается до тех пор, пока давление не становится равным $4$ МПа. На сжатие затрачивается работа $L = -6$ МДж. Найти начальные давление и объем, конечный объем и теплоту, отведенную от воздуха.

11. Воздух в количестве $0.5$ кг изотермически расширяется от давления $p_1 = 100$ ат до $p_2$. Определить давление $p_2$ в ат, работу изменения объема $L_{1-2}$ и отведенную теплоту $Q_{1-2}$, если $frac{v_2}{v_1} = 5$ и $t_1 = 30$ °C.

12. В идеально охлаждаемом компрессоре происходит изотермическое сжатие углекислого газа. В компрессор поступает $700$ м3/ч газа (приведенного к нормальным условиям) при $p_1 = 0.095$ МПа и $t_1 = 47$ °C. Давление за компрессором $p_2 = 0.8$ МПа. Найти теоретическую мощность приводного двигателя $N_0$ (кВт) и теоретический расход $M_в$ охлаждающей компрессор воды (в кг/ч), если она нагревается в системе охлаждения на $Δt = 15$ °C.

13. Воздух при температуре $t_1 = 20$ °C должен быть охлажден посредством адиабатного расширения до температуры $t_2 = -30$ °C. Конечное давление воздуха при этом должно составлять $0.1$ МПа. Определить начальное давление воздуха $p_1$ и работу расширения $1$ кг воздуха.

14. Воздух при температуре $120$ °C изотермически сжимается так, что его объем становится равным $0.25$ начального, а затем расширяется по адиабате до начального давления. Определить температуру воздуха в конце адиабатного расширения. Представить процессы расширения и сжатия в диаграммах pv и Ts.


15. При адиабатном расширении $1$ кг воздуха $K = 1.40 = сonst$ температура его падает на $100$ K. Какова полученная в процессе расширения работа и сколько теплоты следовало бы подвести к воздуху, чтобы ту же работу получить в изотермическом процессе?

16. Воздух в количестве $1$ кг политропно расширяется от $12$ до $2$ ат, причем объем его увеличился в $4$ раза; начальная температура воздуха равна $120$ °C. Определить показатель политропы, начальный и конечный объемы, конечную температуру и работу расширения.

17. При политропном сжатии $1$ кг воздуха до объема $v_2 = 0.1ּ v_1$ температура поднялась с $10$ до $90$ °C. Начальное давление равно $0.8$ бар; $R = 287$ Дж/(кгּ K). Определить показатель политропы, конечные параметры газа, работу сжатия и количество отведенной наружу теплоты.

18. Воздух в компрессоре сжимается по политропе $n = 1.25$ от $1$ до $8$ бар; начальная температура воздуха $5$ °C. После сжатия воздух проходит через холодильник, охлаждаемый холодной водой, начальная температура которой $t_1 = 10$ °C, а конечная равна $t_2 = 18$ °C. Определить часовой расход охлаждающей воды, если производительность компрессора $1000$ мн3/ч при нормальных физических условиях, а воздух в холодильнике изобарно охлаждается до $30$ °C.

19. В воздушном двигателе воздух в количестве $1$ кг расширяется от $p_1 = 10$ ат до $p_2 = 1$ ат. Расширение может произойти изотермически, адиабатно и политропно с показателем политропы $n = 1.2$. Сравнить работы расширения и определить конечные параметры воздуха по этим трем процессам; начальная температура воздуха $t_1 = 227$ °C. Представить процессы на диаграмме pv.


20. В процессе политропного расширения воздуху сообщается $70$ кДж теплоты. Найти изменение внутренней энергии воздуха и произведенную работу, если объем воздуха увеличился в $8$ раз, а давление его уменьшилось в $10$ раз.

Источник
