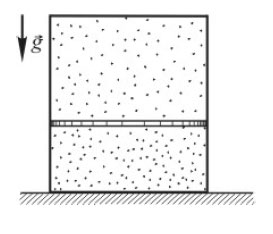
Теплоизолированный горизонтальный сосуд разделен
1. Так как сосуд теплоизолирован и начальные температуры газов одинаковы, то после установления равновесия температура в сосуде будет равна первоначальной, а гелий равномерно распределится по всему сосуду. После установления равновесия в системе в каждой части сосуда окажется по моль гелия: В результате в сосуде с аргоном окажется моль смеси:
2. Внутренняя энергия одноатомного идеального газа пропорциональна температуре и количеству молей:
3. Запишем условие термодинамического равновесия:
4.
Ответ:
Порядок назначения третьего эксперта
В соответствии с Порядком проведения государственной итоговой
аттестации по образовательным программам среднего общего образования
(приказ Минобрнауки России от
зарегистрирован
Минюстом России
)
« По результатам первой
и второй проверок эксперты независимо
друг от друга выставляют баллы за каждый ответ на задания
экзаменационной работы ЕГЭ с развёрнутым ответом…
В случае существенного расхождения в баллах, выставленных
двумя экспертами, назначается третья проверка. Существенное расхождение
в баллах определено в критериях оценивания по соответствующему
учебному предмету.
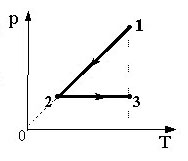
Эксперту, осуществляющему третью проверку, предоставляется
информация о баллах, выставленных экспертами, ранее проверявшими
экзаменационную работу».
Если расхождение составляет
и более балла за выполнение задания, то третий эксперт проверяет ответы только на то задание, которое
вызвало столь существенное расхождение.
Критерии оценки
3 баллаПриведено полное решение, включающее следующие элементы:
I. записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: формула для внутренней энергии одноатомного идеального газа, условие
термодинамического равновесия);
II. описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);
III. проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV. представлен правильный ответ
2 баллаПравильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в
записи единиц измерения величины)
1 баллПредставлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения данной задачи (или утверждение, лежащее в основе
решения), но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения
данной задачи (или в утверждении, лежащем в основе решения),
допущена ошибка, но присутствуют логически верные
преобразования с имеющимися формулами, направленные на
решение задачи
0 балловВсе случаи решения, которые не соответствуют вышеуказанным
критериям выставления оценок в балла
Источник
Задачи из ДЕМОВАРИАНТОВ (с решениями)
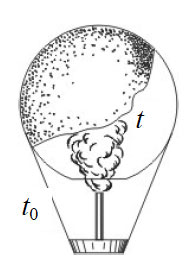
1. Воздушный шар, оболочка
которого имеет массу М = 145 кг и объем V =
230 м3, наполняется горячим воздухом при нормальном
атмосферном давлении и температуре окружающего воздуха tо
= 0оС. Какую минимальную температуру t должен
иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка
шара нерастяжима и имеет в нижней части небольшое отверстие.
Образец возможного решения
2. Воздушный
шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием.
Он может удерживать в воздухе на высоте, где температура воздуха
17оС, а давление 105 Па, груз массой 225
кг. Какова масса гелия в оболочке шара? Считать, что оболочка
шара не оказывает сопротивления изменению объема шара.
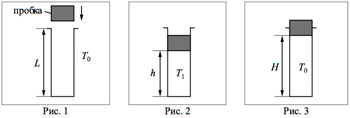
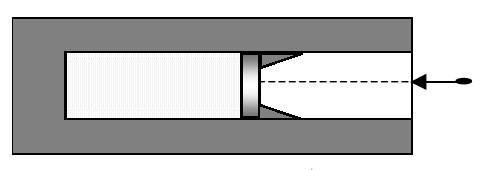
Образец возможного решения2*. В камере, заполненной азотом, при температуре T = 300 К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда L = 50 см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры T1. В результате расстояние от дна сосуда до низа пробки становится равным h = 40 см (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T0. Расстояние от дна сосуда до низа пробки при этой температуре становится равным H = 46 см (см. рис. 3). Чему равна температура T1? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь. Давление азота в камере во время эксперимента поддерживается постоянным.
Образец возможного решения
3. В медный
стакан калориметра массой 200 г, содержащий 150 г воды, опустили
кусок льда, имевший температуру 0°С. Начальная температура калориметра
с водой 25°С. В момент времени, когда наступит тепловое равновесие,
температура воды и калориметра стала равной 5°С. Рассчитайте массу
льда. Удельная теплоемкость меди 390 Дж/кг•К, удельная теплоемкость
воды 4200 Дж/кг•К, удельная теплота плавления льда 3,35•105
Дж/кг. Потери тепла калориметром считать пренебрежимо малыми.
Образец возможного решения4. Необходимо расплавить лёд массой 0,2 кг,
имеющий температуру 0оС. Выполнима ли эта задача,
если потребляемая мощность нагревательного элемента – 400 Вт,
тепловые потери составляют 30%, а время работы нагревателя не
должно превышать 5 минут?
Образец возможного решения4*. Теплоизолированный горизонтальный сосуд разделён пористой перегородкой на две равные части. В начальный момент в левой части сосуда находится ν = 2 моль гелия, а в правой – такое же количество моль аргона. Атомы гелия могут проникать через перегородку, а для атомов аргона перегородка непроницаема. Температура гелия равна температуре аргона: Т = 300 К. Определите отношение внутренних энергий газов по разные стороны перегородки после установления термодинамического равновесия.
Образец возможного решения4**. Теплоизолированный цилиндр разделён подвижным теплопроводным поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К, а аргона – 900 К; объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Поршень медленно перемещается без трения. Теплоёмкость поршня и цилиндра пренебрежимо мала. Чему равно отношение внутренней энергии гелия после установления теплового равновесия к его энергии в начальный момент?
Образец возможного решения
5. В вакууме
закреплен горизонтальный цилиндр с поршнем. В цилиндре находится
0,1 моль гелия. Поршень удерживается упорами и может скользить
влево вдоль стенок цилиндра без трения. В поршень попадает пуля
массой 10 г, летящая горизонтально со скоростью 400 м/с, и застревает
в нем. Температура гелия в момент остановки поршня в крайнем левом
положении возрастает на 64 К. Какова масса поршня? Считать, что
за время движения поршня газ не успевает обменяться теплом с поршнем
и цилиндром.
Образец возможного решения6. В горизонтальном цилиндрическом сосуде,
закрытом поршнем, находится одноатомный идеальный газ. Первоначальное
давление газа p1 = 4•105
Па. Расстояние от дна сосуда до поршня равно L. Площадь
поперечного сечения поршня S = 25 см2. В
результате медленного нагревания газ получил количество теплоты
Q = 1,65 кДж, а поршень сдвинулся на расстояние x
= 10 см. При движении поршня на него со стороны стенок сосуда
действует сила трения величиной Fтр = 3•103
Н. Найдите L. Считать, что сосуд находится в вакууме.
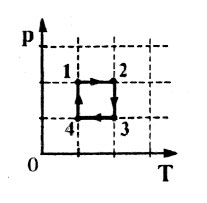
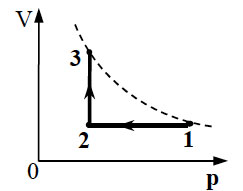
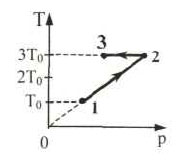
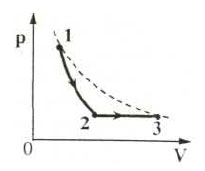
Образец возможного решения7. На pT-диаграмме показан
цикл тепловой машины, у которой рабочим телом является идеальный
газ (см. рисунок). На каком из участков цикла 1 – 2, 2 – 3, 3
– 4, 4 – 1 работа газа наибольшая по модулю?
Образец возможного решения
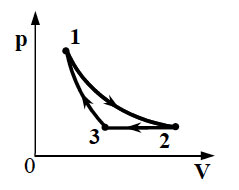
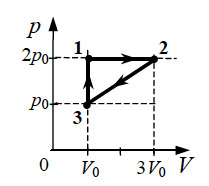
8. 10 моль одноатомного идеального
газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели
до первоначальной температуры 300 К (см. рисунок). Какое количество
теплоты получил газ на участке 2 – 3?
Образец возможного решения
9. 10 моль идеального одноатомного газа охладили,
уменьшив давление в 3 раза. Затем газ нагрели до первоначальной
температуры 300 К (см. рисунок). Какое количество теплоты сообщено
газу на участке 2 – 3?
Образец возможного решения
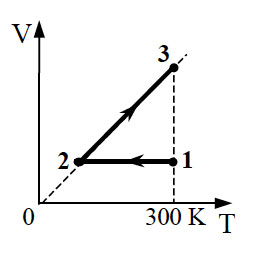
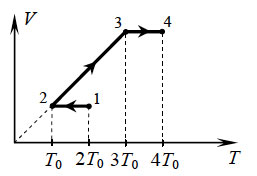
10. 1 моль идеального одноатомного газа сначала
охладили, а затем нагрели до первоначальной температуры 300
К, увеличив объем газа в 3 раза (см. рисунок). Какое количество
теплоты отдал газ на участке 1 – 2?
Образец возможного решения
10*. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
Образец возможного решения
11. Рассчитайте КПД тепловой
машины, использующей в качестве рабочего тела одноатомный идеальный
газ и работающей по циклу, изображенному на рисунке.
Образец возможного решения
Избранные задачи прошлых лет (с ответами)
12. Вертикально расположенный
замкнутый цилиндрический сосуд высотой 50 см разделен подвижным
поршнем весом 110 Н на две части, в каждой из которых содержится
одинаковое количество идеального газа при температуре 361 К. Сколько
молей газа находится в каждой части цилиндра, если поршень находится
на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
13. В калориметре
находился лед при температуре t1 = – 5 °С.
Какой была масса m1 льда, если после добавления
в калориметр m2 = 4 кг воды, имеющей температуру
t2 = 20 °С, и установления теплового равновесия
температура содержимого калориметра оказалась равной t
= 0 °С, причем в калориметре была только вода?14. Теплоизолированный
цилиндр разделен подвижным теплопроводным поршнем на две части.
В одной части цилиндра находится гелий, а в другой — аргон. В
начальный момент температура гелия равна 300 К, а аргона — 900
К. При этом объемы, занимаемые газами одинаковы. Какую температуру
будут иметь газы в цилиндре после установления теплового равновесия,
если поршень перемещается без трения? Теплоемкостью сосуда и поршня
пренебречь.15. Теплоизолированный
сосуд объемом V = 2 м3 разделен теплопроводящей
перегородкой на две части одинакового объема. В одной части находится
m = 1 кг гелия, а в другой части m = 1 кг аргона.
Средняя квадратичная скорость атомов аргона равна средней квадратичной
скорости атомов гелия и составляет υ = 500 м/с. Рассчитайте
парциальное давление гелия после удаления перегородки.16. Теплоизолированный
сосуд объемом V = 2 м3 разделен пористой перегородкой
на две равные части. В начальный момент в одной части сосуда находится
νHe = 2 моль гелия, а в другой – νAr
= 1 моль аргона. Температура гелия ТHe = 300
К, а температура аргона ТAr = 600 К. Атомы
гелия могут свободно проникать через поры в перегородке, а атомы
аргона – нет. Определите температуру гелия после установления
теплового равновесия в системе.17. С одним молем идеального
одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке
в координатах V-Т. Во сколько раз количество теплоты,
полученное газом в процессе 1-2-3-4 больше работы газа в этом
процессе?
18. Один моль одноатомного
идеального газа совершает процесс 1-2-3 (см. рисунок). На участке
2 – 3 к газу подводят 3 кДж теплоты. Т0 =
100 К. Найдите отношение работы, совершаемой газом в ходе всего
процесса А123, к соответствующему полному
количеству подведенной к нему теплоты Q123.
19. Один моль идеального
одноатомного газа сначала изотермически сжали (Т1
= 300 К). Затем газ изохорно охладили, понизив давление в 3 раза
(см. рисунок). Какое количество теплоты отдал газ на участке 2
– 3?
20. Идеальный одноатомный
газ расширяется сначала адиабатно, а затем изобарно. Конечная
температура газа равна начальной (см. рисунок). За весь процесс
1-2-3 газом совершается работа, равная 5 кДж. Какую работу совершает
газ при адиабатном расширении?
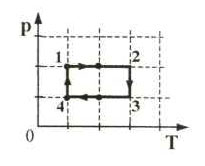
21. На рисунке в координатах
p,T показан цикл тепловой машины, у которой
рабочим телом является идеальный газ. На каком участке цикла работа
газа наименьшая по модулю?
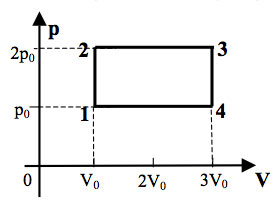
22. Один моль одноатомного
идеального газа совершает цикл, изображенный на pV-диаграмме
(см. рисунок). Участок 1 – 2 –– изотерма, 2 – 3 –– изобара, 3
– 1 –– адиабата. Работа, совершаемая газом за цикл, равна А.
Разность температур в состояниях 1 и 3 составляет ΔТ.
Какую работу совершает газ при изотермическом процессе?
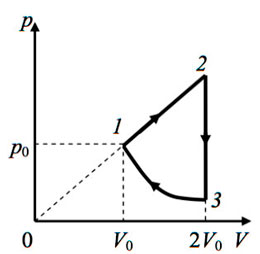
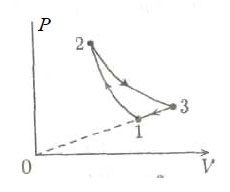
23. Газообразный гелий находится
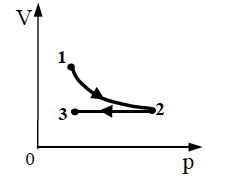
в цилиндре под подвижным поршнем. Газ сжимают в адиабатическом
процессе, переводя его из состояния 1 в состояние 2 (см. рис.).
Над газом совершается при этом работа сжатия А12
(А12> 0). Затем газ расширяется в изотермическом
процессе 2-3, и, наконец, из состояния 3 газ переводят в состояние
1 в процессе, когда его давление Р прямо пропорционально
объему V. Найти работу А23, которую
совершил газ в процессе изотермического расширения, если во всем
замкнутом цикле 1-2-3-1 он совершил работу А.
24. Температура
гелия увеличилась в k = 3 раза в процессе P2V
= const (Р — давление, V — объем газа), а его
внутренняя энергия изменилась на 100 Дж. Найти: 1) начальный объем
V1 газа; 2) начальное давление P1
газа. Максимальный объем, который занимал газ в процессе нагрева,
равнялся Vmax = 3 л.25. Одноатомный идеальный
газ неизменной массы совершает циклический процесс, показанный
на рисунке. За цикл от нагревателя газ получает количество теплоты
QH = 8 кДж. Чему равна работа газа за цикл?
Ответы к избранным задачам
прошлых лет
Источник
2017-05-27
Теплоизолированный сосуд, разделенный на две неравные части ($V_{1} = 2 л, V_{2} = 3 л$), наполнен идеальным газом. В первой части газ находится под давлением $p_{1} = 10^{5} Па$ при температуре $t_{1} = 27^{ circ} С$, во второй части — под давлением $p_{2} = 5 cdot 10^{5} Па$ и той же температуре (рис.). Найти изменение энтропии всей системы после удаления перегородки и установления равновесного состояния. Изменится ли ответ, если в объемах $V_{1}$ и $V_{2}$ находятся разные газы?
Решение:
Рассматриваемая система изолирована — теплообмен не происходит, внешние силы не действуют. После удаления перегородки начнется заведомо необратимый самопроизвольный процесс, в результате которого во всем сосуде будет находиться однородный газ под некоторым давлением $p_{0}$, причем $p_{1}
Энтропия системы в результате этого необратимого процесса увеличивается. Изменение ее определяется только начальным и конечным состояниями системы. Чтобы найти это изменение, надо представить себе любой обратимый процесс, переводящий данную систему из начального состояния в конечное.
Представим себе, что сосуды разделены поршнем, который перемещается до тех пор, пока давление с обеих его сторон не станет одинаковым и равным $p_{0}$ (газ в левой части сосуда сжимается, в правой расширяется). Чтобы процесс был изотермическим и обратимым, во-первых, должна быть нарушена теплоизоляция сосуда: газ в левой части сосуда должен отдавать теплоту, в правой — получать. Во-вторых, Рис. 63 поршень должен двигаться медленно, следовательно, на него должна действовать внешняя сила, компенсирующая результирующую силу давления газов.
После выравнивания давлений обе части газа окажутся в одинаковых равновесных состояниях; поэтому если убрать перегородку (поршень), то энтропия системы не изменится. Следовательно, искомое изменение энтропии системы равно сумме изменений энтропии каждой части газа в отдельности при описанном изотермическом перемещении поршня:
$Delta S = Delta S_{1} + Delta S_{2} = int_{p_{1}}^{ p_{0}} frac{ delta Q}{T} + int_{p_{2}}^{p_{0}} frac{ delta Q}{T}$. (1)
При изотермическом процессе
$delta Q_{T} = delta A_{T} = pdV = – V dp$.
[Последнее из равенств следует из того, что $d(pV) = 0$ при $pV = const$.] Тогда из уравнения (1)
$Delta S = frac{1}{T_{1}} left ( int_{p_{0}}^{p_{1}} Vdp + int_{p_{0}}^{p_{2}} Vdp right )$.
Выражая в интегралах текущий объем $V$ из уравнений изотермических процессов, записанных для начального и текущего состояний, получим
$Delta S = frac{1}{T_{1}} left ( int_{p_{0}}^{p_{1}} frac{p_{1}V_{1}}{p} dp + int_{p_{0}}^{p_{2}} frac{p_{2}V_{2}}{p} dp right ) = frac{1}{T_{1}} left ( p_{1}V_{1} ln frac{p_{1}}{p_{0}} + p_{2}V_{2} ln frac{p_{2}}{p_{0}} right )$. (2)
Давление $p_{0}$ может быть найдено из уравнений изотермических процессов для каждой части газа:
$p_{1}V_{1} = p_{0}V_{1}^{ prime}, p_{2}V_{2} = p_{0}V_{2}^{ prime}$, (3)
где $V_{1}^{ prime}$ и $V_{2}^{ prime}$ — объемы каждой части газа после выравнивания давлений, причем $V_{1}^{ prime} + V_{2}^{ prime} = V_{1} + V_{2}$. Тогда почленное сложение уравнений (3) дает
$p_{1}V_{1} + p_{2}V_{2} = p_{0}(V_{1} + V_{2})$,
откуда
$p_{0} = frac{p_{1}V_{1} + p_{2}V_{2}}{V_{1} + V_{2}}$. (4)
Подставив выражение (4) в (2), находим
$Delta = frac{1}{T_{1}} left [ p_{1}V_{1} ln frac{p_{1}(V_{1} + V_{2})}{p_{1}V_{1} + p_{2}V_{2}} + p_{2}V_{2} ln frac{p_{2}(V_{1} + V_{2})}{p_{1}V_{1} + p_{2}V_{2}} right ]= 1,1 Дж/К$.
Если бы в объемах $V_{1}$ и $V_{2}$ находились разные газы, то после удаления перегородки, даже при условии, что по обе ее стороны газы находятся под одинаковым давлением $p_{0}$, начнется необратимый самопроизвольный процесс диффузии, который приведет к выравниванию концентраций каждого из газов во всем объеме сосуда. Очевидно, что в процессе диффузии энтропия будет возрастать. Следовательно, в этом случае полное изменение энтропии системы больше значения, найденного ранее.
Чтобы рассчитать изменение энтропии в процессе диффузии, надо заменить реальный необратимый процесс таким воображаемым обратимым процессом, который приведет систему в то же самое конечное состояние. Такой процесс может быть осуществлен только с помощью полупроницаемых перегородок, т. е. перегородок, проницаемых для молекул одного газа и непроницаемых для молекул другого газа.
Источник