Теплоизолированный сосуд разделен на две части поршнем
2017-05-27 
Теплоизолированный сосуд, разделенный на две неравные части ($V_{1} = 2 л, V_{2} = 3 л$), наполнен идеальным газом. В первой части газ находится под давлением $p_{1} = 10^{5} Па$ при температуре $t_{1} = 27^{ circ} С$, во второй части — под давлением $p_{2} = 5 cdot 10^{5} Па$ и той же температуре (рис.). Найти изменение энтропии всей системы после удаления перегородки и установления равновесного состояния. Изменится ли ответ, если в объемах $V_{1}$ и $V_{2}$ находятся разные газы?
Решение:
Рассматриваемая система изолирована — теплообмен не происходит, внешние силы не действуют. После удаления перегородки начнется заведомо необратимый самопроизвольный процесс, в результате которого во всем сосуде будет находиться однородный газ под некоторым давлением $p_{0}$, причем $p_{1}
Энтропия системы в результате этого необратимого процесса увеличивается. Изменение ее определяется только начальным и конечным состояниями системы. Чтобы найти это изменение, надо представить себе любой обратимый процесс, переводящий данную систему из начального состояния в конечное.
Представим себе, что сосуды разделены поршнем, который перемещается до тех пор, пока давление с обеих его сторон не станет одинаковым и равным $p_{0}$ (газ в левой части сосуда сжимается, в правой расширяется). Чтобы процесс был изотермическим и обратимым, во-первых, должна быть нарушена теплоизоляция сосуда: газ в левой части сосуда должен отдавать теплоту, в правой — получать. Во-вторых, Рис. 63 поршень должен двигаться медленно, следовательно, на него должна действовать внешняя сила, компенсирующая результирующую силу давления газов.
После выравнивания давлений обе части газа окажутся в одинаковых равновесных состояниях; поэтому если убрать перегородку (поршень), то энтропия системы не изменится. Следовательно, искомое изменение энтропии системы равно сумме изменений энтропии каждой части газа в отдельности при описанном изотермическом перемещении поршня:
$Delta S = Delta S_{1} + Delta S_{2} = int_{p_{1}}^{ p_{0}} frac{ delta Q}{T} + int_{p_{2}}^{p_{0}} frac{ delta Q}{T}$. (1)
При изотермическом процессе
$delta Q_{T} = delta A_{T} = pdV = – V dp$.
[Последнее из равенств следует из того, что $d(pV) = 0$ при $pV = const$.] Тогда из уравнения (1)
$Delta S = frac{1}{T_{1}} left ( int_{p_{0}}^{p_{1}} Vdp + int_{p_{0}}^{p_{2}} Vdp right )$.
Выражая в интегралах текущий объем $V$ из уравнений изотермических процессов, записанных для начального и текущего состояний, получим
$Delta S = frac{1}{T_{1}} left ( int_{p_{0}}^{p_{1}} frac{p_{1}V_{1}}{p} dp + int_{p_{0}}^{p_{2}} frac{p_{2}V_{2}}{p} dp right ) = frac{1}{T_{1}} left ( p_{1}V_{1} ln frac{p_{1}}{p_{0}} + p_{2}V_{2} ln frac{p_{2}}{p_{0}} right )$. (2)
Давление $p_{0}$ может быть найдено из уравнений изотермических процессов для каждой части газа:
$p_{1}V_{1} = p_{0}V_{1}^{ prime}, p_{2}V_{2} = p_{0}V_{2}^{ prime}$, (3)
где $V_{1}^{ prime}$ и $V_{2}^{ prime}$ — объемы каждой части газа после выравнивания давлений, причем $V_{1}^{ prime} + V_{2}^{ prime} = V_{1} + V_{2}$. Тогда почленное сложение уравнений (3) дает
$p_{1}V_{1} + p_{2}V_{2} = p_{0}(V_{1} + V_{2})$,
откуда
$p_{0} = frac{p_{1}V_{1} + p_{2}V_{2}}{V_{1} + V_{2}}$. (4)
Подставив выражение (4) в (2), находим
$Delta = frac{1}{T_{1}} left [ p_{1}V_{1} ln frac{p_{1}(V_{1} + V_{2})}{p_{1}V_{1} + p_{2}V_{2}} + p_{2}V_{2} ln frac{p_{2}(V_{1} + V_{2})}{p_{1}V_{1} + p_{2}V_{2}} right ]= 1,1 Дж/К$.
Если бы в объемах $V_{1}$ и $V_{2}$ находились разные газы, то после удаления перегородки, даже при условии, что по обе ее стороны газы находятся под одинаковым давлением $p_{0}$, начнется необратимый самопроизвольный процесс диффузии, который приведет к выравниванию концентраций каждого из газов во всем объеме сосуда. Очевидно, что в процессе диффузии энтропия будет возрастать. Следовательно, в этом случае полное изменение энтропии системы больше значения, найденного ранее.
Чтобы рассчитать изменение энтропии в процессе диффузии, надо заменить реальный необратимый процесс таким воображаемым обратимым процессом, который приведет систему в то же самое конечное состояние. Такой процесс может быть осуществлен только с помощью полупроницаемых перегородок, т. е. перегородок, проницаемых для молекул одного газа и непроницаемых для молекул другого газа.
Источник
Задача по физике – 617
Произведение давления таза на его объем ($pV$) не меняется с изменением объема при постоянной температуре, только если предположить, что газы, с которыми мы имеем дело, являются идеальными.
Определите, будет уменьшаться или увеличиваться произведение $pV$ при очень сильном сжатии газа, если не делать предположения об идеальности последнего.
Подробнее
Задача по физике – 618
Горизонтальный цилиндрический сосуд длиной $2l$ разделен тонким нетеплопроводящим поршнем на две равные части, в каждой из которых находится по $n$ молей идеального одноатомного газа при температуре $T$. Поршень прикреплен к торцам сосуда недеформированными пружинами жесткости $k$ каждая (рис.). Газу в правой части сообщили количество теплоты $Q$, в результате чего поршень сместился влево на расстояние $x=l/2$.
Определите количество теплоты $Q^{prime}$, отданное при температуре $T$ термостату, с которым газ в левой части все время находился в тепловом контакте.
Подробнее
Задача по физике – 619
Теплоизолированный сосуд разделен на две части нетеплопроводящим поршнем, который может перемещаться в сосуде без трения. В левой части сосуда содержится 1 моль идеального одноатомного газа, в правой – вакуум. Поршень соединен с правой стенкой сосуда пружиной, длина которой в свободном состоянии равна длине сосуда (рис.).
Определите теплоемкость $C$ системы. Теплоемкостью сосуда, поршня и пружины пренебречь.
Подробнее
Задача по физике – 620
Докажите, что к. п. д. тепловой машины, использующей цикл, состоящий из двух изотерм и двух изохор, меньше к. п. д. идеальной тепловой машины Карно, работающей с теми же нагревателем и холодильником.
Подробнее
Задача по физике – 624
Теплообменник длины $l$ состоит из трубы площадью поперечного сечения $2S$, внутри которой проходит другая труба площадью поперечного сечения $S$ (рис.). Трубы тонкостенные. Вся конструкция теплоизолирована от внешней среды. В трубах со скоростью в прокачивается жидкость плотностью $rho$ и удельной теплоемкостью $c$. Температуры жидкости при входе в теплообменник равны $T_{н2}$ и $T_{н2}$ соответственно.
Определите температуры $T_{к1}$ и $T_{к2}$ жидкости при выходе из теплообменника, если потоки жидкости по трубам текут навстречу друг другу. Считать, что теплота, переданная в единицу времени через единичную площадку, пропорциональна разности температур с коэффициентом пропорциональности $k$. Теплопроводностью жидкости в направлении ее течения пренебречь.
Подробнее
Задача по физике – 627
В холодную погоду изо рта при дыхании идет «пар». Если приоткрыть дверь в теплую избу в морозный день, то в комнату тоже врывается «пар».
Объясните эти явления.
Подробнее
Задача по физике – 628
Сосуд объемом $V = 2 л$ содержит $m_{H_{2}} = 2 г$ водорода и немного воды. Давление в сосуде равно $p_{н} = 17 cdot 10^{5} Па$. Сосуд нагревают так, что давление в нем увеличивается до $p_{к} = 26 cdot 10^{5} Па$, и часть воды испаряется. Молярная масса водяных паров равна $mu =18 cdot 10^{-3} кг/моль$.
Определите начальную $T_{н}$ и конечную $T_{к}$ температуры воды и ее массу $Delta m$.
Указание. Воспользуйтесь следующей температурной зависимостью давления насыщенных паров воды:
| $T,^{circ}C$ | 100 | 120 | 133 | 152 | 180 |
| $p_{нас},10^{5} Па$ | 1 | 2 | 3 | 5 | 10 |
Подробнее
Задача по физике – 629
Нижний конец капилляра радиусом $r = 0,2 мм$ и длины $l = 8 см$ погружен в воду, температура которой постоянна и равна $T_{н} = 0°С$. Температура верхнего конца капилляра равна $T_{в}=100°С;.
На какую высоту $h$ поднимется вода в капилляре? Считать, что теплопроводность капилляра намного превосходит теплопроводность воды в нем. Теплообменом с окружающим воздухом пренебречь.
Указание. Воспользуйтесь следующей температурной зависимостью поверхностного натяжения воды;
| $T,^{circ}C$ | 20 | 50 | 90 | |
| $sigma,мН/м$ | 76 | 73 | 67 | 60 |
Подробнее
Задача по физике – 631
Почему при кладке кирпичных печей используют глиняный раствор для скрепления кирпичей, а не, например, цементный (более прочный)? Учесть, что для кладки печей используют красный кирпич, сделанный из глины.
Подробнее
Задача по физике – 632
В теплоизолированном сосуде имеются две жидкости с начальными температурами $T_{1}$ и $T_{2}$ и удельными теплоемкостями $c_{1}$ и $c_{2}$, разделенные нетеплопроводяшей перегородкой. Перегородку убирают, и после установления теплового равновесия разность между начальной температурой одной из жидкостей и установившейся в сосуде температурой $T$ оказывается в два раза меньше разности начальных температур жидкостей.
Найдите отношение масс жидкостей $m_{1}/m_{2}$.
Подробнее
Задача по физике – 633
В первый раз в пробирку налили воду при температуре $20^{circ}C$. Дно пробирки погрузили в большое количество воды при температуре $80^{circ}C$. Вода в робирке нагрелась за время $t_{1}$ до $80^{circ}C$. Во второй раз в пробирку налили воду при температуре $80^{circ}C$. Дно пробирки погрузили в большое количество воды при температуре $20^{circ}C$. Вода в пробирке охладилась за время $t_{2}$ до $20^{circ}C$.
Какое время больше: $t_{1}$ или $t_{2}$?
Подробнее
Задача по физике – 634
В два одинаковых легких металлических сосуда налили одну и ту же массу воды. Тяжелый шарик (масса которого равна массе воды, а ею плотность много больше плотности воды) опустили на тонкой нетеплопроводяшей нити в один из сосудов так, что он находится в центре объема налитой воды. Сосуды нагрели до температуры кипения воды и поставили остывать. Известно, что время остывания сосуда с шариком до температуры окружающей среды в к раз больше времени остывания сосуда без шарика.
Определите отношение удельных теплоемкостей материала шарика и воды $c_{ш}/c_{в}$.
Подробнее
Задача по физике – 635
Два одинаковых теплоизолированных цилиндрических калориметра высоты $h = 75 см$ заполнены на 1/3. Первый – льдом, образовавшимся в результате замерзания налитой в него воды, второй – водой при $T_{в} = 10^{circ}C$. Воду из второго калориметра переливают в первый, в результате чего он оказывается заполненным на 2/3. После того как температура в первом калориметре установилась, уровень заполнения его увеличился на $Delta h = 0,5 см$. Плотность льда равна $rho_{л} = 0,9 rho_{в}$, удельная теплота плавления льда $lambda = 340 кДж/кг$, удельная теплоемкость льда $c_{л} = 2,1 кДж/(кг cdot К)$, удельная теплоемкость воды $c_{в} = 4,2 кДж/ (кг cdot К)$.
Найти начальную температуру $T_{л}$ льда в первом калориметре.
Подробнее
Задача по физике – 636
Известно, что если обычную воду подсолить, то температура ее кипения станет выше.
Определите, как при этом изменится плотность насыщенных водяных паров при температуре кипения.
Подробнее
Задача по физике – 637
Для многих веществ существует такое значение температуры $T_{тр}$ и давления $p_{тр}$, при котором все три фазы вещества (газообразная, жидкая и твердая) находятся в равновесии друг с другом – так называемая тройная точка вещества. Например, для воды $T_{тр} = + 0,0075^{circ}С, p_{тр} = 4.58 мм рт. ст.$ Удельная теплота испарения воды в тройной точке равна $q = 2,48 cdot 10^{3} кДж/кг$, удельная теплота плавления льда $lambda = 0,34 cdot 10^{3} кДж/кг$.
Найдите удельную теплоту сублимации воды $nu$ (т. е. прямого перехода из твердого в газообразное состояние) в тройной точке.
Подробнее
Источник
D1. Теплоизолированный сосуд разделен на две части легким поршнем. В левой части сосуда находится т1 = 3,0 г водорода при температуре Т1 = =300 К, в правой – т2 = 16 г кислорода при Т2 = 400 К. Поршень слабо проводит тепло, и температура в сосуде постепенно выравнивается. Какое количество теплоты отдаст кислород к тому моменту, когда поршень перестанет двигаться?
D2. В двух одинаковых колбах, соединенных трубкой, перекрытой краном, находится воздух при одинаковых температурах Т1 = Т2 и разных давлениях. После того как кран открыли, часть воздуха перешла из одной колбы в другую. Через некоторое время давления в колбах сравнялись, движение газа прекратилось и температура в одной из колб стала равной Т¢1. Какой будет температура в другой колбе в этот момент? Внутренняя энергия одного моля воздуха U = cT. Объемом соединительной трубки пренебречь. Теплообмен со стенками не учитывать.
D3. В вертикальном цилиндрическом сосуде, площадь сечения которою равна S, под поршнем массы т находится газ, разделенный перегородкой на два одинаковых объема. Давление газа в нижней части сосуда равно р. Внешнее давление равно р0. Температура газа в обеих частях сосуда равна Т. На сколько сместится поршень, если убрать перегородку? Внутренняя энергия одного моля газа U = cT. Высота каждой части сосуда равна h. Стенки сосуда и поршень не проводят тепло. Трением пренебречь.
D4. Поршень удерживается в середине неподвижного теплоизолированного закрытого цилиндрического сосуда длины 2l и площади сечения S. Правую половину сосуда занимает газ, температура и давление которого равны Т1 и р1, в левой половине — вакуум. Поршень соединен с левым торцом сосуда пружиной жесткости к (рис. 19.7). Найти установившуюся температуру газа Т, после того, как поршень отпустили. Длина недеформированной пружины равна 2l. Внутренняя энергия одного моля газа U = cT. Трением, теплоемкостью цилиндра и поршня пренебречь.
D5. В теплоизолированном длинном цилиндрическом сосуде, стоящем вертикально, на высоте h от дна висит на нити поршень массы т. Под поршнем находится один моль газа, давление которого в начальный момент равно атмосферному р0, а температура равна Т0. Какое количество теплоты нужно подвести к газу, чтобы поршень поднялся до высоты 2h? Внутренняя энергия одного моля газа U = cT. Трением пренебречь.
D6. Два цилиндра одинаковой длины l и с площадью сечений: левого, равной S, и правого, равной aS (рис. 19.8), соединены между собой. Посредине каждого цилиндра находятся поршни, соединенные жестким стержнем. Во всех трех отсеках системы находится идеальный газ. Давление в отсеке 1 равно р, а в отсеке 3 – равно βр. Трение пренебрежимо мало, поршни находятся в равновесии. К системе подвели количество теплоты Q так, что температура возросла, оставаясь во всех отсеках одинаковой. Определить изменение давления в отсеке 1. Внутренняя энергия одного моля газа равна U = cT. Теплоемкостью цилиндров и поршней пренебречь.
D7.В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем массы М, находится газ. Газ нагревают. Поршень, двигаясь равноускоренно, приобретает скорость υ. Найти количество теплоты, сообщенной газу. Внутренняя энергия моля газа U = cT. Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь.
D8. В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем, площадь сечения которого равна S, находится один моль газа при температуре Т0 и давлении р0. Внешнее давление постоянно и равно р0 (рис. 19.9). Газ нагревают внешним источником теплоты. Поршень начинает двигаться, причем сила трения скольжения равна f. Найти зависимость температуры газа Т от получаемого им от внешнего источника количества теплоты Q, если в газ поступает еще и половина количества теплоты, выделяющейся при трении поршня о стенки сосуда. Построить график этой зависимости. Внутренняя энергия одного моля газа U = cT. Теплоемкостью сосуда и поршня пренебречь.
Источник
1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)
4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)
7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)
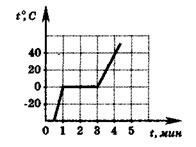8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)
9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)
10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)
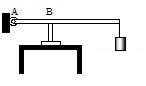11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)
12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)
13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)
14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.
(Решение)
15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)
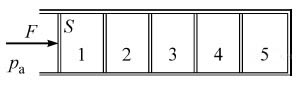16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)
19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)
(Решение)
20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)
21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)
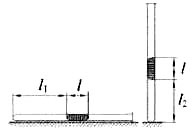22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)
23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)
24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)
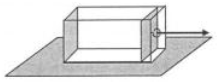25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)
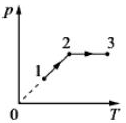26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)
27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)
Источник