Точечный источник света находится в сосуде с жидкостью
32. Электродинамика. Квантовая физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Точечный источник движется со скоростью 2 мм/с вдоль главной оптической оси собирающей линзы с фокусным расстоянием 8 см. С какой скоростью (в мм/с) движется изображение источника в тот момент, когда источник находится от линзы на расстоянии 10 см?
Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}+frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f=frac{Fd}{d-F}] [Gamma=frac{f}{d}=frac{F}{d-F}=frac{8}{2}=4] Возьмем производную по времени [f’=frac{Fd'(d-F)-d’dF}{(d-F)^2}] Заметим, что (v=d’) – скорость предмета, (u=f’) – скорость изображения. [u=frac{Fv(d-F)-vdF}{(d-F)^2}=frac{-F^2v}{(d-F)^2}=-vGamma^2=-2cdot4^2=-32 text{ мм/с}] Знак минус, потому что изображение движется в противоположную сторону.
Ответ: 32
Точечный источник находится на главной оптической оси собирающей линзы с фокусным расстоянием 6 см на расстоянии 8 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в направлении, перпендикулярном оптической оси. С какой скоростью (в мм/с) движется изображение источника?
Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}-frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f=frac{Fd}{F-d}] [Gamma=frac{f}{d}=frac{F}{F-d}=frac{8}{2}=4]
(v) – скорость предмета относительно линзы
(u) – скорость изображения источника [u=vGamma=12 text{ мм/с}]
Ответ: 12
Точечный источник, находящийся на главной оптической оси собирающей линзы на расстоянии от нее, в полтора раза большем фокусного, начинает смещаться со скоростью 4 мм/с перпендикулярно оси. С какой скоростью (в мм/с) движется изображение источника?
Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}+frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f=frac{Fd}{d-F}] [Gamma=frac{f}{d}=frac{F}{d-F}=frac{F}{1,5F-F}=2] [H=hGamma]
(h) – расстояние от предмета до оси
(H) – растояние от изображения до оси
Возьмем производную по времени [u=vGamma=8 text{ мм/с}]
Ответ: 8
Собирающая линза дает изображение некоторого предмета на экране. Высота изображения 9 см. Оставляя неподвижным экран и предмет, линзу передвинули к экрану и получили второе четкое изображение высотой 4 см. Найдите высоту (в см) предмета.
Формула тонкой линзы для собирающей линзы (1): [frac{1}{F}=frac{1}{d_1}+frac{1}{f_1}=frac{d_1+f_1}{d_1f_1}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы
Формула тонкой линзы для собирающей линзы (2): [frac{1}{F}=frac{1}{d_2}+frac{1}{f_2}=frac{d_2+f_2}{d_2f_2}] По условию задачи [d_1+f_1=d_2+f_2] Значит (d_1f_1=d_2f_2) [d_1f_1f_2+f_1^2f_2=d_2f_1f_2+f_2^2f_1] [d_1f_1f_2-d_2f_1f_2=f_2^2f_1-f_1^2f_2] [d_2f_2f_2-d_2f_1f_2=f_2^2f_1-f_1^2f_2] [d_2f_2(f_2-f_1)=f_2f_1(f_2-f_1)] [d_2=f_1,quad d_1=f_2]
Увеличение линзы: [Gamma_1=frac{f_1}{d_1}=frac{d_2}{d_1}=frac{h_1}{H}] [Gamma_2=frac{f_2}{d_2}=frac{d_1}{d_2}=frac{h_2}{H}] [frac{h_1}{H}=frac{H}{h_2}] [H=sqrt{h_1h_2}=6 text{ см}]
Ответ: 6
Точечный источник света находится в ёмкости с жидкостью и опускается вертикально вниз от поверхности жидкости. При этом на поверхности жидкости возникает пятно, в пределах которого лучи света от источника выходят из жидкости в воздух. Глубина погружения источника (расстояние от поверхности жидкости до источника света), измеренная через равные промежутки времени, а также соответствующий радиус светлого пятна представлены в таблице. Чему равен показатель преломления жидкости? (Ответ дайте с точностью до сотых.)
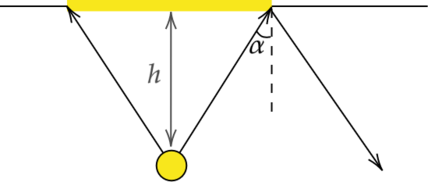
Радиус пятна определяется тем, что не все лучи от источника выходят из воды из-за эффекта полного внутреннего отражения. Рассмотрим предельный случай. [nsinalpha_{text{кр}}=1] [sinalpha_{text{кр}}=frac{R}{sqrt{R^2+h^2}}] [n=frac{sqrt{R^2+h^2}}{R}=frac{sqrt{10^2text{ }+12^2}}{12}=1,30]
Ответ: 1,30
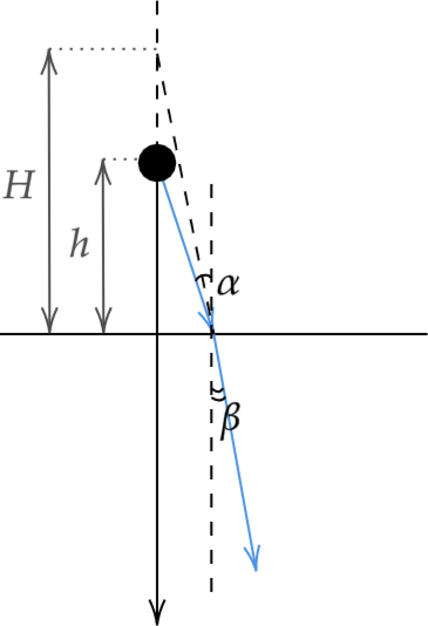
Пловец, нырнувший с открытыми глазами, рассматривает из под воды светящийся предмет, находящийся над его головой на высоте 75 см над поверхностью воды. Какова будет видимая высота (в см) предмета над поверхностью воды? Показатель преломления воды 4/3. Углы считать малыми, т. е. (tgalpha = sinalpha).

Закон преломления [sinalpha=nsinbeta,] где (n) – показатель преломления воды, , (alpha ) – угол падения, (beta) – угол преломления.
Из прямоугольных треугольников: [htgalpha=Htgbeta] [hsinalpha=Hsinbeta] [hnsinbeta=Hsinalpha] [H=hn=75cdot4/3=100 text{ см}]
Ответ: 100
На дне сосуда с водой лежит плоское зеркало. Толщина слоя воды 16 см. На расстоянии 20 см от поверхности воды находится точечный источник света. На каком расстоянии (в см) от зеркала находится его изображение, образуемое лучами, вышедшими обратно из воды? Показатель преломления воды 4/3. Углы считать малыми, т. е. (tgalpha = sinalpha).
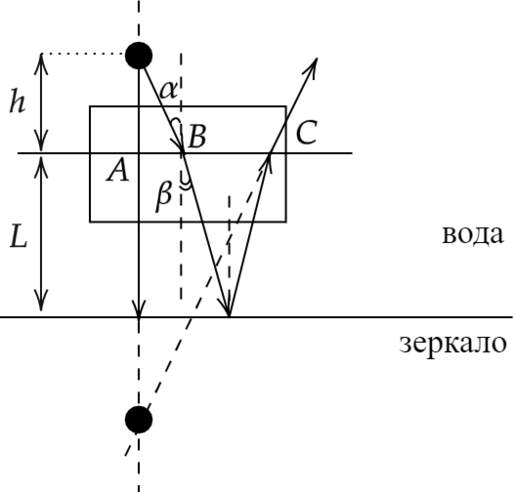
Закон преломления [sinalpha=nsinbeta] где (n) – показатель преломления воды, , (alpha ) – угол падения, (beta) – угол преломления.
Из прямоугольных треугольников: [BC=2Ltgbeta=2Lsinbeta] [AB=htgalpha=hsinalpha] [H+L=frac{AC}{tgalpha}=frac{2Lsinbeta+hsinalpha}{sinalpha}=frac{2L+hn}{n}=frac{2cdot16text{ см}+20text{ см}cdot4/3}{4/3}=44 text{ см}] [H=28 text{ см}]
Ответ: 28
Источник
32. Электродинамика. Квантовая физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
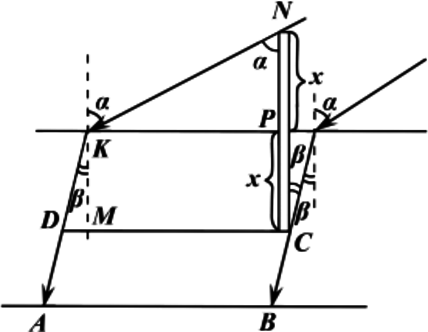
Палка, наполовину погружённая в вертикальном положении в воду, отбрасывает на дно бассейна тень длиной (l = 0, 5) м. Определите длину выступающей над водой части палки, если глубина воды равна (h = 3) м, а угол падения солнечных лучей равен (alpha = 30^circ ) (Показатель преломления воды – 4/3.) Ответ дайте в метрах и округлите до десятых
Построим ход лучей:
Закон преломления:
[sin alpha=n sin beta] (n=4 / 3) (по условию), тогда: [tg=frac{sin beta}{cos beta}=frac{sin beta}{sqrt{1-sin ^{2} beta}}=frac{frac{sin alpha}{n}}{sqrt{1-frac{sin ^{2} alpha}{n^{2}}}}=frac{sin alpha}{sqrt{n^{2}-sin ^{2} alpha}}=frac{1 / 2}{sqrt{(4 / 3)^{2}-(1 / 2)^{2}}}=frac{1 / 2}{sqrt{55 / 36}}=frac{3}{sqrt{55}}] Пусть (x) – длина надводной части палки. Палка погружена наполовину, следовательно, длина подводной части – (x .) Тогда [begin{array}{c}
l=|A B|=|C D|=|P K|+|K M| tg alpha=|P N| tg alpha+x tg beta=x tg alpha+x tg beta \
x=frac{l}{tg alpha+tg beta}=frac{0,5}{frac{3}{sqrt{55}}+frac{1}{sqrt{3}}} approx 0,51 text{ м}
end{array}]
Ответ: 0,5
Бассейн глубиной (H=4) м заполнен водой, относительный показатель преломления на границе воздух-вода (n=4/3). Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?
Пусть (h) – кажущаяся высота.
По закону Снеллиуса [dfrac{sin beta}{sin alpha}= n] Рассмотрим ход лучей

Тогда [h=dfrac{tg alpha}{tg beta} H] Так как углы малые: [happrox dfrac{sin alpha}{sin beta} H approx dfrac{H}{n}=dfrac{4text{ м}}{4/3}approx 3 text{ м}]
Ответ: 3
Бассейн глубиной (H = 3) м заполнен водой, показатель преломления которой (n = 4/3.) Каков радиус светового круга на поверхности воды от электрической лампы на дне бассейна?
Рассмотрим ход лучей
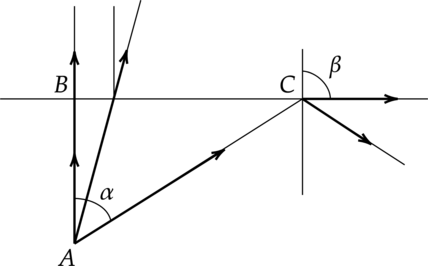
Полное внутреннее отражение происходит начиная с такого значения угла падения (alpha), при котором (beta = 90^circ). По закону преломления [dfrac{sin beta}{sin alpha }= n Rightarrow sin alpha = dfrac{1}{n}] Искомая величина (BC) равна [BC= ABcdot tg alpha =dfrac{AB}{sqrt{n^2-1}}=dfrac{3text{ м}}{sqrt{dfrac{16}{9}-1}}approx 3,4 text{ м}]
Ответ: 3,4
В горизонтальное дно водоема глубиной 3 м вертикально вбита свая, полностью скрытая под водой. При угле падения солнечных лучей на поверхность воды, равном 300, свая отбрасывает на дно водоёма тень длиной 0,8 м. Определите высоту сваи. Показатель преломления воды составляет (n = 4/3.) Ответ дайте в метрах и округлите до целых.
Рассмотрим ход лучей

Длина тени (L) равна (L=hcdot tg beta ), тогда искомая высота сваи (h= dfrac{L}{tg beta}.) По закону преломления [dfrac{sin alpha}{sin beta}=n Rightarrow sin beta = dfrac{sin alpha}{n}] Тангенс угла наклона можно найти как [tg beta = dfrac{sin beta}{cos beta}=dfrac{sin beta}{sqrt{1-sin^2 beta}}=dfrac{1}{4n^2-1}] Тогда искомая высота [h = 0,8text{ м}sqrt{4 cdot dfrac{16}{9}-1}=1,977text{ м}approx 2 text{ м}]
Ответ: 2
В горизонтальное дно водоема глубиной 3 м вертикально вбита свая, полностью скрытая под водой. При угле падения солнечных лучей на поверхность воды, равном 300, свая отбрасывает на дно водоёма тень длиной 0,8 м. Определите высоту сваи. Показатель преломления воды составляет (n = 4/3.) Ответ дайте в метрах и округлите до сотых.
Рассмотрим ход лучей
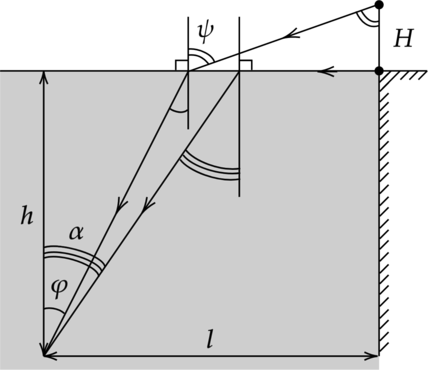
Из закона преломления, луч идущий горизонтально от ног тренера (угол падения равен 90(^circ)) следует по закону полного внутреннего отражения: [sin alpha = dfrac{1}{n} Rightarrow alpha = arcsin dfrac{3}{4}] Аналогично распишем закон преломления для луча идущего от головы тренера: [dfrac{sin psi}{sin varphi}= n Rightarrow sin psi = n sin varphi =dfrac{4}{3}cdot dfrac{1}{2}=dfrac{2}{3}] Из рисунка [H=(l-hcdot tg varphi)ctg psi =(l-h cdot tg varphi) dfrac{cos phi}{sin psi}= (l-h cdot tg varphi)=(l-h cdot tg varphi)dfrac{sqrt{1-sin^2 psi}}{sin psi}=dfrac{sqrt{1-n^2sin^2varphi^2}}{nsin varphi}] Подставляя числа из условий, получим [H= left(3-2,5cdot dfrac{sqrt{3}}{3}right)cdot dfrac{sqrt{5}}{2}approx 1,74text{ м}.]
Ответ: 1,74
Линза, фокусное расстояние которой 15 см, даёт на экране изображение предмета с пятикратным увеличением. Экран пододвинули к линзе вдоль её главной оптической оси на 30 см. Затем при неизменном положении линзы передвинули предмет так, чтобы его изображение на экране снова стало резким. На какое расстояние сдвинули предмет относительно его первоначального положения?
“Основная волна 2020 Вариант 5”
Запишем формулу тонкой Линзы: [dfrac{1}{F}=dfrac{1}{d}+dfrac{1}{f},] где (F) – фокусное расстояние, (d) – расстояние от предмета до линзы, (f) – расстояние от линзы, до изображения.
Откуда фокусное расстояние: [F=dfrac{fd}{f+d}] Увеличение линзы же составит [text{Г}=dfrac{f}{d}] Первоначальное увеличение составляет 5, значит (f=5d), откуда из фокусного расстояния [F=dfrac{5d^2}{6d}=dfrac{5}{6}d Rightarrow d= 1,2F=18text{ см}] (f=18cdot 5 =90text{ см}). После того как экран и предмет передвинули, для нового положения предмета и изображения можно записать [F=dfrac{f_1d_1}{f_1+d_1}] Опять же (f_1=f-30=60), откуда (d_1) [dfrac{1}{d_1}=dfrac{1}{F}-dfrac{1}{f_1} Rightarrow dfrac{1}{d_1}=dfrac{f_1-F}{Ff_1} Rightarrow] [d_1=dfrac{Ff_1}{f_1-F}=dfrac{15text{ см}cdot 60text{ см}}{60text{ см}-15text{ см}}=20text{ см}] Откуда разность [Delta d= d_1-d=2text{ см}]
Ответ: 2
Точечный источник света находится на расстоянии 12 см от собирающей линзы с фокусным расстоянием 10 см. За линзой на расстоянии 10 см установлено плоское зеркало, перпендикулярное главной оптической оси линзы. На каком расстоянии (в см) от линзы находится изображение, образованное лучами, прошедшими через линзу после отражения от зеркала?
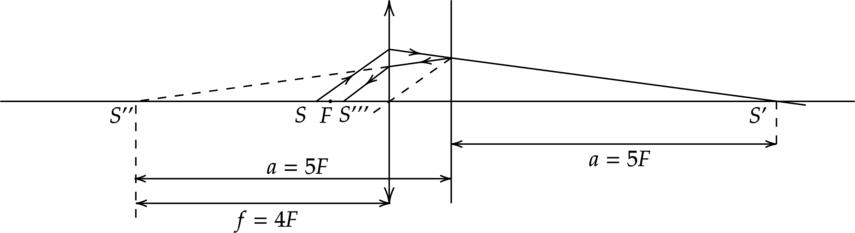
Формула тонкой линзы для собирающей линзы(без участия зеркала): [frac{1}{F}=frac{1}{d_1}+frac{1}{f_1}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f_1=frac{Fd_1}{d_1-F}=frac{10cdot12}{12-10}=60 text{ см}] Отразим лучи в зеркале после прохождения линзы один раз, получаем (S”) – мнимый предмет, расстояние (d_2=40) см
Формула тонкой линзы для собирающей линзы (предмет S”, изображение S”’): [frac{1}{F}=-frac{1}{d_2}+frac{1}{f_2}] [f_2=frac{Fd_2}{F+d_2}=frac{10text{ см}cdot40text{ см}}{50text{ см}}=8 text{ см}]
Ответ: 8
Источник
