Три сосуда с одинаковыми объемами сообщаются между собой кранами

1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд — со вторым, второй — с третьим. Первоначально давление газа в сосудах было равно соответственно (р, 3р) и (р). В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
1) При первой открывании и закрывании кранов, в соответствии законам Дальтона и Бойля-Мариотта, установившееся давление во втором и третьем сосудах будет [dfrac{3p}{2}+dfrac{p}{2}=2p] 2) При втором открывании и закрывании, с учетом тех же законов, установившееся давление в первом и втором будет равно [dfrac{2p}{2}+dfrac{p}{2}=1,5p] 3) Так как объем сосуда не изменился, а температура по условию постоянна, то в соответствии закону Клайперона – Менделеева [pV=nu R T Rightarrow nu=dfrac{pV}{RT}] Знаменатель остался прежним, а числитель увеличился, значит и количество газа увеличилось.
Ответ:
Сжиженные газы с низкими температурами кипения хранят в открытых теплоизолированных резервуарах при нормальном давлении, с контактом с атмосферой. При таком хранении потери на испарение, отнесённые к единице массы сжиженного газа, уменьшаются при увеличении объёма сосуда. Объясните причины вышеизложенного, основываясь на известных физических законах и закономерностях.
1) Даже при хорошей теплоизоляции невозможно устранить полностью подвод тепла к сжиженным газам, значит, будет некоторое испарение вещества, потому что температура кипения таких газов ниже температуры атмосферы и существует теплопроводность.
2) Так как существует испарение, то в закрытых сосудах будет повышаться давление, что приведет к взрыву, поэтому газ хранят в открытых сосудах.
3) Подвод тепла к газу через стенки сосуда пропорционален площади стенок сосуда, а его масса пропорциональна объему. Объем же в свою очередь пропорционален кубу размеров сосуда. Поэтому с увеличением объема уменьшается испарение на единицу массы.
Ответ:
Чтобы вода в резервуаре быстрее закипела, источник тепла всегда помещают внизу. Желая охладить кастрюлю с горячей водой как можно быстрее, кастрюлю поставили на лёд. Является ли такой способ эффективным? Ответ поясните, указав какие физические явления и закономерности вы использовали для объяснения.
Нет, неверно.
Нагреватель ставится внизу, потому что нагретые слои воды, как более легкие, поднимаются вверх и таким образом достигается наиболее эффективное перемешивание и нагревание всей воды (по такому же принципу работает батарея в комнате). При охлаждении же дело происходит как раз наоборот: более холодные слои воды, как более тяжелые, опускаются вниз. Поэтому если поместить холодильник внизу, то перемешивания не будет, и остывание будет идти очень долго. Для более быстрого охлаждения надо поместить лед сверху.
Ответ:
На рисунке изображены графики двух процессов, проведённых с идеальным газом при одном и том же давлении. Графики процессов представлены на рисунке. Почему изобара (I) лежит выше изобары (II)? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения. 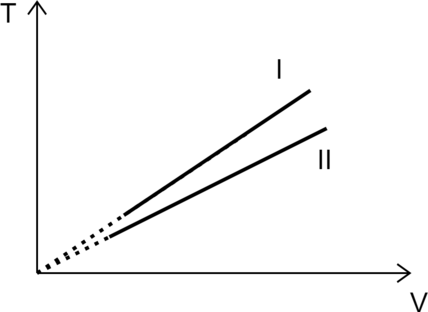
1. Идеальный газ подчиняется закону Клапейрона–Менделеева: [pV=nu R T,] где (p) – давление газа, (V) – объем, (nu) – количество газа, (T) – температура газа в Кельвинах.
Выразим температуру [T=dfrac{pV}{nu R}] 2. Зафиксируем объем (V_0), при этом отношение температур равно [dfrac{T_I}{T_{II}}=dfrac{dfrac{pV_0}{nu_I R}}{dfrac{pV_0}{nu{II}R}}=dfrac{nu_{II}}{nu_{I}}>1] Значит количество газа во втором больше, чем количество газа в первом.
Ответ:
1 моль разреженного гелия участвует в циклическом процессе 1–2–3–4–1, график которого изображён на рисунке в координатах V–T, где V — объём газа, Т — абсолютная температура. Постройте график цикла в координатах p–V, где р — давление газа, V— объём газа. Опираясь на законы молекулярной физики и термодинамики, объясните построение графика. Определите, во сколько раз работа газа в процессе 2–3 больше модуля работы внешних сил в процессе 4–1. 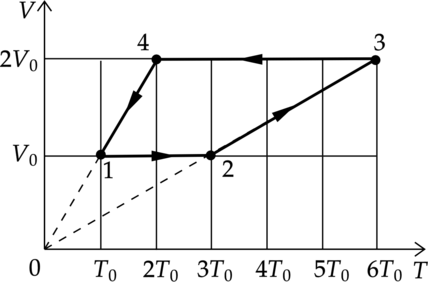
Проанализируем процессы:
1–2: Процесс изохорный, по закону Шарля (dfrac{p}{T}=const), температура увеличилась в 3 раза, значит и давление увеличилось в 3 раза.
2–3: Процесс изобарный, по закону Гей–Люсака (dfrac{V}{T}=const) и объем и температура увеличились в 2 раза.
3–4: В процессе 3–4 газ изохорно уменьшил свою абсолютную температуру и давление в 3 раза.
4–1: Газ вернулся в первоначальное состояние Перестроим график цикла в координатах p–V (см. рисунок). 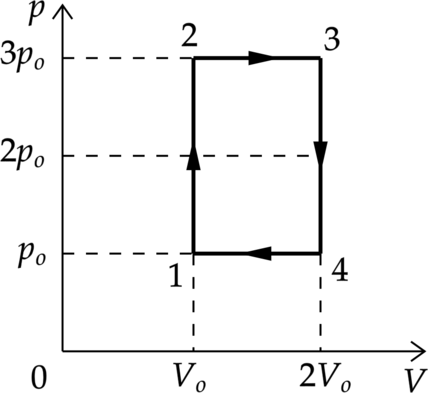
Работа газа в процессе 2–3 равна [A_{23}=pDelta V=3p_(2V_0-V_0)=3p_0V_0] Работа внешних сил в процессе 4–1 равна [|A_{41}|=pDelta V=p_0(2V_0-V_0)=p_0V_0] Значит работа газа в процессе 2–3 в 3 раза больше работы внешних сил в процессе 4–1.
Ответ:
На рисунке 1 приведена зависимость внутренней энергии (U) 2 моль идеального одноатомного газа от его давления p в процессе 1–2–3. Постройте график этого процесса на рисунке 2 в переменных (p—V). Точка, соответствующая состоянию 1, уже отмечена на этом рисунке. Построение объясните, опираясь на законы молекулярной физики. 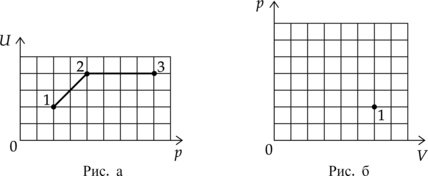
1. Проанализируем процессы:
1–2: Внутренняя энергия прямо пропорциональна температуре газа (U=dfrac{3}{2}nu R T ), значит в процессе 1–2 температура увеличивается, давление тоже увеличивается (по графику ). По основному газовому закону (dfrac{pV}{T}=const) объем будет постоянен. График будет представлять собой вертикальную прямую
2–3: В процессе 2–3 внутренняя энергия газа постоянна, а значит и температура постоянна (по пункту 1), давление увеличивается, значит, по основному газовому закону объем будет уменьшаться. График будет представлять гиперболу.
2. Построим график

Ответ:
На графике представлена зависимость давления неизменной массы идеального газа от его плотности. Опишите, как изменяются в зависимости от плотности температура и объём газа в процессах 1–2 и 2–3. 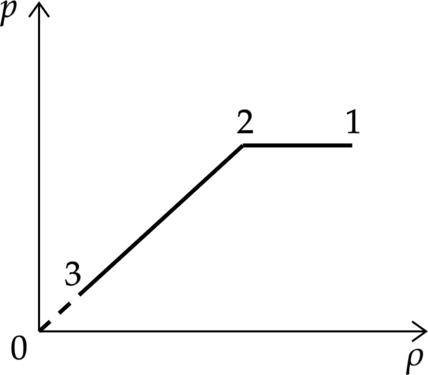
1. Плотность находится по формуле: [rho=dfrac{m}{V} quad (1)] тогда уравнение Клайперона–Менделеева можно переписать в виде [pV=dfrac{m}{mu}RT Rightarrow p=dfrac{rho}{mu}RT, quad (2)] где (m) – масса газа, (V) – его объем, (T) – температура газа. 2. Процесс 1–2.
Плотность уменьшается при постоянном, в соответствии с формулой (1) объем будет увеличиваться, а температура будет увеличиваться в соответствии с формулой (2).
Процесс 2–3.
Плотность уменьшается вместе с давлением, причем давление уменьшается пропорционально плотности (p sim rho), а это означает, что температура газа постоянна, а по формуле (1) объем увеличивается.
Ответ:
Источник
Pages: | 1 | … | 2 | 3 |
| 5 | 6 | … | 28 |
— [ Ñòðàíèöà 4 ] —
2.14. Òðè ñîñóäà ñ îäèíàêîâûìè îáúåìàìè ñîîáùàþòñÿ ìåæäó ñîáîé òðóáêàìè, ïåðåêðûòûìè êðàíàìè. Ïåðâûé ñîñóä ñîäåðæèò ìîëåé íåêîòîðîãî ãàçà, òðåòèé 2 ìîëåé òîãî æå ãàçà, âî âòîðîì ñîñóäå íàõîäèòñÿ âàêóóì. Ñíà÷àëà ñîåäèíèëè âòîðîé è òðåòèé ñîñóäû, à ïîñëå óñòàíîâëåíèÿ ðàâíîâåñèÿ âòîðîé ñîñóä îòñîåäèíèëè îò òðåòüåãî è ñîåäèíèëè ñ ïåðâûì.  ðåçóëüòàòå äàâëåíèå â ïåðâîì è âòîðîì ñîñóäàõ óñòàíîâèëîñü ðàâíûì p. Íàéòè íà÷àëüíîå äàâëåíèå â ïåðâîì ñîñóäå. Òåìïåðàòóðà ïîñòîÿííà.
2.15. Âíóòðè çàêðûòîãî ñ îáîèõ êîíöîâ ãîðèçîíòàëüíîãî öèëèíäðà èìååòñÿ òîíêèé ïîðøåíü, êîòîðûé ìîæåò ñêîëüçèòü â öèëèíäðå áåç òðåíèÿ. Ñ îäíîé ñòîðîíû ïîðøíÿ íàõîäèòñÿ âîäîðîä ìàññîé m1 = 3 ã, ñ äðóãîé àçîò ìàññîé m2 = 21 ã. Êàêóþ ÷àñòü îáúåìà öèëèíäðà çàíèìàåò âîäîðîä? Òåìïåðàòóðà ãàçîâ îäèíàêîâà.
2.16 (ÂÝ, 2006). Öèëèíäðè÷åñêèé ñîñóä äåëèòñÿ íà äâå ÷àñòè òîíêèì ïîäâèæíûì ïîðøíåì.  îäíó ÷àñòü ñîñóäà ïîìåùàþò íåêîòîðîå êîëè÷åñòâî ãåëèÿ, â äðóãóþ òàêîå æå (ïî ìàññå) êîëè÷åñòâî àçîòà ïðè îäèíàêîâûõ òåìïåðàòóðàõ, è ïîðøåíü ïðèõîäèò â ñîñòîÿíèå ðàâíîâåñèÿ. Íàéòè äëèíó òîé ÷àñòè ñîñóäà, â êîòîðîé íàõîäèòñÿ ãåëèé. Äëèíà ñîñóäà l = 32 ñì.
2.17 (ÂÝ, 2003). Âîçäóõ âíóòðè îòêðûòîé â àòìîñôåðó îáîëî÷êè âîçäóøíîãî øàðà îáúåìîì V íàãðåâàþò ãàçîâîé ãîðåëêîé äî òåìïåðàòóðû T, ïðåâûøàþùåé òåìïåðàòóðó îêðóæàþùåãî âîçäóõà T0. Êàêóþ ìàññó ìîæåò ïîäíÿòü âîçäóøíûé øàð? Ìàññîé îáîëî÷êè øàðà ïðåíåáðå÷ü. Àòìîñôåðíîå äàâëåíèå p0, ìîëÿðíàÿ ìàññà âîçäóõà .
2.18. Ìàññà m = 716 ìã îðãàíè÷åñêîãî ñîåäèíåíèÿ, èìåþùåãî ôîðìóëó (C3H6O)n, íàõîäèòñÿ â ãàçîîáðàçíîì ñîñòîÿíèè â ñîñóäå îáúåìîì V = 243 ñì3. Ïðè òåìïåðàòóðå t = 200 °Ñ ãàç îêàçûâàåò äàâëåíèå p = 105 Ïà. Íàéòè çíà÷åíèå n. Àòîìíûå ìàññû âîäîðîäà, óãëåðîäà è êèñëîðîäà, ñîîòâåòñòâåííî, ðàâíû: H = 1 ã/ìîëü, C = = 12 ã/ìîëü, O = 16 ã/ìîëü. Ñ÷èòàòü, ÷òî ãàç èäåàëüíûé.
2.19 (ÂÝ, 2003 2006). Íàéòè ôîðìóëó ãàçîîáðàçíîãî ñîåäèíåíèÿ óãëåðîäà ñ êèñëîðîäîì, åñëè èçâåñòíî, ÷òî ìàññà m = 1 ã ýòîãî ñîåäèíåíèÿ, ïîìåùåííàÿ â îáúåì V = 1 äì3 ïðè òåìïåðàòóðå t = 27 °Ñ, îêàçûâàåò äàâëåíèå p = 5,6 104 Ïà.
2.20 (ÂÝ, 2006 2007).  âåðòèêàëüíîì öèëèíäðè÷åñêîì ñîñóäå ïëîùàäüþ ñå÷åíèÿ S ïîä íåâåñîìûì ïîðøíåì íàõîäèòñÿ âîçäóõ è ðåçèíîâûé øàðèê îáúåìîì V ñ äàâëåíèåì âîçäóõà â íåì p (p p0).
Íà ñêîëüêî ïîäíèìåòñÿ èëè îïóñòèòñÿ ïîðøåíü, åñëè øàðèê ëîïíåò? Òðåíèÿ íåò, àòìîñôåðíîå äàâëåíèå p0, òåìïåðàòóðà âîçäóõà â ñîñóäå íåèçìåííà.
2.21 (ÂÝ, 2005, 2007). Äëÿ èçìåðåíèÿ ñîáñòâåííîãî îáúåìà ñûïó÷åãî ìàòåðèàëà åãî ïîìåùàþò â öèëèíäð, êîòîðûé ãåðìåòè÷åñêè çàêðûâàþò ïîðøíåì. Çàòåì èçìåðÿþò äàâëåíèå âîçäóõà âíóòðè öèëèíäðà p1 è p2 (p2 p1) ïðè îäíîé è òîé æå òåìïåðàòóðå è äâóõ ïîëîæåíèÿõ ïîðøíÿ, êîãäà ñóììàðíûå îáúåìû âîçäóõà è ìàòåðèàëà ðàâíû V1 è V2. Íàéòè ïî ýòèì äàííûì îáúåì ìàòåðèàëà.
2.22 (Î, 2007). Â íåêîòîðîì òåïëîâîì ïðîöåññå îáúåì èäåàëüíîãî ãàçà çàâèñèò îò åãî òåìïåðàòóðû ïî çàêîíó V = T2. Âî ñêîëüêî ðàç èçìåíÿåòñÿ äàâëåíèå ãàçà â ýòîì ïðîöåññå ïðè èçìåíåíèè åãî îáúåìà îò V1 äî V2?
2.23 (Î, 2007). Â íåêîòîðîì òåïëîâîì ïðîöåññå äàâëåíèå èäåàëüíîãî ãàçà çàâèñèò îò òåìïåðàòóðû ïî çàêîíó P = T2. Âî ñêîëüêî ðàç èçìåíÿåòñÿ äàâëåíèå ãàçà ïðè èçìåíåíèè åãî îáúåìà îò V1 äî V2?
2.24 (ÂÝ, 2006 2007). Öèëèíäð ðàçäåëåí íà äâà ðàâíûõ îòñåêà ïåðåãîðîäêîé ñ îòâåðñòèåì, çàêðûòûì ïðîáêîé. Â îáîèõ îòñåêàõ ñîäåðæèòñÿ îäèíàêîâûé ãàç ïîä äàâëåíèåì p. Ïðîáêà âûëåòàåò, êîãäà ïåðåïàä äàâëåíèé â îòñåêàõ ðàâåí p. Ñ îäíîãî êîíöà öèëèíäð çàïàÿí, ñ äðóãîãî çàêðûò ïîðøíåì. Ïîðøåíü ìåäëåííî âûòÿãèâàþò, ïîêà ïðîáêà íå âûëåòèò, â ýòîò ìîìåíò âûòÿãèâàíèå ïðåêðàùàþò. Íàéòè óñòàíîâèâøååñÿ äàâëåíèå. Òåìïåðàòóðà ïîñòîÿííà.
2.25. Öèëèíäð ðàçäåëåí íà äâà ðàâíûõ îòñåêà ïåðåãîðîäêîé ñ îòâåðñòèåì, çàêðûòûì ïðîáêîé. Â îáîèõ îòñåêàõ ñîäåðæèòñÿ îäèíàêîâûé ãàç ïîä äàâëåíèåì p. Ïðîáêà âûëåòàåò, êîãäà ïåðåïàä äàâëåíèé â îòñåêàõ ðàâåí p. Ãàç â îäíîì îòñåêå íàãðåâàþò äî òåõ ïîð, ïîêà ïðîáêà íå âûëåòèò, â ýòîò ìîìåíò íàãðåâàíèå ïðåêðàùàþò. Íàéòè äàâëåíèå ãàçà ïîñëå óñòàíîâëåíèÿ ðàâíîâåñèÿ.
2.26 (Î, 2004).  âåðòèêàëüíîì öèëèíäðè÷åñêîì ñîñóäå ïîä ìàññèâíûì ïîðøíåì íàõîäèòñÿ èäåàëüíûé ãàç. ×òîáû óìåíüøèòü îáúåì ãàçà â n = 2 ðàçà, íà ïîðøåíü íàäî ïîëîæèòü ãðóç ìàññîé m = 1 êã. Êàêîé åùå ãðóç íàäî ïîëîæèòü íà ïîðøåíü, ÷òîáû óìåíüøèòü îáúåì ãàçà åùå â k = 3 ðàçà? Òåìïåðàòóðà ïîääåðæèâàåòñÿ ïîñòîÿííîé.
(S2 S1) ñîñòûêîâàíû ìåæäó ñîáîé. Â íèõ âñòàâëåíû ñîåäèíåííûå ñòåðæíåì ïîðøíè, êîòîðûå îäèíàêîâûõ ðàññòîÿíèÿõ îò ñòûêà òðóá. Ìåæäó ïîðøíÿìè íàõîäèòñÿ èäåàëüíûé ãàç. Ïðè êàêîé òåìïåðàòóðå ãàçà ìåæäó ïîðøíÿìè ëåâûé ïîðøåíü ñìåñòèòñÿ âïðàâî äî ñòûêà òðóá? À ïðè êàêîé òåìïåðàòóðå äî ñòûêà òðóá ïåðåìåñòèòñÿ ïðàâûé ïîðøåíü?
îäíîìó ìîëþ èäåàëüíîãî ãàçà. Ê ïîðøíþ ïðèëîæèëè ãîðèçîíòàëüíóþ ñèëó F. Êàêèì áóäåò ïîëîæåíèå ïîðøíÿ ïðè óñòàíîâèâøåìñÿ äâèæåíèè? Äëèíà ñîñóäà l. Òåìïåðàòóðà ãàçà ïîñòîÿííà è ðàâíà T.
Ìàññà ñîñóäà ðàâíà ìàññå ïîðøíÿ. Ìàññà ãàçà ìíîãî ìåíüøå ìàññ ñîñóäà è ïîðøíÿ.
2.29.  çàêðûòîé, ÷àñòè÷íî îòêà÷åííîé òðóáêå íàõîäèòñÿ ñòîëáèê ðòóòè äëèíîé l. Åñëè òðóáêà ðàñïîëîæåíà ãîðèçîíòàëüíî, òî ñòîëáèê íàõîäèòñÿ ïîñåðåäèíå. Åñëè òðóáêó ïîñòàâèòü âåðòèêàëüíî, âåðõíèé îáúåì áóäåò âäâîå áîëüøå íèæíåãî. Íàéòè äàâëåíèå âîçäóõà â ãîðèçîíòàëüíî ðàñïîëîæåííîé òðóáêå. Ïëîòíîñòü ðòóòè ñ÷èòàòü èçâåñòíîé. Òåìïåðàòóðà íå èçìåíÿåòñÿ.
2.30. Îòêðûòóþ âåðòèêàëüíóþ òðóáêó äëèíîé l îïóñêàþò â æèäêîñòü ñ ïëîòíîñòüþ íà ãëóáèíó l/2, çàòåì çàòûêàþò âåðõíåå îòâåðñòèå è âûòàñêèâàþò òðóáêó èç æèäêîñòè. Èçâåñòíî, ÷òî â òðóáêå îñòàåòñÿ ñòîëáèê æèäêîñòè âûñîòîé x. Íàéòè àòìîñôåðíîå äàâëåíèå. Òåìïåðàòóðà íå èçìåíÿåòñÿ.
2.31. Âåðòèêàëüíóþ öèëèíäðè÷åñêóþ òðóáêó äëèíîé l, çàïàÿííóþ ñ îäíîãî êîíöà (ðèñóíîê à), ïîëíîñòüþ ïîãðóæàþò îòêðûòûì êîíöîì â æèäêîñòü ïëîòíîñòüþ (ðèñóíîê á). Íàéòè êå. Àòìîñôåðíîå äàâëåíèå pa.
Òåìïåðàòóðà íå èçìåíÿåòñÿ.
2.32 (Î, 2003). Âåðòèêàëüíî ðàñïîëîæåííûé çàïàÿííûé öèëèíäðè÷åñêèé ñîñóä ðàçäåëåí íà äâå ÷àñòè ïîäâèæíûì ïîðøíåì. Íàä è ïîä ïîðøíåì íàõîäÿòñÿ îäèíàêîâûå êîëè÷åñòâà îäèíàêîâîãî èäåàëüíîãî ãàçà, ïðè ýòîì îáúåì íèæíåé ÷àñòè ñîñóäà âäâîå ìåíüøå îáúåìà âåðõíåé. Òåìïåðàòóðà ãàçîâ îäèíàêîâà è ðàâíà T1. Êàêèì áóäåò ñîîòíîøåíèå îáúåìîâ âåðõíåé è íèæíåé ÷àñòåé ñîñóäà ïðè óâåëè÷åíèè òåìïåðàòóðû ãàçîâ äî T2? Òðåíèå ìåæäó ïîðøíåì è ñòåíêàìè ñîñóäà îòñóòñòâóåò.
2.33. Ðòóòíûé áàðîìåòð äàåò íåïðàâèëüíûå ïîêàçàíèÿ èç-çà âîçäóõà íàä ðòóòüþ â òðóáêå. Ïðè èñòèííîì äàâëåíèè p1 îí ïîêàçûâàåò p1 (ò.å. âûñîòà ñòîëáèêà ðòóòè ðàâíà p1 / g, ïëîòíîñòü ðòóòè). ×åìó ðàâíî èñòèííîå äàâëåíèå p2 ïðè ïîêàçàíèè áàðîìåòðà p 2, åñëè ðàññòîÿíèå îò óðîâíÿ ðòóòè äî âåðõíåãî êîíöà òðóáêè ðàâíî l? Òåìïåðàòóðà ïîñòîÿííà.
2.34 (Î, 2006).  ãîðèçîíòàëüíîì öèëèíäðè÷åñêîì ñîñóäå äëèíîé l íàõîäÿòñÿ n ïîäâèæíûõ òåïëîíåïðîíèöàåìûõ ïîðøíåé, äåëÿùèõ ñîñóä íà n + 1 îòñåê (ñì. ðèñóíîê). Ïåðâîíà÷àëüíî òåìïåðàòóðà ãàçà âî âñåõ îòñåêàõ áûëà ðàâíà T0, îáúåìû âñåõ îòñåêîâ îäèíàêîâû. Çàòåì ãàç â ñàìîì ëåâîì îòñåêå íàãðåâàþò äî òåìïåðàòóðû T1, à òåìïåðàòóðó ãàçà â äðóãèõ îòñåêàõ ïîääåðæèâàþò ðàâíîé T0. Íà ñêîëüêî ñìåñòèòñÿ ïðè ýòîì ñàìûé ïðàâûé ïîðøåíü?
ÃÐÀÔÈ×ÅÑÊÈÅ ÇÀÄÀ×È ÍÀ ÃÀÇÎÂÛÅ ÇÀÊÎÍÛ
Ïðåäñòàâëåíèå òåïëîâûõ ïðîöåññîâ ñ ïîìîùüþ ãðàôèêîâ çàâèñèìîñòè îäíîãî ìàêðîñêîïè÷åñêîãî ïàðàìåòðà ãàçà îò äðóãîãî ÿâëÿåòñÿ î÷åíü óäîáíûì è ïëîäîòâîðíûì, ïîñêîëüêó ïîçâîëÿåò «óâèäåòü» âåñü ïðîöåññ â öåëîì è ïîìîãàåò âûäåëèòü íàèáîëåå õàðàêòåðíûå åãî ÷åðòû.
Äëÿ ïîñòðîåíèÿ ãðàôèêîâ òåõ èëè èíûõ ïðîöåññîâ, ïðîèñõîäÿùèõ ñ èäåàëüíûì ãàçîì, èñïîëüçóþòñÿ òàêèå ñîîáðàæåíèÿ. Âîïåðâûõ, ïðîöåññ äîëæåí áûòü êàê-òî çàäàí óñëîâèåì çàäà÷è, íàïðèìåð çàäàíà çàâèñèìîñòü äàâëåíèÿ ãàçà îò åãî îáúåìà â ýòîì ïðîöåññå. Çà èçìåíåíèåì äðóãèõ æå ïàðàìåòðîâ ãàçà ìîæíî ïðîñëåäèòü ñ ïîìîùüþ óðàâíåíèÿ ñîñòîÿíèÿ (óðàâíåíèÿ Êëàïåéðîíà Ìåíäåëååâà), êîòîðîå ñâÿçûâàåò âñå ìàêðîñêîïè÷åñêèå ïàðàìåòðû ãàçà. Ðàññìîòðèì ïðèìåð.
Ïðèìåð 3.1. Ïîñòðîèòü ãðàôèêè èçîòåðìè÷åñêîãî, èçîõîðè÷åñêîãî è èçîáàðè÷åñêîãî ïðîöåññîâ â êîîðäèíàòíûõ îñÿõ p T, V T è p V. Êàê áóäóò èçìåíÿòüñÿ ãðàôèêè ïðè èçìåíåíèè òåìïåðàòóðû, îáúåìà è äàâëåíèÿ?
Ðåøåíèå.  èçîòåðìè÷åñêîì ïðîöåññå íå èçìåíÿåòñÿ òåìïåðàòóðà ãàçà: T = const, íî èçìåíÿþòñÿ åãî äàâëåíèå è îáúåì.
Ïîýòîìó ãðàôèêàìè ýòîãî ïðîöåññà èçîòåðìàìè íà êîîðäèíàòíûõ ïëîñêîñòÿõ p T è V T áóäóò âåðòèêàëüíûå ïðÿìûå. Ïðè ýòîì âîçìîæíû äâà íàïðàâëåíèÿ èçîòåðìè÷åñêîãî ïðîöåññà ñ óâåëè÷åíèåì èëè óìåíüøåíèåì îáúåìà. Êàê ñëåäóåò èç çàêîíà Êëàïåéðîíà Ìåíäåëååâà, äàâëåíèå ãàçà áóäåò, ñîîòâåòñòâåííî, óìåíüøàòüñÿ èëè óâåëè÷èâàòüñÿ â ýòèõ ïðîöåññàõ. Íà ðèñ. 1, à, á â êîîðäèíàòíûõ îñÿõ p T è V T ñïëîøíîé ëèíèåé ïðåäñòàâëåíû ãðàôèêè èçîòåðìè÷åñêîãî ïðîöåññà, â êîòîðîì ðàñòåò äàâëåíèå ãàçà è óáûâàåò îáúåì (ýòî ïîêàçàíî ñòðåëêàìè íà ãðàôèêàõ). Åñëè íàãðåòü ãàç, à çàòåì ïðîâåñòè ñ íèì èçîòåðìè÷åñêèé ïðîöåññ ïðè áîëüøåé òåìïåðàòóðå, òî ñîîòâåòñòâóþùèå èçîòåðìû áóäóò ðàñïîëîæåíû íà ãðàôèêàõ p T è V T ïðàâåå. Íà ðèñ. 1, à, á ýòè èçîòåðìû ïîêàçàíû ïóíêòèðîì. Îòìåòèì, ÷òî èçîòåðìà íà ïëîñêîñòè V T íå ìîæåò äîõîäèòü äî îñè T, ïîñêîëüêó ýòî îòâå÷àëî áû íóëåâîìó îáúåìó ãàçà. Íà ãðàôèêå p T èçîòåðìà ôîðìàëüíî äîõîäèòü äî îñè òåìïåðàòóð ìîæåò, íî ýòî îòâå÷àëî áû áåñêîíå÷íî áîëüøîìó îáúåìó ãàçà.
×òîáû ïîñòðîèòü èçîòåðìó íà ãðàôèêå p V, çàìåòèì, ÷òî èç çàêîíà (*) ñëåäóåò, ÷òî â èçîòåðìè÷åñêîì ïðîöåññå äàâëåíèå çàâèñèò îò îáúåìà ïî çàêîíó ãäå âåëè÷èíà = RT = const ÿâëÿåòñÿ ïîñòîÿííîé. Çàâèñèìîñòü (**) íà ãðàôèêå p V èçîáðàæàåòñÿ ãèïåðáîëîé. Äëÿ èçîòåðì, îòâå÷àþùèõ áîëüøåé òåìïåðàòóðå, âåëè÷èíà áîëüøå, è, ñëåäîâàòåëüíî, ñîîòâåòñòâóþùèå ãèïåðáîëû áóäóò ðàñïîëîæåíû âûøå. Íà ðèñ. 1, â íà êîîðäèíàòíîé ïëîñêîñòè p V ñïëîøíîé ëèíèåé ïîêàçàí ãðàôèê èçîòåðìè÷åñêîãî ïðîöåññà. Ñòðåëêà íà èçîòåðìå ïîêàçûâàåò íàïðàâëåíèå ïðîöåññà (âîçðàñòàíèå äàâëåíèÿ è óáûâàíèå îáúåìà). Ïóíêòèðîì ïîêàçàíû èçîòåðìû, îòâå÷àþùèå áîëüøåé òåìïåðàòóðå.
 èçîõîðè÷åñêîì ïðîöåññå íå ìåíÿåòñÿ îáúåì ãàçà (V = const), ïîýòîìó ãðàôèêàìè ýòîãî ïðîöåññà èçîõîðàìè íà êîîðäèíàòíûõ ïëîñêîñòÿõ V T è p V áóäóò, ñîîòâåòñòâåííî, ãîðèçîíòàëüíûå è âåðòèêàëüíûå ïðÿìûå. Ïðè ýòîì èç çàêîíà (*) ñëåäóåò, ÷òî äàâëåíèå è òåìïåðàòóðà â èçîõîðè÷åñêîì ïðîöåññå ëèáî îäíîâðåìåííî ðàñòóò, ëèáî îäíîâðåìåííî óáûâàþò. Èçîõîðû íà êîîðäèíàòíûõ ïëîñêîñòÿõ V T è p V ïîêàçàíû íà ðèñ. 2, á, â (ïóíêòèðîì èçîõîðû, îòâå÷àþùèå áîëüøåìó îáúåìó).
Èçîõîðà íà ãðàôèêå p T ñòðîèòñÿ ñëåäóþùèì îáðàçîì.
Êàê ñëåäóåò èç çàêîíà (*), â èçîõîðè÷åñêîì ïðîöåññå äàâëåíèå çàâèñèò îò òåìïåðàòóðû ïî çàêîíó ãäå = R/V = const â èçîõîðè÷åñêîì ïðîöåññå. Çàâèñèìîñòè (***) îòâå÷àåò ïðÿìàÿ, ïðè÷åì ïðîõîäÿùàÿ ÷åðåç íà÷àëî êîîðäèíàò. Îäíàêî ïðè ïîñòðîåíèè òàêîé ïðÿìîé «äîâîäèòü»
åå äî íà÷àëà êîîðäèíàò íåëüçÿ. Ýòî ñâÿçàíî ñ òåì, ÷òî ïðè ìàëûõ òåìïåðàòóðàõ ãàç ïåðåñòàíåò áûòü ãàçîì, è âñå çàâèñèìîñòè èçìåíÿòñÿ. Ïîýòîìó îáû÷íî ïðè ïîñòðîåíèè èçîõîðû íà ãðàôèêå p T åå «íèæíèé êóñî÷åê» èçîáðàæàþò ïóíêòèðîì, ÷òîáû ïîêàçàòü, ÷òî èçîõîðå îòâå÷àåò ïðÿìàÿ, ïðîäîëæåíèå êîòîðîé ïðîõîäèò ÷åðåç íà÷àëî êîîðäèíàò (ðèñ. 2, à).
Äëÿ ïîñòðîåíèÿ èçîõîð, îòâå÷àþùèõ áëüøèì îáúåìàì, çàìåòèì, ÷òî çíà÷åíèå ïîñòîÿííîé â ôîðìóëå (***) áóäåò óáûâàòü ïðè óâåëè÷åíèè îáúåìà. Ýòî îçíà÷àåò, ÷òî ïðÿìûå, èçîáðàæàþùèå èçîõîðû, îòâå÷àþùèå áëüøèì îáúåìàì, áóäóò ðàñïîëîæåíû áîëåå ïîëîãî. Èçîõîðû íà êîîðäèíàòíîé ïëîñêîñòè p T ïîêàçàíû íà ðèñ. 2, à (òîëñòûì ïóíêòèðîì èçîõîðû, îòâå÷àþùèå áîëüøåìó îáúåìó).
Àíàëîãè÷íîå ïðîâåäåííîìó âûøå ðàññìîòðåíèå èçîáàðè÷åñêîãî ïðîöåññà (p = const) ïðèâîäèò ê ãðàôèêàì (êîòîðûå íàçûâàþòñÿ èçîáàðàìè), èçîáðàæåííûì íà ðèñ. 3. Òîëñòûì ïóíêòèðîì íà ýòèõ ãðàôèêàõ ïîêàçàíû èçîáàðû, îòâå÷àþùèå áîëüøåìó äàâëåíèþ.
 øêîëüíîì êóðñå ôèçèêè íàèáîëåå ÷àñòî ðàññìàòðèâàþòñÿ èçîïðîöåññû, ò.å. ïðîöåññû, â êîòîðûõ îäèí èç ìàêðîñêîïè÷åñêèõ ïàðàìåòðîâ ãàçà íå èçìåíÿåòñÿ. Îäíàêî èçîïðîöåññû íå èñ÷åðïûâàþò âñå âîçìîæíûå ïðîöåññû ñ ãàçàìè. Ïðèâåäåì ïðèìåð.
Pages: | 1 | … | 2 | 3 |
| 5 | 6 | … | 28 |
Источник
