У шарового сосуда радиусом
1.Внимательно прочитать условие задачи.
2. Сделать краткую запись условий. Лучше все данные задачи сразу выразить в одинаковых величинах (СИ).
3. Написать уравнение или систему уравнений, отображающих происходящий физический процесс в общем виде.
4. Решить задачу в общем виде (получить “рабочую формулу”), т.е. выразить искомую величину через данные в задаче.
5.Произвести вычисления
6.Произвести проверку единиц величин, подставив их в “рабочую формулу”
Решение задач на построение графиков.
1.Изучить зависимость между величинами Р, V и Т.
2.Сделать запись зависимости для каждой линии графика.
3.Построить график.
Запомните : если вам дан на графике круговой процесс и надо построить этот процесс в иных координатных осях, то и на графиках, построенных вами, процесс тоже должен быть круговым, т. е. график тоже должен быть замкнут. Если на исходном графике изображен треугольник, то и на графиках построенного вами кругового процесса, каждая сторона которого соответствует одному из изопроцессов в газе неизменной массы, должен получиться тоже треугольник, за исключением построения графика в координатных осях Р-V, где изотерма имеет вид гиперболы.
Принято на графиках процессов в газах давление всегда откладывать по вертикальной оси (оси ординат), а температуру Т- по горизонтальной оси (оси абсцисс). Объем V в координатах Р –V откладывается по оси абсцисс, а координатах V-Т – по оси ординат.
Если масса газа неизменна, то продолжения графиков изобарного в координатах V- Т и изохорного в координатах Р-Т процессов непременно проходят через начало координат О.
Если на графиках в координатах V-Т и Р-Т продолжения отдельных участков изопроцесса в газе при постоянной массе не проходят через начало координат, а пересекают оси координат на некотором расстоянии от начала координат О, значит это не изопроцесс, т.е. при таком процессе изменялись все три параметра –Р,V и Т.
Примеры решения задач
Задача 1
Какое количество вещества содержится в алюминиевой отливке массой 5,4 кг?
Дано: СИ Решение
m (Al)=5,4 кг По таблице Менделеева определим
-?
(Al)=27
Количества вещества найдем по формуле:
; моль
Ответ:200 моль.
Задача 2.
Какой объем занимает 100 моль ртути?
Дано: СИ Решение
(Hg)=100 моль Объем ртути определим по формуле:
V-?
V=
(Hg)=13.6 10 Подставим m=
(Hg)=201 в фор-лу(1) V=
V= =1,5 *10 м
Ответ;1,5*10 или 1,5 л.
Задача 3.
Чему равно число молекул в 10 г. кислорода?
Дано: СИ Решение
m (O)=10 г0,01кг Молярную массу кислорода найдем по таблице
N-? Менделеева.
(O ) =32*10
Количества вещества определим из формул:
(1) (2) =>
откуда выразим N;
где Na=6.02*10 моль – постоянная Авогадро.N= =1,88*10
Ответ: N=1,88*10
Задача 4.
Какой объем занимают 2*103 молей идеального газа при температуре 270К и давлении 8*105 Па?
Дано: СИ Решение
ν =2*103 моль Согласно закону Клапейрона – Менделеева
Т = 270К РV =νRТ, откуда следует, что V = νRТ
Р = 8*105 Па Р
V – ? V = 2*103 *8,31*270 =5,6 м3
8*105
Ответ: V =5,6 м3
Задача 5.
В озеро, имеющее среднюю глубину 10м и площадь поверхности 20 км , бросили кристаллик поваренной соли массой 0,01г. Сколько молекул этой соли оказалось бы в наперстке воды объемом 2 см , зачерпнутой из озера, если полагать, что соль, растворившись, равномерно распределилась во всем объеме воды?
Решение
Дано: СИ
h=10м Чтобы найти число молекул N необходимо
S=20 км 2*10 определить объем озера V и количество N
m=0.01 г10 молекул соли находившихся в 0.01г
V =2 см 2*10 V=hS (1); N=
Na=6.02*10 N= 6.02 *1023 * = 1*1020молекул.
N -? Молярная масса поваренной соли равна 58г/моль Объем воды в озере
V=hS.V= 10*2*107 = 20*107 м3.
Определим, какую долю составляет объем наперстка V1 от всего объема воды в озере.
Для этого нужно V1/V = 2*10 /20*107 м3 =
1*10-14
Учитывая, что соль равномерна распределена в этом объеме можно найти значение N .
N1=N*( V1/V) = 1*1020 *1*10-14 = 1*106
Ответ: N1=1*106
Задача 6.
В баллоне емкостью 0,1м3 содержится углекислый газ при температуре 303К и давлении 20*105Па. Привести объем газа к нормальным условиям и найти массу газа.
Дано: СИ Решение
V1 = 0,1М3 Согласно уравнению Клапейрона
T1 = 303K Р1V1/T1 = P2V2/T2
P1 = 20*105Па откуда выразим значение V2 = Р1V1T2/P2T1
P2 = 1*105Па V2=20*105Па * 0,1М3 *273K/1*105Па *303K =
T2 = 273К = 1,8М3
V2- ? Молярная масса СО2 = 44*10-3 кг/моль.
m2- ? Используем уравнение Менделеева – Клапейрона.
PV = mRT/M откуда выразим
m = P2V2M/RT2
m =1*105Па *1,8М3*44*10-3 кг/моль/8,31Дж/моль*к *273К
= 3,49 кг
Ответ: V2=1,8 М3 m =3,49 кг.
Задача 7.
При какой температуре 0,08 кг кислорода в баллоне емкостью 20л создают давление 3*105Па?
Дано: СИ Решение
m=0,08кг Согласно закону Клапейрона – Менделеева
V= 20л20*10-3м3 Р V = , откуда следует, что T =
Р = 3*105 Па
M(O2) =32*10-3 кг/моль
T – ? T = 3*105 *20*10-3*32*10-3 =289K
8*10-2*8,31
Ответ: 289K
Задача 8.
В баллоне емкостью 0,1м3 содержится углекислый газ при температуре 303К и давлении 20*105Па. Привести объем газа к нормальным условиям и найти массу газа.
Дано: СИ Решение
V1 = 0,1М3 Согласно уравнению Клапейрона
T1 = 303K Р1V1/T1 = P2V2/T2
P1 = 20*105Па откуда выразим значение V2 = Р1V1T2/P2T1
P2 = 1*105Па V2=20*105Па * 0,1М3 *273K/1*105Па *303K =
T2 = 273К = 1,8М3
V2- ? Молярная масса СО2 = 44*10-3 кг/моль.
M2- ? Используем уравнение Менделеева – Клапейрона.
PV = mRT/M откуда выразим
m = P2V2M/RT2
m =1*105Па *1,8М3*44*10-3 кг/моль/8,31Дж/моль*к *273К
= 3,49 кг.
Ответ: V2=1,8 М3
Задача 9.
По графику процесса, осуществленного с идеальным газом (рис1), постройте график этого процесса в координатных осях Р, Т и V, Т.Температура газа в начальном состоянии была равна 250К.
Р*105
ПА
1 1
0 1 2 3 V, м3
Рис1
Решение
График показывает, что давление газа при переходе из состояния 1 в состояние 2 увеличилось в три раза, а объем в течение всего процесса оставался неизменным. Следовательно, процесс изменения состояния газа был изохорным. При изохорном процессе связь между давлением газа Р и абсолютной температурой Т выражается уравнением:
. Отсюда выразим Т2 = . Т2 = = 750 К
По известным начальным и конечным значения давления и температуры построим в системе координат с осями Р, Т точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления Р от температуры Т линейная, следовательно, график изохорного процесса в координатных осях Р, Т является прямой, проходящей через точки 1и 2 (рис2). В координатных осях V, Т график изохорного процесса – это отрезок прямой, параллельной оси абсцисс (рис 3).
Р*105,
ПА
3 2
1 1
0 250500750Т, К
Рис2
V, м3
3 1 2
0 250500750 Т,К
Рис3
Задача 10.
Один сосуд сферической формы радиусом R1 заполнен газом под давлением Р1, а в другом сосуде радиусом R2 – вакуум. Сосуды соединяют трубкой, объемом которой можно пренебречь. Какое давление Р2 установится в сосудах после соединения?
Дано Решение
R1 После того как сосуды соединили трубкой в них установится
Р1 одинаковое давление Р2. Температура не изменилась, следовательно
R2 процесс изотермический. Применяем закон Бойля-мариотта.
Т- const Р1V1 =Р2(V1 + V2) (1)
Р2 – ? Здесь V1 = – объем одного шара,
V2= – объем второго шара.
Подставив в уравнение (1) выражения объемов сосудов через их радиусы, получим Р1* = Р2(
Р1 = Р2( ). (2)
Из уравнения (2) найдем давление Р2 .
Р2=
Ответ:Р2=
Читайте также:
Рекомендуемые страницы:
©2015-2020 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-01-11
Нарушение авторских прав и Нарушение персональных данных
Источник
Часть 3-1 Силы давления покоящейся жидкости на криволинейные стенки
Задача (Куколевский И.И.) 3-1. Определить величины и направления сил давления воды на плоское и полусферическое днища цилиндрическою сосуда диаметром D=1 м в трех случаях:
y=+D/5, y=-D/5, y=0
Показать на чертеже горизонтальные и вертикальные составляющие и полные силы давления воды на днища.
Ответ. Горизонтальные составляющие сил давления на правое и левое днища одинаковы и равны + 1,54 кН; – 1,54 кН и 0; вертикальные составляющие сил давления на полусферу одинаковы для трех случаев и равны 2,57 кН.
Скачать решение задачи 3-1 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-2. В прямоугольном окне вертикальной стенки резервуара установлен на цапфах цилиндрический затвор диаметром D = 0,8м и длиной В = 3м.
1) Определить усилие на цапфы и момент от воздействия воды на затвор в изображенном на эскизе положении при напоре Н=1 м.
2) Каковы будут усилие на цапфы и момент, если повернуть затвор на 180°.
Ответ. 1) Усилие на обе цапфы Р = 23,8 кН; момент от воздействия жидкости М =628 Н*м; 2) Р= 24,7кН; М = 0.
Скачать решение задачи 3-2 (Куколевский И.И.) (цена 80р)
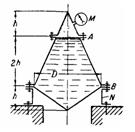
Задача (Куколевский И.И.) 3-3. Показание манометра, присоединенного к днищу бака, равно M = 10 кПа. Найти давление воздуха, находящегося над водой, если h1 = 1,8 м и h2 = 1 м.
Определить, растягивающее и срезающее усилия болтов, крепящих к вертикальной стенке бака коническую крышку с. размерами d = 0,8м и l = 0,6м; весом крышки пренебречь. Построить график зависимости этих сил от давления М.
Ответ. рх=-17,5 кПа (разрежение); Pраст = – 3,82 кН (крышка прижимается к баку давлением снаружи), Pсрез = 0,98 кН.
Скачать решение задачи 3-3 (Куколевский И.И.) (цена 80р)
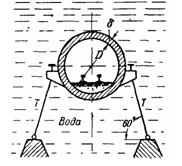
Задача (Куколевский И.И.) 3-4. Цилиндрический затвор диаметром D = 1,2 м и длиной L= 16 м, масса которого 40 т, может открываться путем качения его вверх цепью по наклонным направляющим, составляющим угол а = 70° с горизонтом.
Определить по величине и направлению силу давления воды на закрытый затвор. Найти натяжение цепи при трогании затвора с места и при выходе его из воды. Как изменятся сила давления воды на затвор и натяжение цепи, если уровень воды за плотиной поднимется до оси затвора?
Ответ. Р= 144 кН; угол с горизонтом 38°10′; Х=123 кН при трогании и 184 кН при выходе из воды.
Скачать решение задачи 3-4 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-5. Определить силу Q, прижимающую стальной (относительная плотность б = 8) шаровой всасывающий клапан радиусом R=100мм к седлу, имеющему дчаметр d = 125 мм, если диаметр насосного цилиндра D = 350 мм, а усилие по штоку P = 4000 Н. Седло клапана расположено ниже оси цилиндра на расстоянии h1 = 0,5 м и выше свободной поверхности резервуара с атмосферным давлением на расстоянии h2 = 6,5 м, причем труба под клапаном заполнена водой.
Ответ. Q= 1640 Н.
Скачать решение задачи 3-5 (Куколевский И.И.) (цена 80р)
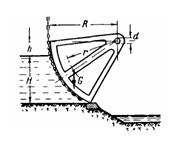
Задача (Куколевский И.И.) 3-6. Секторный затвор радиусом R = 5м и длиной L= 4,5м поддерживает напор воды Н = 3,5м. Для пропуска воды затвор поднимается цепью, поворачиваясь вокруг горизонтальной осина цапфах диаметром d=150мм. Масса затвора равна 3 т, его центр тяжести расположен на радиусе r= 0,75R. При закрытом затворе ось его вращения и верхний обрез сектора лежат в одной горизонтальной плоскости, расположенной выше свободной поверхности на расстоянии h=1 м.
1) Определить силу, нагружающую подшипники закрытого затвора.
2) Найти силу N, прижимающую затвор к порогу.
3) Начальное натяжение цепи при подъеме затвора (коэффициент трения в цапфах принять f = 0,3).
Ответ. 1) Р = 398 кН; угол с горизонтом 47°; 2) N = 42,8 Н, 3) Q = 20,5 кН.
Скачать решение задачи 3-6 (Куколевский И.И.) (цена 80р)
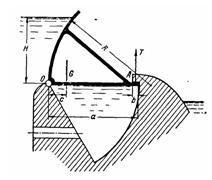
Задача (Куколевский И.И.) 3-7. Секторный затвор плотины радиусом R = 4,5 м поддерживает напор воды Н = 3м. Поворачиваясь вокруг оси О, затвор может погружаться в выемку, сделанную в теле плотины и заполненную водой. Пренебрегая трением в опорах вращения, определить усилие Т, с которым затвор прижимается к уступу А плотины (приходящееся на 1 м, длины затвора), если масса 1 пог. м затвора 1т, размеры а = 4м и b= 0,3 ми расстояние с = 0,6 м.
Ответ. Т = 47,1 кН.
Скачать решение задачи 3-7 (Куколевский И.И.) (цена 80р)
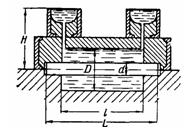
Задача (Куколевский И.И.) 3-8. Горизонтальный цилиндрический сосуд диаметром d = 0,8м с полусферической и конической тонкостенными крышками заполнен жидкостью плотностью ρ1. Правая половина цилиндра (с конической крышкой) вставлена в замкнутый резервуар и находится под уровнем другой жидкости (удельного веса уа) на глубине а = 2м. Определить горизонтальные и вертикальные составляющие сил давления жидкости на полусферическую и коническую крышки А и В, если показание вакуумметра V = 10 кПа, показание манометра М = 30 кПа и ρ1=ρ2=1000 кг/м3. Показать на чертеже горизонтальные и вертикальные составляющие и полные силы давления жидкости на полусферу и конус. Как изменятся силы при ρ1= 0,8 ρ1= 800 кг/м3?
Ответ. Для полусфера Рг =- 5,03 кН и Рв=1,31 кН; для конуса РГ = – 30 кН и Рв = 0; при Рв = 0,8 ρ1=0,8 ρ2 = 800 кг/м3 горизонтальные составляющие не измелятся; вертикальная составляющая яа полусферу Р’в=1,05кН, на конус Р’В = – 0,263 кН.
Скачать решение задачи 3-8 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-9. Отверстие в дне сосуда, содержащего масло (δ = 0,83), закрыто конической пробкой с размерами D=100мм, d = 50 мм и а = 100мм, укрепленной на штоке d1 = 25 мм. Уровень масла расположен выше пробки на расстоянии b = 50 мм. Собственным весом пробки и трением в сальнике пренебречь.
1) Определить начальное усилие Р, необходимое для подъема пробки при показании манометра М = 10 кПа.
2) Давление воздуха в сосуде, пои котором усилие Р окажется равным нулю.
Ответ. 1) P=13,5 кН; 2) ри = 1,04 кПа.
Скачать решение задачи 3-9 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-10. Определить усилия, нагружающие болтовые группы А и В сборного конического резервуара, содержащего воду, если h = 1м, наибольший внутренний диаметр сосуда D = 3м, а показание манометра М = 40 кПа.
Ответ. РA = 31,4 кН; РB = 355 кН.
Скачать решение задачи 3-10 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-11. Определить усилия, нагружающие болтовые группы А, В и С симметричного сосуда размерами D1=1,8м, D2 = 0,9 и h = 1,2м. m1 = 600 кг и m2 =900 кг – массы крышки и конической обечайки сосуда. Сосуд заполнен водой, избыточное давление М = 50 кПа. Как изменятся усилия на болты, если вместо указанной на эскизе опоры подвесить сосуд за верхнюю крышку?
Ответ. РА=121 кН; Рв = 7,1 кН, Рс=128 кН, PA/=185 кН; Р’в = 71,5 кН; Р’с= 192 кН.
Скачать решение задачи 3-11 (Куколевский И.И.) (цена 80р)
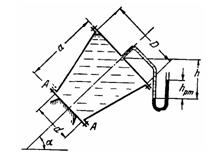
Задача (Куколевский И.И.) 3-12. Определить растягивающие Рраст и срезающие Рсрез усилия, нагружающие болты фланца А конического резервуара размерами D=1 м; d = 0,5м и а=1 м, заполненного жидкостью удельного веса р = 750 кг/м3. Давление в резервуаре измеряется ртутным манометром, показание которого hрт = 0,3м и Н = 6,5 м Угол наклона оси резервуара к горизонту а = 45° собственный вес резервуара не учитывать.
Ответ. Рраст = 576 кН; Рсрез = 2,38 кН.
Скачать решение задачи 3-12 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-13. Отформован и заливается чугуном (δчуг=7) полый барабан диаметром D = 250 мм и длиной l = 1м. Для получения внутреннего отверстия в форму заложен цилиндрический стержень (С = 2,5) диаметром d = 80 мм и длиной L= 1,2м. Уровень чугуна в литнике расположен на высоте Н = 0,5м над осью формы.
1) Определить максимальный изгибающий момент Мmax, действующий на стержень при заливке формы.
2) Вертикальную силу, которая стремится поднять, опоку при заливке формы. Стержень при отливке рассматривать как балку, свободно лежащую на двух опорах. Влиянием литников на искомую силу пренебречь.
Ответ. Мизг = 33,4 кН*м; Р = 7,12 кН.
Скачать решение задачи 3-13 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-14. Шаровой сосуд радиусом R=0,4 м, заполненный водой, висит на тяге, прикрепленной к его верхней половине. Какое наименьшее давление в центре сосуда (показание пружинного мановакуумметра П) удержит свободную нижнюю половину сосуда весом m=150кг?
Ответить на поставленный вопрос, считая сосуд невесомым.
Ответ. Разрежение в центре: V1=5,55 кПа; V2= 2,62 кПа.
Скачать решение задачи 3-14 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-15. Каков наименьший уровень Н воды в сосуде, при котором стальной шар (δ = 8) радиусом R=100мм, перекрывающий круглое отверстие диаметром d=1,5R в вертикальной стенке, будет находиться в равновесии?
Ответ. H=1,48 м
Скачать решение задачи 3-15 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-16. Определить усилия, растягивающие и срезающие болты диаметрального фланцевого соединения шарового сосуда радиусом R = 0,4 м, заполненного наполовину водой и находящегося под внутренним давлением сжатого газа М = 20 кПа. Плоскость стыка наклонена к горизонту под углом а =45°, вес полушара m = 300 кГ.
Ответ. Растягивающее усилие 7,98 кН; срезающее усилие 2,32 кН .
Скачать решение задачи 3-16 (Куколевский И.И.) (цена 80р)
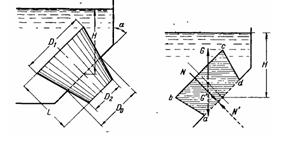
Задача (Куколевский И.И.) 3-17. Отверстие диаметром D0 = 200 мм в плоской стенке, наклоненной к вертикали под углом а = 45°, перекрыто конической пробкой, размеры которой D1 = 300 мм, D2=150мм и l = 300 мм. Уровень воды в сосуде Н = 500мм. Определить силу давления воды на пробку.
Указание. Помимо общего способа нахождения сил по двум заданным направлениям, силу давления на смоченную поверхность пробки аЬсЛ можно определить при помощи следующего приема предположив, что жидкость находится с противоположной стороны этой поверхности (при том же уровне Я), найдем из условия равновесия заштрихованного объема .фиктивной” жидкости, что сила ее давления на рассматриваемую поверхность равна
P=N+G
где N – сила давления на плоскую стенку аd
G – вес заштрихованного объема жидкости, Так как сила давления на каждый элемент поверхности определяется глубиной его погружения под уровнем жидкости, замена действительной жидкости фиктивной не меняет величины силы давления на поверхность, но изменяет ее направление на противоположное. Следовательно, искомая сила давления Р равна:
P=N+G
где N = -N и G=-G.
Ответ. Слагающая Р, нормальная плоскости отверстия Р1= 85,3 Н, а параллельная плоскости отверстия Р2 =68,7 Н.
Скачать решение задачи 3-17 (Куколевский И.И.) (цена 80р)
Часть 3-2 Силы давления покоящейся жидкости на криволинейные стенки
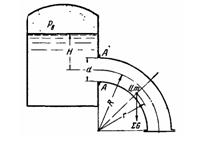
Задача (Куколевский И.И.) 3-18. Определить отрывающее Ропр и сдвигающее Рсдв усилия и изгибающий момент на фланце А, крепящем колено 90° к баку, если разрежение воздуха в баке Pв = 10 кПа и глубина H= 1,8 м. Диаметр колена d = 400 мм., его радиус кривизны R= 1 м и масса m = 100 кг. Центр тяжести колена, заполненного водой, принять расположенным на биссектрисе в точке r =0,9*R. Как влияет величина давления воздуха в сосуде на искомые усилия и момент?
Ответ. Ропр = 0,96 кН; Рсдв = 2,92кН Момент M=1850 кН*м
Скачать решение задачи 3-18 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-19. В цилиндрическом сосуде плавает кусок льда относительного веса δ1 = 0,9, в который впаян стальной шарик относительного веса δ2 = 7,8. Объем льда V1 = 12 дм3, объем шарика V2 = 50 см3.
1) Какая часть объема тела находится над водой?
2) Как изменится уровень Н в сосуде, когда лед растает, если диаметр сосуда D = 500 мм?
Ответить на поставленные вопросы еще для следующих двух вариантов задачи:
1) Вместо стального шарика объем V2 заполнен льдом.
2) Объем V2 представляет воздушную полость.
Ответ. Vх = 0,86 л; уровень понизится на 1,73 мм.
Скачать решенио задачи 3-19 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-20. В сосуд, заполненный водой и маслом (ρм = 900 кг/м3), погружен кусок воска (ρВ = 960 кг/м3). Определить, какая часть объема воска погрузится в воду и какая останется в масле?
Ответ. В воду погрузится 0,6 объема воска.
Скачать решение задачи 3-20 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-21. 1) Прямоугольный параллелепипед относительного веса δ = 0,7 со стороной квадратного основания а =250 мм и высотой b плавает в воде. Какому условию должна удовлетворять высота b, чтобы равновесие плавающего параллелепипеда было устойчивым? 2) В той же жидкости плавает куб со стороной а. Какому условию должен удовлетворять относительный вес б материала куба, чтобы равновесие плавающего куба было устойчивым?
Ответ. 1) b < 0,222 м; 2) δ ни должно быть в пределах 0,211-0,789 и не может быть больше 1, так как в этом случае куб потонет.
Скачать решение задачи 3-21 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-22. На понтоне с размерами дна 12*4 м, высотой борта 1,2м и массой 8 т перевозят котел массой 16 т, центр тяжести которого расположен на высоте 1 м над палубой понтона.
1) Определить глубину х погружения понтона при установке котла на середине понтона.
2) Найти максимальный момент Мизг, изгибающий поперечное сечение корпуса понтона.
3) Подсчитать момент устойчивости Муст при боковом крене 0= 1СР.
Считать вес понтона распределенным равномерно по всему дну, а центр тяжести его поперечных сечений расположенным на 0,8 м ниже палубы.
Ответ. х = 0,5м; Мизг = 235 кН-м, Муст =51 кН-м.
Скачать решение задачи 3-22 (Куколевский И.И.) (цена 80р)
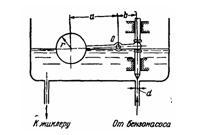
Задача (Куколевский И.И.) 3-23. Бензин (δ = 0,7) под давлением р = 30 кПа подводится к поплавковой камере карбюратора по трубке диаметром d= 4 мм. Шаровой поплавок весом 25 г и игла (вес в бензине 12 г), перекрывающая доступ бензина, укреплены на рычаге (а = 40мм, b=15мм), который может поворачиваться вокруг неподвижной оси О. Определить радиус r поплавка из условия, чтобы в момент открытия отверстия поплавок был погружен наполовину (трением в шарнирах и весом рычага пренебречь).
Ответ, r =28,7мм.
Скачать решение задачи 3-23 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-24. Погруженный в воду полый шаровой клапан диаметром D = 150 мм и массой m = 0,5кг закрывает выходное отверстие внутренней трубы диаметром d =100мм. При какой разности уровней Н клапан начнет пропускать воду из внутренней трубы в резервуар?
Ответ. Н = 161 мм.
Скачать решение задачи 3-24 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-25. Подводный железобетонный туннель круглого сечения с внутренним диаметром D = 3м и толщиной стенки δ = 250 мм удерживается от всплывания тросами, расположенными попарно через каждые 6 м длины туннеля. Определить натяжение тросов, полагая вес 1 пог. м дополнительной нагрузки туннеля m = 1000 кГ и удельный вес бетона 2,5 т/м3.
Ответ. 75,5 кН на один трос.
Скачать решение задачи 3-25 (Куколевский И.И.) (цена 80р)
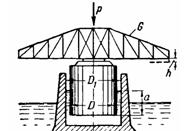
Задача (Куколевский И.И.) 3-26. Поворотный пролет моста опирается на цилиндрический поплавок диаметром D= 3,4 м, плавающий в камере диаметром D1 = 3,6 м.
1) Определить погружение а поплавка в воду, если масса пролета с поплавком m = 30 т.
2) Осадку Н пролета при нагружении его внешней силой Р= 100 кН.
Ответ, а = 3,3м; h = 0,12м.
Скачать решение задачи 3-26 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-27. Деревянный брус постоянного сечения (относительный вес δ = 0,75) длиной L = 2м подвешен на шарнире без трения и своим нижним концом погружен в воду. Определить, при какой глубине погружения г, вертикальное положение бруса будет устойчивым. Найти глубину z2, при которой брус будет иметь наклон а= 60 к вертикали.
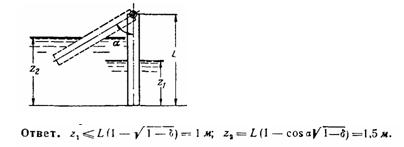
Скачать решение задачи 3-27 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-28. Однородный брус постоянного сечения F, длиной L и плотностью ρ1, своим нижним концом шарнирно закреплен на глубине Н<L под свободной поверхностью жидкости с удельным весом ρ > ρ1.
1) Определить какой угол наклона φ отвечает устойчивому равновесию бруса в жидкости и при каких значениях L/Н брус будет покоиться в вертикальном положении?
2) Какова при равновесном положении бруса опорная реакция К в шарнире.
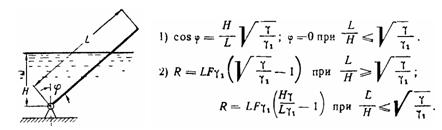
Скачать решение задачи 3-28 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 3-29. Тонкостенный цилиндрический колокол микроманометра свободно подвешен на шарнире и частично погружен открытым концом под постоянный уровень жидкости с атмосферным давлением. Определить, какова должна быть высота а расположения точки подвеса колокола над уровнем жидкости, чтобы при его отклонениях на углы Θ <10 от вертикали он возвращался в исходное положение равновесия. Диаметр колокола D = 70 мм, его масса m = 800 т, расстояние центра тяжести до точки подвеса b = 200 мм. Избыточное давление внутри колокола Pи =1 кПа, плотность жидкости (спирт) ρ = 800 кг/м3.
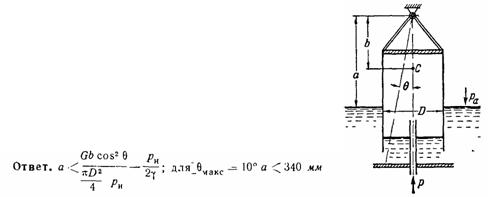
Скачать решение задачи 3-29 (Куколевский И.И.) (цена 80р)
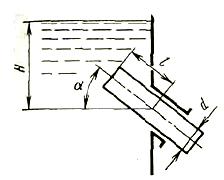
Задача (Куколевский И.И.) 3-30. Определить горизонтальную Рг и вертикальную Рв силы давления воды на наклонно выставленный внутрь резервуара на растоянии l=1м цилиндр диаметром d = 400мм, если напор Н = 1м и угол наклона цилиндра к горизонту α = 45°.
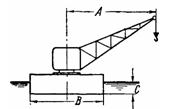
Задача (Куколевский И.И.) 3-31. На барже с размерами дна L*B = 60*10 м и осадкой С =1,5 м установлен кран грузоподъемностью 5 т с максимальным вылетом стрелы A=15 м. Определить угол крена баржи при максимальной нагрузке крана, если центр тяжести системы расположен выше дна баржи на 4,25 м.
Ответ, угол = 2° 20′.
Скачать решение задачи 3-31 (Куколевский И.И.) (цена 80р)
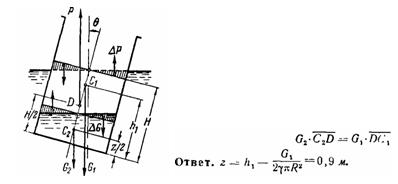
Задача (Куколевский И.И.) 3-32. Тонкостенный цилиндрический сосуд радиусом R = 0,8 м и весом m1 = 2,4 т с центром тяжести, расположенным на расстоянии h1= 1,5 м от дна, плавает в воде. Определить, какова должна быть минимальная высота г слоя воды, залитой внутрь сосуда, чтобы он обладал статической устойчивостью. Указание. При отклонении оси плавания сосуда от вертикали на малый угол 6 на сосуд действуют (см. рис. к решению задачи): 1) сила его веса G1 сила веса залитой в него воды Ог и выталкивающая сила Р = G1 + m2, проходящие соответственно через центр тяжести сосуда С1, центр тяжести залитой воды С2 и центр водоизмещения сосуда D (точки С1 и D отвечают вертикальному положению сосуда);
2) моменты от дополнительных подъемных сил ΔР и сил веса залитой воды dG, возникающие вследствие наклона сосуда, одинаковы по величине, но противоположны по знаку и поэтому не влияют на условия равновесия. Отсюда для устойчивости равновесия необходимо:
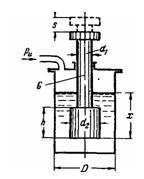
Задача (Куколевский И.И.) 3-33. Ступенчатый шток с размерами d1= 100 мм, d2 = h = 300 мм и массой m = 24 кг плавает в воде, заполняющей цилиндрический сосуд диаметром D = 400 мм. В пространстве над водой может быть установлено любое заданное давление воздуха.
1) Определить глубину погружения x6 штока при атмосферном давлении над уровнем воды.
2) Определить, при каком избыточном давлении ри шток выйдет из воды и каково будет при этом его перемещение S от начального положения при ри = 0? Построить график зависимости S=f(ри).
Ответ. 1) x = 657 мм. 2) Рн = 30 кПа и s = 466 мм.
Скачать решение задачи 3-33 (Куколевский И.И.) (цена 80р)
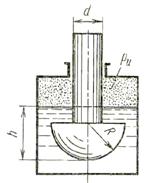
Задача (Куколевский И.И.) 3.34. Тело в форме цилиндра с полушаровой головкой, размеры которого d = 200 мм, R = 300 мм и масса m = 230 кг, плавает а воде, заполняющей замкнутый сосуд. Установить зависимость между избыточным давлением Ризб, газа в сосуде и погружением h тела под уровнем волы и найти давление, при котором погружение станет равным Н = R и полушар начнет выходить из воды.
Ответ. Pн = 54 кПа.
Скачать решение задачи 3-34 (Куколевский И.И.) (цена 80р)
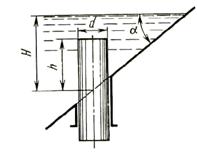
Задача (Куколевский И.И.) 3.35. Определить горизонтальную Рг и вертикальную Рв силы давления воды па вертикальный цилиндр диаметром d = 400 мм, вставленный через отверстие в наклонной стенке (а = 45) внутрь резервуара на высоту h= 1 м. Уровень воды H = 1,6м.
Ответ. Рг = 1.95 кН: Рв = 0.735 кН.
Скачать решение задачи 3-35 (Куколевский И.И.) (цена 80р)
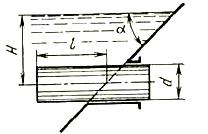
Задача (Куколевский И.И.) 3.36. Определить горизонтальную Рг и вертикальную Рв силы давления воды на горизонтальный цилиндр диаметром d = 400 мм, который вставлен через отверстие в наклонной стенке (а = 45°) внутрь резервуара на расстояние l = 1000 мм. Уровень воды над осью цилиндра Н = 1 м.
Ответ. Рг = 1.23 кН; Рв = 0.
Скачать решение задачи 3-36 (Куколевский И.И.) (цена 80р)
Источник
