У тебя есть два пустых сосуда


Задача 1
Для разведения картофельного пюре быстрого приготовления “Зеленый великан” требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?
Задача 2
Как с помощью 2-литровой и 5-литровой банок отмерить ровно 1 литр?
Задача 3
Как, имея пятилитровое ведро и девяти литровую банку, набрать из реки ровно три литра воды?
Задача 4
Для марш-броска по пустыне путешественнику необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, выдают только 5-литровые фляги, а также имеются 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?
Задача 5
Есть два кувшина емкостью 5 л и 9 л. Нужно набрать из источника 7 л воды, если можно пользоваться только кувшинами.
Задача 6
Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?
Задача 7
Деление 10 л поровну, имея сосуды 3, 6 и 7 л.
Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами.
Какое наименьшее количество переливаний потребуется?
Задача 8
Деление 8 л поровну, имея сосуды 8, 5 и 3 л.
Разделить на две равные части воду, находящуюся в полном 8 литровом сосуде, пользуясь этим и пустыми 5- и 3-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?
Задача 9
Деление 16 л поровну, имея сосуды 6, 11 и 16 л.
Разделить на две равные части воду, находящуюся в полном 16 литровом сосуде, пользуясь этим и пустыми 11- и 6-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?
Задача 10
Два сосуда и кран с водой.
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л?

Задача 11
Рядом с лабораторией протекает бурная река. Как при помощи двух бочек объёмом 3 и 5 галлонов отмерить ровно 4 галлона речной воды?
Задача 12
У Цепустролиса есть нерастворимая колба, в которой содержится 12 миллилитров серной кислоты, а также две нерастворимые мензурки объёмом 5 и 7 миллилитров. Как ему получить две порции по 6 миллилитров серной кислоты, необходимых для опыта? (Кислота растворит любую другую посуду в лаборатории.)
Указание Решение
Задача 13
Однажды алхимику удалось в одном сосуде собрать и смешать 8 слезинок саламандры (важнейшую алхимическую субстанцию). У него есть два пустых флакона объёмом 2 и 3 слезинки. Как ему отмерить 4 слезинки? Не забывайте, что слёзы высыхают очень быстро! У Цепустролиса есть время только на три переливания, прежде чем редкое вещество испарится.
Задача 14
Еще одним важным элементом эликсира является кровь кобры. В чаше собрано 10 ложек змеиной крови. Имеются ковши объемом 3 ложки и 4 ложки. Как ученому получить 5 ложек крови? Решая задачу, помните, что нужно сделать не более 5 переливаний, иначе драгоценная кровь свернётся и перестанет быть годной.
Задача 15
В подвале лаборатории растут мандрагоры и имеется неограниченный запас мандрагорового экстракта. Как при помощи мензурок из задачи №2 отмерить 4 миллилитра мандрагорового экстракта? Но берегитесь! Если ни на одном из этапов ни в одной из мензурок не окажется ровно 3 миллилитра экстракта, мандрагоры закатят истерику и криками разрушат лабораторию!
Задача 16
В лабораторной печи находится котел, в котором бурлит 9 литров расплавленного олова. В процессе эксперимента нужно через равные промежутки времени трижды добавлять в эликсир по 3 литра олова. Как осуществить это, если в наличии только три огнеупорных кубка объемом 5, 4 и 2 литра? (То есть нужно иметь в какой-то момент 3 порции по 3 литра.)
Задача 17
Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?
Задача 18
Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?
Задача 19
Бэтмен и Человек-Паук никак не могли определить, кто из них самый главный супергерой. Что только они не делали: отжимались, бегали 100 метровку, подтягивались – то один победит, то другой. Так и не разрешив свой спор, отправились они к мудрецу. Мудрец подумал и сказал: «Самый главный супергерой – это не тот, кто сильнее, а тот, кто сообразительнее! Вот, кто решит первым задачу, тот и будет самым-самым! Слушайте: имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л живой воды?» Помогите вашему любимому герою решить эту задачу.
Задача 20
Бидон емкостью 10 л наполнен парным молоком. Требуется перелить из этого бидона 5 л молока в семи литровый бидон, используя при этом трехлитровый бидон.

Задача 21
Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами. Какое наименьшее количество переливаний потребуется?
Задача 22
Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьми литровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов?
Задача 23
У подножья высокого холма, на берегу тихой речки был небольшой аул. Жили в нем два брата-охотника. Старшего брата звали Каалка, младшего Копчон. Отправляет старший брат младшего за водой и дает ему два бурдюка, вместимостью 8л и 5л и просит принести ровно 7л воды. Сможет ли Копчон выполнить просьбу старшего брата?
Задача 24
Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?
Задача 25
Губке Бобу срочно нужно налить из водопроводного крана 6 л воды. Но он имеет лишь два сосуда 5-литровый и 7-литровый. Как ему это сделать?
Задача 26
Имеются шести литровая банка сока и две пустые банки: трех- и четырехлитровая. Как налить 1 литр сока в трехлитровую банку?
Задача 27
Двое должны разделить поровну 8 ведер кваса, находящегося в восьмиведерном бочонке. Но у них есть только два пустых бочонка, в один из которых входит 5 ведер, а в другой – 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками?
Задача 28
Имеются три бочонка вместимостью 6 вёдер, 3 ведра и 7 вёдер. В первом и третьем содержится соответственно 4 и 6 ведёр кваса. Требуется, пользуясь только этими тремя бочонками, разделить квас поровну.
Задача 29
Три человека купили сосуд, полностью заполненный 24 унциями бальзама. Позже они приобрели три пустых сосуда объемом 5, 11 и 13 унций. Как они могли бы поделить бальзам на равные части используя эти четыре сосуда? Постарайтесь решить задачу за наименьшее количество переливаний.
Задача 30
Имеются трёхлитровая банка сока и две пустые банки: одна – литровая, другая – двухлитровая. Как разлить сок так, чтобы во всех трёх банках было по одному литру?
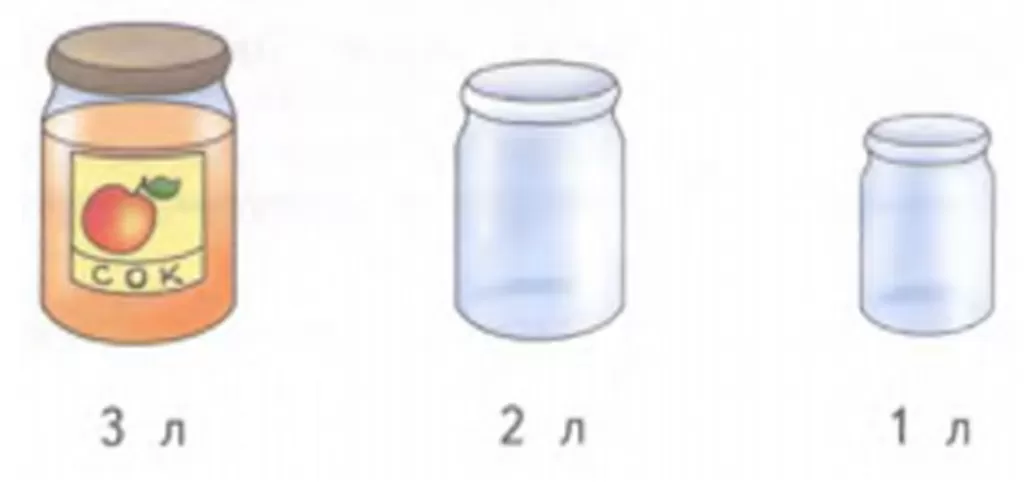
Задача 31
В одном порту моряк пришел в лавку с пустым бочонком на пять галлонов и попросил лавочника налить туда четыре галлона отборного ямайского рома. К несчастью, единственным сосудом для измерения был старый оловянный кувшин на три галлона. Как лавочник сумел точно отмерить четыре галлона с помощью этих двух емкостей?
Задача 32
К продавцу, студенту-математику, подрабатывющему летом торговлей у бочки с квасом, подходят два веселых приятеля и просят налить им по литру кваса каждому. Продавец замечает, что у него есть лишь две емкости, трехлитровая и пятилитровая, и он не может выполнить их просьбу. Приятели предлагают 100 долларов, если продавец сможет выполнить их заказ, причем выдать им порции продавец должен одновременно. После некоторого размышления, продавец сумел это сделать. Каким образом? Заметим, что при переливаниях квас не теряется и что полные емкости позволяют точно отмерять объемы 3 и 5 литров.
Задача 33
Винодел обычно продает свое вино по 30 и по 50 литров и использует для этого кувшины только такого размера. Один из покупателей захотел купить 10 литров. Как винодел отмерил ему 10 литров пользуясь своими кувшинами?
Задача 34
Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л?
Задача 35
Шрек решил сделать Фионе подарок на день рождения – приготовить суп, о котором она мечтала уже давно. Рецепт этого супа он нашел в поваренной книге, но возникла небольшая проблема: нужно налить в кастрюлю ровно 5 л воды. Но как это сделать, если у Шрека 7-литровое ведро и 3-литровая банка? Помогите своему любимому герою исполнить мечту Фионы.
Задача 36
У Гарри Потера имеются двое песочных часов: на 7 минут и на 11 минут. Волшебное зелье должно варится 15 минут. Как сварить его Гарри Потеру, перевернув часы минимальное количество раз?
Задача 37
Летом Винни-Пух сделал запас меда на зиму и решил разделить его пополам, чтобы съесть половину до Нового Года, а другую половину – после Нового года. Весь мед находится в ведре, которое вмещает 6 литров, у него есть 2 пустые банки – 5-литровая и 1-литровая. Может ли он разделить мед так, как задумал?
Задача 38
У Белоснежки есть полное восьми литровое ведро компота. Как ей отлить 4 л с помощью пустых трехлитровой банки и пятилитрового бидона?
Задача 39
Хозяин имеет четыре бочки А, В, С и Д, причем бочки С и Д одинаковой вместимости. Пусть бочки А и В наполнены квасом, если содержимым бочки А наполнить бочку С, то в бочке А останется 1/5 ее содержимого, если же содержимым бочки В наполнить бочку Д, то в бочке В останется 1/9 ее содержимого. Пусть бочки С и Д наполнены квасом; чтобы наполнить бочки А и В, надо взять содержимое бочек С и Д и добавить еще 9 ведер кваса. Сколько ведер кваса вмещает каждая бочка?
Задача 40
Из ведра, содержащего 5 литров воды, отливают 1 литр, а затем в ведро вливают 1 литр сока. Перемешав все это, из ведра отливают 1 литр смеси, затем в ведро опять вливают 1 литр сока. Опять перемешивают, отливают 1 литр смеси и вливают 1 литр сока. Сколько в ведре после этого останется воды?
Задача 41
Из бочки, содержащей 100 литров сока, отливают 1 литр и вливают в нее затем 1 литр воды. Перемешав полученную смесь, из бочки отливают 1 литр смеси и опять вливают в нее 1 литр воды. Перемешав полученную смесь, из бочки опять отливают один литр смеси и вливают 1 литр воды, и так делают неоднократно. Можно ли в результате таких операций получить смесь, содержащую 50 литров воды и 50 литров сока?
Задача 42
Две группы альпинистов готовятся к восхождению. Для приготовления еды они используют примусы, которые заправляют бензином. В альплагере имеется 10-литровая канистра бензина. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить бензин в два сосуда по 5 литров в каждом?
Задача 43
Разбойники раздобыли 10 унций (1 унция – примерно 30 см 3 ) золотого песка. У них имеется две пустые коробки, емкостью 6 и 4 унции. Как им разделить песок пополам? Если на одно пересыпание требуется 1 минута, то сколько времени они будут делить свою добычу?
Задача 44
Отлейте из цистерны 13 л молока, пользуясь бидонами емкостью 17 л и 5 л.

Задача 45
Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?
Задача 46
Для разведения картофельного пюре быстрого приготовления “Зеленый великан” требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?
Задача 47
В походе приготовили ведро компота. Как, имея банки, вмещающие 500 г. и 900 г. воды, отливать компот порциями по 300 г?
Задача 48
Нефтяники пробурили скважину нефти. Необходимо доставить в лабораторию на экспертизу 6 литров нефти. В распоряжении имеется 9-литровый и 4-литровый сосуды. Как с помощью этих сосудов набрать 6 литров?
Задача 49
Взгляни на берег – там ты увидишь две банки. В одну из них помещается ровно два литра воды, а в другую – три. Как налить в двухлитровую банку точно один литр? Укажи два способа.
Задача 50
Есть три бидона емкостью 14, 9 и 5 литров. В большом бидоне 14 л молока, остальные пусты. Как с помощью этих бидонов разделить молоко пополам?
Задача 51
Имеется три сосуда без делений объемами 6 л, 7 л, 8 л, кран с водой, раковина и 6 л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 12 л смеси воды с сиропом, так чтобы в каждом сосуде воды и сиропа было поровну?
Задача 52
Имеются два сосуда вместимостью 7 и 11 литров и большая бочка, наполненная водой. Как с помощью этих двух сосудов отмерить ровно 2 литра воды?
Задача 53
Имеются три сосуда вместимостью 8, 5 и 3 литра. Наибольший сосуд полон молока. Как разделить это молоко на две равные части, используя остальные сосуды?

Задача 54
У подножья высокого холма, на берегу тихой речки был небольшой аул. Жили в нем два брата-охотника. Отправляет старший брат младшего за водой и даёт ему два бурдюка, вместимостью 8л и 5л и просит принести ровно 7л воды. Как это сделать?
Задача 55
Для марш-броска по пустыне путешественнику необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, выдают только 5-литровые фляги, а также имеются 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?
Задача 56
Наберите 1 литр воды в любом из сосудов. Объемы сосудов – 5 и 3 литра.
Задача 57
Наберите 1 литр воды в любом из сосудов. Объемы сосудов – 8 и 5 литров.
Задача 58
Наберите 7 литров воды. Объемы сосудов – 6, 10, 15 литров.
Задача 59
Наберите 1 литр воды. Объемы сосудов – 6 и 10 литров, в первом сосуде налито 3 литра.
Задача 60
Богатырь подошел к реке с двумя ведрами, вмещающими 15 литров и 16 литров. Удастся ли ему налить (отмерить) при помощи этих ведер ровно 8 литров воды?
Задача 61
Молочница принесла молоко в восьми литровом ведре, а у бабушки имеется только одна трехлитровая банка и одно четырехлитровое ведро. Как ей взять у молочницы 4 литра молока?
Задача 62
Отлейте из бочки ровно 13 литра кваса при помощи двух бидонов: один емкостью 17 литров, а другой емкостью 5 литров.
Задача 63
Бочка вмещает 12 ведер воды. Для полива с вечера ее наполнили до верху. Имеются две пустые бочки, вмещающие 5 ведер и 8 ведер воды. Разлейте содержимое бочки поровну.

Задача 64
В канистре не менее 10 литров керосина. Можно ли отлить из нее 6 литров керосина, используя девяти литровую и пятилитровую канистру?
Задача 65
В шести литровом ведре 4 литра парного молока, а в семи литровом — 6 литров. Как из шести литрового ведра вылить ровно 1 литр при помощи еще одной трехлитровой банки?
Задача 66
В кастрюле налито 8 литров супа. Есть также пустые 3-х и 5-тислитровая банки. Требуется отмерить 4 литра супа. Как это сделать, если суп нельзя проливать?
Задача 67
Миссис Брэйн решила порадовать Эрудита и приготовила ему квас. Эрудит сказал, что возьмет только 4 литра кваса ни больше ни меньше. У миссис Брэйн дома только 2 сосуда объемом 8 и 5 литров.Как миссис Брэйн с помощью двух сосудов объемом 8 и 5 литров налить Эрудиту ровно 4 литра кваса?
Задача 68
Есть 2 сосуда. Емкость одного 9 л другого 4л. Как с их помощью из бака набрать 6л воды? Воду можно сливать обратно в бак.
Задача 69
Для путешествия по морю необходим запас пресной воды. В плавании вода расходуется со скоростью 1 бочка в сутки. В некоторый момент времени запас воды на берегу составлял 8 бочек, и вода находилась в баке, заполненном до краев. На яхте имеется такой же бак, объемом 8 бочек, но пустой. На сколько дней можно планировать путешествие, если с собой нельзя брать лишнюю воду, а в распоряжении имеется еще две пустых емкости объемом 3 и 6 бочек и их можно использовать для переливания воды?
Задача 70
В бочке 20 литров вина. Сосед просит налить ему 5 литров а сам пришел с ведрами на 7 и 13 литров. Нет проблем – сказал хозяин. Как он поступил?

Источник
Проектная работа
«Задачи на переливание»
Работу выполнили
учащиеся 6 б класса
Васильев Валерий,
Хаертдинов Марсель
Руководитель
Кочкурова Л.Б.,
учитель математики
Содержание
1.Введение………………………………………………………………………………………… 3
2. Немного истории………………………………………………………………………………. 4
3. Типы задач на переливание, алгоритм их решения…………………………………… 5
4. Примеры задач на переливание, где участвуют два сосуда, воду наливают из водопроводного крана (реки), лишнюю воду выливают……………………………… 6
5. Примеры задач, в которых три сосуда и воду выливать нельзя……………………… 8
6. Литература…………………………………………………………………………………… 10
Цель проекта – реализация проектного замысла: изучить виды логических задач на переливание, алгоритмы их решения, учиться применять их на практике.
Результат – заранее продуманный проектный продукт: решение практических задач.
Актуальность и выбор темы связаны следующим фактором: мы активные участники дистанционных олимпиад по математике и заметили, что часто встречаются подобные задачи.
Введение
Практически ни один классический сборник, связанный с играми и развлечениями, не обходится без раздела «Дележи», причём заметное место в нём занимают задачи о переливании жидкостей из сосуда в сосуд. Задачи на переливание – это задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости. Простейший прием решения задач этого класса состоит в переборе возможных вариантов. Понятно, что такой метод решения не совсем удачный, в нем трудно выделить какой-либо общий подход к решению других подобных задач. Более систематический подход к решению задач “на переливание” заключается в использовании отдельных таблиц, в которые заносят количество жидкости в каждом из имеющихся сосудов. Задачи на переливание относят к логическим задачам, решение которых не только очень увлекательный, но и полезный способ времяпрепровождения, как для школьников, так и для взрослых.
Немного истории
Непросто определить, в каком старинном трактате впервые появились задачи на переливание жидкостей. Пожалуй, самая известная из них опубликована более семи веков назад. Познакомимся с ней. В одном средневековом сочинении, восходящим к середине 13-го столетия, предлагается такого рода задача: «Господин послал своего слугу в ближайший город купить 8 мер вина. Когда слуга, выполнив поручение, собирался домой, ему повстречался другой слуга, которого господин тоже послал за вином. «Сколько у тебя вина?» — спрашивает второй слуга. «8 мер», — отвечает тот. «Мне тоже нужно купить вина». «Ты уже ничего не получишь, так как в городе больше вина нет», — заявляет первый. Тогда второй слуга просит его поделиться с ним вином и показывает ему имеющиеся при нём два сосуда, один в 5, другой в 3 меры. Как произвести делёж при помощи этих трёх сосудов? (т. е. у каждого из слуг должно получиться ровно по 4 меры вина)».
 Одной из самых известных задач подобного рода является задача Симеона Дени Пуассона (1781 – 1840), знаменитого французского математика и физика. Именно с решением одной из сложных задач о переливаниях, связывают раскрытие математических способностей выдающегося французского математика С. Д. Пуассона. Говорят, что эта задача сыграла решающую роль в выборе профессии. Однажды, знакомый принес юному Пуассону несколько задач на переливание, разного уровня сложности. Пуассон решил их менее чем за час, и определил выбор своей будущей профессии – математик.
Одной из самых известных задач подобного рода является задача Симеона Дени Пуассона (1781 – 1840), знаменитого французского математика и физика. Именно с решением одной из сложных задач о переливаниях, связывают раскрытие математических способностей выдающегося французского математика С. Д. Пуассона. Говорят, что эта задача сыграла решающую роль в выборе профессии. Однажды, знакомый принес юному Пуассону несколько задач на переливание, разного уровня сложности. Пуассон решил их менее чем за час, и определил выбор своей будущей профессии – математик.
Типы задач на переливание, алгоритм их решения
Все задачи на переливание можно представить двумя типами:
«Водолей» – задачи, в которых необходимо получить некоторое количество жидкости с помощью нескольких пустых емкостей из бесконечного источника, из которого можно наливать жидкость, и в который ее можно выливать.
«Переливашка» – задачи, в которых необходимо разделить жидкость в большей емкости с помощью нескольких меньших по объему емкостей, жидкость можно только переливать из одной емкости в другую.
Первый тип задач кажется полегче, второй – сложнее.
В задачах на переливание разрешены следующие операции:
заполнение жидкостью одного сосуда до краев;
переливание жидкости в другой сосуд или выливание жидкости;
При решении таких задач необходимо учитывать следующие замечания:
разрешается наливать в сосуд ровно столько жидкости, сколько в нем помещается;
разрешается переливать всю жидкость из одного сосуда в другой, если она в него вся помещается;
разрешается отливать из одного сосуда в другой столько жидкости, сколько необходимо, чтобы второй сосуд стал полным.
Каждую задачу на переливание таким методом можно решать двумя способами:
а) начать переливания с большего сосуда;
б) начать переливания с меньшего сосуда.
Какой из способов более рационален (т.е. каким способом мы быстрее получим нужное количество жидкости) зависит от условий задачи. Изначально это определить нельзя.
При решении задач первого типа («Водолей») можно использовать такой алгоритм:
Наполнить большую емкость жидкостью из бесконечного источника.
Перелить из большей емкости в меньшую емкость.
Вылить жидкость из меньшей емкости.
Повторить действия 1-3 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
При решении задач второго типа («Переливашка») можно использовать следующий алгоритм:
Из большей емкости наполнить емкость промежуточного объема.
Перелить жидкость из промежуточной емкости в самую маленькую емкость.
Перелить жидкость из самой маленькой емкости в большую емкость.
Повторять действия 2-3 до тех пор, пока емкость промежуточного объема не станет пустой.
Если емкость промежуточного объема опустела, то повторить действия 1-5 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
Примеры задач на переливание, где участвуют два сосуда, воду наливают из водопроводного крана (реки), лишнюю воду выливают
1. Как, имея два ведра: емкостью 5 и 9 литров, набрать из реки ровно 3 литра воды?
Решение:
1шаг – набираем 9л и переливаем в 5литровую, остается 4л
2шаг – 5литровую выливаем и переливаем туда эти 4л
3 шаг – теперь снова набираем 9л и доливаем из нее в 5литровую, тогда останется 8л
4 шаг – 5литровую выливаем и отливаем 5л от 8л, останется 3л
Задача решена. В 9-литровом сосуде получили ровно 3л.
2. Как с помощью 2-литровой и 5-литровой банок отмерить ровно 1 литр?
Решение: Задача решена. В 5-литровом сосуде получили ровно 1л.
3. Есть два кувшина емкостью 5 л и 9 л. Нужно набрать из источника 7 л воды, если можно пользоваться только кувшинами.
а)Решим задачу, наполнив первым действием 5-литровый кувшин.
б)Решим задачу иначе. Наполним первым действием 9-литровый кувшин.
Задача решена. В 9-литровом кувшине получили ровно 7л.
4. Для разведения картофельного пюре быстрого приготовления “Зеленый великан” требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?
Решение :
Задача решена. В 5-литровом сосуде получили ровно 1л.
5. Для марш-броска по пустыне путешественнику необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, выдают только 5-литровые фляги, а также имеются 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?
Решение :
Задача решена. Во фляге получили ровно 4л.
6. Имеются два сосуда вместимостью 3л и 5л. Как с помощью этих сосудов налить из водопроводного крана 4 л воды?
Решение :
3л
3
2
2
3
5л
5
2
2
5
4
Задача решена. В 5-литровом сосуде останется ровно 4л.
7. Имеются два сосуда вместимостью 8л и 5л. Как с помощью этих сосудов налить из водопроводного крана 7л воды?
8л
5
5
8
2
2
7
5 л
5
5
2
2
5
Решение :
Задача решена. В 8-литровом сосуде получили ровно 7л.
8. Как, имея два ведра емкостью 4л и 9л, налить из водопроводного крана 6л воды?
9л
9
5
5
1
1
9
6
4л
4
4
1
1
4
Решение :
Задача решена. В 9-литровом ведре останется ровно 6л.
9. Как, имея лишь два сосуда вместимостью 5л и 7л, налить из водопроводного крана 6л воды?
7л
7
2
2
7
4
4
7
6
5л
5
2
2
5
4
6
5
Решение :
Задача решена. В 7-литровом сосуде останется ровно 6л.
10. Имеются два сосуда вместимостью 17л и 5л. Как с помощью этих сосудов налить из водопроводного крана 13л воды?
Решение :
17 л
5
5
10
10
15
15
17
3
3
8
8
13
5 л
5
5
5
5
3
3
5
5
Задача решена. В 17-литровом сосуде останется ровно 13л.
Примеры задач, в которых три сосуда и воду выливать нельзя
Воду берут не из водопроводного крана. В таких задачах вода уже есть в каком-то сосуде, например, в самом большом. А маленькими ёмкостями мы будем переливать воду. Выливать воду нельзя. Если необходимо освободить сосуд, то лишнюю воду выливают в другой сосуд. Обычно больший сосуд – это хранилище, откуда берут воду и в него сливают лишнюю. Таблица может быть составлена на три сосуда, а можно обойтись и таблицей на два сосуда.
1. Бидон ёмкостью 10 л наполнен молоком. Требуется перелить из этого бидона 5 л в семилитровый бидон, используя при этом ещё один бидон, вмещающий 3 л. Как это сделать?
Запись решения отражает только два сосуда. В решении покажем только два бидона 5л и 3 л. Выливать молоко будем обратно в 10-литровый бидон.
1 действие. Из 10-литрового бидона нальем 3-литвовый бидон.
7 л
3
3
6
6
7
2
2
5
3 л
3
3
3
2
2
3
Запись решения отражает все три сосуда. В решении покажем как изменялось количество молока во всех трех бидонах. Т.е. добавляем еще строку выше для 10-литрового бидона, чтобы следить за количеством молока в нем. Это не сложно: надо следить за тем, чтобы общее количество молока все время было 10 литров.
1 действие. Из 10-литрового бидона нальем 3-литвовый бидон.
10 л
7
7
4
4
1
1
8
8
5
5
7 л
3
3
6
6
7
2
2
5
3 л
3
3
3
2
2
3
Второй способ решения этой задачи. Можно начать с заполнения 7-литрового бидона. Решение получилось короче на два переливания.
10 л
3
3
6
6
9
9
2
2
7 л
7
4
4
1
1
7
5
3 л
3
3
1
1
3
2. Двое должны разделить поровну 8 вёдер кваса, находящегося в большом бочонке. Но у них есть ещё только два пустых бочонка, в один из которых входит 5 вёдер, а в другой – 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками?
Решение:
Разделить квас пополам, т.е. надо получить 4 ведра. Начнем с заполнения 3-ведерного бочонка. Из 8-ведерного будем наполнять бочонки и сливать туда квас, когда нам надо будет освободить сосуд.
8 – вед
5
5
2
2
7
7
4
4
5 – вед
3
3
5
1
1
4
3х- вед
3
3
1
1
3
Задача решена. В 5-ведерном бочонке получилось 4 ведра кваса.
Еще 4 ведра в 8-ведерном бочонке. 3. В первый сосуд входит 8 л и он наполнен водой. Имеются еще два пустых сосуда ёмкостью 5л и 3л. Как с помощью этих сосудов отмерить ровно 1 л?
Решение:
8 л
8
3
3
5
5
2
2
5 л
5
2
3
3
5
3 л
3
3
3
1
Задача решена.В 3-литровом сосуде получился 1 л воды.
4. В первый сосуд входит 12 л и он наполнен водой. Имеются еще два пустых сосуда ёмкостью 5л и 8л. Как разделить воду на две равные части?
Решение:
12 л
12
4
4
9
9
1
1
6
8 л
8
3
3
8
6
6
5 л
5
3
3
5
Задача решена.
Литература
Ф.Ф.Нагибин, Е.С.Канин . Математическая шкатулка М.: Просвещение, 1988
Я.И.Перельман. Занимательная геометрия М.: ГИФМЛ, 1959
В.Н.Русанов. Математические олимпиады младших школьников М.:Просвещение, 1990
Е.П.Коляда. Развитие логического и алгоритмического мышления учащихся //Информатика и образование. 1996. N1.
И.Ф.Шарыгин. Математический винегрет М., АГЕНТСТВО “ОРИОН”, 1991
В век новых информационных технологий мы много времени тратим на бессмысленные игры на компьютере. А не лучше ли заняться решением разного типа логических задач, решения которых не требуют сложных математических вычислений?
Ведь задачи на логику развивают в человеке догадливость, сообразительность и интеллект. А мышление – высшая ступень познания человеком действительности.
Логические или нечисловые задачи составляют обширный класс нестандартных задач. К классу логических задач относятся и задачи на переливания. Задачи на переливание – это не привычные всем со школы математические задачи.
В данной работе рассматриваются виды задач на переливание, алгоритмы их решения, приводится решение некоторых из них. При решении задач авторы проявили исключительную самостоятельность. Процесс решения задач на переливание был очень увлекательным, но и крайне полезным способом времяпрепровождения и хорошим способом развития умственных способностей авторов работы. Данная работа была представлена на школьной НПК, апробирована в виде презентации и получила отличную оценку среди работ шестиклассников.
Источник
