Уравнение лапласа в сосуде

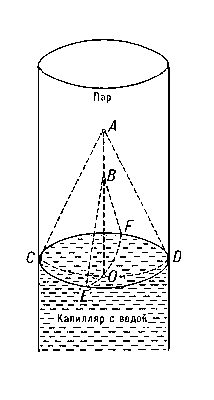
Поверхность жидкости у стенки сосуда искривляется, образуя мениск.

Искривление поверхностной пленки в жидкости создает некое дополнительное давление, которое имеет очень большое значение в капиллярных явлениях или в пузырьковых системах. В общем виде данное давление вычисляют по формуле, выведенной П. С. Лапласом.

Мениск жидкости

Направления сил поверхностного натяжения в этих пределах, при условии, что первоначальный уровень поверхности жидкости горизонтален, можно представить следующим образом:

Как видим, на частицу жидкости А А А действуют три силы поверхностного натяжения. Поскольку α 1 α_1 α1​ (сила поверхностного натяжения на границе жидкость – твёрдого тело) в общем не равна α 3 α_3 α3​ (на границе пар – твердое тело), то жидкость в области А А А подниматься или опускаться в зависимости от того, какая из указанных сил больше. При α 1 > α 3 α_1 > α_3 α1​>α3​ образуется вогнутый мениск:

а при α 3 > α 1 α_3 > α_1 α3​>α1​ – выпуклый

На краю мениска сила α 2 α_2 α2​ становится касательной к поверхности жидкости и образует со стенкой сосуда некоторый краевой угол θ θ θ. Вертикальная составляющая этой силы α 2 c o s θ α_2 cos θ α2​cosθ обуславливает установление равновесия сил в точке А А А. Равновесие наступает, когда обеспечиваются равенство:

α 3 = α 1 + α 2 c o s θ α_3 = α_1 + α_2 cos θ α3​=α1​+α2​cosθ

для вогнутого мениска и

α 1 = α 3 + α 2 c o s θ α_1 = α_3 + α_2 cos θ α1​=α3​+α2​cosθ

для выпуклого мениска.

Краевой угол θ θ θ измеряют всегда со стороны жидкости, поэтому для вогнутого мениска он острый, а для выпуклого – тупой.

Форма мениска жидкости вблизи стенок сосуда тесно связана с явлением смачивания (см. соотв. статью «Смачивание»). Его суть объясняется взаимодействиями молекул жидкости с молекулами стенок сосуда. Жидкость, которая смачивает стенки (например, вода – стекло) образует вогнутый мениск, а жидкость, которая не смачивает (например, ртуть – стекло), – выпуклый мениск. Эти явления играют существенную роль в капиллярах.

Давление сферической пленки

Всякая поверхностная пленка жидкости под действием сил поверхностного натяжения пытается сократиться до минимальной площади. В частности, если поверхностная пленка искривлена, то она пытается стать плоской. Однако, пытаясь стать плоской, выпуклая пленка увеличивает давление на жидкость, а вогнутая – уменьшает его:

Иначе говоря, кривая поверхностная пленка создает в жидкости дополнительное давление к давлению на нее плоской поверхностной пленки.

Найдем значение дополнительного давления под кривой поверхностью. Пусть жидкость ограничено сферической поверхностью радиусом R R R. Под действием дополнительного давления поверхностной пленки жидкость сжимается, поэтому радиус сферы уменьшается на d R dR dR:

При этом выполняется некоторая работа d A dA dA, которую можно вычислить по давлению p α pα pα поверхностной пленки и изменению объема d V dV dV жидкости:

d A = p α d V dA = pα dV dA=pαdV

или по коэффициенту поверхностного натяжения α α α и сокращением поверхности d S dS dS жидкости:

d A = α d S dA = α dS dA=αdS.

Приравняв правые части формул, получим:

p α d V = α d S pα dV = α dS pαdV=αdS.

Если выразить дифференциалы объема и поверхности жидкости через изменение радиуса указанной сферы:

d V = d ( 4 3 π R 3 ) = 4 π R 2 d R dV=dleft( frac{4}{3}pi {{R}^{3}} right)=4pi {{R}^{2}}dR dV=d(34​πR3)=4πR2dR

d S = d ( 4 π R 2 ) = 8 π R d R dS=dleft( 4pi {{R}^{2}} right)=8pi RdR dS=d(4πR2)=8πRdR

то равенство будет иметь вид:

p α ⋅ 4 π R 2 d R = α ⋅ 8 π R d R {{p}_{alpha }}cdot 4pi {{R}^{2}}dR=alpha cdot 8pi RdR pα​⋅4πR2dR=α⋅8πRdR

Откуда:

p α = 2 α R {{p}_{alpha }}=frac{2alpha }{R} pα​=R2α​

Таково дополнительное давление на жидкость сферической поверхностной пленки. В случае вогнутой сферической поверхности жидкости это давление будет отрицательным.

Давление пленки в общем виде

В общем виде, когда поверхность жидкости является поверхностью двоякой кривизны, дополнительное давление поверхностной пленки определяют по формуле, выведенной французским ученым П. С. Лапласом в 1806 г.:

p α = α ( 1 R 1 + 1 R 2 ) {{p}_{alpha }}=alpha left( frac{1}{{{R}_{1}}}+frac{1}{{{R}_{2}}} right) pα​=α(R1​1​+R2​1​)

где R 1 R_1 R1​ и R 2 R_2 R2​ – радиусы кривизны сечений поверхности жидкости. При R 1 = R 2 R_1 = R_2 R1​=R2​ в случае сферической поверхности по формуле Лапласа получают выражение, уже полученное нами выше – p α = 2 α / R pα=2α/R pα=2α/R.

Формула Лапласа свидетельствует о том, что дополнительное давление кривой поверхностной пленки прямо пропорционально коэффициенту поверхностного натяжения и обратно пропорционально радиусу ее кривизны.

Последняя зависимость хорошо наблюдается на таком опыте. Если с помощью стеклянного тройника, продленного двумя резиновыми трубками, выдуть два мыльных пузыря разного размера, а затем отверстие тройника закрыть, то больший пузырь начнет увеличиваться, а меньший – уменьшаться:

В меньшем пузырьке воздух будет находиться под большим лапласовским давлением, поэтому он перейдет в больший пузырь.

В очень малых пузырьках воздуха или пара в воде лапласовское давление становится значительным. Например, в пузырьке воздуха радиусом 10-9 м в воде лапласовское давление составит:

p α = 2 ⋅ 75 ⋅ 10 − 3 10 − 9 = 15 ⋅ 10 7 {{p}_{alpha }}=frac{2cdot 75cdot {{10}^{-3}}}{{{10}^{-9}}}=15cdot {{10}^{7}} pα​=10−92⋅75⋅10−3​=15⋅107 (Па)

Явление образования пузырьков в жидкости называется кавитацией. Она возникает в быстрых потоках жидкости в трубах, когда работают гребные винты кораблей, когда струя пара попадает в воду и тому подобное. Среда кавитационных пузырьков с огромным давлением в них является жесткой средой. Она может вызвать разрушение гребных винтов кораблей, лопастей гидротурбин и других гидротехнических устройств.

Тест по теме «Формула Лапласа»

Источник

Течение крови имеет следующие особенности:

1.В артериальной части системы кровообращения течение пульсирующее.

2.Сосуды радиально и продольно растяжимы, разветвлены и изогнуты.

3.В крупных сосудах может возникать турбулентное течение.

Сердечный насос, крупные артерии и вены образуют систему макроциркуляции, главная функциональная цель которой – обеспечить движение и транспорт крови. Система микроциркуляции состоит из артериол, венул, капилляров и артериовенозных анастомозов. Задача этой системы – распределить сердечный выброс между различными органами в соответствии с их потребностями.

1. Амортизирующие сосуды (аорта, легочная артерия и прилегающие к ним участки больших артерий). Выраженные эластические свойства таких сосудов обеспечивают амортизацию (сглаживание) периодических систолических волн кровотока.

2. Резистивные сосуды (в основном мелкие артерии и артериолы) оказывают наибольшее сопротивление кровотоку. Изменения степени сокращения мышечных волокон этих сосудов приводят к изменениям их диаметра и, следовательно, гидродинамического сопротивления. Сокращение гладких мышц этих сосудов является основным механизмом регуляции объемной скорости кровотока в различных сосудистых областях, а также распределения сердечного выброса по разным органам.

3. Сосуды-сфинктеры (последние отделы артериол)определяют в основном площадь обменной поверхности капилляров, изменяя число капилляров, функционирующих в каждый определенный момент.

4. Обменные сосуды (в основном капилляры) обеспечивают такие важнейшие процессы как диффузия и фильтрация.

5. Емкостные сосуды (главным образом вены) благодаря своей высокой растяжимости способны вмещать или выбрасовать большие объемы крови без существенного влияния на другие параметры кровотока. В связи с этим могут играть роль резервуаров крови.

6. Шунтирующие сосуды (артериовенозные анастомозы) осуществляют прямые связи между мелкими артериями и венами в обход капиллярного ложа. Присутствуют не во всех тканях.

Стенки всех артерий и вен имеют сходное строение и делится на три слоя: внутреннюю, среднюю и наружную оболочки.

Коллаген- белок с высокой прочностью на разрыв и относительно малой растяжимостью. Форма волокон коллагена в стенке сосуда напоминает серпантин, и возможно некоторое растяжение стенки без натяжения волокон. Коллогеновые волокна вносят основной вклад в жесткость стенки и предохраняют ее от разрушения. Эластин – белок, обладающий большой растяжимостью, его упругость важна для смягчения импульсов давления, возникающих при сокращениях сердца. Веретенообразные гладкомышечные клетки электрически соединены друг с другом и механически связаны с эластическими и коллагеновыми волокнами. Функция – создавать активное напряжение сосудистой стенки и изменять величину просвета сосудов в зависимости от физиологических потребностей.

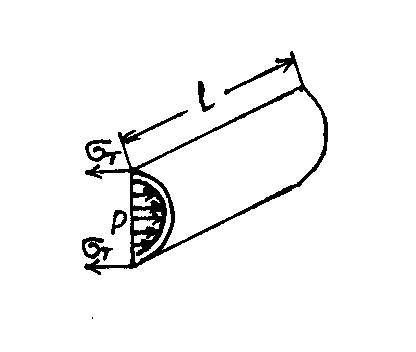
Надежность капилляра: малый d, толщина стенки.

З акон Лапласа: зависимость перепада капиллярного гидростатического давления p на поверхности раздела двух фаз от межфазного поверхностного натяжения σ: ΔP=P1- P2= εσ, где P1 – давление с вогнутой стороны поверхности, P2 – с выпуклой стороны, R1, R2 – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности в данной точке, R1 – стремится к 0, R2 – стремится к бесконечности: Рτ= σ (1/R1+ 1/ R2). σ = РτR2/hR, F = P2Rl, F= σ2hl, где 2 и l сокращаются в этих уравнениях и получается, что РR = σh, а отсюда следует, что σ = РR/h – это есть уравнение Ламе, σт – тангенциальные напряжения в стенке сосуда.(уравнение деформации сосудов)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Источник

В математике и физике уравнение Лапласа – это уравнение в частных производных второго порядка, названное в честь Пьера-Симона Лапласа, который первым изучил его свойства. Это часто записывается как

где – оператор Лапласа , – оператор дивергенции (также обозначается как “div”), является оператором градиента (также обозначается как “град”) и является дважды дифференцируемой вещественной функцией. Следовательно, оператор Лапласа отображает скалярную функцию на другую скалярную функцию.

Если правая часть задана как заданная функция , мы имеем

Это называется уравнением Пуассона , обобщением уравнения Лапласа. Уравнение Лапласа и уравнение Пуассона являются простейшими примерами эллиптических уравнений в частных производных . Уравнение Лапласа также является частным случаем уравнения Гельмгольца .

Общая теория решений уравнения Лапласа известна как теория потенциала . Решения уравнения Лапласа – это гармонические функции , которые важны во многих областях физики, особенно в электростатике, гравитации и гидродинамике . При исследовании теплопроводности уравнение Лапласа является уравнением стационарной теплопроводности . В общем, уравнение Лапласа описывает ситуации равновесия или те, которые не зависят явно от времени.

Формы в разных системах координат

В прямоугольных координатах ,

В цилиндрических координатах ,

В сферических координатах , используя соглашение,

В более общем смысле, в криволинейных координатах ,

или же

Граничные условия

Уравнение Лапласа на кольце (внутренний радиус r = 2 и внешний радиус R = 4) с граничными условиями Дирихле u ( r = 2) = 0 и u ( R = 4) = 4 sin (5 θ )

Задача Дирихле для уравнения Лапласа состоит в нахождении решения φ в некоторой области D такого, что φ на границе D равен некоторой заданной функции. Поскольку оператор Лапласа появляется в уравнении теплопроводности , одна физическая интерпретация этой проблемы заключается в следующем: зафиксировать температуру на границе области в соответствии с заданной спецификацией граничного условия. Позвольте теплу течь до тех пор, пока не будет достигнуто стационарное состояние, при котором температура в каждой точке домена больше не будет меняться. Распределение температуры внутри будет тогда дано решением соответствующей задачи Дирихле.

В граничных условиях Неймана для уравнения Лапласа указать не функцию ф себя на границе D , но ее нормальную производную . Физически это соответствует построению потенциала для векторного поля, действие которого , как известно , на границе D только. Для примера уравнения теплопроводности это означает задание теплового потока через границу. В частности, на адиабатической границе нормальная производная φ равна нулю.

Решения уравнения Лапласа называются гармоническими функциями ; все они аналитичны в той области, где выполняется уравнение. Если любые две функции являются решениями уравнения Лапласа (или любого линейного однородного дифференциального уравнения), их сумма (или любая линейная комбинация) также является решением. Это свойство, называемое принципом суперпозиции , очень полезно. Например, решения сложных проблем могут быть построены путем суммирования простых решений.

В двух измерениях

Уравнение Лапласа с двумя независимыми переменными в прямоугольных координатах имеет вид

Аналитические функции

Действительная и мнимая части комплексной аналитической функции удовлетворяют уравнению Лапласа. То есть, если z = x + iy , и если

то необходимое условие аналитичности f ( z ) состоит в том, чтобы u и v были дифференцируемыми и чтобы выполнялись уравнения Коши – Римана :

где u x – первая частная производная u по x . Следует, что

Следовательно, u удовлетворяет уравнению Лапласа. Аналогичный расчет показывает, что v также удовлетворяет уравнению Лапласа. И наоборот, если дана гармоническая функция, это действительная часть аналитической функции f ( z ) (по крайней мере, локально). Если пробная форма

то уравнения Коши – Римана будут выполнены, если положить

Это соотношение не определяет ψ , а только его приращения:

Уравнение Лапласа для φ означает, что выполняется условие интегрируемости для ψ :

и, таким образом, ψ можно определить линейным интегралом. Из условия интегрируемости и теоремы Стокса следует, что значение линейного интеграла, соединяющего две точки, не зависит от пути. Полученная пара решений уравнения Лапласа называется сопряженными гармоническими функциями . Эта конструкция действительна только локально или при условии, что путь не огибает особенность. Например, если r и θ полярные координаты и

то соответствующая аналитическая функция

Однако угол θ однозначен только в области, не охватывающей начало координат.

Тесная связь между уравнением Лапласа и аналитическими функциями подразумевает, что любое решение уравнения Лапласа имеет производные всех порядков и может быть разложено в ряд по степеням, по крайней мере, внутри круга, не содержащего сингулярности. Это резко контрастирует с решениями волнового уравнения , которые обычно имеют меньшую регулярность.

Между степенными рядами и рядами Фурье существует тесная связь . Если мы разложим функцию f в ряд по степеням внутри круга радиуса R , это означает, что

с подходящим образом определенными коэффициентами, действительная и мнимая части которых задаются формулой

Следовательно

который является рядом Фурье для f . Эти тригонометрические функции могут быть расширены с помощью формул для нескольких углов .

Поток жидкости

Пусть величины u и v являются горизонтальной и вертикальной составляющими поля скорости стационарного несжимаемого безвихревого потока в двух измерениях. Условие непрерывности несжимаемого потока состоит в том, что

и условием безвихревого потока является то, что

Если мы определим дифференциал функции ψ формулой

тогда условие непрерывности является условием интегрируемости этого дифференциала: результирующая функция называется функцией тока, поскольку она постоянна вдоль линий потока . Первые производные от ψ даются формулами

а из условия безвихревости следует, что ψ удовлетворяет уравнению Лапласа. Гармоническая функция φ , сопряженная с ψ , называется потенциалом скорости . Из уравнений Коши – Римана следует, что

Таким образом, каждая аналитическая функция соответствует установившемуся несжимаемому, безвихревому, невязкому потоку жидкости на плоскости. Действительная часть – это потенциал скорости, а мнимая часть – функция тока.

Электростатика

Согласно уравнениям Максвелла электрическое поле ( u , v ) в двух пространственных измерениях, которое не зависит от времени, удовлетворяет

и

где ρ – плотность заряда. Первое уравнение Максвелла является условием интегрируемости дифференциала

поэтому электрический потенциал φ может быть построен так, чтобы удовлетворять

Из второго уравнения Максвелла тогда следует, что

что является уравнением Пуассона . Уравнение Лапласа может использоваться в трехмерных задачах электростатики и потока жидкости так же, как в двух измерениях.

В трех измерениях

Фундаментальное решение

Фундаментальное решение уравнения Лапласа удовлетворяет

где дельта-функция Дирака δ обозначает единичный источник, сосредоточенный в точке ( x ′, y ′, z ′) . Ни одна функция не обладает этим свойством: на самом деле это скорее распределение , чем функция; но его можно рассматривать как предел функций, интегралы которых по пространству равны единице, а носитель (область, где функция отлична от нуля) сжимается до точки (см. слабое решение ). Обычно для этого уравнения используют другое соглашение о знаках, чем при определении фундаментальных решений. Этот выбор знака часто удобен для работы, потому что −Δ – положительный оператор . Таким образом, из определения фундаментального решения следует, что если лапласиан функции u проинтегрирован по любому объему, охватывающему точку источника, то

Уравнение Лапласа не изменяется при повороте координат, и, следовательно, мы можем ожидать, что фундаментальное решение может быть получено среди решений, которые зависят только от расстояния r от точки источника. Если мы выберем в качестве объема шар радиуса a вокруг точки источника, то из теоремы Гаусса о расходимости следует, что

Следует, что

на сфере радиуса r , центрированной в точке источника, и, следовательно,

Обратите внимание, что с противоположным соглашением о знаках (используемым в физике ), это потенциал, генерируемый точечной частицей , для силы закона обратных квадратов , возникающей при решении уравнения Пуассона . Аналогичный аргумент показывает, что в двух измерениях

где log ( r ) обозначает натуральный логарифм . Обратите внимание, что с противоположным соглашением о знаках это потенциал, генерируемый точечным стоком (см. Точечная частица ), который является решением уравнений Эйлера в двумерном потоке несжимаемой жидкости .

Функция Грина

А функция Грина является фундаментальным решением , которое также удовлетворяет подходящее условие на границе S объемной V . Например,

может удовлетворить

Теперь, если u – любое решение уравнения Пуассона в V :

и u принимает граничные значения g на S , тогда мы можем применить тождество Грина (следствие теоремы о расходимости), которое утверждает, что

Обозначения U п и G п обозначают нормальные производные на S . С учетом условий, которым удовлетворяют u и G , этот результат упрощается до

Таким образом, функция Грина описывает влияние в ( x ′, y ′, z ′) данных f и g . Для случая внутренней части сферы радиуса a функция Грина может быть получена посредством отражения ( Sommerfeld 1949 ): точка источника P на расстоянии ρ от центра сферы отражается вдоль своей радиальной линии до точки точка P ‘ , находящаяся на расстоянии

Обратите внимание, что если P находится внутри сферы, то P ‘ будет вне сферы. Тогда функция Грина определяется выражением

где R обозначает расстояние до точки P источника, а R ′ обозначает расстояние до отраженной точки P ′. Следствием этого выражения для функции Грина является интегральная формула Пуассона . Пусть ρ , θ и φ – сферические координаты точки P источника . Здесь θ обозначает угол с вертикальной осью, что противоречит обычным американским математическим обозначениям, но соответствует стандартной европейской и физической практике. Тогда решение уравнения Лапласа с граничными значениями Дирихле g внутри сферы имеет вид

( Захманоглов, 1986 , с. 228).

куда

– косинус угла между ( θ , φ ) и ( θ ′, φ ′) . Простое следствие этой формулы состоит в том, что если u – гармоническая функция, то значение u в центре сферы является средним значением его значений на сфере. Это свойство среднего значения сразу означает, что непостоянная гармоническая функция не может принимать максимальное значение во внутренней точке.

Сферические гармоники Лапласа

Действительные (лапласовские) сферические гармоники Y ℓ m для ℓ = 0,…, 4 (сверху вниз) и m = 0,…, ℓ (слева направо). Зональные, секторальные и тессеральные гармоники изображены вдоль самого левого столбца, главной диагонали и в других местах соответственно. (Гармоники отрицательного порядка будут показаны повернутыми вокруг оси z относительно гармоник положительного порядка.)

Уравнение Лапласа в сферических координатах :

Рассмотрим задачу поиска решений вида f ( r , θ , φ ) = R ( r ) Y ( θ , φ ) . При разделении переменных , два дифференциальных уравнений приводят налагая уравнению Лапласа:

Второе уравнение можно упростить, если предположить, что Y имеет вид Y ( θ , φ ) = Θ ( θ ) Φ ( φ ) . Повторное применение разделения переменных ко второму уравнению уступает место паре дифференциальных уравнений

для некоторого числа m . Априори m – комплексная константа, но поскольку Φ должна быть периодической функцией , период которой делит 2 π , m обязательно является целым числом, а Φ – линейной комбинацией комплексных экспонент e ± imφ . Функция решения Y ( θ , φ ) регулярна в полюсах сферы, где θ = 0, π . Наложение этой регулярности в решение Θ второго уравнения в граничных точках области представляет собой задачу Штурма – Лиувилля , вынуждающую параметр λ иметь вид λ = ℓ ( ℓ + 1) для некоторого неотрицательного целого числа с ℓ ≥ | м | ; это также объясняется ниже с точки зрения орбитального углового момента . Кроме того, замена переменных t = cos θ преобразует это уравнение в уравнение Лежандра , решение которого кратно соответствующему многочлену Лежандра P ℓ m (cos θ ) . Наконец, уравнение для R имеет решения вида R ( r ) = A r ℓ + B r – ℓ – 1 ; Требование, чтобы решение было регулярным по всему R 3, вынуждает B = 0 .

Здесь предполагалось, что решение имеет специальный вид Y ( θ , φ ) = Θ ( θ ) Φ ( φ ) . Для данного значения ℓ существует 2 ℓ + 1 независимых решений этой формы, по одному для каждого целого числа m с – ℓ ≤ m ≤ ℓ . Эти угловые решения являются продуктом тригонометрических функций , представленных здесь в виде комплексной экспоненты , и связанных полиномов Лежандра:

которые выполняют

Здесь Y ℓ м называется сферической гармонической функцией степени л и порядка т , Р л м приведены связанный полином Лежандра , Н является константой нормировки, а θ и ф представляет кошироту и долготы, соответственно. В частности, широта θ или полярный угол варьируется от 0 на Северном полюсе, до π / 2 на экваторе, до π на Южном полюсе, а долгота φ или азимут может принимать все значения с 0 ≤ φ <2 π . При фиксированном целочисленном л , каждое решение Y ( θ , φ ) проблемы собственных значений

является линейной комбинацией из Y л м . Фактически, для любого такого решения r ℓ Y ( θ , φ ) является выражением в сферических координатах однородного многочлена, который является гармоническим (см. Ниже ), и поэтому подсчет измерений показывает, что существует 2 ℓ + 1 линейно независимых таких многочленов. .

Общее решение уравнения Лапласа в шаре с центром в начале координат представляет собой линейную комбинацию функций сферической гармоники, умноженных на соответствующий масштабный коэффициент r ℓ ,

где е л м константа и коэффициенты г л Y л м известны как твердые гармоники . Такое расширение справедливо в шаре

Для выбираются сплошные гармоники с отрицательными степенями . В этом случае необходимо расширить решение известных областей в ряду Лорана (около ), а не в ряду Тейлора (около ), чтобы сопоставить члены и найти .

Электростатика

Позвольте быть электрическому полю, быть плотностью электрического заряда и быть диэлектрической проницаемостью свободного пространства. Тогда закон Гаусса для электричества (первое уравнение Максвелла) в дифференциальной форме утверждает

Теперь электрическое поле можно выразить как отрицательный градиент электрического потенциала ,

если поле безвихревое, . Неповоротливость также известна как электростатическое состояние.

Подставляя это соотношение в закон Гаусса, мы получаем уравнение Пуассона для электричества:

В частном случае области, свободной от источника , уравнение Пуассона сводится к уравнению Лапласа для электрического потенциала.

Если электростатический потенциал задан на границе области , то он определяется однозначно. Если он окружен проводящим материалом с заданной плотностью заряда , и если известен общий заряд , то он также уникален.

Потенциал, который не удовлетворяет уравнению Лапласа вместе с граничным условием, является недопустимым электростатическим потенциалом.

Гравитация

Позвольте быть гравитационное поле, плотность массы и гравитационная постоянная. Тогда закон Гаусса для гравитации в дифференциальной форме имеет вид

Гравитационное поле консервативно и поэтому может быть выражено как отрицательный градиент гравитационного потенциала:

Используя дифференциальную форму закона всемирного тяготения Гаусса, имеем

что является уравнением Пуассона для гравитационных полей.

В пустом пространстве, и у нас есть

что является уравнением Лапласа для гравитационных полей.

В метрике Шварцшильда

С. Персидес решил уравнение Лапласа в пространстве-времени Шварцшильда на гиперповерхностях постоянной t . Используя канонические переменные r , θ , φ, решение имеет вид

где Y l ( θ , φ ) – сферическая гармоническая функция , а

Здесь P l и Q l – функции Лежандра первого и второго рода соответственно, а r s – радиус Шварцшильда . Параметр l – произвольное неотрицательное целое число.

Смотрите также

• 6-сферные координаты , система координат, при которой уравнение Лапласа становится R- разделимым
• Уравнение Гельмгольца , общий случай уравнения Лапласа.
• Сферическая гармоника
• Квадратурные области
• Возможная теория
• Потенциальный поток
• Преобразование Бейтмана
• Теорема Ирншоу использует уравнение Лапласа, чтобы показать, что стабильная статическая ферромагнитная подвеска невозможна.
• Векторный лапласиан
• Фундаментальное решение

Примечания

1. ^ Символ дельты, Δ, также обычно используется для представления конечного изменения некоторой величины, например, . Его использование для представления лапласиана не следует путать с этим использованием.

Рекомендации

дальнейшее чтение

• Эванс, LC (1998). Уравнения с частными производными . Провиденс: Американское математическое общество. ISBN 978-0-8218-0772-9 .
• Петровский И.Г. (1967). Уравнения с частными производными . Филадельфия: У. Б. Сондерс.
• Полянин, АД (2002). Справочник по линейным дифференциальным уравнениям с частными производными для инженеров и ученых . Бока-Ратон: Chapman & Hall / CRC Press. ISBN 978-1-58488-299-2 .
• Зоммерфельд, А. (1949). Уравнения с частными производными в физике . Нью-Йорк: Academic Press.
• Захманоглу, EC (1986). Введение в дифференциальные уравнения с частными производными с приложениями . Нью-Йорк: Дувр.

внешняя ссылка

• “Уравнение Лапласа” , Математическая энциклопедия , EMS Press , 2001 [1994]
• Уравнение Лапласа (частные решения и краевые задачи) в EqWorld: The World of Mathematical Equations.
• Пример начально-краевой задачи с использованием уравнения Лапласа с сайта exampleproblems.com.
• Вайсштейн, Эрик В. “Уравнение Лапласа” . MathWorld .
• Узнайте, как можно численно решить краевые задачи, описываемые уравнением Лапласа, методом граничных элементов.

Источник