Уровень в сосуде не изменится
6. Механика (изменение физических величин в процессах)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Деревянный шарик плавает в воде. Как изменятся сила Архимеда и высота части шара, выступающей над поверхностью жидкости, если шар перенести в сосуд с маслом?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Высота части шара, выступающей над поверхностью воды}\
hline
&\
hline
end{array}]
1) Так как шар плавает в жидкости, то сила Архимеда уравновешивает силу тяжести, а так как сила тяжести не изменилась, значит, сила Архимеда не изменилась. Ответ — 3
2) Сила Архимеда находится по формуле: (F_text{арх}=rho g V_text{т}), где (rho) — плотность жидкости, (V_text{т}) — объем тела погруженного в жидкость. Так как (F_text{арх}) не изменилась, (rho) уменьшилась, а (g) постояна, то (V_text{т}) увеличится, следовательно, высота части шара, выступающей над жидкостью уменьшится. Ответ — 2
Ответ: 32
Деревянный шарик плавает в воде. Как изменятся давление на дно сосуда и сила тяжести, если шар перенести в сосуд с маслом? (Сосуды одинаковые, уровень жидкости до погружения шарика одинаковый.)
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила тяжести}&text{Сила давления на дно}\
hline
&\
hline
end{array}]
1) Сила тяжести находится по формуле: (F=mg), так как масса шарика не меняется, то и сила тяжести не изменяется. Ответ — 3
2) Сила давления находится по формуле: ( displaystyle F=rho g h S), где (rho) — плотность жидкости, (h) — высота столба жидкости (S) — площадь дна, или эту формулу можно заменить на равносильную [F=m_1g] (m_1) – масса жидкости, так как плотность воды больше плотности масла, то масса жидкости уменьшилась, значит, сила давления уменьшилась. Ответ — 2
Ответ: 32
На поверхности воды плавает небольшая льдинка. Как изменятся сила Архимеда, действующая на льдинку, и давление на дно сосуда, если часть льдинки растает?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Давление на дно сосуда}\
hline
&\
hline
end{array}]
1) Так как часть льда растает, то (m_text{л}) уменьшится. Так как лед плавает, то сила архимеда уравновешивает силу тяжести. [F_text{а}=m_text{л}g] А так как масса льда уменьшилась, то и сила Архимеда уменьшилась. Ответ — 2
2) Так как лед плавает, то [F_text{а}=m_text{л}g] или (m_text{л}=rho_text{в}V_text{т}), где (rho_text{в}) — плотность воды, а (V_text{т}) — объем погруженной части тела.
Выразим объем погруженной части [V_text{т}=frac{m_text{л}}{rho_text{в}} quad (1)] Объем полученной воды равен [V_text{в}=frac{m_text{л}}{rho_text{в}} quad (2)] Из (1) и (2) можно сделать вывод, что ( V_ text{в}=V_text{т}), а значит объем погруженной в воду части льда будет замещен после таяния льда таким же объемом воды, что означает: уровень воды в сосуде не изменится. Ответ — 3
Ответ: 23
На поверхности воды плавает деревянный брусок плотностью (rho_1)=700 кг/м(^3). Как изменятся следующие величины: уровень воды и сила Архимеда, действующая на брусок, если заменить деревянный брусок, на брусок такого же объема, но плотностью (rho_2 )=1400 кг/м(^3)?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Уровень воды}&text{Сила Архимеда}\
hline
&\
hline
end{array}]
1) Объем погруженной части равен объему вытесненной жидкости, а так как (rho_2>rho_1), то тело погрузится глубже, а значит и уровень воды увеличится. Ответ — 1
2) Сила архимеда находится по формуле: [F_text{a}=rho_text{в}g V_text{п}] Где (rho_text{в}) — плотность воды, а (V_text{п}) — объем тела погруженного в воду. Так как (rho_2 >rho_text{в}), то тело тонет в жидкости и объем погруженной части увеличивается, а следовательно и увеличивается сила Архимеда. Ответ — 1
Ответ: 11
В сосуде, наполненным водой, проводят 3 опыта. Опыт 1: кладут брусок плотностью (rho_2)=1400 кг/м(^3). Опыт 2: кладут брусок плотностью (rho_3)=2100 кг/м(^3). Опыт 3: вначале брусок плотностью (rho_2)=1400 кг/м(^3), а затем брусок того же объема, но плотностью (rho_3)=2100 кг/м(^3). Как изменится сила Архимеда в опыте 2 относительно опыта 1 и уровень воды в опыте 3?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда в опыте 2 относительно опыта 1}&text{Уровень воды в опыте 3}\
hline
&\
hline
end{array}]
1) Так как (rho_2) и (rho_3) больше (rho_text{в}), где (rho_text{в}) — плотность воды, то бруски в опытах 1 и 2 тонут , а значит погружаются на полный объем. Сила архимеда находится по формуле [F_text{a}=rho_text{в}g V_text{п}] Где (rho_text{в}) — плотность воды, а (V_text{п}) — объем тела погруженного в воду. Так как плотность жидкости одинаковая и объем погруженного тела одинаковый, то и сила Архимеда одинаковая. Ответ — 3
2) Как выяснили в 1) бруски плотностью (rho_2) и (rho_3) тонут в воде, а значит и вытесняют одинаковый объем жидкости, следовательно и уровень жидкости не изменяется. Ответ — 3
Ответ: 33
К деревянному бруску, плавающему в воде, привязали на тонкой нити небольшой стальной шарик, после привязывания система находится в равновесии. Как изменятся следующие величины: сила архимеда, действующая на брусок, и уровень воды? Считать, что брусок не утонул.
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда, действующая на брусок}&text{Уровень воды}\
hline
&\
hline
end{array}]
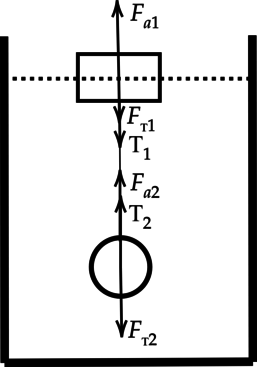
Обозначим все силы, действуюющие только на брусок: 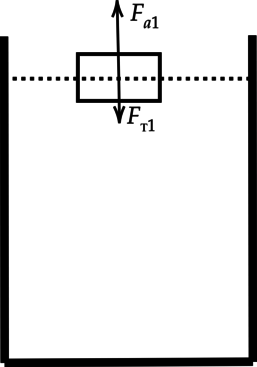
Обозначим все силы, действующие на систему брусок+шарик: 
1) Как мы видим на первом рисунке ( F_ text{a1}=F_text{т1} ). На втором рисунке распишем все силы: [F_text{a1}+F_text{a2}+ T_2=F_text{т1}+F_text{т2}+T_1] Так как (T_1=T_2), то можно заменить [F_text{a1}+F_text{a2}=F_text{т1}+F_text{т2}] Кроме того, шарик, сделанный из стали, тонет в воде, а значит (F_text{т2}>F_text{a2}). Значит, и (F_text{a1}) должна увеличится, для того, чтобы равенство соблюдалось. Ответ — 1
2) Сила Архимеда находится по формуле: [F_text{а}=rho g V] где (rho) — плотность жидкости, (V) — объем погруженной части тела в жидкость. Так как сила Архимеда увеличилась, а плотность осталась неизменной, то (V) увеличился, значит и количество вытесненной воды увеличится и уровень воды поднимется. Ответ — 1
Ответ: 11
На поверхности воды плавает деревянный брусок. Как изменятся сила Архимеда, действующая на брусок, и масса вытесненной воды, если брусок заменить на другой с той же массой (m), но меньшей плотностью (rho)?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Масса вытесненной воды}\
hline
&\
hline
end{array}]
1) Так как брусок плавает на поверхности, то сила Архимеда уравновешивает силу тяжести. [F_a=mg] Так как масса не изменилась, то и сила Архимеда не изменилась. Ответ — 3
2) Сила Архимеда находится по формуле: [F_a=rho_1gV] Где (rho_1) — плотность жидкости, а (V) — объем погруженной части тела в жидкость. В пункте 1) доказали, что сила Архимеда не изменилась, а так как (rho_1) осталась неизменной, то и (V) тоже не изменился. Значит и масса вытесненной воды не изменилась. Ответ — 3
Ответ: 33
Источник
1
Урок «Изменение уровня жидкости в сосуде» Авторы-составители: Н.В. Ларионова, к.п.н., учитель физики высшей категории; В.С.Ларионов, учитель физики высшей категории.
2
ЗАДАЧА В цилиндрическом сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лёд растает? ?
3
ЦЕЛЬ УРОКА Изучить 2 способа решения задач об изменении уровня жидкости в сосуде. Сформулировать алгоритмы решения. ЦЕЛЬ УРОКА
4
2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно
5
АНАЛИЗ V 0 – первоначальный объём жидкости в сосуде, V 1 – «добавочный» объём, V 2 – «добавочный» объём после некоторых манипуляций с содержимым сосуда, S – площадь дна сосуда, h 0, h 1, h 2 – уровни жидкости в сосуде. V 0 +V 1 =Sh 1 V 0 +V 2 =Sh 2
6
1.Запишем условие плавания для кусочка льда: Fа = Fт. Fа = Fт. 2.Воспользуемся законом Архимеда: ρ ж gV в.ж = m л g, где m л – масса льда, V в.ж (V 1 ) – объём вытесненной жидкости. 3. Откуда V в.ж = m л /ρ ж. 4. После таяния льда объём воды в сосуде увеличился на ΔV (V 2 ) ΔV= m л /ρ ж. (Очевидно, что масса талой воды равна массе льда.) 5. Откуда следует, что V в.ж. = ΔV, т.е. h 1 = h 2. РЕШЕНИЕ
7
ОТВЕТ: Уровень воды в сосуде не изменится.
8
1. Записать условие плавания тела: F т = F а. (1) 2. Воспользоваться законом Архимеда: F а = ρ ж gV в.ж. (2) 3. Используя уравнения (1) и (2) и расписав F т выразить объём вытеснённой жидкости V в.ж. (V 1 ) 4. Рассчитать на сколько измениться уровень воды в сосуде по сравнению с изначальным (до погружения тела в воду) после таяния льда (или других действий): Δ V ( V 2 ). 5. Сравнить V в.ж. (V 1 ) с Δ V ( V 2 ) и сформулировать ответ. АЛГОРИТМ решения задачи через объёмы
9
2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно 1. F т = F а 2. F а = ρ ж gV в.ж 3. V 1 4. V 2 5. V 1 ? V 2
10
h1h1 h2h2 1.С одной стороны, силу давления на дно в 1-ом и во 2-ом случаях можно выразить следующим образом F д1 = (m л +М)g, F д2 = (m в +М)g, где m л – масса льда, M – первоначальная масса воды в стакане без льда, m в – масса воды, образовавшейся после таяния льда. Т.к. m л = m в, то F д1 = F д2. 2. С другой стороны: F д1 = p 1 S = gh 1 S, F д2 = p 2 S = gh 2 S. 3. Т.к. F д1 = F д2, то h 1 = h 2. РЕШЕНИЕ
11
ОТВЕТ: Уровень воды в сосуде не изменится.
12
1. Содержимое сосуда не изменилось, поэтому не изменилась и сила давления на дно сосуда: F д1 = F д2. (1) 2. Выразить F д1 и F д2, воспользовавшись определительной формулой давления p = F д /S и формулой гидростатического давления p= ρ gh : F д1 = …, F д2 =… (2) 3. Из уравнений (1) и (2) выразить высоты h 1 и h 2 и сравнить. АЛГОРИТМ решения задачи через давление на дно сосуда
13
2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно 1. F т = F а 2. F а = ρ ж gV в.ж 3. V в.ж. 4. Δ V. 5. V в.ж. ? Δ V 1. F д1 = F д2. 2. p = F д /S F д1 = … p= ρ gh F д2 =… 3. (1) и (2) h 1 ? h 2
14
через объёмычерез давление на дно 1. F т = F а 2. F а = ρ ж gV в.ж 3. V 1 4. V 2 5. V 1 ? V 2 1. F д1 = F д2. 2. p = F д /S F д1 = … p= ρ gh F д2 =… 3. (1) и (2) h 1 ? h 2 Алгоритмы Изучить 2 способа решения задач об изменении уровня жидкости в сосуде. Сформулировать алгоритмы решения. ЗАДАЧИ УРОКА
15
1. В цилиндрическом сосуде с водой плавает кусок льда, в котором находится пузырёк воздуха. Изменится ли уровень воды в сосуде, если лёд растает? 2. В цилиндрическом сосуде с водой плавает кусок льда с вмёрзшим в него стальным шариком. Изменится ли уровень воды в сосуде, если лёд растает? 3. В цилиндрическом сосуде на поверхности воды плавает стальная кастрюля. Изменится ли уровень воды в сосуде, если кастрюлю утопить? 4. В небольшом бассейне плавает лодка. Как изменится уровень воды в бассейне, если лежащий на дне лодки камень бросили в воду? 5. В небольшом бассейне плавает полузатопленная лодка, причём уровень воды в лодке совпадает с уровнем воды в бассейне. Из лодки зачерпнули ведро воды и вылили в бассейн. Как изменился уровень воды в бассейне? КЛЮЧЕВЫЕ ЗАДАЧИ
16
Библиография 1. Гельгафт И.М., Генденштейн Л.Э., Кирик Л.А задача по физике с решениями. Учебное пособие. – Харьков-Москва, – 592 с. 2. Городские олимпиады по физике г. Нижнего Новгорода гг. Сборник задач. – Н.Новгород: Институт прикладной физики РАН, –52с. 3. Подлесный Д.В. Анализ давления на дно сосуда в задачах гидростатики. // Потенциал, 10, – С Полянский С.Е. Поурочные разработки по физике. – М.: ВАКО, –240с. 5. Черноуцан А. Гидростатика в стакане. // Квант, 3, – С Чивилёв В.И. Олимпиада «Физтех-2005». // Потенциал, 5, – С.59-61
Источник
