В большой сосуд с водой был
Задачи, тесты
Е. М. Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5, 8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где – объём погружённой части коробочки. Подставляя числовые данные, получаем
Отсюда глубина погружения коробочки равна
Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:
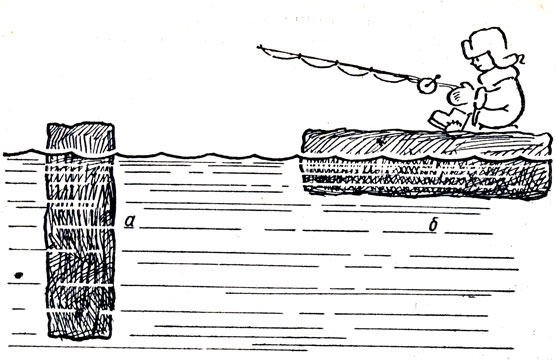
20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:
23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина
Решая совместно оба уравнения, получаем:
24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению:
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле полученной при решении задачи 9 (см. № 5/2010):
– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:
Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:
26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна
Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
Задача по физике – 4962
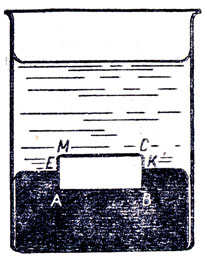
В сосуде с водой плавает стакан, в котором находится камень. Как изменится уровень воды в сосуде, если из стакана вынуть камень и опустить его в сосуд?
Решение. При перенесении камня в сосуд общий вес воды, камня и стакана не меняется. Площадь дна сосуда тоже не меняется. Следовательно, давление системы трех тел на дно сосуда не должно измениться. Но давление столба воды на дно сосуда $p = rho gh$, где $rho$ – плотность воды, $g$ – ускорение силы тяжести, $h$ – высота столба. Следовательно, уровень воды в сосуде не должен измениться.
Проделаем соответствующий опыт и убедимся, что уровень воды в сосуде понизится. В чем ошибочность решения?
Подробнее
Задача по физике – 4963
В сосуде со ртутью плавает чугунный брусок. Изменится ли положение центра тяжести бруска по отношению к уровню ртути, если в сосуд налить воды?
Решение. Вода давит на брусок сверху и с боков. Силы давления на брусок с боков уравновешиваются, а сила давления на брусок сверху должна понизить положение центра тяжести бруска по отношению к уровню ртути.
Проделаем соответствующий опыт и обнаружим, что брусок в ртути не опускается, а немного всплывает. В чем ошибочность представленного выше решения?
Подробнее
Задача по физике – 4964
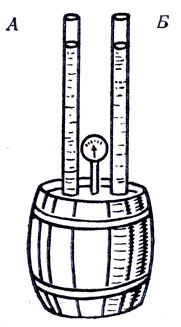
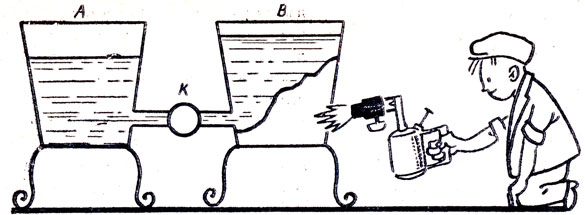
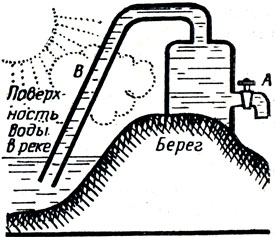
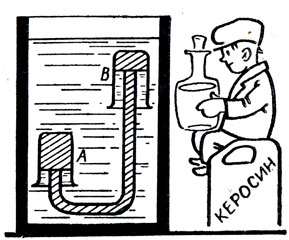
Обычно считают, что сифоном можно переливать жидкость из верхнего сосуда в нижний. Если в большой сосуд с водой поместить два сосуда А и В, причем в первом находится керосин, а во втором – вода (рис.), и соединить их трубкой, то керосин будет переливаться из нижнего сосуда А в верхний сосуд В.
Таким образом, керосин, всплывая, увеличивает свою потенциальную энергию по отношению к Земле. Не противоречит ли этот опыт закону сохранения энергии?

Подробнее
Задача по физике – 4965
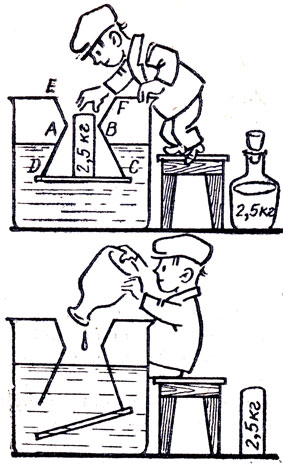
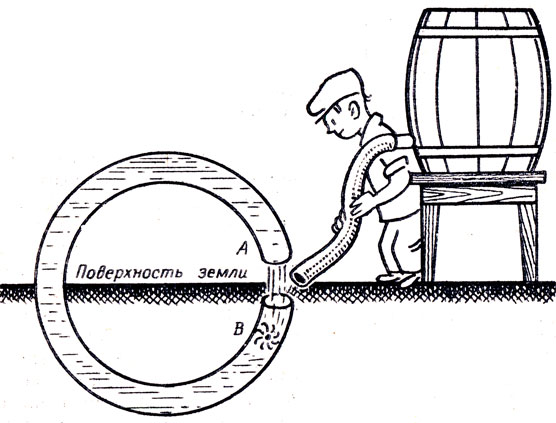
Кювета с водой стоит на бруске (рис.). На воде плавает коробочка с гирей. Кювета находится в равновесии.
Если вынуть гирю из коробочки и поставить на дно кюветы под тем местом, где плавала коробочка, то равновесие нарушится (рис.), хотя вес левой части кюветы как будто бы не изменился. Объясните ошибку рассуждений

Подробнее
Задача по физике – 4966
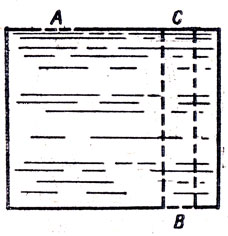
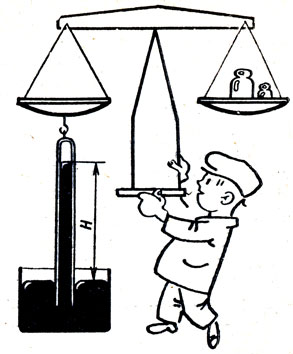
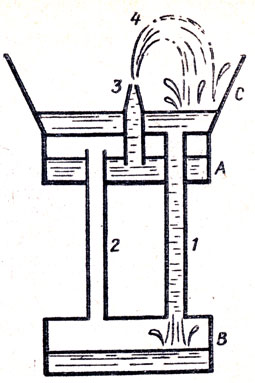
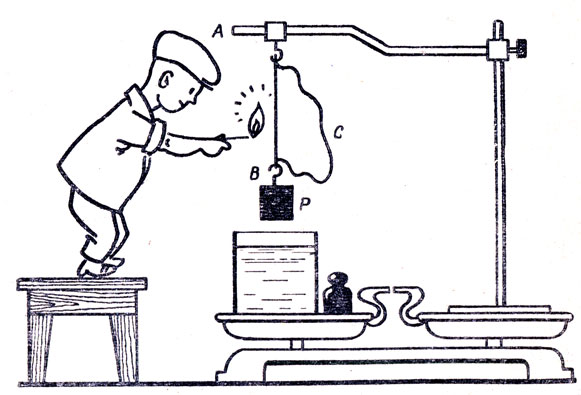
Если в установке, изображенной на рисунке, пережечь нить АВ, то тело Р, имеющее объем 100 $см^{3}$, целиком погружается в воду и остается висеть на нити АСВ. При этом равновесие весов нарушается. На какую чашку весов и какой добавочный груз необходимо положить, чтобы восстановить равновесие?
Решение. В соответствии с законом Архимеда тело Р, погруженное в воду, будет выталкиваться вверх с силой 0,98 н. Поэтому на правую чашку весов будет действовать вес штатива и вес тела Р, уменьшенный на вес вытесненной им воды.
Следовательно, для восстановления равновесия весов необходимо на правую чашку поставить гирю массой 100 г.
Однако опыт показывает, что на правую чашку весов необходимо поставить гирю массой 200 г. В чем ошибка решения?

Подробнее
Задача по физике – 4967
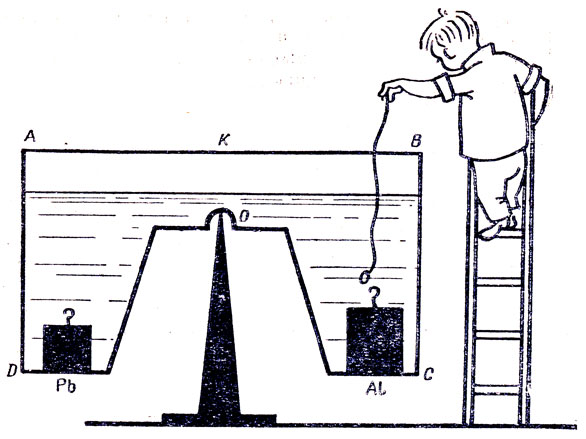
Симметричный относительно вертикальной плоскости ОК сосуд ABCD (рис.) наполнен водой и опирается о ребро неподвижной призмы. В правую часть сосуда опустили кусок алюминия массой 0,5 кг, а в левую – кусок свинца массой 0,4 кг. Какая часть сосуда перетянет?
Решение. Сосуд представляет собой сложный равноплечий рычаг. Так как вес куска алюминия больше, чем свинца, то перетянет правая сторона сосуда, где лежит кусок алюминия.
Опыт, однако, опровергает это заключение. В чем ошибка решения?

Подробнее
Задача по физике – 4968
В высокий стеклянный цилиндрический сосуд помещают песочные часы, наливают воды до самого верха и закрывают крышкой (рис.). Часы всплывают под самую крышку. Затем цилиндр переворачивают. Часы не всплывают (рис.), хотя они окружены водой и выталкивающая сила больше веса часов. Через определенный промежуток времени, когда некоторое количество песка высыплется в нижнее отделение, часы начнут медленно всплывать. Таким образом, перетекание песка из верхнего отделения часов в нижнее влияет на его плавучесть. Но ведь часы герметически закрыты и вес их от перетекания песка не изменяется. Как объяснить этот парадокс?

Подробнее
Задача по физике – 4969
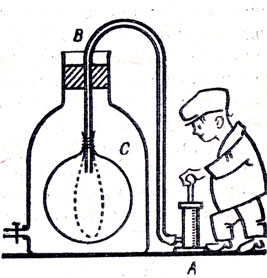
Взлет космического корабля с Земли происходит с ускорением, в несколько раз превышающим ускорение силы тяжести. Поэтому находящийся в корабле космонавт подвергается действию перегрузки (силы, прижимающей человека к опоре).
Чтобы избежать перегрузки, предлагают помещать космонавта в камеру с водой (плотность воды примерно равна плотности человеческого тела). Авторы проекта считали, что человек, находясь в воде, становится невесомым и, следовательно, совершенно избавляется от действия как естественной, так и искусственной тяжести (перегрузки). В чем состоит ошибка такого заключения?
Подробнее
Задача по физике – 4970
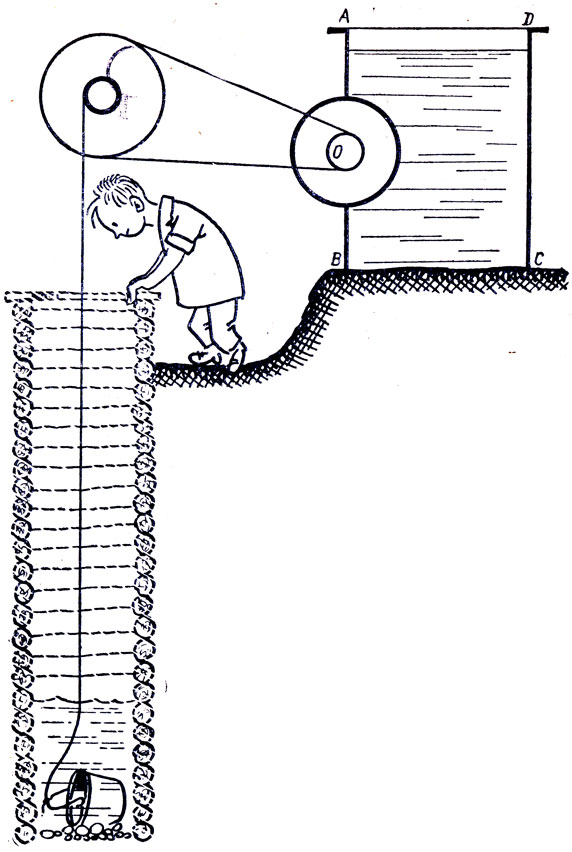
Рассмотрим один из проектов вечного двигателя. В вырез стенки АВ бака с жидкостью вставлен вал (рис.), ось которого О лежит в плоскости стенки АВ. Вал закрывает собой весь вырез, так что жидкость не выливается; вал может вращаться на своей оси. На половину вала, погруженную в жидкость, по закону Архимеда действует подъемная сила, которая, по мысли изобретателя, должна вызвать вращение вала против часовой стрелки. Это вращение должно было бы продолжаться вечно. В чем ошибка проекта?

Подробнее
Задача по физике – 4971
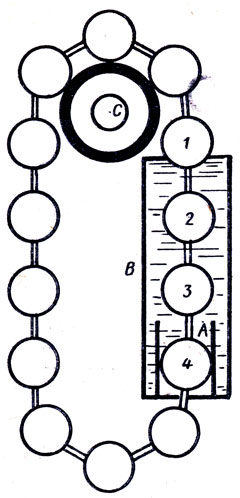
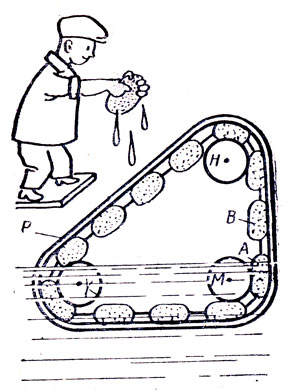
Швейцарец Г. Леонард в 1865 г. предложил следующий проект вечного двигателя. Бесконечная цепь из жестяных поплавков проходит правой половиной сквозь сосуд В с водой (рис.). По мысли автора, поплавки, стремясь всплыть, будут вращать колесо С, через которое эта цепь переброшена, против движения часовой стрелки. В чем ошибка проекта?

Подробнее
Задача по физике – 4972
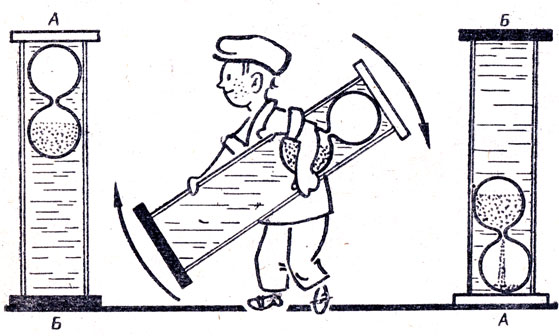
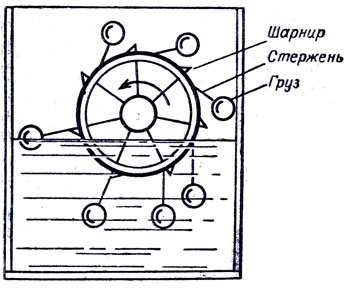
В XV в. был предложен проект вечного двигателя, основанный на законе Архимеда. В проекте этого вечного двигателя имеется колесо с семью откидывающимися на шарнирах грузами (рис.). Изобретатель погрузил одну треть колеса в воду, обоснованно предполагая, что вес этой части колеса и грузов уменьшится по известному закону Архимеда и колесо придет во вращение. В чем ошибка проекта?

Подробнее
Задача по физике – 4973
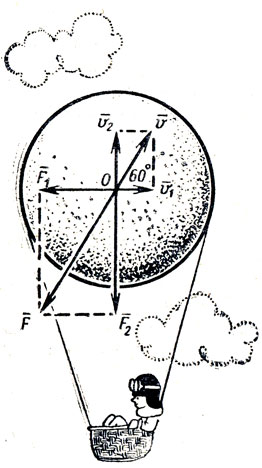
Шар движется в воздухе, имея в данный момент скорость $v$ (рис.). Так как сила сопротивления воздуха пропорциональна квадрату скорости, то ее можно представить в виде $F = kv^{2}$, где $k$ – коэффициент пропорциональности.
С другой стороны, разложив скорость $v$ на горизонтальную и вертикальную составляющие, получим: $v_{1} = v cos 60^{ circ}$ и $v_{2} = v sin 60^{0}$. Следовательно, $F_{1} = kv_{1}^{2} = kv^{2} cos^{2} 60^{ circ}$ и $F_{2} = kv_{2}^{2} = kv sin^{2} 60^{ circ}$, где $F_{1}$ и $F_{2}$ – силы сопротивления, вызванные составляющими $v_{1}$ и $v_{2}$. Таким образом, полная сила сопротивления равна:
$F = sqrt{ F_{1}^{2} + F_{2}^{2}} = sqrt{(kv^{2} cos^{2} 60^{ circ}) + (kv^{2} sin^{2} 60^{ circ})} = kv^{2} sqrt{ frac{5}{8}}$
что не совпадает с выражением $F=kv$. Как разрешить это противоречие?

Подробнее
Задача по физике – 4974
Все тела падают на землю. Облака состоят из мелких капелек воды. Значит, облака должны падать на землю.
Однако никому не удавалось наблюдать, чтобы облако, опускаясь, когда-нибудь достигло земли. Как разрешить этот парадокс?
Подробнее
Задача по физике – 4975
При испытании реактивного снаряда, установленного в хвосте самолета для его защиты от нападения сзади, был обнаружен удивительный парадокс. При выпуске снаряда он сначала удалялся от самолета, а затем разворачивался и догонял самолет. Как можно объяснить это явление?
Подробнее
Задача по физике – 5135
В одном из солёных озёр Канады плотность воды зависит от глубины так, как показано на рис. На какой глубине и в каком положении будет плавать тонкая однородная палка? Плотность материала, из которого она сделана, равна 1020 $кг/м^{3}$.

Подробнее
Источник
4. –○47. , , , ( ). (. 26) , . .
. 26 ○48. . (. 27) , – , , ; , , . ?
. 27 ●49. (. 48) . , , . , (. 28), .
. 28 , 28. , , , . ? ○50. . EADCBF CD (. 29). ABCD 2,5 , , 24,5 . CD 25 , , 2,5 , . .
. 29 ○51. . : – , , , . (. 30), , . , , .
. 30 , , , – , , -. , , – . ? ●52. . , , , 31. . , , . , , ?
. 31 ●53. . (. 32). , . , ?
. 32 . , . , , , . , . , . , , , . ? ●54. . , (. 33), . , , , . , , 2-3 , ( ) , , . ., . , ,- , . ? ?
. 33 ○55. ? , 20, , , . , . . . . . , . ? ○56. ? (. 34). . , , . ( ) , , ?
. 34 ●57. “” . “” . (), (. 35). , . , ( ) , . ?
. 35 ●58. “” . , , 36, . . , ? .
. 36 . . . . ? ○59. ? , 15-20 , 300 (. 37). , 1 . . , . , . . ?
. 37 ●60. ? , , . , . , , . , ? ●61. . (. 38). . : , 1, , 2, , 3, 4, . .? ( , ), : 4 , ?
. 38 ○62. ? (. 39) . , . . , , , . .
. 39 ●63. . , . , ? . , . . , . =ρ, ρ – , g – , h – . , . , . ? ●64. ? , (. 40). , .
. 40 . , . , . , , , . , , , , , . , , , . , , , . , . ? ○65. . . , (. 64)? . . , . , , . ? ○66. ? , , . 41 . , , . ?
. 41 ○67. ? , , , . , ” “. ? ○68. ? , . , , – (. 42), , .
. 42 , , , . ? ○69. . . , ( 6 ) , , 6 , . , , , . ? ●70. ? (. 43). . .
. 43., . 44 , , (. 44), . . ●71. ? , 45, , , 100 3, . . , ?
. 45 . , , 0,98 . , . , 100 . , 200 . ? ●72. ? ABCD (. 46) . 0,5 , – 0,4 . ?
. 46 . . , , , . , , . ? ○73. . , (. 47). . . (. 48), . , , . , . . ?
. 47., . 48 ●74. ? , . (, ). , ( ). , , , , , , (). ? ●75. . . (. 49), .
. 49 , ; . , , , , , . . ? ●76. . . 1865 . . (. 50). , , , , , . ?
. 50 ●77. . XV . , 1. (. 51). , , . ? 1 ()
. 51 ●78. . . , , , , (. 52). . , . . , , , . , (. . ), , . … . ?
. 52 ●79. . , v (. 53). , F=kv2, k – .
. 53 , v , : v1 = vcos60 v2 = vsin60. , F1 = kv12 =kv2cos260 F2 = kv22 = kv2sin26O, F1 F2 – , v1 v2. , : F = kv2. ? ○80. ? . , , . , , , – . ? ○81. . , , . , . ? www.baltprofile.ru. 24xxx.me//armyanki/ |
Источник