В чем измеряется вместимость сосуда

У этого термина существуют и другие значения, см. Объём (значения).
Объём – количественная характеристика пространства, занимаемого телом или веществом. С понятием объёма тесно связано понятие вместимости – объёма внутреннего пространства сосуда, упаковочного ящика и т. п. Объём тела (как и вместимость сосуда) определяется его формой и линейными размерами. Основное свойство объёма – аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей[1].
Единица объёма в СИ – кубический метр; от неё образуются производные единицы – кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма – галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume – «объём», «наполнение».
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма[править | править код]
На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.
Математически[править | править код]
Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром вычисляется с помощью выражения , а объём прямоугольного параллелепипеда – умножением его длины на ширину и на высоту.
Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.
Сводка формул[править | править код]
Через плотность[править | править код]
Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: .
Единицы объёма жидкости[править | править код]
- 1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона
Русские[2][править | править код]
- Ведро = 12,3 литра
- Бочка = 40 вёдер = 492 литра
Английские[править | править код]
- 1 пинта = 0,568 литра
- 1 кварта (жидкостная) = 2 пинтам = 1,136 литра
- 1 галлон = 8 пинтам = 4,55 литра
- 1 галлон (амер.) = 3,785 литра
Античные[править | править код]
- Котила = 0,275 литра
Древнееврейские[3][править | править код]
- Эйфа = 24,883 литра
- Гин = 1/6 эйфы = 4,147 литра
- Омер = 1/10 эйфы = 2,4883 литра
- Кав = 1/3 гина = 1,382 литра
Единицы объёма сыпучих веществ[править | править код]
Русские[править | править код]
- Четверик = 26,24 литра (1 пуд зерна)
- Гарнец = 3,28 литра
- Четверть = 1/4 ведра = 3,075 литра
- Штоф = 1/8 ведра = 1,54 литра
- Кружка = 1/10 ведра = 1,23 литра
- Бутылка (винная) = 1/16 ведра = 0,77 литра
- Бутылка (пивная) = 1/20 ведра = 0,61 литра
- Чарка = 1/10 кружки = 0,123 литра
- Шкалик (косушка) = 1/2 чарки = 0,0615 литра
Английские[править | править код]
- 1 бушель = 8 галлонов = 36,36872 литра
- 1 баррель = 163,65 литра
Прочие единицы[править | править код]
- 1 унция (англ.) = 2,841⋅10−5 м³
- 1 унция (амер.) = 2,957⋅10−5 м³
- 1 кубический дюйм = 1,63871⋅10−5 м³
- 1 кубический фут = 2,83168⋅10−2 м³
- 1 кубический ярд = 0,76455 м³
- 1 кубическая астрономическая единица =3,348⋅1024 км³
- 1 кубический световой год = 8,466⋅1038 км³
- 1 кубический парсек = 2,938⋅1040 км³
- 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅1049 км³
Примечания[править | править код]
Литература[править | править код]
- Объём // Математическая энциклопедия (в 5 томах). – М.: Советская Энциклопедия, 1982. – Т. 3.
- Объём // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). – СПб., 1890-1907.
Ссылки[править | править код]
- Формулы объёма и программы для расчета объёма. Дата обращения: 26 ноября 2020.
Источник
Что такое вместимость сосуда
Вместимость сосуда – это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ – кубический метр, но в случае жидкости чаще используют литр.
Особенности расчета объема жидкости в сосуде
Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества – твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.
В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.
За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:
(h = frac{p}{rho s g}.)
(p) здесь – давление в паскалях, (rho) – плотность, (g) – ускорение свободного падения, константа.
Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.
При решении логических учебных задач на переливание жидкости из одного сосуда в другой может пригодиться понимание взаимосвязи объема жидкости и параметров сосуда. А для задач по физике часто требуется рассчитать объем, который занимает жидкость в сосуде, через ее массу. На практике это действительно один из самых удобных способов, не требующий ни специальных датчиков, ни сложных расчетов.
Задача
Найти объем керосина, зная массу одного и того же сосуда с ним, и без него. Масса пустого сосуда 440 грамм, полного – 600 грамм.
Решение:
Плотность керосина можно узнать из справочной таблицы – 800 (frac{кг}{м^{3}}.)
Вычислим массу керосина в сосуде: 600 – 440 = 160.
Подставим известные данные в формулу:
(V = frac{m}{rho} = frac{0,16}{800} = 0,0002 м^{3} = 200 см^{3}.)
Ответ: 200 (см^{3}.)
Как определить вместимость сосудов разных форм
Вычисление объема параллелепипеда
Параллелепипед – это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.
(V = S_{осн} s H. )
Прямоугольный параллелепипед – это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, – это куб.
Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:
(V = AB s AD s AA_{1} = abc.)
Объем куба равен кубу его стороны:
(V = a^{3}.)
Нахождение объема пирамиды
Пирамида – это многогранник, состоящий из основания – плоского многоугольника, вершины – точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды – это перпендикуляр, опущенный из вершины на плоскость основания.
(V = frac{1}{3} s S_{осн} s h.)
Чтобы определить объем усеченной пирамиды, надо знать площадь обоих оснований – (S_{1}) и (S_{2}).
(V = frac{1}{3} s h s (S_{1} + S_{2} + sqrt{S_{1} s S_{2}}). )
Как найти объем цилиндра
Цилиндр – это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
(R) – радиус основания цилиндра, (h) – его высота, равная образующей оси.
(V = S_{осн} s h = pi s R^{2} s h.)
Если нужно найти объем усеченного цилиндра, то понадобится не только R – радиус основания, но и наибольшая и наименьшая образующие. Они обозначаются буквой l – (l_{1}) и (l_{2}).
(V = pi s R^{2} s frac{l_{1} + l_{2}}{2}.)
Как высчитать объем конуса
Конус – это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.
(V = frac{1}{3} s S_{осн} s h = frac{1}{3} s pi s R^{2} s h.)
Чтобы найти объем усеченного конуса, понадобятся (R_{1}) и (R_{2}) – радиусы оснований, а также высота (h).
(V = frac{pi s h}{3} s (R_1^2 + R_2^2 + R_1 s R_2).)
Нахождение объема шара
Шар – это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.
(R) – радиус полукруга, равный радиусу шара.
(V = frac{4pi s R^{3}}{3}.)
Источник
Объём количественная характеристика, занимаемого телом или веществом.
Общие сведения.
Объём тела или вместимость сосуда определяется его формой и линейными размерам. Под вместимость часто понимают объем.
Общий метод вычисления объема геометрических фигур получен с помощью интегрального исчисления.
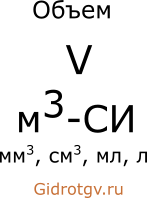
В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. volume – «объём», «наполнение».
Определение объема (вместимости) на практике решают несколькими способами:
- математически – разбиением тела на отдельные части простой формы и суммированием объёмов этих частей;
- расчетом по известной массе и плотности тела (физическая формула) – V=m/ρ, где m – масса тела; ρ – плотность тела;
- возможен расчет объема газа по уравнениям идеального или реального газа по известным параметрам (давление, молярная масса, температура и т.д.);
- измерениями:
- объема тела через объем вытесненной жидкости – погрузив тело в жидкость. Объём вытесненной жидкости будет равен объёму измеряемого тела;
- внутреннего объема тела путем заполнения его жидкостью и последующим измерением объема этой жидкости;
- разницы массы между сосудом пустым и заполненным водой. С последующим вычислением объема через плотность и массу.
Перевод единиц измерения объема онлайн:
Калькулятор объема. Перевод единиц измерения объема (мм3, см3, мл, л, дм3, м3 и т.д.)
Результат перевода единиц измерения объема (VV)
Результаты работы калькулятора объема при переводе в другие единицы измерения объема:
Примеры результатов работы калькулятора объема:
Поделится ссылкой на расчет:
Единицы измерения объема.
- кубический миллиметр- обозначение на сайте мм3;
- кубический сантиметр – обозначение на сайте см3;
- кубический миллилитр – обозначение на сайте мл;
- кубический литр – обозначение на сайте л. Внесистемная единица измерения объема. Допускаются к применению в России без ограничения срока наравне с единицами СИ с областью применения «все области». Данная единица измерения широко применяется при инженерных расчетах, в современной справочной литературе, в обозначение параметров оборудования, технических устройств, при разработке проектной и рабочей документации;
- кубический дицеметр – обозначение на сайте дм3;
- кубический метр – единица измерения объема в СИ. Обозначение в России: м3; международное: m3. Данная единица измерения широко применяется при инженерных расчетах, в современной справочной литературе, в обозначение параметров оборудования, технических устройств, при разработке проектной и рабочей документации.
Перевод единиц измерения объема (в табличном виде).
| Переводимые единицы измерения объема | Перевод объема в единицы измерения: | |||||
| мм3 | см3 | мл | л | дм3 | м3 | |
| мм3 | 1 | 10-3 | 10-3 | 10-6 | 10-6 | 10-9 |
| см3 | 103 | 1 | 1 | 10-3 | 10-3 | 10-6 |
| мл | 103 | 1 | 1 | 10-3 | 10-3 | 10-6 |
| л | 106 | 103 | 103 | 1 | 1 | 10-3 |
| дм3 | 106 | 103 | 103 | 1 | 1 | 10-3 |
| м3 | 109 | 106 | 106 | 103 | 103 | 1 |
Порядки единиц измерения объема.
| Порядок единиц измерения | Единицы измерения | |||
|---|---|---|---|---|
| мм3 | см3 | м3 | мл | |
| 10 | – | – | – | – |
| 100 | – | – | – | – |
| 1 000 | см3 | – | – | л |
| 10 000 | – | – | – | – |
| 1 000 000 | – | м3 | – | – |
Видеоматериал по теме «Объем».
Калькуляторы объема:
Онлайн калькуляторы объема тел с простыми объемами.
Калькулятор Объема куба.
Введите длину стороны куба (a1)
Результат расчета объема куба (Vkub)
Формула расчета объема куба:
Скачать результат расчета объема куба:
Поделится ссылкой на расчет объема:
Калькулятор Объема прямоугольной призмы.
Введите длину стороны призмы (a2)
Введите длину стороны призмы (b2)
Введите длину стороны призмы (c2)
Результат расчета объема прямоугольной призмы (Vpr)
Формула расчета объема прямоугольной призмы:
Скачать результат расчета объема прямоугольной призмы:
Поделится ссылкой на расчет объема:
Калькулятор Объема пирамиды.
Введите длину высоты пирамиды (H3)
Введите площадь основания пирамиды (S3)
Результат расчета объема прямоугольной призмы (Vpir)
Формула расчета объема прямоугольной призмы:
Скачать результат расчета объема прямоугольной призмы:
Поделится ссылкой на расчет объема:
Калькулятор Объема усеченной пирамиды.
Введите длину высоты усеченной пирамиды (H4)
Введите площадь первого основания усеченной пирамиды (S4n)
Введите площадь второго основания усеченной пирамиды (S4v)
Результат расчета объема прямоугольной призмы (Vuspir)
Формула расчета объема прямоугольной призмы:
Скачать результат расчета объема прямоугольной призмы:
Поделится ссылкой на расчет объема:
Калькулятор Объема конуса.
Введите длину высоту конуса (H5)
Введите длину радиуса основания конуса (R5)
Результат расчета объема конуса (Vkon)
Формула расчета объема конуса:
Скачать результат расчета объема конуса:
Поделится ссылкой на расчет объема:
Калькулятор Объема цилиндра.
Введите длину высоту цилиндра (H6)
Введите длину радиуса цилиндра (R6)
Результат расчета объема цилиндра (Vrad)
Формула расчета объема цилиндра:
Скачать результат расчета объема цилиндра:
Поделится ссылкой на расчет объема:
Калькулятор Объема сферы.
Введите длину радиуса сферы (R7)
Результат расчета объема сферы (Vsf)
Формула расчета объема сферы:
Скачать результат расчета объема сферы:
Поделится ссылкой на расчет объема:
Онлайн калькулятор объема тел через плотность и массу тела.
Введите массу тела/жидкости (mT)
Введите плотность тела/жидкости (pl)
Результат расчета объема тела/жидкости (VT)
Формула расчета объема тела/жидкости:
Скачать результат расчета объема тела/жидкости:
Поделится ссылкой на расчет объема:
Онлайн калькулятор объема газа.
Калькулятор расчета объема газа приведен в теме посвященной идеальному газу.
Поделиться ссылкой:
Источник
