В цилиндрические сообщающиеся сосуды с диаметрами
Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
Помним, (1) что давление в жидкости P = ρ·g·h, (2) если давление в сообщающихся сосудах (в правом и левом колене U образной трубки) одинаково, то жидкость покоится, иначе начинает движение перетекая из одной части сосуда в другую.
Доливая керосин в правое колено трубки мы изменяем уровень воды в левом колене трубки. Но! Вода из правого колена переходит в левое, чтобы скомпенсировать давление создаваемое столбом керосином. Распишем изменение высот столбов жидкости в каждом из колен.
Правое колено:
Высота столба жидкости: h прав. = х + h кер. – h воды., где х-исходная высота столба воды, h кер. -высота столба налитого керосина, h воды. -высота столба воды ушедшей в левое колено сосуда;
Расстояние от края трубки до уровня жидкости: 45 – h кер. + h воды., заметим, что когда жидкость из трубки уходит, то это расстояние увеличивается, когда жидкость доливают, то “зазор” между поверхностью жидкости и краем трубки, увеличивается.
Левое колено:
Высота столба жидкости: h лев. = х + h воды.;
Расстояние от края трубки до уровня жидкости: 45 – h воды.
В тот момент, когда жидкости покоятся, давления в правом и левом колене сосуда равны.
P прав. = P лев.
ρ воды·g·(х – h воды.) + ρ кер. ·g·h кер. = ρ воды ·g·(х + h воды.).
Домножим правую и левую части уравнения на дробь 1/g, раскроем скобки и получим:
ρ воды·х – ρ воды·h воды. + ρ кер. ·h кер. = ρ воды. ·х + ρ воды. ·h воды.
Сгруппируем в правой части уравнения все слагаемые с ρ воды., а в левой с ρ кер.
ρ кер. ·h кер. = ρ воды. ·х + ρ воды. ·h воды. – ρ воды·х + ρ воды·h воды.
ρ кер. ·h кер. = 2·ρ воды. ·h воды.
Плотность пресной воды 1 г/см³ плотность керосина пусть будет 0,8 г/см³ (точное значение зависит от марки керосина).
0,8·h кер. = 2·1·h воды.;
h кер. = (2·1·h воды.) /0,8;
h кер. = 2,5·h воды. [*]
Керосин легче воды, его столб будет выше, поэтому первым исчезнет зазор в правом колене.
45 – h кер. + h воды. = 0, то есть
h кер. = 45 + h воды. [**]
Левые и правые части уравнений [*] и [**] равны, объединим их в одно уравнение.
2,5·h воды. = 45 + h воды.
Упростим выражение.
2,5·h воды. – h воды. = 45;
(2,5 – 1)·h воды. = 45;
h воды. = 45/1,5 = 30 см;
h кер. = 45 + h воды. = 45+30=75 см.
Задача №2
Условие в этой задаче не полное, поэтому она, записанная как есть, имеет множество решений.
p ртути = ρ ртути ·g·h ртути = 13600 кг/м³ · 9,8 Н/кг · 0,01 м = 1333 Па
(Учебник физики 7 класс, Перышкин А. В., 2006 г., стр. 102).
p общ. = p воды + p керосина = ρ воды ·g·h воды + ρ кер. ·g·h кер. = 9800·h воды +7840·h кер.
1333= 9800·h воды +7840·h кер.
Из Вашего условия большего мы получить не сможем.
Задача №3
Сила тяжести F=mg; сообщающиеся сосуды с различным сечением используют в гидравлических машинах для развития больших сил, перегоняя поршнями жидкость из сосуда с малым сечением (площадью поперечного сечения) в сосуд с большим сечением F₂/F₁ = S₂/S₁.
Доливая керосин сверху мы его массой действуем как-бы на поршень 1.
F₁ = Fтяж. керосина. = m кер. ·g = V кер. ·ρ кер. ·g = S₁ · h кер. · ρ кер. ·g.
F₂ = Fтяж. воды. = S₂ · h воды. · ρ воды. ·g.
Жидкость в сосудах покоится, следовательно, сила с которой действует керосин уравновешена силой с которой действует столб воды:
F₁ = F₂;
S₁ · h кер. · ρ кер. ·g = S₂ · h воды. · ρ воды. ·g.
(h кер. · ρ кер. ·g) / (h воды. · ρ воды. ·g) = S₂/S₁;
(???высота керосина 2 см или 0,2 см ??? Будем считать =2 см)
(0,02·0,8·9,8)/(h воды. ·1·9,8) = 3/1
Выразим неизвестную величину:
(0,02·0,8·9,8)·1= 3·(h воды. ·1·9,8)
h воды. = ((0,02·0,8·9,8)·1)/(3·(1·9,8)) = 0,016/3 = 0,005(3) м ≈ 0,53 см. – изменение уровня воды в широком сосуде.
Источник
4.2. Элементы гидростатики
4.2.5. Сообщающиеся сосуды
Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.
Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:
h 1 h 2 = ρ 2 ρ 1 ,
где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.
Указанный закон справедлив в отсутствие сил поверхностного натяжения.
Если сообщающиеся сосуды заполнены однородной жидкостью
ρ1 = ρ2,
то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):
h1 = h2,
где h1 – высота столба жидкости в левом колене; h2 – высота столба жидкости в правом колене сообщающихся сосудов.
Рис. 4.14
Если сообщающиеся сосуды заполнены разнородными жидкостями
ρ1 ≠ ρ2,
то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение
h 1 h 2 = ρ 2 ρ 1 ,
где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.
Рис. 4.15
Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой
p1 = ρ1gh1,
в правом колене –
p2 = ρ2gh2 + ρ3gh3.
Рис. 4.16
Равенство давлений на указанном уровне
p1 = p2
позволяет записать тождество:
ρ1h1 = ρ2h2 + ρ3h3.
Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.
Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:
- в первом сосуде оказывается масса жидкости
m1 = ρV1 = ρ∆h1S1,
где ρ – плотность жидкости; V1 = S1∆h1 – объем жидкости в первом сосуде; S1 – площадь поперечного сечения первого сосуда; ∆h1 – повышение уровня жидкости в первом сосуде;
- во втором сосуде оказывается масса жидкости
m2 = ρV2 = ρ∆h2S2,
где V2 = S2∆h2 – объем жидкости во втором сосуде; S2 – площадь поперечного сечения второго сосуда; ∆h2 – повышение уровня жидкости во втором сосуде.
Повышение уровней жидкости в обоих сосудах одинаково:
∆h1 = ∆h2 = ∆h,
поэтому масса жидкости, добавленной в систему, определяется формулой
m = m1 + m2 = ρ∆h(S1 + S2).
Выразим отсюда искомое значение ∆h:
Δ h = m ρ ( S 1 + S 2 ) .
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для первого (широкого) сосуда
S 1 = π d 1 2 4 ,
- для второго (узкого) сосуда
S 2 = π d 2 2 4 ,
где d1 = 2d2 – диаметр первого (широкого) сосуда; d2 – диаметр второго (узкого) сосуда.
Отношение площадей
S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4
позволяет найти площадь широкого сосуда:
S1 = 4S2.
Подставив S1 в формулу для ∆h
Δ h = m ρ ( 4 S 2 + S 2 ) = m 5 ρ S 2 ,
рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:
Δ h = 0,12 5 ⋅ 1,6 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 15 ⋅ 10 − 3 м = 15 мм.
Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем – 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.
Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:
p1 = p2,
где p1 – давление в широком сосуде; p2 – давление в узком сосуде.
На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.
Гидростатическое давление на выбранном уровне:
- в широком сосуде
p1 = ρ1gh1,
где ρ1 – плотность жидкости, заполняющей систему изначально; g – модуль ускорения свободного падения; h1 – высота столба жидкости в широком сосуде;
- в узком сосуде
p2 = ρ2gh2 + ρ3gh3,
где ρ2 – плотность первой жидкости, добавленной в узкий сосуд; h2 – высота столба первой жидкости; ρ3 – плотность второй жидкости, добавленной в узкий сосуд; h3 – высота столба второй жидкости.
Равенство давлений на указанном уровне
ρ1gh1 = ρ2gh2 + ρ3gh3
позволяет определить высоту столба жидкости в широком сосуде:
h 1 = 1 ρ 1 ( ρ 2 h 2 + ρ 3 h 3 ) ,
где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:
- для первой жидкости
h 2 = m 2 ρ 2 S 2 ;
- для второй жидкости
h 3 = m 3 ρ 3 S 2 ,
где S2 – площадь поперечного сечения узкого сосуда; m2 – масса первой жидкости, добавленной в узкий сосуд; m3 – масса второй жидкости, добавленной в узкий сосуд.
Подстановка h2 и h3 в формулу для h1 дает
h 1 = 1 ρ 1 ( ρ 2 m 2 ρ 2 S 2 + ρ 3 m 3 ρ 3 S 2 ) = m 2 + m 3 ρ 1 S 2 .
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для широкого сосуда
S 1 = π d 1 2 4 ,
- для узкого сосуда
S 2 = π d 2 2 4 ,
где d1 = 2d2 – диаметр широкого сосуда; d2 – диаметр узкого сосуда.
Отношение площадей
S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4
позволяет найти площадь узкого сосуда:
S 2 = S 1 4 .
Таким образом, высота столба жидкости в широком сосуде определяется выражением
h 1 = 4 ( m 2 + m 3 ) ρ 1 S 1 .
Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:
h 2 + h 3 = m 2 ρ 2 S 2 + m 3 ρ 3 S 2 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) .
Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле
Δ h = ( h 2 + h 3 ) − h 1 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) − 4 ( m 2 + m 3 ) ρ 1 S 1 =
= 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 − ( m 2 + m 3 ) ρ 1 ) .
Произведем вычисление:
Δ h = 4 10 ⋅ 10 − 4 ( 0,12 2,0 ⋅ 10 3 + 0,12 4,0 ⋅ 10 3 − 0,12 + 0,12 6,0 ⋅ 10 3 ) = 0,20 м = 20 см.
Источник
Асламазов Л. Гидростатика // Квант. – 1995. – № 1. – С. 51-55.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Давление и силы давления
Жидкость оказывает давление на стенки сосуда, в котором она находится, или на любую другую поверхность, соприкасающуюся с ней. Давление – величина скалярная. Оно измеряется абсолютной величиной нормальной (перпендикулярной поверхности) силы, действующей со стороны жидкости на единицу площади поверхности:
Давление в различных точках поверхности может быть разным. Поэтому площадь S мы должны брать достаточно маленькой.
По закону Паскаля давление жидкости не зависит от ориентации поверхности. Как бы ни была расположена поверхность в данном месте жидкости, давление на нее будет одним и тем же.
Сила давления всегда перпендикулярна поверхности. В обычных условиях она направлена так, как если бы жидкость стремилась расшириться.
Задача 1. В сосуд, имеющий форму куба с ребром a, налита доверху жидкость плотностью ρ. Определите силы давления жидкости на дно и стенки сосуда.
Давление жидкости на дно сосуда равно весу столба жидкости высотой a с площадью основания, равной единице: , где g – ускореннее свободного падения. (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)
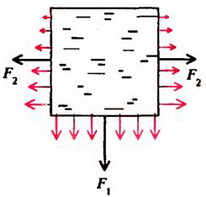
а
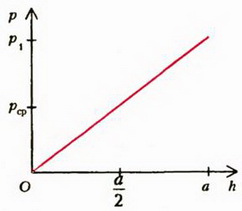
б
Рис. 1
Давление на боковую грань куба будет зависеть от расстояния до поверхности жидкости. На глубине h давление . Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление
умножить на площадь боковой грани
Задача 2. В цилиндрический сосуд диаметром D = 0,7 м вставлен поршень с длинной вертикальной трубкой диаметром d = 0,05 м (рис. 2). Максимальная сила трения между поршнем и стенками сосуда Fтp = 100 Н. Через трубку в сосуд наливают воду. При каком уровне воды в трубке H поршень начнет двигаться? Чему будет равна при этом сила давления воды на дно сосуда? Поршень расположен на высоте h = 0,2 м от дна сосуда. Плотность воды ρ = 103 кг/м3. Массой поршня с трубкой пренебречь.
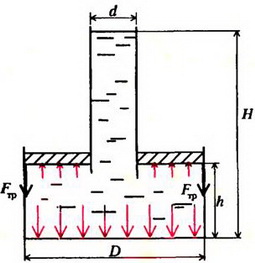
Рис. 2
Давление в жидкости на уровне поверхности поршня определяется расстоянием от этого уровня до свободной поверхности жидкости:
Поршень начнет двигаться, когда сила давления на него со стороны жидкости станет равной максимальной силе трения:
где – плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p1, находим
Давление на дно сосуда .
Сила давления
Задача 3. Длинная вертикальная труба с поршнем опущена одним концом в сосуд с водой. Вначале поршень находится у поверхности воды, затем его медленно поднимают. Как зависит сила, прикладываемая к поршню, от высоты h ее поднятия? Площадь поперечного сечения трубы S, атмосферное давление p0. Изменением уровня воды в сосуде, массой поршня и ею трением о стенки трубы пренебречь.
При поднятии поршня вода под действием атмосферного давления будет вначале заполнять трубу (рис 3, а). Давление в трубе на уровне жидкости в сосуде равно атмосферному давлению p0. Давление воды на поршень меньше атмосферного на величину веса столба жидкости высотой h и площадью основания, равной единице:
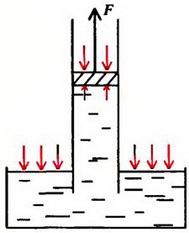
а
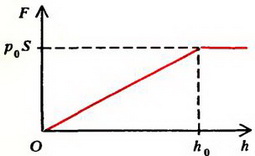
б
Рис. 3
Сверху на поршень по-прежнему действует атмосферное давление. Поэтому для удержания поршня на высоте h к нему надо приложить силу, равную
и направленную вверх.
С увеличением h давление воды на поршень будет уменьшаться. На высоте
давление обратится в ноль. При дальнейшем поднятии поршня уровень воды в трубе изменяться не будет, тан как сила атмосферного давления, действующая на столб жидкости в трубе снизу, уравновесится силой тяжести. Для удержания поршня на высоте h > h0 к нему надо приложить силу .
Зависимость прикладываемой к поршню силы F от высоты его поднятия h изображена графически на рисунке 3, б.
Высота столба воды в трубе , очевидно, может служить для измерения атмосферного давлении p0. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути = 0,76 м (плотность ртути ρрт = 1,36×104 кг/м3).
Примером другого гидростатического устройства, широко используемого в практике, являются сообщающиеся сосуды. Известен закон сообщающихся сосудов: если давление над жидкостью в сосудах одинаково, то уровни жидкости в них равны. Нетрудно доказать этот закон для случая цилиндрических сосудов (рис. 4). Так как жидкость в соединительной трубке находится в равновесии, то давления на нее с обеих сторон должны быть одинаковы. Поэтому равны и уровни жидкости в сосудах.
Рис. 4
В общем случае для доказательства закона сообщающихся сосудов можно воспользоваться принципом отвердевания, который часто используют в гидростатике. Суть этого принципа заключается в следующем: всегда можно представить себе, что часть жидкости отвердела – равновесие оставшейся части жидкости от этого не нарушится. Так, в цилиндрических сообщающихся сосудах мы можем мысленно выделить часть жидкости, которая заполняла бы сообщающиеся сосуды любой извилистой формы (см. рис. 4), и представить себе, что остальная часть жидкости отвердевает. Тогда равновесие выделенной нами части жидкости не нарушится, и, следовательно, уровни жидкости в извилистых сообщающихся сосудах будут такими же, какими были в цилиндрических сосудах, т.е. одинаковыми.
Закон сообщающихся сосудов справедлив только для однородной жидкости. Если в сосуды налиты жидкости разных плотностей, то уровни в сосудах могут быть разными.
Задача 4. В U – образную трубку налита ртуть. Поверх ртути в одно из колен трубки налили воду (рис. 5, a). Высота столбика воды l = 0,1 м. Определите разность уровней жидкостей в коленах трубки. Нарисуйте график зависимости давления в обоих коленах трубки от высоты. Плотность ртути ρрт = 1,36×104 кг/м3, плотность воды ρрт = 103 кг/м3. Атмосферное давление не учитывайте.
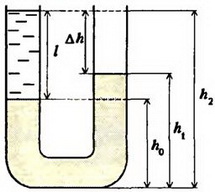
а
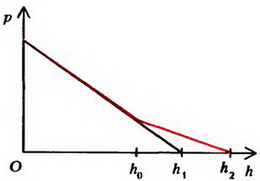
б
Рис. 5
Давления на ртуть на уровне ho соприкосновения воды и ртути в обоих коленах должны быть одинаковы (закон сообщающихся сосудов для однородной жидкости). Поэтому
где разность уровней h2 – h1 обозначена через Δh. Отсюда
Давление в колене, содержащем только ртуть, меняется с высотой h по закону
Эта формула справедлива и в изогнутой части трубки. (Представите себе, что изогнутое колено сообщается с прямым цилиндрическим сосудом, в котором тоже находится ртуть. Тогда давления на одинаковой высоте в обоих сосудах должны быть равны). В другом колене в области , где находится только вода, давление
Ниже уровня h0 зависимость давления от высоты дается той же формулой, что и в первом колене:
Зависимость давления в коленах трубки от высоты изображена графически на рисунке 5, б. Как видно, выше уровня h0 давления на одинаковой высоте разные.
Выталкивающая сила
На тело, погруженное в жидкость, как известно, действует выталкивающая сила. Эта сила является равнодействующей сил давления жидкости на тело. Найдем, например, выталкивающую силу, действующую на кубик с ребром a целиком погруженный в жидкость плотностью ρ. Сила давления со стороны жидкости на верхнюю грань кубика равна
где h – расстояние от этой грани до поверхности жидкости (для простоты мы считаем, что плоскость верхней грани кубика параллельна поверхности жидкости). На нижнюю грань кубика действует сила
Силы давления на боковые грани кубика уравновешивают друг друга. Равнодействующая сил давлении, т.е. выталкивающая сила, равна
и направлена вертикально вверх. Мы получили закон Архимеда: выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость.
В общем случае закон Архимеда можно доказать с помощью принципа отвердевания. Мысленно заменим погруженное тело жидкостью. Очевидно, что эта жидкость будет находиться в равновесии. Следовательно, сила тяжести, действующая на нее, уравновешена силами давления со стороны окружающей жидкости. Если теперь представить себе, что выделенная нами часть отвердела, то равновесие оставшейся части не нарушится, и поэтому не изменятся силы давления на отвердевшую жидкость. Равнодействующая этих сил будет по-прежнему равна силе тяжести.
При доказательстве мы считали, что тело целиком погружено в жидкость. Однако аналогичные рассуждения легко провести и в случае, когда только часть тела находится в жидкости (проделайте это сами). И мы опять получим, что выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость:
где ρ – плотность жидкости, V – объем погруженной в жидкость части тела, g -ускорение свободного падения.
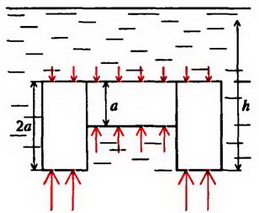
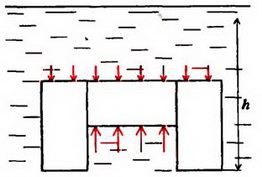
Задача 5. На дне водоема установлена П – образная конструкция из трех одинаковых балок, соединенных между собой (рис. 6). Как зависит сила давления этой конструкции на дно от уровня воды в водоеме? Рассмотрите два случая: 1) вода подтекает под опоры; 2) опоры плотно соприкасаются с дном. Балки имеют квадратное сечение со стороной a, длина балки l = 2a. Плотность материала балок ρ0. плотность воды ρ.
а
б
в
Рис. 6
Сила давления Fд на дно определяется разностью силы тяжести конструкции и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:
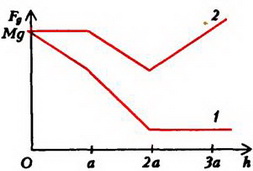
Соответствующий график для силы Fд изображен на рисунке 6, в – он обозначен цифрой 1.
Во втором случае отсутствует давление воды на опоры снизу (рис.6, б), и пользоваться законом Архимеда уже нельзя. Для определения силы F необходимо найти равнодействующую сил давления:
F = 0 при h ≤ a,
Последнее выражение обращается в нуль при и при больших h становится отрицательным. Это означает, что при силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.
Задача 6. Пробковый кубик с ребром a = 0,1 м погрузили в воду на глубину h = 0,2 м с помощью тонкостенной трубки диаметром d = 0,05 м (рис. 7). Определите, какой груз надо положить в трубку, чтобы кубик от нее оторвался. Плотность пробки ρ0 = 200 кг/м3, плотность воды ρ = 103 кг/м3.
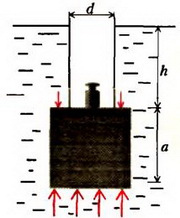
Рис. 7
Вес груза равен разности выталкивающей силы F действующей на кубик, и силы тяжести кубика . Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила . В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:
где – площадь сечения трубки. Таким образом, сила тяжести грузика
Масса грузика т = 1,2 кг.
Выталкивающую силу, действующую на кубик, можно найти и другим способом. Рассмотрим кубик с трубкой как единое тело, вытесняющее объем воды
Тогда по закону Архимеда на кубик с трубкой действует выталкивающая сила
которая равна выталкивающей силе, действующей на кубик, так как равнодействующая сил давления воды на трубку равна нулю.
Жидкость в движущемся сосуде
Изучим теперь равновесие жидкости в сосуде, движущемся с ускорением. По второму закону Ньютона в этом случае векторная сумма всех сил, действующих на любой выделенный элемент жидкости, должна равняться , где m – масса выделенной жидкости, – ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна .
Задача 7. Сосуд с жидкостью плотностью ρ падает с ускорением a. Определите давление жидкости на глубине h и силу давления на дно сосуда. Высота уровня воды в сосуде H, площадь дна сосуда s.
Выделим столбик жидкости высотой h с площадью основания s. На него действуют сила тяжести и сила давления , направленная вверх. Равнодействующая этик сил создает ускорение столбика:
где – масса столбика. Для давления p на глубине h отсюда находим
Сила давления на дно сосуда
будет тем меньше, чем больше ускорение сосуда a. При (свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.
Задача 8. На дне сосуда с жидкостью лежит тело. Может ли тело всплыть, если сосуд начнет двигаться вверх с ускорением? Определите силу давления тела на дно сосуда, если ускорение сосуда a, плотность жидкости ρ0, плотность тела ρ, его объем V.
На тело, лежащее на дне сосуда, действуют сила тяжести mg сила реакции дна N и выталкивающая сила F (рис. 8). Если сосуд покоится, то сумма этих сил равняется нулю. При движении сосуда с ускорением a вверх по второму закону Ньютона имеем
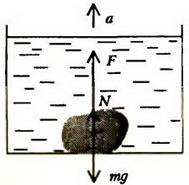
Рис. 8
Определим выталкивающую силу F. Аналогично решению предыдущей задачи, легко получить, что при ускоренном движении сосуда, вверх давление на глубине h дается формулой
т.е. давление в раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:
где – масса вытесненной телом воды.
Подставляя это выражение в формулу второго закона Ньютона, для силы реакции дна получаем
Легко видеть, что в сосуде, движущемся с ускорением вверх, сила реакции дна всегда больше, чем в неподвижном. Поэтому тело не только не всплывает, а наоборот, сильнее прижимается ко дну.
Задача 9. Сосуд с жидкостью движется горизонтально с ускорением a. Определите форму поверхности жидкости в сосуде.
Выделим горизонтальный столбик жидкости длиной l и площадью поперечного сечения S (рис. 9). По второму закону Ньютона
где – масса столбика, p1 и p2 – давления на него слева и справа.
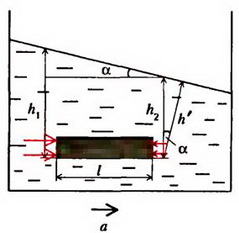
Рис. 9
Давление на глубине h определяется по обычной формуле (по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем
или
Но – это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем .
Заметим, что давление жидкости на данной высоте здесь не одно и то же. Линии равного давления параллельны поверхности жидкости. Если ввести расстояние h´ от точки до поверхности жидкости, то давление в этой точке
Поэтому можно сказать, что ускоренное движение сосуда эквивалентно замене ускорения свободного падения на величину . Это утверждение в равной степени относится и к предыдущим двум задачам.
Упражнения
1. Три сосуда, имеющие формы цилиндра, усеченного конуса и перевернутого усеченного конус с одинаковыми площадями оснований и рапными объемами, доверху наполнены водой. Как соотносятся между собой силы давлении воды на дно сосудов?
2. Трубка ртутного барометра подвешена нити. Определите натяжение нити, если высота уровня ртути и трубке Н = 0,76 м, внешний диаметр трубки D = 0,02 м, внутренний d = 0,017 м. нижний конец трубки погружен в ртуть на глубину h = 0,1 м, масса трубки m = 0,3 кг, плотность ртути ρ = 1,36×104 кг/м4. Считайте, что торцы трубки плоские.
3. Длинная вертикальная трубка погружена одним концом в сосуд с ртутью. В трубку наливают m = 0,71 кг воды, которая не вытекает из трубки. Определите изменение уровня ртути и сосуде. Диаметр сосуда D = 0,06 м, плотность ртути ρ = 1,36×104 кг/м4. Толщиной стоим трубки пренебречь.
4. В сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лед растает? Что будет, если в лед вморожен а) кусочек свинца: б) кусочек пробки?
5. В цилиндрические сообщающиеся сосуды диаметрами D = 0,06 м и d = 0,02 м налита вода. Как изменятся уровни воды в сосудах, если в один из сосудов поместить тело массой т = 0,02 кг, которое будет плавать в воде? Плотность воды ρ = 103 кг/м3.
6. Сосуд с водой скользит без трения по наклонной плоскости с углом наклона α. Определите, как расположится поверхность воды и сосуде.
Ответы
1. Сила давления на дно наибольшая у сосуда, имеющего форму усеченного конуса, наименьшая – у перевернутого конуса.
2.
3.
4. Если лед чистый или в него вморожен кусочек пробки, то уровень воды не изменится. Если же в лед вморожен кусочек свинца, уровень воды понизится.
5.
6. Поверхность параллельна наклонной плоскости.
Источник
