В цилиндрический сосуд доверху наполненный водой опустили шарик
#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
1.338. На столе стоит цилиндрический сосуд высоты H, наполненный доверху водой. Пренебрегая вязкостью воды, определить высоту h, на которой нужно сделать в сосуде небольшое отверстие, чтобы вытекающая из него струя попадала на стол на наибольшем удалении от сосуда.
1.339. Цилиндрический сосуд высоты h=0,500 м и радиуса R=10,0 см наполнен доверху водой. В дне сосуда открывается отверстие радиуса r=1,00 мм. Пренебрегая вязкостью воды, определить: а) время τ, за которое вся вода вытечет из сосуда, б) скорость v перемещения уровня воды в сосуде в зависимости от времени.
1.340. Шприц, применяемый для заправки смазкой шарнирных соединений автомобиля, заполнили для промывки керосином. Радиус поршня шприца R=2,00 см, ход поршня l = 25,0 см. Радиус выходного отверстия шприца r = 2,00 мм. Пренебрегая вязкостью керосина и трением поршня о стенки, определить время τ, за которое будет вытеснен керосин из шприца, если давить на поршень с постоянной силой F = 5,00 Н. Плотность керосина ρ принять равной 0,800 г/см3.
1.341. С мостика, переброшенного через канал, по которому течет вода, опущена узкая изогнутая трубка, обращенная открытым концом навстречу течению (рис. 1.51). Вода в трубке поднимается на высоту h=150 мм над уровнем воды в канале. Определить скорость v течения воды.
1.342. Устройство, называемое трубкой Пито-Прандтля, состоит из двух узких коаксиальных трубок (рис. 1.52). Внутренняя трубка открыта на нижнем конце, внешняя имеет боковые отверстия. Верхние концы трубок подключены к дифференциальному манометру (т. е. манометру, показывающему разность давлений Δр). С помощью этого устройства можно измерять скорость жидкости (или газа). Для этого его погружают в жидкость, обратив открытым концом навстречу потоку, и отсчитывают Δр. При погружении трубки в поток жидкости с плотностью ρ=1,10*103 кг/м3 была обнаружена разность давлений Δp=4,95*103 Па. Найти скорость v течения жидкости.
1.343. По горизонтальной трубе радиуса R=12,5 мм течет вода. Поток воды через сечение трубы Q=3,00*10-5 м3/с. Определить: а) характер течения, б) перепад давления на единицу длины трубы dp/dl. Вязкость воды принять равной η=1,00*10-3 Па*с.
1.344. Два одинаковых цилиндрических бака соединены узкой трубкой с краном посредине (рис. 1.53). Радиус баков R=20,0 см, радиус трубки r=1,00 мм. Длина трубки l=1,00 м. Проходное отверстие крана совпадает с сечением трубки. В один из баков налита вода до высоты h=50,0 см, второй бак вначале пустой. В момент t=0 кран открывают. Определить: а) характер течения воды в трубке в первые секунды, б) время τ, по истечении которого разность уровней воды в баках уменьшается в е раз. Вязкость воды принять равной η=1,00*10-3 Па*с.
1.345. Над нагретым участком поверхности Земли установился стационарный поток воздуха, направленный вертикально вверх и имеющий скорость u=20,0 см/с. В потоке находится шаровидная пылинка, которая движется вверх с установившейся скоростью v=4,0 см/с. Плотность пылинки ρ=5,00*103 кг/м3, плотность воздуха ρ0=1,29 кг/м3. Вязкость воздуха η=1,72*10-5 Па*с. а) Определить радиус пылинки r. б) Убедиться в том, что обтекание пылинки воздухом имеет ламинарный характер. Примечание. Для шарика критическое значение числа Рейнольдса Re (т. е. значение, при котором ламинарное обтекание шарика переходит в турбулентное) равно 0,250, если в качестве характерного размера принять радиус шарика.
1.346. В высокий широкий сосуд налит глицерин (плотность ρ0=1,21*103 кг/м3, вязкость η=0,350 Па*с). В глицерин погружают вдалеке от стенок сосуда и отпускают без толчка шарик радиуса r=1,00 мм. Плотность шарика ρ=10,0*103 кг/м3. Первоначальная высота шарика над дном сосуда h=0,500 м. а) Определить, можно ли силу сопротивления движению шарика вычислять по формуле Стокса (см. примечание к задаче 1.345). б) Найти зависимость пути s, пройденного шариком, от времени t. в) Найти время τ, за которое шарик достигнет дна сосуда. г) Определить время t, по истечении которого скорость шарика будет отличаться от предельного значения v0, не более чем на 1 %.
Источник
Основы гидродинамики
Для успешного решения задания № 5 требуется знание основ гидродинамики. К ним относится понимание процессов, происходящих с жидкостями и телами, контактирующими с жидкостями, сущности физ.величин плотности и давления, а также формул, связывающих их с другими физ.величинами. Необходимая для решения задач такого плана информация имеется в разделе теории.
Теория к заданию №5 ОГЭ по физике
Плотность вещества
Плотностью называют массу вещества, которая приходится на единицу объема. Следовательно, плотностью можно считать удельную массу вещества. Количественно плотность определяют по формуле:
где m – массе вещества, V – его объем.
По этой же формуле вычисляется и средняя плотность. Для расчета при этом берется масса всего вещества и его общий объем.
Давление
Давлением называется: 1) сила, которая воздействует на поверхность твердого тела; 2) степень (сила) упругости жидкости либо газа. По сути, давление – это мера механического напряжения. Эта физ.величина является скалярной.
Давление в физике традиционно обозначается лат.буквой р. Единица измерения давления – паскаль (Па).
Атмосферное давление – это сила воздействия атмосф.столба на все физ.объекты (тела), находящиеся в атмосфере Земли, а также на земную поверхность. Если атмосфера является стационарной и покоящейся, то атмосф.давление на материальный объект соответствует весу столба воздуха над этим объектом, приходящегося на единицу площади. Атмосф.давление измеряется в мм ртутного столба (мм рт.ст.). Нормальным принято давление в 760 мм рт. ст. при t=0ºC. В пересчете на единицы СИ это давление соответствует 101325Па.
Сила Архимеда
На помещенное в жидкость физ.тело воздействует выталкивающая сила, равная по величине силе тяжести, испытываемая этим телом. Причина возникновения архимедовой силы – неодинаковость гидростатического давления в жидкости на различных глубинах. Точка ее приложения называется центром давления, который является центром масс тела (или его части) погруженного в жидкость
Формула для вычисления силы Архимеда:
где ρж – плотность жидкости; V – объем части физ.тела, помещенной в жидкость, или всего тела, если оно погружено в жидкость полностью.
Сообщающиеся сосуды
Сообщающимися считаются сосуды, которые объединены ниже поверхности жидкости в единую систему, причем так, что жидкость может перетекать из одного в другой.
Закон сообщающихся сосудов:
что означает обратную пропорциональную зависимость высоты столбов жидкостей и их плотностей.
Если в сообщающихся сосудах находится жидкость однородная, то высота столбов свободной поверхности жидкости в них совпадает.
Разбор типовых вариантов заданий №5 ОГЭ по физике
Демонстрационный вариант 2018
Цилиндр 1 поочередно взвешивают с цилиндром 2 такого же объема, а затем с цилиндром 3, имеющим меньший объем (см. рисунок).
Максимальную среднюю плотность имеет цилиндр
- 1
- 2
- 3
- 1 и 3
Алгоритм решения:
- Анализируем условие и рисунок слева (цилиндры 1 и 2). Определяем соотношение плотностей цилиндров.
- Анализируем условие и рисунок справа (цилиндры 3 и 1). Делаем вывод относительно соотношения плотностей.
- Определяем цилиндр с максимальной плотностью.
Решение:
- Согласно условию: . Поскольку на весах слева цилиндр 1 перевешивает 2, то это значит, что . Тогда из уравнения следует, что .
- По условию . Поскольку весы справа уравновешены, то это значит, что массы цилиндров равны, и из уравнения для плотности следует: .
- Объединив неравенства (1) и (2), получим: . Отсюда: максимальная плотность у 3-го цилиндра.
Ответ: 3
Первый вариант (Камзеева, № 7)
Одно из колен U-образного манометра соединили с сосудом, наполненным газом (см. рис.). Атмосферное давление равно 760 мм рт.ст. Чему равно давление газа в сосуде? В качестве жидкости в манометре используется ртуть.
- 1160 мм рт.ст
- 500 мм рт.ст.
- 360 мм рт.ст.
- 100 рт.ст.
Алгоритм решения:
- Анализируем условие и рисунок. Делаем вывод о соотношении атмосф.давления и давления в сообщающихся сосудах.
- Определяем искомую величину давления газа.
- Фиксируем ответ.
Решение:
- На схеме показано, что уровень ртути в 1-м (левом) колене меньше, чем в среднем. Это означает, что атмосф.давление выше давления газа. На шкале на рисунке видно, что разница давлений составляет 40 см. рт. ст., то есть 400 мм. рт. ст.
- Имеющаяся разница давлений означает, что давление газа меньше на эту разницу по сравнению с атмосферным давлением, т.е.: p = 760 — 400 = 360 (мм. рт. ст.).
Ответ: 3
Второй вариант (Камзеева, № 10)
Имеются три сплошных шара одинаковой массы, но изготовленные из разных веществ – из алюминия, стали или свинца. Шары полностью погружают в воду. Выталкивающая сила со стороны воду имеет
- наибольшее значение для алюминиевого шара
- наибольшее значение для стального шара
- наибольшее значение для свинцового шара
- одинаковое значение для всех шаров
Алгоритм решения:
- Записываем табличные значения для плотности материалов шаров.
- Записываем уравнение з-на Архимеда.
- Анализируем уравнение и определяем соотношение для выталкивающей силы для шаров.
- Записываем ответ.
Решение:
- Плотности материалов шаров: ; ; .
- Согласно з-ну Архимеда, выталкивающая сила равна: . Поскольку по условию шары погружены в жидкость целиком, то V – полный объем шара.
- Т.к. во всех 3 случаях жидкость одна и та же (вода), то в уравнении совпадает для всех шаров. Соответственно, максимальная архимедова сила у того из них, который имеет наибольший объем. Объем выразим из формулы для плотности вещества: . Учитывая оговорку в условии о том, что у шаров одинаковая масса, делаем вывод: чем меньше плотность вещества шара, тем больше выталкивающая сила. Поскольку наименьшую плотность имеет алюминий, то именно на алюминиевый шар действует максимальная выталкивающая сила.
Ответ: 1
Третий вариант (Камзеева, № 12)
Сосуд частично заполнили водой и уравновесили на рычажных весах (см. рис.).
В первом случае в сосуд опустили пробковый шарик, во втором случае – стальной шарик. Нарушится ли равновесие весов?
- равновесие нарушится только в первом случае
- равновесие нарушится только во втором случае
- равновесие нарушится в обоих случаях
- в обоих случаях равновесие не нарушится
Алгоритм решения:
- Анализируем 1-й случай. Делаем вывод о положении весов.
- Анализируем 2-й случай. Делаем вывод о положении весов.
- Находим верный вариант ответа. Записываем его.
Решение:
- В 1-м случае – с пробковым шариком – шарик будет плавать на поверхности воды (т.к. пробковый материал легче воды). При этом, поскольку сосуд заполнен водой целиком, при опускании в нее шарика она по з-ну Архимеда частично выплеснется. Сила тяжести, действующая на шарик, равна весу выплеснувшейся воды, так что вес шарика компенсирует ее. Поэтому равновесие весов сохранится.
- Масса стального шарика больше, чем масса воды, которую он выплеснет из сосуда, погрузившись в нее. Это означает, сила тяжести больше веса выплеснувшейся воды, и под действием результирующей этих сил равновесие будет нарушено.
- Ситуация, при которой в 1-м случае равновесие не нарушается, а во 2-м нарушается, соответствует варианту ответа 2
Ответ: 2
Даниил Романович | ???? Скачать PDF |
Источник
5. Механика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке представлены графики зависимости давления (p) от глубины погружения (h) для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре. 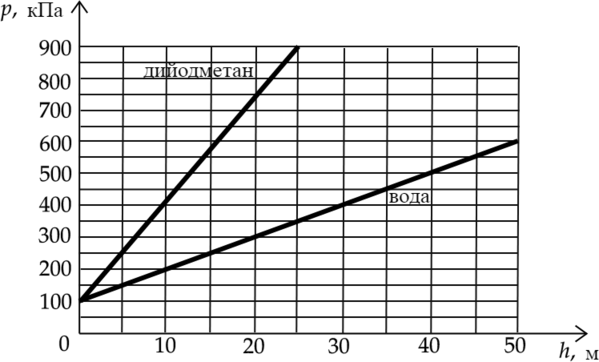
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
2) Плотность керосина 0,82 г/см(^3), аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
3) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
4) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
5) Плотность оливкового масла 0,92 г/см(^3), аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Полное давление (p) складывается из атмосферного давления (p_a) и гидростатического давления столба жидкости: [p=rho gh+p_a] 1) Как видно из графика, давление воды на глубине 10 м принимает значение 200 кПа, что в два раза больше атмосферного давления (Атмосферное давление 100 кПа).
Утверждение 1 – (color{red}{small text{Неверно}})
2) Так как плотность керосина меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 2 – (color{red}{small text{Неверно}})
3) Давление в воде на глубине 25 м равно 350 кПа, что в 3,5 раза больше атмосферного.
Утверждение 3 – (color{red}{small text{Неверно}})
4) Так как прямая давления в дийодметане лежит выше прямой давления в воде, то это означает, что давление в дийодметане возрастает быстрее, чем в воде.
Утверждение 4 – (color{green}{small text{Верно}})
5) Так как плотность оливкого масла меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 45
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см(^3), плотность жидкости 800 кг/м(^3), объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.
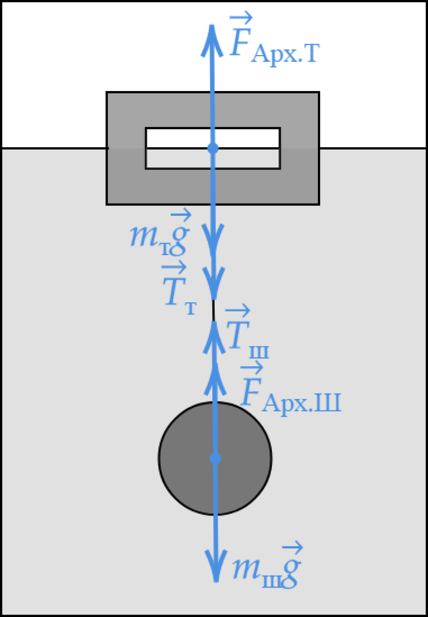
Запишем первый закон Ньютона для тела и шарика: [F_{text{Арх Т}}-m_{text{Т}}g-T=0] [F_{text{Арх Ш}}-m_{text{Ш}}g+T=0]
Сложим два уравнения: [F_{text{Арх Т}}-m_{text{Т}}g+F_{text{Арх Ш}}-m_{text{Ш}}g=0]
Обозначим плотность жидкости (rho_1), плотность материала (rho_2=2rho_1) [rho_1gV_1-rho_2cdot frac{1}{4}V_{T} g+rho_1 g cdot frac{1}{4} V_{T}-rho_2cdot frac{1}{4} V_{T} g=0] [rho_1V_1-2rho_1cdot frac{1}{4}V_{T} +rho_1 cdot frac{1}{4} V_{T}-2rho_1cdot frac{1}{4} V_{T} =0] [V_1-2cdot frac{1}{4}V_{T} + frac{1}{4} V_{T}-2cdot frac{1}{4} V_{T} =0] [V_1=frac{3}{4}V_T]
Тело плавает, погруженное на 3/4 своего объёма.
1) Сила Архимеда, действующая на тело, равна (displaystyle F_{text{Арх Т}}=rho_1gfrac{3}{4}V_T), а сила Архимеда, действующая на шар (displaystyle F_{text{Арх Т}}=rho_1gfrac{1}{4}V_T).
Утверждение 1 – (color{red}{small text{Неверно}})
2) [T=m_{text{Ш}}g-F_{text{Арх Ш}}]
Утверждение 2 – (color{red}{small text{Неверно}})
3) [T=F_{text{Арх Т}}-m_{text{Т}}g]
Утверждение 3 – (color{green}{small text{Верно}})
4) Модуль силы тяжести тела:[m_{text{Т}}g=rho_2cdot frac{1}{4}V_{T}g] Модуль силы тяжести шарика: [m_{text{Ш}}g=rho_2cdot frac{1}{4}V_{T}g]
Утверждение 4 – (color{green}{small text{Верно}})
5) Объём погружённой части тела равен (dfrac{3}{4}) объёма этого тела.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 34
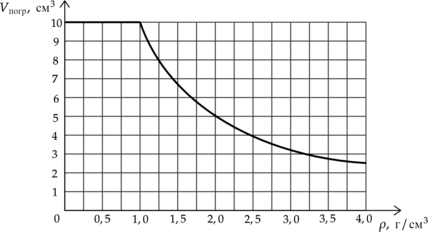
Ученик помещал цилиндр, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погруженной в жидкость части цилиндра (V_text{ погр}). По результатам измерений он получил зависимость, представленную на графике объема погруженной части цилиндра (V_text{погр}) от плотности жидкости (rho). Объем цилиндра постоянен и равен (V=10) см(^3)
 [begin{array}{|c|c|c|c|c|c|c|c|}
[begin{array}{|c|c|c|c|c|c|c|c|}
hline
text{Жидкость}&text{Бензин}&text{Спирт}&text{Вода}&text{Глицирин}&text{Хлороформ}&text{Бромоформ}&text{Дийодметан}\
hline
text{Плотность $rho$ г/см$^3$}&0,71&0,79&1,0&1,26&1,49&2,89&3,25\
hline
end{array}]
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) В бензине и воде сила Архимеда, действующая на цилиндр, одинакова.
2) Цилиндр не тонет в глицерине.
3) На цилиндр, погруженный в бромоформ, действует сила Архимеда 200мН.
4) Цилиндр плавает во всех жидкостях, указанных в таблице.
5) При плавании цилиндра в глицирине и бромоформе сила Архимеда, действующая на него, одинакова.
1) В бензине и в спирте цилиндр погружен на одинаковый объем. В таком случае сила Архимеда равна [F_A=rho gV_text{погр},] где (rho) – плотность жидкости, в которую погружено тело.
Но плотность спирта больше плотности бензина, а значит и сила Архимеда, действущая на цилиндр в спирте, больше силы Архимеда, действующей на цилиндр в бензине.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Цилиндр тонет при плотности меньше, чем 1 г/см(^3), у глицирина плотность 1,26 г/см(^3), значит, цилиндр плавает.
Утверждение 2 – (color{green}{small text{Верно}})
3) У бромоформа плотность больше 1 г/см(^3), а значит сила Архимеда уравновешивает силу тяжести.
По графику видим, что цилиндр начинает плавать при плотности жидкости 1г/см(^3), а значит именно такова плотность материала, из которого он сделан. Откуда сила Архимеда, действующая на цилиндр [F_A=mg=1text{ г/см$^3$}cdot 10text{ см$^3$}cdot 10text{ Н/кг}=100text{ мН}] Утверждение 3 – (color{red}{small text{Неверно}})
4) Нет, при плотности меньше 1 г/см3 цилиндр не плавает.
Утверждение 4 – (color{red}{small text{Неверно}})
5) У глицирина и бромоформа плотность больше 1 г/см(^3), а значит сила Архимеда уравновешивает силу тяжести и силы Архимеда одинаковы.
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 25
На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок). 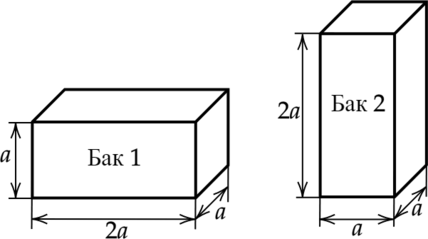
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление воды на дно первого бака в 4 раза меньше, чем на дно второго.
2) Первый бак давит на пол лифта с силой, в 2 раза меньшей, чем второй.
3) Сила давления воды на дно первого бака в 2 раза меньше, чем на дно второго.
4) Первый бак оказывает на пол лифта в 2 раза меньшее давление, чем второй.
5) Если лифт начнёт движение вниз с ускорением 2 м/с(^2), давление воды на дно баков уменьшится на 20 %.
1) Давление воды на дно первого бака равно [displaystyle p_1=frac{mg}{2a^2}] где (m) — масса воды. Давление на дно второго бака [displaystyle p_2=frac{mg}{a^2}] Видно, что давление (p_2=2p_1), следовательно, давление воды на дно первого бака в 2 раза меньше, чем на дно второго бака.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Сила давления равна силе тяжести воды. Так как объем одинаковый, значит масса воды в сосудах одинаковая.
Утверждение 2 – (color{red}{small text{Неверно}})
3) Утверждение 3 – (color{red}{small text{Неверно}})
4) Утверждение 4 – (color{green}{small text{Верно}})
5) При движении лифта вниз с ускорением 2 м/с(^2), оно будет компенсировать ускорение свободного падения (g), то есть вода будет иметь ускорение свободного падения 10-2=8 м/с(^2). В результате сила давления на дно баков будет равна (F=8m).
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 45
В сосуд с жидкостью погружают маленький датчик манометра, который регистрирует давление, создаваемое только столбом жидкости (без учёта атмосферного давления). На рисунке представлен график зависимости показаний (p) этого датчика давления от времени (t). Известно, что датчик может либо двигаться строго по вертикали вниз со скоростью 1 мм/с, либо покоиться. 
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) Максимальная глубина погружения датчика давления равна 20 см.
2) В промежутке времени от 50 с до 150 с датчик давления находился на одной и той же глубине.
3) Плотность жидкости, в которую опустили датчик давления, равна 650 кг/м(^3).
4) Максимальная глубина погружения датчика давления равна 15 см.
5) Плотность жидкости, в которую опустили датчик давления, равна 1300 кг/м(^3).
1) Датчик двигался на промежутках от 0 с до 50 с и от 150 с до 200 с, т. е. глубина погружения (h=1 cdot (50 + 50 ) = 100) мм(= 10) см.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Из графика видно, что давление не изменяется в промежутке времени от 50 с до 150 с, это означает что датчик находился на одной и той же глубине, т. е. покоился.
Утверждение 2 – (color{green}{small text{Верно}})
3) Давление столба жидкости: [p=rho gh] Плотность жидкости: [rho=frac{p}{gh}=frac{p}{gupsilon t}=frac{650}{10cdot0,001cdot50}=1300 text{ кг/м$^3$}]
Утверждение 3 – (color{red}{small text{Неверно}})
4) Глубина погружения 10 см
Утверждение 4 – (color{red}{small text{Неверно}})
5) Плотность жидкости (rho=1300) кг/м(^3)
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 25
Источник
