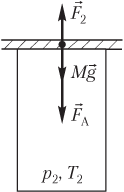В цилиндрическом сосуде с газом находится в равновесии
2017-10-05
Расположенный горизонтально цилиндрический сосуд, заполненный идеальным газом, разделен поршнем, который может двигаться без трения. В равновесии поршень находится посредине цилиндра. При малых смещениях из положения равновесия поршень совершает колебания. Найти зависимость частоты этих колебаний от температуры, считая процесс изотермическим.
Решение:
В положении равновесия давление $p$ на поршень слева и справа одинаково. Поскольку объем газа слева и справа одинаков, а температура $T$ постоянна, из уравнения Менделеева — Клапейрона
$pV = nu RT$ (1)
следует, что количество газа $nu$ одинаково по обе стороны от поршня. Отметим, что химический состав газов может быть различным.

рис.1
Пусть поршень сместился из положения равновесия, например влево, на малую величину $x$, так что $Sx ll V$, где $S$ — площадь поршня (рис. 1). Поскольку температура по условию не меняется, то
$(p + Delta p_{1})(V – Sx) = (p – Delta p_{2}) (V + Sx)$.
Раскрыв скобки и приведя подобные члены, получим
$( Delta p_{1} + Delta p_{2}) V – ( Delta p_{1} – Delta p_{2}) Sx = 2pSx$.
Второе слагаемое слева много меньше первого не только потому, что $Sx ll V$, но и вследствие того, что множителем при $V$ стоит сумма двух близких величин $Delta p_{1}$ и $Delta p_{2}$, а множителем при $Sx$ — их разность. Пренебрегая вторым слагаемым, получаем
$Delta p_{1} + Delta p_{2} = frac{2pS}{V} x$.
Результирующая сила, действующая на поршень, равна
$F = – frac{2pS^{2}}{V} x$.
Знак минус означает, что сила направлена в сторону, противоположную направлению смещения поршня, т. е. к положению равновесия. Под действием силы, пропорциональной смещению, поршень массой $M$ будет совершать гармонические колебания с частотой $omega$, определяемой соотношением
$omega^{2} = 2pS^{2}/VM$. (2)
При решении задачи мы молчаливо предполагали, что масса газа много меньше массы поршня, так что кинетической энергией макроскопического движения газа при колебаниях поршня можно пренебречь но сравнению с кинетической энергией поршня. Подумайте, где использовано это условие.
Выразив $p$ из уравнения Менделеева — Клапейрона (1), получим
$omega^{2} = frac{2 nu RS^{2}}{MV^{2}} T$. (3)
Таким образом, частота колебаний поршня пропорциональна $sqrt{T}$, ибо коэффициент при $T$ в формуле (3) не зависит от температуры, если пренебречь тепловым расширением сосуда.
Подумайте теперь, какие условия должны выполняться, чтобы процесс действительно был изотермическим. Для того чтобы температура газа в процессе колебаний не изменялась, необходим хороший тепловой контакт с большим тепловым резервуаром — термостатом, имеющим постоянную температуру. Что значит хороший тепловой контакт? Это значит, что время установления термодинамического равновесия между газом в сосуде и термостатом должно быть много меньше периода колебаний поршня. Тогда можно считать, что газ в каждый момент имеет ту же температуру, что и термостат. Если, наоборот, период колебаний окажется много меньше времени установления термодинамического равновесия между газом и термостатом, то можно считать, что колебания поршня происходят практически без обмена теплотой с термостатом. В этом случае процесс можно считать адиабатическим, несмотря на отсутствие тепловой изоляции сосуда с поршнем. Оказывается, что зависимость частоты колебаний от температуры при этом будет такой же, как и в изотермическом случае, только коэффициент в формуле (3) умножится на число, большее единицы. Увеличение частоты колебаний при адиабатическом процессе можно объяснить, сравнивая $p-V$ – диаграммы изотермического и адиабатического процессов идеального газа.
Отметим, что приведенное решение в обоих случаях имеет смысл, только если время установления теплового равновесия в самом газе много меньше периода колебаний поршня, так как в противном случае вообще теряют смысл такие равновесные макроскопические характеристики газа, как давление и температура. Другими словами, по отношению к самому газу процесс должен быть квазистатическим.
Источник
5.4. Практическое применение уравнения состояния идеального газа
5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем
Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
m = const;
- постоянным остается также количество вещества (газа):
ν = const;
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
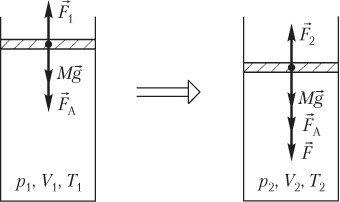
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).
Рис. 5.9
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p1V1=νRT1,p2V2=νRT2,}
где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
Mg+FA=F1,Mg+FA+F=F2,}
где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
T ≠ const;
- если процесс происходит медленно, то температура газа остается постоянной –
T = const.
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
M = 0;
- в остальных случаях поршень обладает определенной ненулевой массой —
M ≠ const.
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.
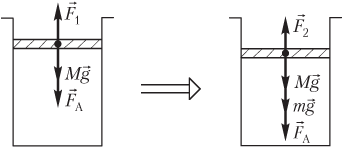
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→1, действующая со стороны газа (до его сжатия);
- сила давления газа F→2, действующая со стороны газа (после его сжатия);
- mg→ — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
F
1 = Mg + F
A,
где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F
2 = Mg + F
A
+ mg,
где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
p
1V
1 = νRT,
где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
p
2V
2 = νRT,
где V
2 — объем сжатого поршнем газа.
Равенство
p
1V
1 = p
2V
2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}
которую требуется решить относительно массы гирь m.
Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:
p2p1=Mg+pAS+mgMg+pAS
и из третьего уравнения:
p2p1=V1V2,
запишем равенство правых частей полученных отношений:
Mg+pAS+mgMg+pAS=V1V2.
Отсюда следует, что искомая масса определяется формулой
m=(M+pASg)(V1V2−1).
Вычисление дает результат:
m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→2, действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
F
2 = Mg + F
A,
где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
p
1V = νRT
1,
где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
p
2V = νRT
2,
где p
2 — давление нагретого газа; T
2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}
систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.
Для этого делением первой пары уравнений
pAVp2V=νRT1νRT2
получим выражение для давления нагретого газа:
p2=pAT2T1
и подставим его в третье уравнение системы:
pAT2ST1=Mg+pAS.
Преобразуем полученное выражение к виду
T2=T1(Mg+pAS)pAS=T1(MgpAS+1),
а затем найдем разность
ΔT=T2−T1=MgT1pAS.
Произведем вычисление:
ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→, действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:
F→+F→A+Mg→=ma→,
или в проекции на вертикальную ось —
F − F
A − Mg = Ma,
где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a=F−FA−MgM=(p−pA)SM−g.
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
l=v22a,
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
v=2al
и подставим в записанную формулу выражение для модуля ускорения:
v=2l((p−pA)SM−g).
Выполним расчет:
v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Источник
1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)
4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
 6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)
6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)
7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)
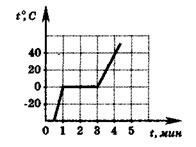 8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)
8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)
9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)
10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)
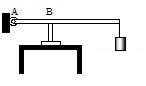
11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)
12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)
13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)
14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.
(Решение)
15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)
16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)
19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)
(Решение)
20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)
21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)
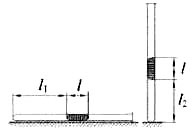 22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)
23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)
24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)
25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)
26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)
27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)
Источник