В цилиндрическом сосуде с площадью дна s в воде плавает кусок льда
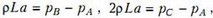
Задачи, тесты
Е. М.
Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5,
8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где  – объём погружённой части коробочки. Подставляя числовые данные, получаем
– объём погружённой части коробочки. Подставляя числовые данные, получаем 
Отсюда глубина погружения коробочки равна

Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:

20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:

23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина 
Решая совместно оба уравнения, получаем:

24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на  Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению:
Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению: 
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле  полученной при решении задачи 9 (см. № 5/2010):
полученной при решении задачи 9 (см. № 5/2010):

– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:

Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:

26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна

Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты
S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
Задача 2.
Ведро, в котором находится m = 10 кг смеси воды со льдом, внесли в комнату и сразу начали измерять температуру смеси. График зависимости температуры от времени t(t) изображен на рисунке. Какая масса льда была в ведре, когда внесли в комнату? Удельная теплоемкость воды с=4200 Дж/(кг оС), удельная теплота плавления льда l = 330 кДж/кг. Теплоемкостью ведра пренебречь.

(10 баллов)
Возможное решение | |
Таяние льда в ведре и нагревание воды происходит за счет теплообмена с окружающей средой. Так как рост температуры от времени в рассматриваемом диапазоне является линейным, то мощность Р теплового потока можно считать постоянной. Уравнение теплового баланса для таяния льда mлl = Рt0, где mл – масса льда в ведре, t0 = 50 мин – время таяния льда. Уравнение теплового баланса при нагревании воды mсΔt = РΔt, где Δt – время нагревания воды. Из графика определим. Таким образом | |
Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин; представлено полное верное объяснение с указанием наблюдаемых явлений и законов: пояснили, что таяние льда в ведре и нагревание воды происходит за счет теплообмена с окружающей; Заметили, что рост температуры от времени в рассматриваемом диапазоне является линейным, следовательно мощность Р теплового потока можно считать постоянной средой записано уравнение теплового баланса для таяния льда mлl = Рt0; уравнение теплового баланса при нагревании воды mсΔt = РΔt; определим проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу; представлен правильный ответ с указанием единиц измерения искомой величины | 1 1 2 1 1 1 2 1 |
Задача 3.
Резисторы сопротивлениями R1 = 1 кОм, R2 = 2 кОм, R3 = 3 кОм, R4 = 4 кОм подключены к источнику постоянного напряжения U0 = 33В через клеммы А и В. К резисторам подключили два идеальных амперметра А1, А2. Определите показания амперметров I1, I2.

(10 баллов).
Возможное решение | |
Определим токи Ii, текущие через резисторы Ri (i = 1, 2, 3, 4). Так как амперметры идеальные, то можно рассмотреть эквивалентную электрическую цепь. Для этой цепи , RAB = RAC + RCB = . Полный ток в цепи Для определения показания амперметров запишем закон сохранения токов в узлах d и с ( выбранное направление токов указано на рисунке): I1 = IR1 – IR3 = 5 мА, I2 = IR3 – IR4 = 4 мА
| |
Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: Сделан пояснительный рисунок; проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу определили сопротивление RAC; определили сопротивление RCB; определили сопротивление RAB; | 1 1 1 1 |
определили I; определили IR1; определили IR2; определили IR3; представлен правильный ответ с указанием единиц измерения искомой величины : I1 = 5 мА, I2 = 4 мА | 1 1 1 1 2 |
Задача 4.
Кусок льда привязан нитью ко дну цилиндрического сосуда с водой (см. рис.). Над поверхностью воды находится некоторый объём льда. Нить натянута с силой Т= 1Н. На сколько и как изменится уровень воды в сосуде, если лёд растает? Площадь дна сосуда S= 400 см2 , плотность воды ρ= 1 г/см3.

(10 баллов)
Возможное решение | |
Запишем условие плавания куска льда в воде: mлg+ Т =FА= ρ вVп.ч.g; где Vп.ч – объём погружённой в воду части куска льда. Найдём первоначальный уровень воды в сосуде (1), где V о – первоначальный объём воды в сосуде до таяния льда. Соответственно (2), где h2 – уровень воды в сосуде, после таяния льда, V 1 – объём воды, полученной из льда. Решая совместно (1) и (2), получаем h 1 –h 2 = (V п.ч. –V1 )/S; найдём Vп.ч = (m лg+Т)/( ρ в.g). Учтём mл = m1, где m1 – масса воды, полученной изо льда m1 = ρвV1 ; V1 = mл/ρв. Тогда h 1 –h 2 = ((mлg+Т)/ ρ вg. – m л / ρ в )/ S = 2,5 мм | |
Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: cделан пояснительный рисунок, с указанием всех действующих сил; описаны все вновь вводимые в решении буквенные обозначения физических величин; представлено полное верное объяснение с указанием наблюдаемых явлений и законов: записано условие плавания куска льда в воде: mлg + Т = FА= ρвVп.ч.g; записали формулу для расчета h1 ; записали формулу для расчета h2; проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: h 1 –h 2 = (V п.ч. –V1 )/S; Vп.ч = (mлg+Т)/(ρв.g); V1 = mл/ρв ; h 1 –h 2 = ((mлg+Т)/ ρ вg. – m л / ρ в )/ S. Представлен правильный ответ с указанием единиц измерения искомой величины: h 1 –h 2 = 2,5 мм | 1 1 1 1 1 1 1 1 1 1 |
Задача 5.
Чему должен быть равен минимальный коэффициент трения μ между шинами и поверхностью наклонной дороги с уклоном α=30о, чтобы автомобиль мог двигаться по ней вверх с ускорением a=0,6 м/с2?
(10 баллов)
Возможное решение | |
Cилой, вынуждающей двигаться автомобиль является сила трения покоя F(тр.п)макс . Проскальзыванием колёс и силой трения качения пренебрегаем. Укажем все действующие на автомобиль силы и запишем 2 закон Ньютона ma = Fтр.п. + mg. Через проекцию на ось ОХ: Fтр.п. – mg = ma Fтр.п.=μN; OY: N = mg Þ Fтр.п.=μ mg Þ μmg – mg = ma ; μ = (а + g)/g ; μ = 0,64. | |
Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: cделан пояснительный рисунок, с указанием всех действующих сил; представлено полное верное объяснение с указанием наблюдаемых явлений и законов (II закон Ньютона); cилой, вынуждающей двигаться автомобиль является сила трения покоя F(тр.п)макс; Проскальзыванием колёс и силой трения качения пренебрегаем; проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: ОХ: Fтр.п. – mg = ma OY: N = mg μmg – mg = ma μ = (а + g)/g Представлен правильный ответ с указанием единиц измерения искомой величины: μ = 0,64 | 2 1 1 1 1 1 1 1 1 |
| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 |
Источник
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
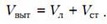
Очевидно, что этот же объем равен
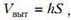
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
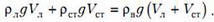
Из совместного решения полученных уравнений найдем объемы льда и стекла:
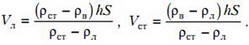
Из растаявшего льда образовалась вода объемом
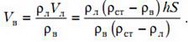
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
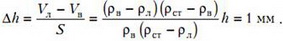
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
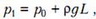
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
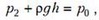
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
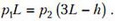
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
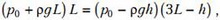
или, если записать атмосферное давление в виде , где H0 = 774 мм:
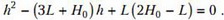
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
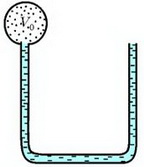
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
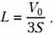
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
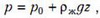
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
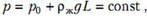
а на третьем участке, для
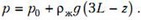
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
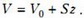
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
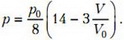
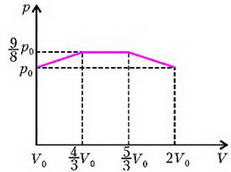
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
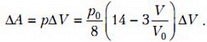
Запишем уравнение состояния гелия как идеального газа:
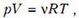
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
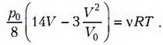
Продифференцируем обе части этого уравнения:
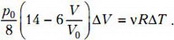
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
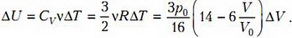
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
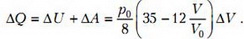
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
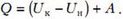
Поскольку начальная и конечная температуры равны, соответственно,
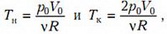
то изменение внутренней энергии равно
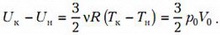
Полную работу найдем как площадь под кривой на рисунке 2:
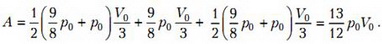
Тогда окончательно
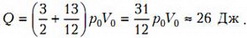
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
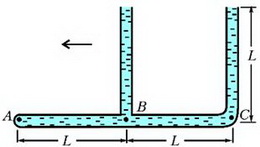
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
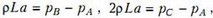
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
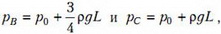
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
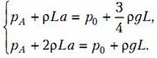
Решая эту систему относительно рА, найдем
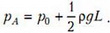
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
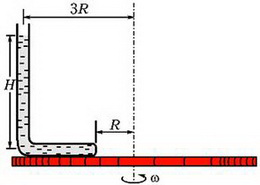
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
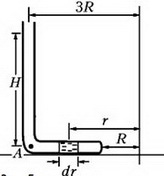
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
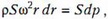
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
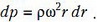
Проинтегрируем обе части этого уравнения и получим
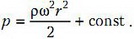
Константу определим из условия, что при r = 3R (точка А) давление равно
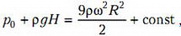
и получим зависимость p(r)
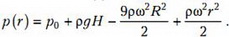
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
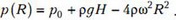
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
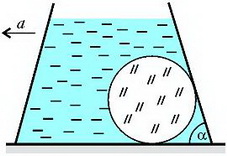
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
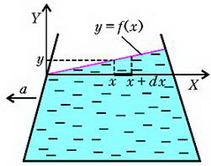
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
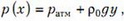
а с правого торца оно равно
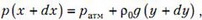
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
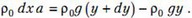
Отсюда получаем
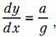
или в интегральном виде —
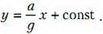
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
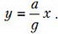
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
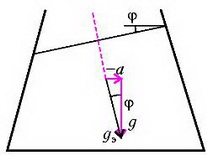
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
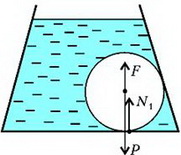
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
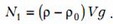
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
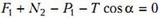
и по горизонтали:
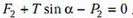
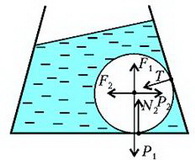
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
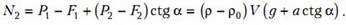
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.
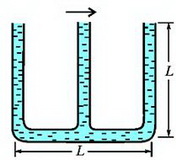
Рис. 11
4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.
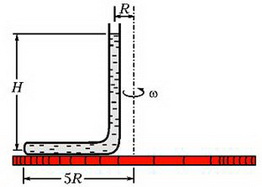
Рис. 12
Ответы.
1.
2.
3. .
4.
Источник



