В цилиндрическом сосуде с площадью основания 250 см2
Глава 13. Основы термодинамики
В большей части задач используется не общая форма первого закона термодинамики, а его различные частные формулировки, применимые к определённым процессам. Задачи на теплообмен в изолированной системе решаются с помощью уравнения теплового баланса (13.10).
При решении задач надо чётко выделять начальное и конечное состояния системы, а также характеризующие её параметры.
Задача 1. Во время расширения газа, вызванного его нагреванием, в цилиндре с площадью поперечного сечения S = 200 см2 газу было передано количество теплоты Q = 1,5 • 105 Дж, причём давление газа оставалось постоянным и равным р = 2 • 107 Па. На сколько изменилась внутренняя энергия газа, если поршень передвинулся на расстояние Δh = 30 см?
Р е ш е н и е. Согласно первому закону термодинамики в форме (13.12) Q = ΔU + А’, где А’ = pSΔh – работа, совершённая газом. Отсюда ΔU = Q – pSΔh = 30 кДж.

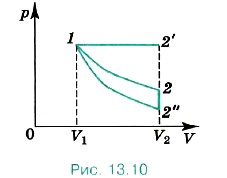
Задача 2. Газ расширяется от объёма V1 до объёма V2 один раз изотермически, другой изобарно и третий адиабатно. При каком процессе газ совершает большую работу и при каком газу передаётся большее количество теплоты?
Р е ш е н и е. На диаграмме р-V (рис. 13.10) изобразим все три процесса. Работа численно равна площади криволинейной трапеции. Из рисунка очевидно, что работа при изобарном процессе будет максимальной, при адиабатном минимальной, т. е. A’1 – 2′ > A’1-2 > A1-2″.
Температура газа в состоянии 2′ больше, чем в состоянии 2, а температура в состоянии 2 больше, чем в состоянии 2″ (Т2′ > Т2 > Т2″). В этом легко убедиться, начертив изотермы, проходящие через точки 2′ и 2″. При процессе 1-2′ изменение внутренней энергии AU > 0, при процессе 1-2 ΔU = 0. Очевидно, что поскольку Q = ΔU + А’ (первый закон термодинамики), то Q1-2′ > Q2 – 2 > Q1- 2″ (Q1 – 2″ = 0).
Задача 3. Пусть азот нагревается при постоянном давлении. Зная, что масса азота m = 280 г, количество затраченной теплоты Q = 600 Дж и удельная теплоёмкость азота при постоянном объёме cv = 745 Дж/(кг • К), определите, на сколько повысилась температура азота. Молярная масса азота М = 0,028 кг/моль.
Р е ш е н и е. Согласно первому закону термодинамики Q = ΔU + А’.
Изменение внутренней энергии ΔU = cvmΔT.
Работа при изобарном процессе А’ = pΔV = (m/M)RΔT.
Следовательно, Q = mΔT(cv + R/M), откуда
Задачи для самостоятельного решения
1. Для изобарного нагревания газа, взятого в количестве 800 моль, на 500 К газу сообщили количество теплоты 9,4 • 106 Дж. Определите работу газа и изменение его внутренней энергии.
2. В цилиндрическом сосуде с площадью основания 250 см2 находится азот массой 10 г, сжатый поршнем, на котором лежит гиря массой 12,5 кг. Какую работу совершит азот при нагревании его от 25 до 625 °С. На какую высоту при этом поднимется поршень? Атмосферное давление равно 1 атм.
3. Идеальный одноатомный газ в количестве 2 моль, находящийся при температуре 0 °С, сначала изохорно перевели в состояние, в котором давление в 2 раза больше первоначального, а затем изобарно в состояние, в котором объём в 2 раза больше первоначального. Определите изменение внутренней энергии газа.
4. В цилиндре под поршнем находится воздух. На его нагревание при постоянном давлении затрачено количество теплоты, равное 5 кДж. Определите работу, совершённую при этом воздухом. Теплоёмкость воздуха при постоянном давлении ср = 103 Дж/(кг • К), молярная масса 29 г/моль.
5. Положительна или отрицательна работа газа в процессах 1-2, 2-3 и 3-1 на рисунке 10.9? Получает газ тепло или отдаёт в этих процессах?
6. Какое количество теплоты необходимо для изохорного нагревания гелия массой 4 кг на 100 К?
7. Вычислите увеличение внутренней энергии водорода массой 2 кг при изобарном его нагревании на 10 К. (Удельная теплоёмкость водорода при постоянном давлении равна 14 кДж/(кг • К).)
8. В цилиндре компрессора сжимают идеальный одноатомный газ, количество вещества которого 4 моль. Определите, насколько поднялась температура газа за один ход поршня, если при этом была совершена работа 500 Дж. Процесс считайте адиабатным.
9. На одинаковые газовые горелки поставили два одинаковых плотно закупоренных сосуда вместимостью по 1 л. В одном сосуде находится вода, а в другом – воздух. Какой сосуд быстрее нагревается на 50 °С? Почему?
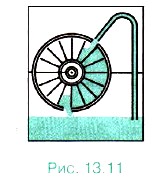
10. Предложен следующий проект вечного двигателя (рис. 13.11). Закрытый сосуд разделён на две половинки герметичной перегородкой, сквозь которую пропущены трубка и водяная турбина в кожухе с двумя отверстиями. Давление воздуха в нижней части больше, чем в верхней. Вода поднимается по трубке и наполняет открытую камеру. В нижней части очередная порция воды выливается из камеры турбины, подошедшей к отверстию кожуха. Почему данная машина не будет работать вечно?
11. В вакууме закреплён горизонтальный цилиндр, в котором слева находится гелий в количестве 0,1 моль, запертый поршнем. Поршень массой 90 г удерживается упорами и может скользить влево вдоль стенок цилиндра без трения. В поршень попадает пуля массой 10 г, летящая горизонтально со скоростью 400 м/с, и застревает в нём. Как изменится температура гелия в момент остановки поршня в крайнем левом положении? Считайте, что газ не успевает обменяться теплом с поршнем и цилиндром.
Источник
Задание 1. В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте
будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в см.
Решение. Заметим, что при переливании жидкости из одного сосуда в другой объём жидкости не изменился. Объём цилиндра равен произведению площади основания на высоту этого цилиндра. То есть V=Sh=pR2h. Поскольку в новом сосуде диаметр, а значит и радиус, в 2 раза больше, то площадь основания будет больше в 4 раза, значит высота, соответственно, уменьшится в 4 раза, то есть станет равна 48:4=12 см.
Ответ 12.
Задание 2. В цилиндрический сосуд, в котором находится 6 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
Решение. Заметим, что при опускании детали в сосуд изменение общего объёма равно объёму детали. Объём цилиндра равен произведению площади основания на высоту этого цилиндра. То есть V=Sh=pR2h. Так как уровень жидкости поднялся в 1,5 раза, значит объём увеличился тоже в 1,5 раза и стал равен 6*1,5 = 9. Объём детали равен 9 – 6=3.
Ответ 3.
Задания для самостоятельного решения. Все задания взяты из открытого банка заданий ФИПИ.
1. В цилиндрическом сосуде уровень жидкости достигает 98 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
2. В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
3. В цилиндрическом сосуде уровень жидкости достигает 256 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
4. В цилиндрическом сосуде уровень жидкости достигает 64 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
5. В цилиндрическом сосуде уровень жидкости достигает 96 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
6. В цилиндрическом сосуде уровень жидкости достигает 20 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
7. В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
8. В цилиндрическом сосуде уровень жидкости достигает 80 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
9. В цилиндрическом сосуде уровень жидкости достигает 405 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
10. В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз меньше диаметра первого? Ответ выразите в сантиметрах.
11. В цилиндрическом сосуде уровень жидкости достигает 45 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
12. В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
13. В цилиндрическом сосуде уровень жидкости достигает 294 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
14. В цилиндрическом сосуде уровень жидкости достигает 192 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
15. В цилиндрическом сосуде уровень жидкости достигает 147 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
16. В цилиндрическом сосуде уровень жидкости достигает 50 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
17. В цилиндрическом сосуде уровень жидкости достигает 320 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
18. В цилиндрическом сосуде уровень жидкости достигает 125 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
19. В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз меньше диаметра первого? Ответ выразите в сантиметрах.
20. В цилиндрическом сосуде уровень жидкости достигает 5 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза меньше диаметра первого? Ответ выразите в сантиметрах.
21. В цилиндрическом сосуде уровень жидкости достигает 6 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз меньше диаметра первого? Ответ выразите в сантиметрах.
22. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
23. В цилиндрическом сосуде уровень жидкости достигает 112 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
24. В цилиндрическом сосуде уровень жидкости достигает 32 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
25. В цилиндрическом сосуде уровень жидкости достигает 63 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
26. В цилиндрическом сосуде уровень жидкости достигает 384 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
27. В цилиндрическом сосуде уровень жидкости достигает 12 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
28. В цилиндрическом сосуде уровень жидкости достигает 28 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
29. В цилиндрическом сосуде уровень жидкости достигает 72 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз больше диаметра первого? Ответ выразите в сантиметрах.
30. В цилиндрическом сосуде уровень жидкости достигает 216 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз больше диаметра первого? Ответ выразите в сантиметрах.
31. В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза меньше диаметра первого? Ответ выразите в сантиметрах.
32. В цилиндрическом сосуде уровень жидкости достигает 567 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
33. В цилиндрическом сосуде уровень жидкости достигает 144 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз больше диаметра первого? Ответ выразите в сантиметрах.
34. В цилиндрическом сосуде уровень жидкости достигает 324 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
35. В цилиндрическом сосуде уровень жидкости достигает 243 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
36. В цилиндрический сосуд, в котором находится 10 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,6 раза. Чему равен объём детали? Ответ выразите в дм3.
37. В цилиндрический сосуд, в котором находится 4 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 2,5 раза. Чему равен объём детали? Ответ выразите в дм3.
38. В цилиндрический сосуд, в котором находится 8 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
39. В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Найдите объём детали. Ответ выразите в куб. см.
Источник
