В длинном вертикальном цилиндрическом сосуде
1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)
4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)
7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)
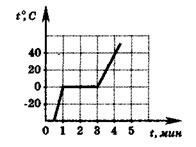8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)
9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)
10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)
11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)
12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)
13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)
14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.
(Решение)
15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)
16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)
19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)
(Решение)
20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)
21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)
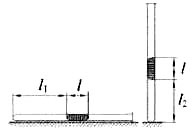22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)
23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)
24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)
25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)
26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)
27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)
Источник
Иродов – 2.113
Иродов 2.113. В каком случае к. п. д. цикла Карно повысится больше: при увеличении температуры нагревателя на ΔT или при уменьшении температуры холодильника на такую же величину? Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.110
Иродов 2.110. Горизонтально расположенную трубку с закрытыми торцами вращают с постоянной угловой скоростью ω вокруг вертикальной оси, проходящей через один из ее торцов. В трубке находится углекислый газ при температуре Т = 300 К. Длина трубки l = 100 см. Найти значение ω, при котором отношение концентраций молекул у противоположных, торцов трубки η = 2,0. […]
Смотреть материал
Иродов – 2.109
Иродов 2.109. Найти массу моля коллоидных частиц, если при вращении центрифуги с угловой скоростью ω вокруг вертикальной оси концентрация этих частиц на расстоянии r2 от оси вращения в η раз больше, чем на расстоянии r1 (в одной горизонтальной плоскости). Плотности частиц и растворителя равны соответственно ρ и ρ0. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.107
Иродов 2.107. Газ находится в очень высоком цилиндрическом сосуде при температуре Т. Считая поле тяжести однородным, найти среднее значение потенциальной энергии молекул газа. Как зависит эта величина от того, состоит ли газ из одного сорта молекул или из нескольких сортов? Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.106
Иродов 2.106. В очень высоком вертикальном цилиндрическом сосуде находится углекислый газ при некоторой температуре Т. Считая поле тяжести однородным, найти, как изменится давление газа на дно сосуда, если температуру газа увеличить в η раз. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.105
Иродов 2.105. В длинном вертикальном сосуде находится газ, состоящий из двух сортов молекул с массами m1 и m2, причем m2 > m1. Концентрации этих молекул у дна сосуда равны соответственно n1 и n2, причем n2 > n1. Считая, что по всей высоте поддерживается одна и та же температура Т и ускорение свободного падения равно g, […]
Смотреть материал
Иродов – 2.104
Иродов 2.104. Пусть η0 — отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а η — соответствующее отношение на высоте h = 3000 м. Найти отношение η/η0 при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.103
Иродов 2.103. При наблюдении в микроскоп взвешенных частиц гуммигута обнаружено, что среднее число их в слоях, расстояние между которыми h = 40 мкм, отличается друг от друга в η = 2,0 раза. Температура среды Т = 290 К. Диаметр частиц d = 0,40 мкм и их плотность на Δρ = 0,20 г/см3 больше плотности окружающей […]
Смотреть материал
Иродов – 2.100
Иродов 2.100. Идеальный газ, состоящий из молекул массы m с концентрацией n, имеет температуру Т. Найти с помощью распределения Максвелла число молекул, падающих в единицу времени на единицу поверхности стенки под углами ϑ, ϑ + dϑ к ее нормали. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.95
Иродов 2.95. Воспользовавшись распределением Максвелла, найти — среднее значение обратной скорости молекул идеального газа, находящегося при температуре Т, если масса каждой молекулы m. Сравнить полученную величину с обратной величиной средней скорости. Скачать решение: Скачать решение задачи
Смотреть материал
Источник
Абитуриенту
А. В.
Зотеев,
, МГУ им. М.В.Ломоносова, г. Москва;
А. А.
Склянкин,
МГУ им. М.В.Ломоносова, г. Москва
Окончание. См. № 02, 05,
09/09
Вариант 3 (окончание)
5. На длинную цилиндрическую проволочную катушку (соленоид) надет замкнутый проволочный виток. Если через соленоид пропускать переменный ток, в витке возникает индукционный ток. Во сколько раз k изменится сила индукционного тока, если диаметр проволоки, из которой сделан виток, увеличить в n = 2 раза?
Решение
Сопротивление проволочного витка
Здесь l – длина проволоки, а d – её диаметр. По закону Ома, сила тока ЭДС индукции i определяется скоростью изменения тока, протекающего через соленоид, и не зависит от параметров надетого витка. При увеличении диаметра d проволоки витка в 2 раза сила тока увеличится в k = 4 раза.
6. Небольшой брусок толкнули вверх по наклонной плоскости, сообщив начальную скорость υ0 = 2 м/с. Брусок поднялся на максимальную высоту h = 15 cм. Какова средняя скорость бруска при возвращении к основанию наклонной плоскости? Принять g = 10 м/с2.
Решение
Применим закон сохранения энергии. При движении бруска вверх а при движении вниз Здесь υ1 – конечное значение скорости при движении вниз. Важно отметить, что величина работы силы трения одинакова (и при этом, конечно, отрицательна) при движении как вверх, так и вниз. Исключив Атр, находим Как известно*, при равноускоренном движении без начальной скорости средняя скорость υср = υ1 /2. Поэтому
7. При температуре t = 0 °C почва покрыта слоем снега толщиной H = 10 см. Какой минимальной толщины h слой дождевой воды температуры t1 = 4 °C может полностью растопить снег? Удельная теплота плавления снега r = 3,4∙105 Дж/кг, его плотность ρ = 500 кг/м3; удельная теплоёмкость воды c = 4,2 ∙ 103 Дж /(кг ∙ К), а её плотность ρ0 = 103 кг/м3.
Решение
Плавление снега (или льда) может происходить за счёт теплоты, выделяющейся при охлаждении воды. Выделим мысленно на поверхности снега небольшую площадку площадью S. Запишем уравнение теплового баланса для процесса таяния снега и охлаждения воды, находящихся в мысленно выделенном цилиндре с основанием S: rρSH = cρ0ShΔt. Отсюда найдём
Здесь Δt = 4 °C.
8. В вертикальном цилиндрическом сосуде радиусом R = 10 см находится жидкость. В ней плавает шар радиусом r = 5 см. Плотность материала шара в k = 2 раза меньше плотности жидкости. На сколько сантиметров понизится уровень жидкости в сосуде, если шар из неё удалить?
Решение
По закону Архимеда и с учётом соотношения плотностей, плавающий шар погружён в жидкость наполовину. Объём погруженной части шара равен
V = (2/3)πr3.
После удаления шара из жидкости объём ранее вытесненной шаром жидкости «распределится равномерно» по сечению сосуда. Её уровень понизится на
9. Поверхность солнечной батареи, площадь которой S = 1 м2, расположена так, что солнечные лучи падают на неё по нормали. Найти коэффициент полезного действия батареи h, если известно, что батарея обладает (выдаёт на выходе) электрической мощностью W = 20 Вт, а плотность потока энергии солнечных лучей, падающих на батарею, равна I = 1,4 · 103 Дж · с-1 · м-2 .
Решение
По определению интенсивности, мощность излучения, падающего на батарею, Wзатр = IS. Коэффициент полезного действия
10. Небольшой груз подвешен на пружинке жёсткостью k = 40 Н/м перед собирающей линзой оптической силой D = 5 дптр. Расстояние от линзы до груза d = 30 см. Груз совершает вертикальные колебания. Энергия этих колебаний равна W = 2 ∙ 10–3 Дж. Найдите амплитуду колебаний А изображения груза, даваемого линзой.
Решение
При гармонических колебаниях полная энергия колебаний равна Отсюда амплитуда колебаний груза Расстояние от линзы до изображения груза находится из формулы линзы
Амплитуду колебаний изображения можно найти с учётом увеличения, даваемого линзой:
Вариант 4
1. Сформулируйте законы преломления света.
2. Дайте определение понятия «напряжённость электрического поля».
3. Выведите формулу для эквивалентной ёмкости последовательно соединённых конденсаторов С1 и С2.
Решение
При последовательном соединении конденсаторов общее напряжение между крайними обкладками U = U1 + U2, где U1 и U2 – напряжения на обкладках каждого конденсатора. При этом абсолютные величины зарядов на каждой из обкладок одинаковы: |q1| = |q2| = q.
Из определения электроёмкости U1 = q1/С1 и U2 = q2/С2. С учётом написанных соотношений получаем .
Отсюда
4. Материальная точка движется вдоль оси ОХ. На рисунке приведена зависимость её координаты x от времени t. Найдите максимальное значение модуля скорости движения точки υ.
Решение
Модуль скорости пропорционален тангенсу угла наклона графика зависимости координаты от времени. Значение скорости максимально в интервале от t1 = 2 c до t2 = 3 c. По определению скорости, её модуль
Значения Δx = –10 м и Δt = 1 с определяются по графику. Таким образом, υmax = 10 м/с.
5. Предмет помещён перед рассеивающей линзой на двойном фокусном расстоянии. Во сколько раз k линейный размер предмета отличается от размера его изображения?
Решение
Применяем формулу линзы Знак «минус» в левой части говорит о том, что линза – рассеивающая, а в правой – о том, что изображение мнимое и находится перед линзой, как и сам предмет. Учтём, что d = 2F, и найдём отсюда Увеличение, даваемое линзой: Г = f/d = 1/3. То есть предмет больше изображения в k = 1/Г = d/f = 3 раза.
6. Теннисный мячик перелетает горизонтально точно над сеткой и ударяется в корт. Какова высота отскока мячика h, если при ударе о корт теряется h = 0,4 кинетической энергии мячика, связанной с его вертикальным движением? Высота сетки Н = 1 м.
Решение
Согласно условию, потеря энергии ηmgH. Оставшаяся энергия mgH – ηmgH перейдёт в потенциальную энергию подъёма мяча после удара о корт: (1 – η)mgH = mgH. Отсюда h = (1 – η)H = 0,6 м.
7. Неоднородное бревно AB длиной L = 5 м лежит на земле. К концу бревна А прикладывают вертикальную силу. При величине этой силы F1 = 480 Н (или больше) этот конец бревна отрывается от земли. Чтобы оторвать от земли другой конец бревна В, к нему надо приложить силу не меньше, чем F2 = 320 H. На каком расстоянии от конца А находится центр тяжести бревна?
Решение
Рассмотрим неподвижное бревно в горизонтальном положении, когда на него одновременно действуют силы F1, F2 и сила тяжести. Применим правило моментов, вычисляя моменты сил относительно оси, перпендикулярной бревну и проходящей, например, через центр тяжести бревна. Согласно правилу моментов, F1 · x = F2(L – x). Отсюда
* Убедиться в этом несложно, записав соответствующие выражения для перемещения и скорости.
Источник