В длинном вертикальном сосуде находится однородный газ
2.1. В сосуде объемом 1 л находится кислород массой 1 г. Определить концентрацию молекул.
| =10-3 м3m=1 г = 10-3 кгМ=32×10-3кг/моль |
| n – ? |
Решение. p=nkT, Þ . , Þ , подставляем в правую часть выражения в рамке: . Ответ: n=1,88×1025м-3.
2.2 Найти среднюю скорость молекул идеального газа, плотность которого при давлении 35 кПа равна 0,3 кг/ м-3.
| р=35×103Паr=0,3 кг/ м-3 |
| <u>– ? |
Решение. Запишем основное уравнение молекулярно-кинетической теории идеального газа в виде , где mo – масса отдельной молекулы. Средняя скорость равна , а среднеквадратичная , Þ . , Þ , Þ . Подставим в выражение в рамке:
. Ответ: м/с.
2.3. На какой высоте давление составляет 60 % от давления на уровне моря? Считать температуру равной 10 оС, независимо от высоты.
| t=10 оСp=0,6po M=29×10-3кг/моль |
| h– ? |
Решение. Из барометрической формулы следует, что отношение давлений на высоте h и на уровне моря равно , Þ . Обратите внимание: чтобы избавиться от минуса, мы перевернули дробь. Осталось выразить h из последней формулы: . Ответ: h=4220 м.
2.4. Считая температуру равной 273 К и не зависящей от высоты, определить, на какой высоте над уровнем моря плотность воздуха уменьшится в е раз.
| t=273 Кr=0,6ro M=29×10-3кг/моль |
| h– ? |
Решение. Из уравнения Клапейрона-Менделеева выразим давление через протность: = , и подставим в барометрическую формулу: , Þ , Þ , Þ 1= . Отсюда выразим искомую высоту: =8000 м. Ответ: h=8 км.
2.5. В длинном вертикальном сосуде находится смесь из двух газов, у которых массы молекул соответственно равны m1 и m2. Концентрации молекул газов у дна сосуда равны соответственно n01 и n02. Найти высоту, на которой концентрации газов будут одинаковы. Считать температуру одинаковой по всей высоте.
Решение. Запишем барометрическую формулу для каждой компоненты смеси: ; . При n1=n2 после несложных преобразований имеем . Логарифмируем последнее выражение, а затем выразим искомую высоту: . Ответ: .
2.6. Четыре моля кислорода находятся при температуре 27 оС. Найти его внутреннюю энергию.
| t=27 оС = 300 Кn=4 i=5 |
| U– ? |
Решение. Внутренняя энергия идеального газа не зависит от вида газа, а определяется только количеством молей и абсолютной температурой:
, где для двухатомной жесткой молекулы кислорода число степеней свободы i=5. Отсюда = 25×103Дж. Ответ: U = 25×103Дж.
2.7. Определить плотность смеси водорода массой m1 =8 г и кислорода массой m2 = 64 г при температуре Т=290 К и давлении 0,1 МПа.
| Т = 290 Кр= 0,1 МПа m1 =8 г=8×10-3 кгm2 = 64×10-3 кгМ1=2×10-3кг/моль М2=32×10-3кг/моль |
| r – ? |
Решение. r= (1), m= m1+ m2 (2), (3), Þ (4). Подставляя (2) и (4) в (1), получим искомое выражение для плотности смеси газов: (кг/м3).
Ответ: r = 0,498 кг/м3.
2.8. Один моль некоторого идеального газа изобарически нагрели на DТ = 72 К, сообщив ему количество теплоты Q=1,6 кДж. Найти приращение его внутренней энергии и показатель адиабаты .
| DТ = 72 К n=1 Q=1,6 кДж |
| DU– ? γ– ? |
Решение. Количество теплоты, необходимое для нагревания 1 моля газа, равно
, откуда , откуда, раскрывая скобки, выражаем γ:
. Приращение внутренней энергии равно = , где мы подставили ранее найденное γ: .
Ответ: DU=1 кДж, γ=1.6
2.9. Идеальный газ с показателем адиабаты γ расширяют так, что сообщаемое ему тепло равно убыли его внутренней энергии. Найти молярную теплоемкость газа в этом процессе и уравнение процесса в параметрах TV.
Решение. По условию , поэтому молярная теплоемкость равна , . Это процесс с постоянной теплоемкостью, т.е. политропический. Показатель политропы , где мы подставили найденную выше теплоемкость С. В уравнение политропы в форме =const, подставим n:
. Ответ: ; .
2.10. Во сколько раз надо расширить адиабатически газ, состоящий из жестких двухатомных молекул, чтобы их средняя квадратичная скорость уменьшилась в η=1,5 раза?
Решение. Обозначим искомое отношение объемов: . По условию , где слева отношение начальной и конечной среднеквадратичных скоростей, каждая из которых пропорциональна корню квадратному из температуры. Следовательно, . При адиабатическом процессе =const, Þ = , Þ = , Þ . Осталось подставить показатель адиабаты: , Þ β= .
Ответ: .
2.11. Водород совершает цикл Карно. Найти кпд цикла, если при адиабатическом расширении объем газа увеличивается в n=2 раза.
Решение. При адиабатическом процессе =const, Þ = , Þ , Þ кпд цикла равен η= = . Ответ: 0,25.
2.12. Водород совершает цикл Карно. Найти кпд цикла, если при адиабатическом расширении давление газа уменьшается в n=2 раза.
Решение. Уравнение адиабаты =const, Þ = , Þ . По условию , Þ . Из уравнения Клапейрона-Менделеева ( ) следует, что ; , Þ , что подставляем в формулу для кпд: η= = . Ответ: =0,18.
2.13. Найти приращение энтропии 1 моля углекислого газа при увеличении его температуры в n=2 раза при изобарическом процессе.
| n=2 p=const n=1 γ= 7/5 |
| – ? |
Решение. Энтропия 1 моля идеального газа равна . Следовательно, изменение энтропии при переходе из состояния 1 в состояние 2 равно , где . Жесткая молекула углекислого газа линейна и поэтому имеет 5 степеней свободы, Þ γ= 7/5. Окончательно получаем (Дж/К). Ответ: Дж/К.
2.14. Один моль кислорода изохорически нагревается от температуры T1 до температуры T2=4T1. Найти приращение энтропии.
| n=4 V=const n=1 γ= 7/5 |
| – ? |
Решение. Запишем энтропию 1 моля идеального газа в фирме . Тогда изменение энтропии при переходе из состояния 1 в состояние 2 равно = . Поскольку молекула кислорода линейная, то если считать ее жесткой, то γ= 7/5, т.к. число степеней свободы =5. Отсюда Ответ: Дж/К.
2.15. Азот массой 28 г адиабатно расширили в n=2 раза, а затем изобарно сжали до исходного объема. Определить изменение энтропии в ходе указанных процессов.
Решение. Обозначим адиабатный переход 1®2, а изобарный 2®3. Полное изменение энтропии равно сумме: = + . Изменение энтропии на участке 1®2: =0, так как адиабатный процесс идет без теплообмена, Þ , Þ =0. Изменение энтропии на участке 2®3 равно = . При р=const ; . Подставляя в формулу = , получим: = = . Ответ: Дж/К.
2.16. Считая процесс образования мыльного пузыря изотермическим, определить работу А, которую надо совершить, чтобы увеличить его диаметр от d1=6 мм до d2=60 мм. Поверхностное натяжение мыльного раствора принять равным s=40 мН/м.
| d1=6×10-3 мd2=60×10-3 мТ=const s=40×10-3Н/м |
| А – ? |
Решение. Величину поверхностного натяжения можно выразить двумя способами: либо как силу натяжения, приходящуюся на единицу длины контура, либо как поверхностную энергию, приходящуюся на единицу площади поверхности: . В последнем случае, искомую работу следует приравнять изменению энергии в результате раздувания пузыря, а -полагать изменением площади поверхности с учетом того, что у пузыря две поверхности: внешняя и внутренняя. Таким образом, , где . При Т=const,Þ s=const. Таким образом, = . Ответ: А=896×10-6Дж.
2.17. Капилляр, имеющий внутренний радиус r=0,5 мм, опущен в жидкость. Определить массу жидкости, поднявшейся в капилляре, если ее поверхностное натяжение равно 60 мН/м.
| r=0,5 ×10-3 мs=60×10-3Н/м |
| m – ? |
Решение. Сила тяжести столба жидкости в капилляре уравновешена силами поверхностного натяжения в связи со смачиванием внутренних стенок капилляра жидкостью: , где l=2pr – длина границы. Отсюда .
Ответ: m=1,92×10-5 кг.
Источник
Иродов – 2.113
Иродов 2.113. В каком случае к. п. д. цикла Карно повысится больше: при увеличении температуры нагревателя на ΔT или при уменьшении температуры холодильника на такую же величину? Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.110
Иродов 2.110. Горизонтально расположенную трубку с закрытыми торцами вращают с постоянной угловой скоростью ω вокруг вертикальной оси, проходящей через один из ее торцов. В трубке находится углекислый газ при температуре Т = 300 К. Длина трубки l = 100 см. Найти значение ω, при котором отношение концентраций молекул у противоположных, торцов трубки η = 2,0. […]
Смотреть материал
Иродов – 2.109
Иродов 2.109. Найти массу моля коллоидных частиц, если при вращении центрифуги с угловой скоростью ω вокруг вертикальной оси концентрация этих частиц на расстоянии r2 от оси вращения в η раз больше, чем на расстоянии r1 (в одной горизонтальной плоскости). Плотности частиц и растворителя равны соответственно ρ и ρ0. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.107
Иродов 2.107. Газ находится в очень высоком цилиндрическом сосуде при температуре Т. Считая поле тяжести однородным, найти среднее значение потенциальной энергии молекул газа. Как зависит эта величина от того, состоит ли газ из одного сорта молекул или из нескольких сортов? Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.106
Иродов 2.106. В очень высоком вертикальном цилиндрическом сосуде находится углекислый газ при некоторой температуре Т. Считая поле тяжести однородным, найти, как изменится давление газа на дно сосуда, если температуру газа увеличить в η раз. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.105
Иродов 2.105. В длинном вертикальном сосуде находится газ, состоящий из двух сортов молекул с массами m1 и m2, причем m2 > m1. Концентрации этих молекул у дна сосуда равны соответственно n1 и n2, причем n2 > n1. Считая, что по всей высоте поддерживается одна и та же температура Т и ускорение свободного падения равно g, […]
Смотреть материал
Иродов – 2.104
Иродов 2.104. Пусть η0 — отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а η — соответствующее отношение на высоте h = 3000 м. Найти отношение η/η0 при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.103
Иродов 2.103. При наблюдении в микроскоп взвешенных частиц гуммигута обнаружено, что среднее число их в слоях, расстояние между которыми h = 40 мкм, отличается друг от друга в η = 2,0 раза. Температура среды Т = 290 К. Диаметр частиц d = 0,40 мкм и их плотность на Δρ = 0,20 г/см3 больше плотности окружающей […]
Смотреть материал
Иродов – 2.100
Иродов 2.100. Идеальный газ, состоящий из молекул массы m с концентрацией n, имеет температуру Т. Найти с помощью распределения Максвелла число молекул, падающих в единицу времени на единицу поверхности стенки под углами ϑ, ϑ + dϑ к ее нормали. Скачать решение: Скачать решение задачи
Смотреть материал
Иродов – 2.95
Иродов 2.95. Воспользовавшись распределением Максвелла, найти — среднее значение обратной скорости молекул идеального газа, находящегося при температуре Т, если масса каждой молекулы m. Сравнить полученную величину с обратной величиной средней скорости. Скачать решение: Скачать решение задачи
Смотреть материал
Источник
Окончательно с.
Задача 2. Метеорологическая ракета. Метеорологическая ракета стартует в вертикальном направлении с поверхности Земли. Ее топливо сгорает за τ = 40 с полета. В течение этого времени ускорение ракеты возрастает линейно от а0 = g до аτ = 5g. Найдите мощность двигателя ракеты перед окончанием его работы. Масса не заправленной ракеты m0 = 10 кг, ускорение свободного падения g = 10 м/с2.
Возможное решение
Ускорение ракеты а(t) = а0 + (аτ – а0).
По аналогии с тем, что пройденному пути соответствует площадь под графиком скорости, находим скорость Vτ ракеты в момент τ как площадь под графиком ускорения (рис.13): Vτ= τ ( аτ + а0)/2.
Согласно второму закону Ньютона, m аτ =F–mg, где F — сила тяги в конце полета. Мощность двигателя в этот момент
N = F Vτ = ( аτ + g) ( аτ + а0) = 720 кВт.
Задача 3. Тяжелый поршень. В теплоизолированном цилиндрическом сосуде с вертикальными гладкими стенками на небольших опорах лежит тяжелый однородный поршень толщиной h и плотностью ρ (рис. 14). Под поршнем находится газ массой m c удельной теплоемкостью C. Первоначально давление газа внутри цилиндра равно атмосферному. Газ начинают нагревать, при этом увеличение его давления Δp = α mΔt, где α – заданная константа, Δt – изменение температуры. Какое минимальное количество Q подвести к газу, чтобы поршень сдвинулся с места?
Возможное решение
Пусть М — масса поршня, S — площадь его основания, тогда чтобы он сдвинулся с места, давление газа в цилиндре должно превысить атмосферное на величину
.
Из связи Δр и Δt находим . Следовательно, Q=cmΔt = .
Задача 4. Сосуд на опорах Легкий цилиндрический сосуд с жидкостью плотностью ρ0 стоит на двух параллельных опорах, силы реакций которых составляют N1 и N2 (рис. 15). В сосуд опустили на нити шарик массой m и плотностью ρ так, что он оказался на одной вертикали со второй опорой. При этом шарик полностью погружен в воду и не касается сосуда. Определите новые силы N‘1 и N‘2 реакций опор.
Возможное решение
Пусть F и F’ — силы давления жидкости на основание сосуда до и после погружения шарика, тогда F’ =F +.
Поскольку сосуд легкий и цилиндрический, то при увеличении уровня воды центр масс сосуда с водой не смещается по горизонтали. Следовательно, точки приложения сил F и F‘ совпадают. Запишем условия равновесия сосуда до и после погружения шарика:
N1+N2= F, N‘1+N‘2= F‘, N1l1 = N2l2, N‘1l1 = N‘2l2, где l1 и l2 — плечи реакций опор относительно точки приложения силы F.
Откуда N‘1 = N1, N‘2 = N2.
Заметим, что ответ не зависит от места погружения шарика.
Задача 5. Измерения в электрической цепи. Семь резисторов сопротивлениями R1=1кОм, R2=2кОм, R3=0,5кОм, R4=2,5кОм, R5=2кОм, R6=1кОм, R7=1кОм соединены с источником постоянного напряжения U=30 В (рис.16). К резисторам подключили два вольтметра и два амперметра. Определите их показания V1, V2, I1, I2. Приборы считайте идеальными.
Возможное решение
Перерисуем схему без вольтметров (рис. 17). Сопротивление каждой из параллельных ветвей цепи составляет r = R1 + R2 = R3 + R4= R5 + R6 = 3 кОм, поэтому полное сопротивление цепи
кОм.
Через резистор R7 сила тока I = U/R. Через каждую из параллельных ветвей цепи течет одинаковый ток, поэтому сила тока в каждой из них i = I/3, откуда
I1= I2=2i=2U/3R=10 мА.
Показания V1 и V2 вольтметров найдем как напряжения между соответствующими точками: В, В.
10 класс
Задача 1. Клин и шайба (1). Вблизи вершины клина массой М, высотой Н и с длиной основания L удерживают небольшую шайбу массой m (рис. 18). Клин покоится на гладкой горизонтальной поверхности. Шайбу отпускают и она соскальзывает к основанию клина. На какое расстояние S при этом переместится клин?
Возможное решение
Поскольку внешние силы, действующие на систему «клин-шайба», не имеют горизонтальных составляющих, горизонтальная координата центра масс системы не меняется: m(L – S) – MS = 0, откуда S = .
Задача 2. Клин и шайба (2). При выполнении условий предыдущей задачи найдите максимальную скорость V клина. Трением между клином и шайбой пренебречь.
Возможное решение
Скорость клина будет максимальной, когда шайба достигнет его основания. Пусть – скорость шайбы в этот момент относительно клина, а – ее скорость в неподвижной системе отсчета (рис. 22). По теореме косинусов для треугольника скоростей:
v2 = u2 + V2 – 2uVcos a. (1)
Поскольку внешние силы, действующие на систему «клин-шайба» вертикальны, проекция импульса системы на ось х не меняется: О = m(u cos a – V) – MV, откуда
(2).
По закону сохранения энергии: mgH =
Подставив (1) и (2) в последнее уравнение и учитывая, что cos а = , найдем .
Задача 3. Стакан-поплавок. В глубоком цилиндрическом сосуде с внутренним диаметром D находится вода, в которой дном вниз плавает тонкостенный металлический стакан массой m и высотой H. Благодаря направляющим стенки стакана и цилиндра остаются параллельными. Какую минимальную работу А нужно совершить, чтобы утопить этот стакан, то есть заставить его пойти ко дну? Известно, что утопленный стакан не всплывает, а максимальная масса вмещаемой им воды равна М.
Возможное решение
Будем медленно опускать стакан в воду. Для этого к нему нужно прикладывать вертикально вниз силу F, уравновешивающую сумму силы Архимеда и силы тяжести, действующие на стакан. Пока в стакане нет воды, F линейно зависит от глубины погружения х, причем F(0) = 0.
Край стакана сравняется с уровнем жидкости в сосуде при х = х1, (рис. 20). При этом
F(x1) = Мg – mg = F.
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Источник
При ознакомлении с демонстрационным вариантом контрольных измерительных материалов 2017 г. следует иметь в виду, что задания, включённые в демонстрационный вариант, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ в 2017 г. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2017 г., приведён в кодификаторе элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена 2017 г. по физике.
Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику ЕГЭ и широкой общественности составить представление о структуре будущих КИМ, количестве и форме заданий, об уровне их сложности. Приведённые критерии оценки выполнения заданий с развёрнутым ответом, включённые в этот вариант, дают представление о требованиях к полноте и правильности записи развёрнутого ответа.
Эти сведения позволят выпускникам выработать стратегию подготовки и сдачи ЕГЭ.
Инструкция по заполнению бланков ЕГЭ.
*) В конце теста вы найдете полное решение всех задач варианта.
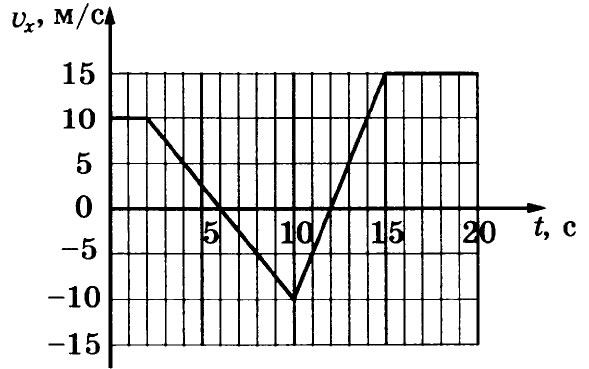
1. На рисунке приведён график зависимости проекции скорости тела их от времени. Чему
равна проекция ускорения этого тела ах в интервале времени от 10 до 15 с?
Ответ:
м/с2
2. У поверхности Земли на космонавта действует гравитационная сила 900 Н. Какая гравитационная сила действует со стороны Земли на того же космонавта в космическом корабле, который движется по круговой орбите на расстоянии двух радиусов Земли от земной поверхности?
Ответ:
Н
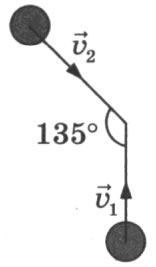
3. Одинаковые шары,массой 0,4 кг каждый движутся со скоростями, показан
ными на рисунке, и при столкновении слипаются. Чему будет равен суммарный импульс шаров после столкновения, если v1 = 4 м/с, v2 =v1√2?
Ответ:
кг·м/с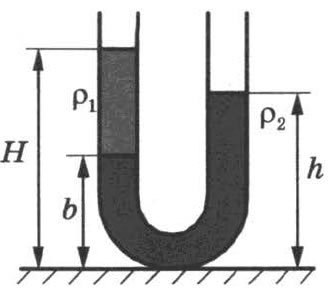
4. В широкую U-образную трубку, расположенную вертикально, налиты жидкости плотно
стью ρ1 и ρ2 (см. рисунок). Жидкости не смешиваются. На рисунке b = 15 см, h = 30 см,
Н = 35 см. Чему равно отношение плотностей ρ1/ρ2?
Ответ:
5. Четыре тела одинаковой массы 100 г двигались вдоль оси Ох. В таблице представлена
зависимость их координат от времени.
| t, с | 1 | 2 | 3 | 4 | 5 | |
| X1, см | 4 | 8 | 18 | 32 | 50 | |
| x2, см | 2 | 2 | 2 | 2 | 2 | 2 |
| X3, см | 2 | 4 | 6 | 8 | 10 | |
| x4, см | 2 | -2 | 2 |
Выберите из предложенных утверждений двау которые верно отражают результаты этого
опыта.
1) Первое тело двигалось равномерно.
2) Сумма сил, дейтсвующих на второе тело, равна нулю.
3) Скорость третьего тела равна 2 м/с.
4) Период колебаний четвертого тела равен 2 с.
5) В момент времени 3 с кинетическая энергия третьего тела была равна 0,4 Дж.
Ответы №№:
6. Шарик, брошенный от поверхности земли вертикально вверх с начальной скоростью v0,
поднялся на высоту Н, а затем упал обратно на землю. Что произойдет с ускорением шарика и его максимальной потенциальной энергией относительно земной поверхности, если
уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь.
Для каждой величины определите соответствующий характер ее изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Ускорение шарика. Максимальная потенциальная энергия относительно земной поверхности:
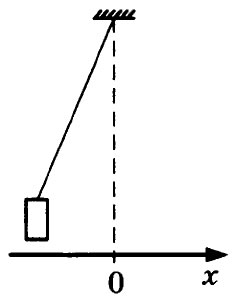7. Груз, привязанный к нити, отклонили от положения равновесия и отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин,
характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут
представлять.
К каждой позиции первого столбца подберите соответствующую позицию из второго
столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
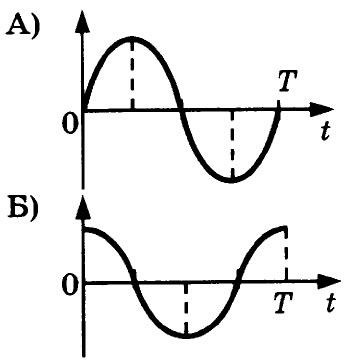 | 1) кинетическая энергия Ек 2) координата х 3) проекция импульса рх, 4) проекция ускорения ах |
Ответы АБ:
8. Объём 1 моль водорода в сосуде при температуре Т и давлении р равен 3 л. Чему равен
объём 3 моль водорода при том же давлении и температуре 2Т? (Водород считать идеальным газом.)
Ответ:
л
9. Кусок металла с удельной теплоёмкостью 450 Дж/(кг·К) нагрели от 20 °С до 60 °С,
затратив количество теплоты, равное 36 кДж. Чему равна масса этого куска металла?
Ответ:
кг
10. Газ в цилиндре расширился, совершив работу 150 Дж. Внутренняя энергия газа при этом
уменьшилась на 30 Дж. Какое количество теплоты газ получил от окружающих тел?
Ответ:
Дж
11. В жёстком закрытом сосуде находится влажный воздух при температуре 16 °С. Плотность водяных паров в сосуде равна 1,155·10-2 кг/м3. Воздух в сосуде нагревают до
25 °С. Пользуясь таблицей зависимости плотности насыщенных паров воды от температуры, выберите два верных утверждения о результатах этого опыта.
| t, °С | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| pнп, 10-2 кг/м3 | 1,36 | 1,45 | 1,54 | 1,63 | 1,73 | 1,83 | 1,94 | 2,06 | 2,18 | 2,30 |
1) При температуре 16 °С на стенках сосуда есть капельки росы.
2) Относительная влажность воздуха в сосуде при 18 °С равна 75%.
3) При увеличении температуры относительная влажность воздуха в сосуде уменьшается.
4) Давление в сосуде остаётся постоянным.
5) Плотность водяного пара в сосуде при нагревании увеличивается.
Ответы №№:
12. В ходе адиабатного процесса внутренняя энергия 1 моль разреженного гелия увеличивается. Как изменяются при этом температура гелия и его давление?
Для каждой величины определите соответствующий характер
изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
Температура гелия/ Давление гелия: 
13. Электрон е влетает в зазор между полюсами электромагнита со скоростью v→направленной к наблюдателю перпендикулярно плоскости рисунка (см. рисунок, где кружок с
точкой показывает направление движения электрона). Как направлена (вправо, влево,
вверх, вниз, к наблюдателю, от наблюдателя) действующая на него сила Лоренца F?→
Ответ запишите словом (словами).
Ответ:
14. Заряженная пылинка массой m с зарядом q движется с ускорением а = 20 м/с2 в однородном электрическом поле напряжённостью Е. Каково ускорение пылинки массой 2m
с зарядом 3q в том же поле? (Силой тяжести, действующей на пылинку, пренебречь.)
Ответ:
м/с2
15. Индуктивность одного витка проволоки равна 4·10-3 Гн. При какой силе тока магнитный поток через поперечное сечение катушки, сделанной из 5 витков, равен 20 мВб?
Ответ:
A
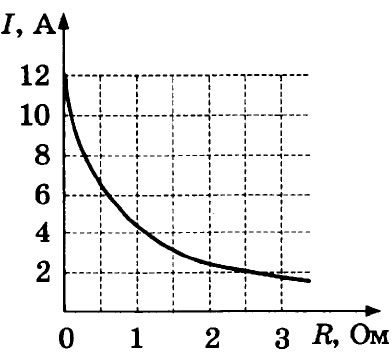
16. К аккумулятору подключили реостат. На рисунке показан график изменения силы тока
в реостате в зависимости от его сопротивления. Выберите из предложенных утверждений два у которые верно отражают результаты этого опыта.
1) Внутреннее сопротивление аккумулятора равно 0,5 Ом.
2) ЭДС аккумулятора равна 12 В.
3) Мощность, выделяемая в реостате увеличивается при увеличении его сопротивления.
4) Напряжение на реостате при силе тока 2 А равно 5 В.
Напряжение на источнике не зависит от силы тока через реостат.
Ответы №№: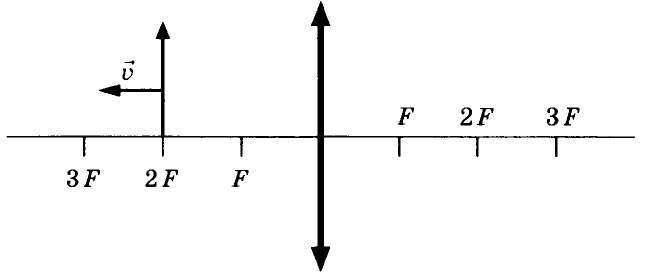 
17. Предмет, расположенный на двойном фокусном расстоянии от тонкой собирающей линзы, передвигают к тройному фокусу (см. рисунок). Как изменятся при этом расстояние
от линзы до изображения предмета и размер
изображения?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Расстояние от линзы до изображения. Размер изображения:
18. Участок цепи постоянного тока содержит резистор. Установите соответствие между формулами для вычисления физических величин и названиями этих величин.
В формулах использованы обозначения: I — сила тока на участке цепи; U — напряжение на участке цепи, t — время протекания тока.
К каждой позиции первого столбца подберите соответствующую позицию из второго
столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФОРМУЛЫ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| А) IU Б) It | 1) заряд, протекший через резистор 2) напряжение на резисторе 3) мощность тока, выделяющаяся на резисторе 4) сила тока через резистор |
Ответы АБ:
19. Ядро магния 2412Mg захватило электрон. Определите число протонов и нейтронов в этом
ядре, образовавшемся в результате такой реакции.
Число протонов. Число нейтронов:
20. На рисунке представлен фрагмент спектра излучения атомарных паров водорода. Цифры
на числовой оси — длины волн в нанометрах. Чему равна минимальная энергия фотонов
на данном участке спектра? Ответ округлить до целого значения.
Ответ:
·10-19Дж
21. В ядерном реакторе цепочка ядерных реакций начинается с захвата ядром быстрого
нейтрона. Как изменятся при захвате нейтрона следующие характеристики ядра: заряд
ядра и число нуклонов в ядре?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется.
Запишите выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
Заряд ядра. Число нуклонов в ядре:
22. С помощью амперметра проводились измерения силы тока на участке цепи. Шкала амперметра проградуирована в А. Погрешность измерений силы тока равна половине цены
деления шкалы амперметра. Запишите в ответ величину силы тока в цепи с учётом погрешности измерений.
Ответ: ( ±
) А
23.Необходимо собрать экспериментальную устаповку, с помощью которой можно определить ускорение тела, соскальзывающего с наклонной плоскости. Для этого школьник
взял брусок и наклонную плоскость. Какие два предмета из приведённого ниже перечня
оборудования необходимо дополнительно использовать для проведения этого эксперимента?
1) динамометр
2) пружина
3) секундомер
4) линейка
5) весы
Ответы №№:
24. Рассмотрите таблицу, содержащую некоторые характеристики планет Солнечной системы. Размеры и параметры орбит даны в сравнении с планетой Земля.
Выберите два утверждения, которые соответствуют характеристикам планет.
1) Средняя плотность Венеры меньше средней плотности Земли.
2) Центростремительное ускорение Юпитера при его вращении вокруг Солнца больше
центростремительного ускорения Марса.
3) Первая космическая скорость для Нептуна меньше, чем для Урана.
4) Ускорение свободного падения на Меркурии составляет примерно1 м/с2.
5) Сила притяжения Сатурна к Солнцу больше, чем у Юпитера.
| Имя | Диаметр | Масса | Орбитальный радиус (а.е.) | Период обращения (земных лет) | Период вращения (земных суток) | |
| Меркурий | 0,38 | 0,06 | 0,39 | 0,24 | 58,6 | |
| Венера | 0,95 | 0,82 | 0,72 | 0,62 | 243 | |
| Земля | 1 | 1 | 1 | 1 | 1 | |
| Марс | 0,53 | 0,11 | 1.5 | 1,9 | 1 | |
| Юпитер | 11,2 | 318 | 5.2 | 11,9 | 0,41 | |
| Сатурн | 9,5 | 95,2 | 9.5 | 29,5 | 0,43 | |
| Уран | 4 | 14,6 | 19.2 | 84 | 0,72 | |
| Нептун | 3,9 | 17,2 | 30,1 | 165 | 0,67 | |
Ответы №№: Часть II.
25. Снаряд, летящий со скоростью 100 м/с, разрывается на два осколка. Один из осколков
летит под углом 90° к первоначальному направлению, а второй — под углом 60°. Какова
масса снаряда до разрыва, если второй осколок массой 1 кг имеет скорость 400 м/с?
Массой взрывчатого вещества пренебречь.
Ответ:
кг
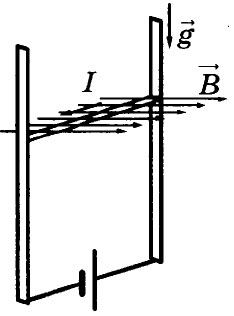
26. В однородном магнитном поле по вертикальным направляющим без
трения скользит прямой горизонтальный проводник массой 0,2 кг, по
которому течёт ток 2 А. Вектор магнитной индукции направлен горизонтально перпендикулярно проводнику (см. рисунок), В = 2 Тл. Чему
равна длина проводника, если известно, что ускорение проводника направлено вниз и равно 2 м/с2?
Ответ:
м
27. Предмет расположен на горизонтальной главной оптической оси тонкой собирающей
линзы. Оптическая сила линзы D = 5 дптр. Изображение предмета действительное, увеличение (отношение высоты изображения предмета к высоте самого предмета) k = 2.
Найдите расстояние от изображения предмета до линзы.
Ответ:
см
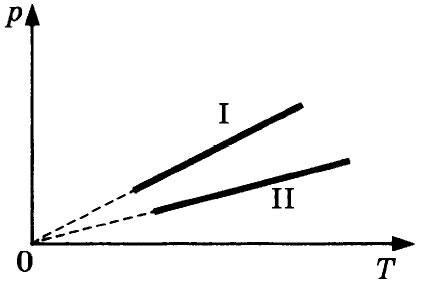
28. Две порции одного и того же идеального газа нагреваются
в сосудах одинакового объёма. Графики процессов представлены на рисунке. Почему изохора I лежит выше изохоры II? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.
1) ν1ν2
2) ν1 = ν2
3) ν1 > ν2
Ответ:
См. РЕШЕНИЕ.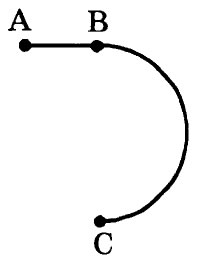
29. Стартуя из точки А (см. рисунок), спортсмен движется равноускоренно
до точки В, после которой модуль скорости спортсмена остаётся постоянным вплоть до точки С. Во сколько раз время, затраченное спортсменом на участок ВС, больше, чем на участок АВ, если модуль ускорения
на обоих участках одинаков? Траектория ВС — полуокружность.
Ответ:
См. РЕШЕНИЕ.
30. Два одинаковых теплоизолированных сосуда соединены короткой трубкой с краном.
Объём каждого сосуда V = 1 м3. В первом сосуде находится ν1 = 1 моль гелия при температуре Т1 = 400 К; во втором ν2 = 3 моль аргона при температуре Т2. Кран открывают.
После установления равновесного состояния давление в сосудах р = 5,4 кПа. Определите
первоначальную температуру аргона Т2.
Ответ:
К См. РЕШЕНИЕ.
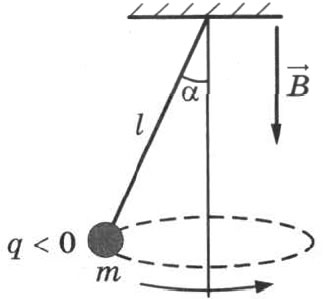
31. В однородном магнитном поле с индукцией В,→направленной вертикально вниз, равномерно вращается по окружности в горизонтальной плоскости против часовой стрелки отрицательно заряженный шарик массой m подвешенный на нити длиной l (конический
маятник). Угол отклонения нити от вертикали равен α, скорость вращения шарика равна
v. Найдите заряд шарика q. Сделайте рисунок с указанием сил, действующих на шарик. Вычислите результат, если B = 1 Тл, l= 71 см, α = 30°, v = 0,5 м/с, m = 1 г.
Ответ:
мКл См. РЕШЕНИЕ.
32. Фотокатод с работой выхода 4,42·10-19 Дж освещается монохроматическим светом. Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией
4·10-4 Тл перпендикулярно линиям индукции этого поля и движутся по окружностям.
Максимальный радиус такой окружности 10 мм. Какова частота ν падающего света?
Ответ:
·1015 Гц См. РЕШЕНИЕ.
Источник