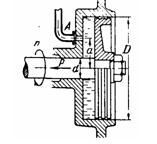
В дне цилиндрического сосуда диаметром
4.1. Найти скорость v течения углекислого газа по трубе, если известно, что за время t= 30 мин через поперечное сечение трубы протекает масса газа m = 0,51 кг. Плотность газа р = 7,5 кг/м3. Диаметр трубы D= 2 см.
Решение:
4.2. В дне цилиндрического сосуда диаметром D= 0,5 м име круглое отверстие диаметром d= 1см. Найти зависимость скорости понижения уровня воды в сосуде от высоты hэтого уровня. Найти значение этой скорости для высоты h= 0,2 м.
Решение:
4.3. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на рас h1 от дна сосуда и на расстоянии h2от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии l от сосуда ( по горизонтали) струя воды падает на стол в случае, если: a) h1= 25 см, h2=16см ; б) h1 =16 см, h2 = 25 см?
Решение:
4.4. Сосуд, наполненный водой, сообщается с атмосферой через стеклянную трубку, закрепленную в горлышке сосуда. Кран К находится на расстоянии h2= 2 см от дна сосуда. Найти скорость v вытекания воды из крана в случае, если расстояние между нижним концом трубки и дном сосуда: а) h1 = 2 см; б) h1 =7,5 см; в) h1 =10 см.
Решение:
4.5. Цилиндрической бак высотой h= 1 м наполнен до краев водой. За какое время t вся вода выльется через отверстие, расположенное у дна бака, если площадь S2поперечного сечения отверстия в 400 раз меньше площади поперечного сечения бака? Сравнить это время с тем, которое понадобилось бы для вытекания того же объема воды, если бы уровень воды в баке поддерживался постоянным на высоте h= 1 м от отверстия.
Решение:
4.6. В сосуд льется вода, причем за единицу времени наливается объем воды V1= 0,2 л/с. Каким должен быть диаметр dотверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне h =8,3 см?
Решение:
4.7. Какое давление р создает компрессор в краскопульте, если струя жидкой краски вылетает из него со скоростью v = 25 м/с? Плотность краски р = 0,8 • 103 кг/м3.
Решение:
4.8. По горизонтальный трубе АВ течет жидкость. Разность уровней этой жидкости в трубах а и bравна dh = 10 см. Диаметры трубок а и bодинаковы. Найти скорость v течения жидкости в трубе АВ.
Решение:
4.9. Воздух продувается через трубку АВ. За единицу времени через трубку АВ протекает объем воздуха V1= 5 л/мин. Площадь поперечного сечения широкой части трубки АВ равна S1 = 2 см2, а узкой ее части и трубки abcравна S2= 0,5 см2. Найти разность уровней dhводы, налитой в трубку abc. Плотность воздуха р = 1,32 кг/м3.
Решение:
4.10. Шарик всплывает с постоянной скоростью v в жид, плотность р1которой в 4 раза больше плоскости мате шарика. Во сколько раз сила трения Fтр , действующая на всплывающий шарик, больше силы тяжести mg, действующей на этот шарик?
Решение:
4.11. Какой наибольшей скорости v может достичь дождевая капля диаметром d= 0,3 мм, если динамическая вязкость воз n= 1,2-10-5 Па*с?
Решение:
4.12. Стальной шарик диаметром d = 1мм падает с посто скоростью v = 0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость nкасторо масла.
Решение:
4.13. Смесь свинцовых дробинок с диаметрами d1 =3 мм и d2= 1 мм опустили в бак с глицерином высотой h= 1 м. На сколько позже упадут на дно дробинки меньшего диаметра по сравнению с дробинками большего диаметра? Динамическая вязкость глицерина n= 1,47 Па*с.
Решение:
4.14. Пробковый шарик радиусом r = 5 мм всплывает в сосуде, наполненном касторовым маслом. Найти динамическую и кинематическую вязкости касторового масла, если шарик всплывает с постоянной скоростью v = 3,5 см/с.
Решение:
4.15. В боковую поверхность цилиндрического сосуда радиусом R = 2 см вставлен горизонтальный капилляр, внутренний радиус r= 1 мм которого и длина l = 2 см. В сосуд налито касторовое масло, динамическая вязкость которого n= 1,2Па*с. Найти зависимость скорости v понижения уровня касторового масла в сосуде от высоты hэтого уровня над капилляром. Найти значение этой скорости при h= 26 см.
Решение:
4.16. В боковую поверхность сосуда вставлен горизон капилляр, внутренний радиус которого r= 1 мм и длина l = 1,5 см. В сосуд налит глицерин, динамическая вязкость которого n= 1,0Па*с. Уровень глицерина в сосуде поддержи постоянным на высоте h = 0,18м выше капилляра. Какое время потребуется на то, чтобы из капилляра вытек объем глицерина V = 5 см3?
Решение:
4.17. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте h1= 5 см от дна сосуда. Внутренний радиус капилляра r =1 мм и длина l = 1 см. В сосуд налито машинное масло, плотность которого р = 0,9 • 103 кг/м3 и динамическая вязкость n = 0,5 Па*с. Уровень масла в сосуде поддерживается постоянным на высоте h2– 50 см выше капилляра. На каком расстоянии Lот конца капилляра (по горизонтали) струя масла падает на стол?
Решение:
4.18. Стальной шарик падает в широком сосуде, напол трансформаторным маслом, плотность которого р — 0,9 • 103 кг/ m3 и динамическая вязкость n= 0,8Па*с. Считая, что закон Стокса имеет место при числе Рейнольдса Re< 0,5 (если при вычислении Reв качестве величины Dвзять диаметр шарика), найти предельное значение диаметра Dшарика.
Решение:
4.19. Считая, что ламинарность движения жидкости (или газа) в цилиндрической трубе сохраняется при числе Рейнольдса Rе<3000 (если при вычислении Reв качестве величины Dвзять диаметр трубы), показать, что условия задачи 4.1 соответствуют ламинарному движению. Кинематическая вязкость газа v = 1,33 • 10-6 м2/с.
Решение:
4.20. Вода течет по трубе, причем за единицу времени через поперечное сечение трубы протекает объем воды V1= 200см3/с. Динамическая вязкость воды n =0,001 Па*с. При каком предельном значении диаметра Dтрубы движение воды остается ламинарным? (Смотри условие предыдущей задачи.)
Решение:
/>
Источник
Задача по физике – 6107
В цилиндрический сосуд высотой $h$ (рис.) через герметичную крышку вертикально вставлена тонкая открытая с двух сторон трубка длиной $L$, немного не доходящая до дна сосуда. В сосуд через трубку наливают жидкость плотности $rho$. Найти высоту уровня жидкости в сосуде в момент, когда трубка полностью заполнится жидкостью. Площадь сечения трубки много меньше площади дна сосуда. Атмосферное давление равно $p_{0}$. Температуру считать постоянной.

Подробнее
Задача по физике – 6108
Вертикальный цилиндрический сосуд сечением $S$ н высотой $H$ заполнен жидкостью плотностью $rho$ и запаян при атмосферном давлении $p_{0}$. При этом высота столба воздуха в сосуде равна $h_{0}$. Какое количество жидкости вытечет из сосуда, если в его нижней части сделать небольшое отверстие? Температура не изменяется.
Подробнее
Задача по физике – 6166
Железная труба имеет длину $l = 10 м$ и толщину стенок $b = 1 см$. Торцы трубы закрыты невесомыми дисками. Из образовавшегося полого цилиндра откачивают воздух. Каким должен быть диаметр $D$ трубы, чтобы она взлетела?
Подробнее
Задача по физике – 6167
В цилиндрический сосуд с площадью два $100 см^{2}$ налита жидкость, плотность которого $rho = 1,2 cdot 10^{3} кг/м^{3}$. В ней плавает кусок льда массой $m = 300 г$. На сколько большее давление испытывает дно сосуда благодаря наличию льда? Как изменится давление на дно, если лед растает? Атмосферное давление не учитывать.
Подробнее
Задача по физике – 6168
К концу однородной палочки, масса которой $M = 4,4 г$, подвешен на нити и алюминиевый шарик радиусом $R = 0,5 см$ (палочку кладут на край стакана с водой, добиваясь такого положения равновесия, при котором погруженной в воду оказывается половина шарика). Определите, а каком отношении делится длина палочки точкой опоры, (рис.)

Подробнее
Задача по физике – 6169
В дне цилиндрического сосуда диаметром $D$ имеете малое круглое отверстие диаметром $d$. Найти зависимость скорости $v_{1}$ понижения уровня воды в сосуде от высоты $h$ этого уровня.
Подробнее
Задача по физике – 6170
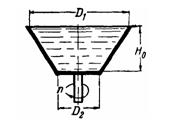
В сосуд имеющий форму прямого кругового усеченного конуса с радиусом дна $R = 10 см$, налита вода так, что ее уровень находится на высоте $h = 10 см$ от дна. Определите силу $F$ давления воды на боковую поверхность сосуда, если образующая конуса составляет угол $alpha = 45^{ circ}$ с его высотой
Подробнее
Задача по физике – 6171
В дно бака, наполненного водой, впаяна труба диаметром $d$, прикрытая сверху цилиндрической пластинкой диаметром $D$ и толщиной $l$ (рис.). Какова должна быть минимальная плотность материала пластинки $rho$, чтобы она не всплывала, если известно, что уровень воды в баке отстоит от верхнею основания пластинки на расстояние $H$. Давление воздуха в трубе равно атмосферному.

Подробнее
Задача по физике – 6172
Какой силы тяжести камень надо положить на плоскую льдину, толщина которой $h = 0,2 м$, чтобы она вместе с камнем полностью погрузилось в воду? Площадь основания льдины $S = 1 м^{2}$, плотность камня $rho_{к} = 2,2 cdot 10^{3} кг/м^{3}$. С какой силой камень давит на льдину?
Подробнее
Задача по физике – 6173
С вышки, расположенной на высоте $h = 1,5 м$ над водой, падает вертикально тонкий алюминиевый стержень данной $l = 50 с$. Какова скорость стержня в момент удара о дно водоема, если глубина водоема у вышки $H = 3 м$? Сопротивлением воздуха и воды движению стержня пренебречь
Подробнее
Задача по физике – 6174
Медный цилиндр диаметром $d = 3 см$ и высотой $h = 20 см$ опущен в воду на тонкой цепочке длиной $l = 1 м$ и массой $m_{1} = 100 г$. Какую минимальную работу нужно совершить, чтобы вынуть цилиндр из воды за цепочку?
Подробнее
Задача по физике – 6176
Круглое отверстие в дне сосуда закрыто конической пробкой с сечением основании $S$ (рис.). При какой наибольшей плотности материала пробки можно, доливая воду, добиться всплытия пробки? Площадь отверстия $S_{0}$.

Подробнее
Задача по физике – 6177
В одинаковых сообщающихся сосудах (рис.) находится вода. Кран К закрыли и воду в правом сосуде нагрели, вследствие чего ее уровень немного повысился. Станет ли вода переливаться из правого сосуда в левый, если открыть кран?

Подробнее
Задача по физике – 6178
В стенке сосуда с водой просверлены одно над другим два отверстия площадью $S = 0,2 см^{2}$ каждое. Расстояние между отверстиями $h_{2} = 50 см$. Уровень воды в сосуде находится на высоте $h_{1} = 30 см$ над верхним отверстием. Найдите точку пересечения струй, вытекающих из отверстий в начальный момент.
Подробнее
Задача по физике – 6179
Площадь поршня в шприце $S_{1} = 1,2 см^{2}$, а площадь отверстия $S_{2} = 1 мм^{2}$. С какой скоростью и сколько времени будет вытекать их шприца жидкость, плотность которой равна $rho$, если ход поршня $l = 4 см$ и на него действуют с силой $F = 5 Н$? Шприц расположен горизонтально.
Подробнее
Источник
В случае равномерного вращения цилиндрического сосуда вокруг вертикальной оси с угловой скоростью ш (рис. 2.25) уравнение любой изобарической поверхности (р = const) имеет вид

где z — координата точки пересечения свободной поверхности с осью вращения;

Изобарические поверхности — параболоиды вращения, ось которых совпадает с осью Oz, а вершины смещены вдоль этой

Рис. 2.25. Вращение цилиндрического сосуда вокруг вертикальной оси оси. Форма изобарических поверхностей не зависит от плотности жидкости.
Изменение давления по вертикали

т.е. такое же, как в неподвижном сосуде.
Пример 2.6. Вертикальный цилиндрический сосуд диаметром D = 40 см и высотой Н = 100 см наполнен до половины водой (рис. 2.26). Определить, с каким предельным числом оборотов можно вращать этот сосуд вокруг сто геометрической вертикальной оси, чтобы из него нс выливалась вода, а также силу давления жидкости на дно сосуда.

Рис. 2.26. Поверхности равного давления во вращающемся сосуде
Решение. Из рис. 2.26 видно, что Н = Zq + h. В соответствии с формулами (2.16) и (2.17)

Тогда

Начальный уровень Л0 в резервуаре по условию равен Н/2. Следовательно,

Соответственно

Предельное число оборотов
 (об/мин).
(об/мин).
Для определения силы давления жидкости на дно сосуда найдем распределение избыточного давления, полагая р0 = р ‘.

Координату z0 вершины параболоида определим по формуле
 т.с. параболоид свободной поверхности касается дна сосуда. Тогда
т.с. параболоид свободной поверхности касается дна сосуда. Тогда

Для точек на дне сосуда (z = 0) избыточное давление определим следующим образом:

Силу давления на дно сосуда найдем как сумму элементарных сил давления, действующих на элементарные кольцевые площадки, равные 2nrdr.

Задачи для самостоятельного решения
- 2.18. Призматический сосуд дайной 3 м и шириной 1 м, перемещающийся горизонтально с постоянным ускорением 0,4g, разделен на два отсека, заполненных водой до высот 1 м и 1,75 м соответственно. Определить результирующую силу давления воды на перегородку, разделяющую отсеки.
- 2.19. Измеритель ускорения тела, движущегося горизонтально, представляет собой закрепленную на нем U-образную трубку малого диаметра, наполненную жидкостью. Определить, с каким ускорением движется тело, если при движении в коленах измерителя установилась разность уровней жидкости 75 мм при расстоянии между уровнями 250 мм.

Рис. 2.27. К определению поверхности равного давления при равномерном вращении сосуда с жидкостью

Рис. 2.28. К определению относительного равновесия жидкости в закрытом равномерно вращающемся сосуде
2.20. Сосуд, имеющий форму усеченного конуса, заполнен водой до половины высоты и приводится во вращение вокруг своей вертикальной оси (рис. 2.27). Определить наибольшее число оборотов, при котором вода не будет выливаться из сосуда, если И =
= а = 0,8 м и угол а = 45°.
- 2.21. Закрытый цилиндрический сосуд, радиус которого г, = 50 см, равномерно вращается относительно вертикальной оси. При этом уровень жидкости в открытой трубке малого диаметра, установленной на расстоянии г2 = 35 см от центра, расположен на высоте И =
- 40 см (рис. 2.28). Плотность жидкости равна 800 кг/м3; атмосферное давление 760 мм рт. ст. Определить наибольшую
угловую скорость, при которой сохранится относительное равновесие жидкости. Давление насыщенных паров жидкости равно 49 кПа[1].
2.22. Закрытый сверху крышкой цилиндр диаметром 0,9 м и высотой 0,8 м содержит 0,35 м3 воды и вращается вокруг вертикальной оси с угловой скоростью 100 с1. Определить усилия, действующие при этом на крышку цилиндра, если давление на поверхности воды атмосферное.
Источник
Часть 4-1 Равновесие жидкости в движущихся сосудах
Задача (Куколевский И.И.) 4-1. Для измерения ускорения горизонтально движущегося тела может быть использована закрепленная на нем U-образная трубка малого диаметра, наполненная жидкостью. С каким ускорением движется тело, если при движении установилась разность уровней жидкости в ветвях трубки, равная h = 5 см при расстоянии между ними l = 30 см?
Ответ. а = 1,635 м/с2.
Скачать решение задачи 4-1 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-2. Призматический сосуд длиной 3*l = 3 м и шириной с = 1 м, перемещающийся горизонтально с постоянным ускорением а =0,4g, разделен на два отсека, заполненных водой до высот h1 = 1 м и h2 = 1,75л.
1) Определить cуммарную силу давления P воды на перегородку.
2) Найти ускорение, при котором эта сила станет равной нулю.
Ответ. 1) Р = 2,17 кН.2) а = 0,5g.
Скачать решение задачи 4-2 (Куколевский И.И.) (цена 80р)
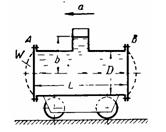
Задача (Куколевский И.И.) 4-3. Цистерна диаметром D = 1,2 м и длиной L = 2,5 м, наполненная нефтью (δ = 0,9) до высоты b = 1 л, движется горизонтально с постоянным ускорением а = 2 м/с2.
1) Определить силы давления на плоские боковые крышки А и В цистерны.
2) Как изменятся эти силы при замене плоских крышек сферическими. Увеличение объема цистерны при такой замене равно 2W, где W = 0,2 м3.
Ответ 1) PА = 7,42 кН. РB = 12,5 кН; 2) Р’А = 7,3 кН; Р’В = 13 кН.
Скачать решение задачи 4-3 (Куколевский И.И.) (цена 80р)
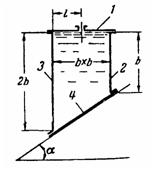
Задача (Куколевский И.И.) 4-4. По наклоненной под углом а = 45° к горизонту плоскости под действием силы тяжести скользит призматический сосуд, целиком заполненный водой. Сосуд закрыт крышкой с малым отверстием, расположенным на расстоянии l = 0,5 м от передней стенки. Собственный вес сосуда G=150 кГ, размер b=1 м, коэффициент трения дна сосуда о плоскость скольжения f= 0,278. Найти величины сил давления воды на крышку 1, стенки 2 и 3, дно 4, считая, что жидкость из сосуда не выливается.
Ответ. P1=0 Р2=4,9 кН; P3 = 8,98 кН; Р4 =13,3 кН.
Скачать решение задачи 4-4 (Куколевский И.И.) (цена 80р)
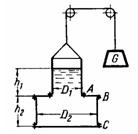
Задача (Куколевский И.И.) 4-5. Составной цилиндрический сосуд, заполненный водой до высоты h1+h2 = 800 мм, подвешен на шнуре, перекинутом через блоки, и соединен с грузом массой m = 200 кг. Определить нагрузки болтовых групп А, В и С при имеющем место ускоренном движении сосуда. Размеры сосуда D1 = 400 мм, D2=600 мм, h1 = 300 мм. Собственным весом сосуда и трением в блоках пренебречь.
Ответ. РА1= 1,67 кН; РВ = PС= 2,56 кН.
Скачать решение задачи 4-5 (Куколевский И.И.) (цена 80р)
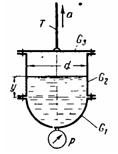
Задача (Куколевский И.И.) 4-6. Цилиндрический сосуд диаметром d = 0,8 м, имеющий плоскую крышку и полусферическое дно, заполнен водой до высоты у =0,3 ми поднимается вертикально вверх с ускорением а =10 м/с2.
1) Определить усилие Т в тяге, если вес дна сосуда m1 = 50 кк, цилиндрической части m2 = 30 кг и крышки m3 = 20 кu.
2) Силу давления на дно сосуда, если вакуумметр, присоединенный к нижней точке сосуда, показывал V = 30 кПа, когда сосуд был неподвижен.
3) Построить эпюру давления жидкости по высоте в неподвижном сосуде и при ускоренном его движении.
Ответ. 1) Т = 7,63 кН. 2) P = 12,9 кН.
Скачать решение задачи 4-6 (Куколевский И.И.) (цена 80р)
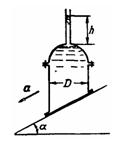
Задача (Куколевский И.И.) 4-7. Вычислить величины горизонтальной и вертикальной сил давления на полусфгрическую крышку цилиндрического сосуда диаметром D = 0,6 м, скользящего с ускорением а = 5 м/с2 по плоскости, наклоненной под углом а = 60° к горизонту, если сосуд заполнен водой до уровня h=1 м в открытой трубке, присоединенной к верхней точке сосуда. Как изменятся эти силы, если сосуд остановить?
Ответ. Рв = 1700Н, Рг = 141 Н. Для неподвижного сосуда Рв = 3050 Н; Рг=0
Скачать решение задачи 4-7 (Куколевский И.И.) (цена 80р)
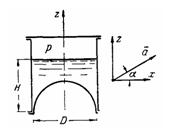
Задача (Куколевский И.И.) 4-8. Закрытый цилиндрический сосуд диаметром D = 0,6 м, имеющий полусферическое дно, наполнен до уровня H = 0,8 м водой и движется прямолинейно под углом а = 30° к горизонту с постоянным ускорением а = 2g. Определить вертикальную и горизонтальную силы давления на дно, если избыточное давление газа лад поверхностью воды в сосуде Рн = 20 кПа.
Ответ. Рв = 8980 Н; Рг = 960 Н.
Скачать решение задачи 4-8 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-9. Найти зависимость показания h водяного манометра (радиусы ветвей R1 и R2 заданы), присоединенного к замкнутому сосуду, который наполнен газом, находящимся под вакуумом Pв, от: 1) поступательного ускорения сосуда (а), направленного по вертикали вверх и вниз; 2) угловой скорости вращения сосуда (w).
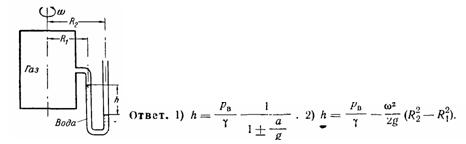
Скачать решение задачи 4-9 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-10. Цилиндрический сосуд, заполненный водой, приведен во вращение с постоянной угловой скоростью w = 10 рад/с. Найти наименьшее давление в воде, заполняющей сосуд, по показанию h= 1 м ртутного манометра, вращающегося вместе с сосудом, если r1 = 0,8 м; r2 = 0,7 м. При какой угловой скорости равновесие жидкости в сосуде нарушится?
Ответ. 1) р=3 кПа. 2) w=13,2 рад/с.
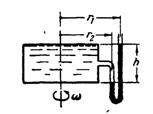
Скачать решение задачи 4-10 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-11. Вал жидкостного тахометра вращает диск, который увлекает во вращательное движение масло, находящееся в нижней полости корпуса прибора, куда оно поступает из верхней полости через радиальные отверстия полого вала. Создающееся в нижней полости повышенное за счет вращения давление измеряется пьезометром.
Определить высоту Н шкалы пьезометра, необходимую для измерения числа оборотов вала тахометра n = 300 об/мин, если диаметр диска D = 0,2 м. Влиянием зазора между диском и корпусом прибора пренебречь.
Ответ. H= 0,504 м.
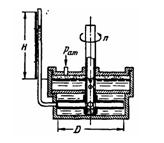
Скачать решение задачи 4-11 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-12. Цилиндрический сосуд с закраиной, имеющий диаметр D = 400 мм и высоту H = 300 мм. предварительно целиком заполненный жидкостью, равномерно вращается относительно вертикальной оси, делая 200 об/мин. Какой объем жидкости может удержаться в сосуде при данном числе оборотов, если диаметр закраины d = 200 мм? Какой наибольший объем жидкости удержится в сосуде при сколь угодно большом числе оборотов?
Ответ W1=34,2л, W2= 28,3 л.
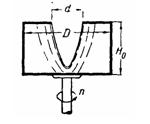
Скачать решение задачи 4-12 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-13. Найти число оборотов цилиндрического сосуда высотой H0 = 1,2 м и диаметром D = 0,8м, наполненного жидкостью до высоты H0/2, при котором жидкость поднимется до краев сосуда. Определить число оборотов сосуда, при котором в нем останется лишь половина первоначального объема жидкости.
Ответ, n1= 116 об/мин. n2 = 163,5 об/мин.
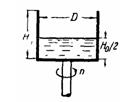
Скачать решение задачи 4-13 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-14. Тормозной шкив диаметром D1 = 800 мм и высотой H0=200 мм, вращающийся относительно вертикальной оси при n=120 об/мин, наполнен охлаждающей водой до предела, соответствующего данному числу оборотов.
1) Определить радиус rх сухой части дна, если D2 = 500 мм.
2) Силы, приложенные к верхнему и нижнему днищам.
3) На какой высоте х установится вода после остановки шкива.
Ответ. 1) rх = 194 мм. 2) Р1= 1180 Н; Р2= 1850 Н. 3) r = 137 мм.

Скачать решение задачи 4-14 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-15. Замкнутый цилиндр размерами R= 0,4 лг и H0 = 0,7 м содержит воду в количестве W = 0,25 м3 и вращается относительно вертикальной оси с угловой скоростью w = 10; 20 и 100 рад/с. Определить усилия, действующие при указанных оборотах на крышку цилиндра, если давление над водой равно атмосферному.
. Ответ. Р = 0,176 кН; 2,9 кН и 100 кН
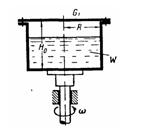
Скачать решение задачи 4-15 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-16. Цилиндрический сосуд диаметром D = 690 мм и высотой H0 = 500 мм заполнен водой до Н = 400 мм. Остальной объем сосуда заполнен маслом (δ=0,8). Сосуд закрыт крышкой с малым отверстием в центре и приведен во вращение относительно центральной вертикальной оси. Определить, с какой угловой скоростью ш нужно вращать сосуд для того, чтобы поверхность раздела жидкостей коснулась дна сосуда. Найти усилия, действующие при этом на дно и крышку сосуда.
Ответ. w= 16,5 рад/с; Pкр = 1,51 кН; Рдно = 2,84 кН.
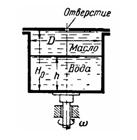
Скачать решение задачи 4-16 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-17. Цилиндрический сосуд диаметром D = 1,2 м, наполненный водой до высоты а = 0,6м в пьезометрах одинакового диаметра, установленных на крышке сосуда на расстояниях r1 = 0,2 м и r2 = 0,4 м от оси, вращается с числом оборотов n = 60 об/мин. Определить силу давления на крышку сосуда и указать, как она будет меняться качественно, если поочередно выключать пьезометры.
Ответ. Р = 8450 Н.
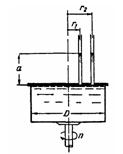
Скачать решение задачи 4-17 (Куколевский И.И.) (цена 80р)
Часть 4-2 Равновесие жидкости в движущихся сосудах
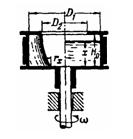
Задача (Куколевский И.И.) 4-18. Изображенный на чертеже сосуд имеет размеры D = 0,4 м; d = 0,2 м, b = 0,35 м и наполнен водой до высоты а+b = 0,52 м. Сверху сосуд закрыт поршнем, масса которого m = 50 кг. Определить гидравлические нагрузки болтовых групп А и В, если сосуд вращается относительно центральной вертикальной оси с числом оборотов n = 450 об/мин. Трением между поршнем и стенками цилиндра пренебречь.
Указание. При вращении системы суммарная сила давления жидкости на поршень равна весу поршня. Это условие позволяет найти давление в центре поршня и, следовательно, во всех точках сосуда.
Ответ. РА=РВ = 3710 Н.
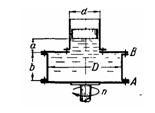
Скачать решение задачи 4-18 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-19. Жидкостный тахометр состоит из цилиндра, наполненного ртутью и сообщенного с двумя трубками малого диаметра d, расположенными на расстоянии R от оси. Цилиндр снабжен поршнем, имеющим диаметр D. Поршень перемещается при изменении числа оборотов тахометра. Установить связь между числом оборотов n тахометра и опусканием h поршня от его начального положения при невращающемся тахометре.
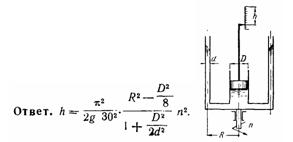
Скачать решение задачи 4-19 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-20. В жидкости, плотность которой ρ, удерживается в равновесии тело плотностью ρ1. Определить, какое начальное ускорение a0, по отношению к жидкости приобретет тело, если его освободить, при условии., что: 1) сосуд, содержащий жидкость, неподвижен; 2) сосуд движется вертикально (вверх или вниз) с постоянным ускорением а; 3) сосуд равномерно вращается относительно вертикальной оси с угловой скоростью w; 4) сосуд движется горизонтально с постоянным ускорением а.
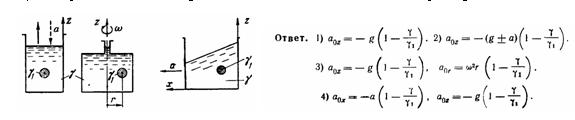
Скачать решение задачи 4-20 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-21. Определить минимальное число оборотов литейной формы, при котором легкие включения имеют возможность выделиться из расплавленного металла в середину формы, при следующих размерах отливаемой детали: D1 = 300 мм; D2 = 200 мм; Н = 300 мм.
Указание. Условия относительного движения легкой частицы во вращающейся литейной форме определяются действием на нее сил давления жидкого металла Р, собственного веса частицы G и переносной силы инерции J. Направление результирующей К этих сил обеспечивает при любом числе оборотов перемещение легких включений по внутреннему наклонному и горизонтальному каналам формы к ее центру. По внешнему наклонному каналу (см. рис. к задаче 4-21) легкие включения могут перемещаться к центру формы лишь в том случае, когда результирующая R имеет составляющую, направленную вдоль стенки вниз.
Ответ, n = 231 об/мин.
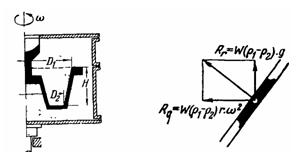
Скачать решение задачи 4-21 (Куколевский И.И.) (цена 80р)
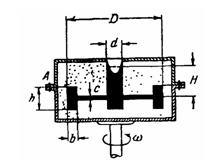
Задача (Куколевский И.И.) 4.22 Отливка чугунного колеса диаметром D = 1000 мм, с ободом высотой h = 200 мм и толщиной d = 80 мм, диском толщиной с = 40 мм и ступицей диаметром d = 200 мм производится во вращающуюся с n = 200 об/мин земляную форму. Определить растягивающую силу в болтовой группе А опоки, не учитывая веса опоки и земли. Высота заполнения формы Н = 300 мм, плотность жидкого чугуна у = 7200 кг/м3.
Ответ. РА = 167 кН.
Задача (Куколевский И.И.) 4-23. Определить силу давления на коническую боковую поверхность АВС и плоское дно АС сосуда, целиком заполненного водой и вращающегося с угловой скоростью wо = 20 рад/с, если известно, что в верхней точке В сосуда вакуум равен рв = 20 кПа. Размеры сосуда: D=1 м; а = 1 м.
Ответ. РАВС = 9,38 кН; РАС = I 2 кН.
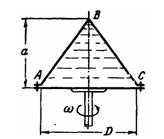
Скачать решение задачи 4-23 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-24. Определить наименьшее число оборотов, при котором полностью опорожнится предварительно заполненный жидкостью Открытый конический сосуд, имеющий диаметры D1 = 460 мм; D2 = 200 мм и высоту H0 = 75 мм. Указание. Полное опорожнение сосуда произойдет при таком числе оборотов, когда свободная поверхность жидкости коснется стенки сосуда у его дна и вектор суммарной массовой силы, действующей на последнюю частицу жидкости в этой точке, окажется нормальным к стенке.
Ответ. n = 71,7 об /мин.
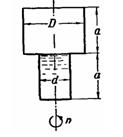
Задача (Куколевский И.И.) 4-25. Сосуд, вращающийся относительно вертикальной оси, состоит из двух цилиндров одинаковой высоты а = 200 мм и диаметров d=150 мм. и D = 300 мм. Нижний цилиндр целиком заполнен жидкостью. При каком числе оборотов жидкость начнет выливаться из сосуда? Отметить качественное влияние размеров а, d и D сосуда на искомое число оборотов.
Ответ, n = 252 об /мин.
Скачать решение задачи 4-25 (Куколевский И.И.) (цена 80р)
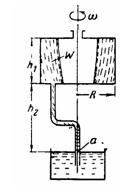
Задача (Куколевский И.И.) 4-26. Цилиндрический сосуд радиуса R = 250 мм и высоты h1 = 300 мм, заполненный объемом жидкости W = 45 дм3, вращается относительно центральной вертикальной оси. Ко дну сосуда присоединена изогнутая трубка, ось нижнего конца которой совпадает с осью вращения сосуда. Конец трубки опущен под уровень неподвижной жидкости, расположенный ниже дна верхнего сосуда на h2 = 460 мм.
1) Определить угловую скорость w* вращения сосуда, при которой жидкость во вращающейся трубке находится в относительном покое.
2) Выяснить направление движения жидкости в трубке при w>< w*. Указание. Относительный покой жидкости в трубке возможен только при условии, что давление в точке а трубки на уровне свободной поверхности в неподвижном сосуде равно атмосферному и что, следовательно, вершина параболоида пьезометрической поверхности проходит через эту точку
Ответ, w*=30 рад/с
Задача (Куколевский И.И.) 4-27. Гидравлическая пята, вращающаяся с числом оборотов n = 3000 об/мин, получает воду по трубке А под давлением р= 10 атм. Определить осевую силу Р, которую может уравновешивать пята, считая, что вода под поршнем вращается с половиной угловой скорости вращения последнего. Диаметр поршня D = 0,32 м, диаметр вала d = 0,05 м, трубка присоединена к корпусу пяты на расстоянии а = 0,07 м от оси. На каком расстоянии от оси нужно расположить трубку А, чтобы осевая сила, уравновешиваемая пятой, не зависела от оборотов?
Ответ. Р = 86 кН, а =0,113 м.