В два одинаковых сосуда поперечное сечение которых 10

4.2. Элементы гидростатики

4.2.5. Сообщающиеся сосуды

Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.

Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:

h1h2=ρ2ρ1,

где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.

Указанный закон справедлив в отсутствие сил поверхностного натяжения.

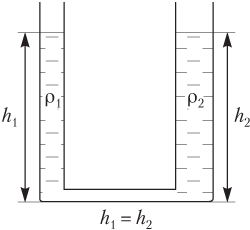
Если сообщающиеся сосуды заполнены однородной жидкостью

ρ1 = ρ2,

то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):

h1 = h2,

где h1 — высота столба жидкости в левом колене; h2 — высота столба жидкости в правом колене сообщающихся сосудов.

Рис. 4.14

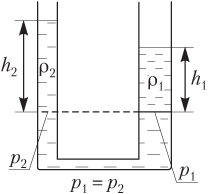
Если сообщающиеся сосуды заполнены разнородными жидкостями

ρ1 ≠ ρ2,

то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение

h1h2=ρ2ρ1,

где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.

Рис. 4.15

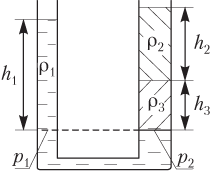
Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой

p1 = ρ1gh1,

в правом колене —

p2 = ρ2gh2 + ρ3gh3.

Рис. 4.16

Равенство давлений на указанном уровне

p1 = p2

позволяет записать тождество:

ρ1h1 = ρ2h2 + ρ3h3.

Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.

Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.

Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:

• в первом сосуде оказывается масса жидкости

m1 = ρV1 = ρ∆h1S1,

где ρ — плотность жидкости; V1 = S1∆h1 — объем жидкости в первом сосуде; S1 — площадь поперечного сечения первого сосуда; ∆h1 — повышение уровня жидкости в первом сосуде;

• во втором сосуде оказывается масса жидкости

m2 = ρV2 = ρ∆h2S2,

где V2 = S2∆h2 — объем жидкости во втором сосуде; S2 — площадь поперечного сечения второго сосуда; ∆h2 — повышение уровня жидкости во втором сосуде.

Повышение уровней жидкости в обоих сосудах одинаково:

∆h1 = ∆h2 = ∆h,

поэтому масса жидкости, добавленной в систему, определяется формулой

m = m1 + m2 = ρ∆h(S1 + S2).

Выразим отсюда искомое значение ∆h:

Δh=mρ(S1+S2).

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для первого (широкого) сосуда

S1=πd124,

• для второго (узкого) сосуда

S2=πd224,

где d1 = 2d2 — диаметр первого (широкого) сосуда; d2 — диаметр второго (узкого) сосуда.

Отношение площадей

S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4

позволяет найти площадь широкого сосуда:

S1 = 4S2.

Подставив S1 в формулу для ∆h

Δh=mρ(4S2+S2)=m5ρS2,

рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:

Δh=0,125⋅1,6⋅103⋅10⋅10−4=15⋅10−3 м=15 мм.

Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем — 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.

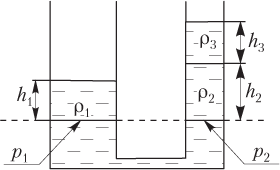
Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:

p1 = p2,

где p1 — давление в широком сосуде; p2 — давление в узком сосуде.

На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.

Гидростатическое давление на выбранном уровне:

• в широком сосуде

p1 = ρ1gh1,

где ρ1 — плотность жидкости, заполняющей систему изначально; g — модуль ускорения свободного падения; h1 — высота столба жидкости в широком сосуде;

• в узком сосуде

p2 = ρ2gh2 + ρ3gh3,

где ρ2 — плотность первой жидкости, добавленной в узкий сосуд; h2 — высота столба первой жидкости; ρ3 — плотность второй жидкости, добавленной в узкий сосуд; h3 — высота столба второй жидкости.

Равенство давлений на указанном уровне

ρ1gh1 = ρ2gh2 + ρ3gh3

позволяет определить высоту столба жидкости в широком сосуде:

h1=1ρ1(ρ2h2+ρ3h3),

где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:

• для первой жидкости

h2=m2ρ2S2;

• для второй жидкости

h3=m3ρ3S2,

где S2 — площадь поперечного сечения узкого сосуда; m2 — масса первой жидкости, добавленной в узкий сосуд; m3 — масса второй жидкости, добавленной в узкий сосуд.

Подстановка h2 и h3 в формулу для h1 дает

h1=1ρ1(ρ2m2ρ2S2+ρ3m3ρ3S2)=m2+m3ρ1S2.

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для широкого сосуда

S1=πd124,

• для узкого сосуда

S2=πd224,

где d1 = 2d2 — диаметр широкого сосуда; d2 — диаметр узкого сосуда.

Отношение площадей

S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4

позволяет найти площадь узкого сосуда:

S2=S14.

Таким образом, высота столба жидкости в широком сосуде определяется выражением

h1=4(m2+m3)ρ1S1.

Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:

h2+h3=m2ρ2S2+m3ρ3S2=4S1(m2ρ2+m3ρ3).

Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле

Δh=(h2+h3)−h1=4S1(m2ρ2+m3ρ3)−4(m2+m3)ρ1S1=

=4S1(m2ρ2+m3ρ3−(m2+m3)ρ1).

Произведем вычисление:

Δh=410⋅10−4(0,122,0⋅103+0,124,0⋅103−0,12+0,126,0⋅103)=0,20 м=20 см.