В двух сосудах находилось 600 г и 150 г
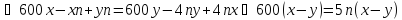
РТ 2004 В9.Влажность фруктов 80%, а сухофруктов 24%. Сколько нужно фруктов, чтобы получить 5 кг сухофруктов?
Решение
Пусть кг нужно фруктов, чтобы получить 5 кг сухофруктов.
В кг фруктов содержитсякг воды. В 5 кг сухофруктов содержитсякг воды.
Если из сухофруктов и фруктов удалить всю воду, то получим равные количества:
Ответ: 19.
Сканави 13.379 (5 изд) Цена бриллианта пропорциональна квадрату его массы. Бриллиант массойкарат был разбит на две части, после чего его стоимость уменьшилась враз. Найдите массу частей, на которые был разбит бриллиант. Доказать, что наибольшая потеря в стоимости бриллианта происходит в том случае, когда обе его части равны по массе.
Решение
Пусть и- масса первой и второй части соответственно,- коэффициент пропорциональности цены к массе. Составляем систему.
Из последнего уравнения системы получаем ., т.к. дискриминант должен быть неотрицательным, то наибольшее, при котором дискриминант неотрицателен, равен 2.
Ответ: ,.
РТ 3 2007 В8.Пусть стоимость алмаза пропорциональна квадрату его массы. При огранке алмаз раскололся на две части. Стоимость одной из частей оказалась на 98,79% меньше, чем первоначальная стоимость алмаза. Найдите, сколько процентов от первоначальной массы алмаза составляет масса этой части.
Решение
Фраза «стоимость алмаза пропорциональна квадрату его массы» формализуется так: пусть ― масса алмаза, тогда― его стоимость, где― коэффициент пропорциональности.
Фраза «при огранке алмаз раскололся на 2 части» формализуется так: ― масса одной из частей алмаза (пусть это будет первая часть),― стоимость этой части алмаза.
Фраза «стоимость первой части оказалась на 98,56 % меньше, чем первоначальная стоимость алмаза» формируется так: ― стоимость первой часть алмаза.
Завершается условие задачи вопросом «сколько процентов от первоначальной массы алмаза составляет масса первой части?», т.е. требуется найти .
Среди составленных алгебраических выражений имеются два, означающих одну и ту же величину (стоимость первой части алмаза): и.Приравняем их и упростим полученное уравнение:. Отсюда искомая величинаравна 11.
Ответ: 11.
РТ 1 2010 В2.Однозначное число увеличили на 8 единиц. Если полученное число увеличить на столько же процентов, как и в первый раз, то получится 36. Найдите первоначальное число.
Решение
Фраза/переформулировка | Математическая модель |
Однозначное число | |
увеличили на 8 единиц. | |
на сколько процентов оно увеличилось | |
Т.е. число выросло в раза | |
Если полученное число увеличить на столько же процентов (во столько же раз), как и в первый раз, | |
то получится 36. | |
Найдите первоначальное число. | |
Ответ: 4.
Задачи на смеси и концентрации(all done)
ЦТ 2006 B8.Два сосуда равных объёмов до краёв заполнены раствором кислоты равной концентрации. Из первого сосуда отлили 1 л раствора и долили 1 л воды. Потом эту же процедуру повторили ещё раз. Из второго сосуда отлили 3 л раствора и долили 3 л воды. Потом эту же процедуру повторили ещё раз. В результате концентрация кислоты в первом сосуде стала в 1,96 раза больше, чем во втором. Найдите объём сосуда (в литрах).
Решение
Пусть – объем сосуда. По условию задачи. Пусть- первоначальная концентрация кислоты в растворе, тогда- концентрация кислоты, после первой процедуры в первом сосуде.- концентрация кислоты после второй процедуры. По аналогии, после второй процедуры, концентрация кислоты во втором сосуде -.
Получаем уравнение:
.Второй корень посторонний.
Ответ: 8.
РТ 1 2008 В8.В двух сосудах находилось 600 г и 150 г растворов соли различной концентрации. Из каждого сосуда взяли одновременно пограммов раствора. Взятое из первого вылили во второй, а взятое из второго – в первый. После этого концентрация растворов в обоих сосудах стала одинаковой. Найдите.
Решение
Фраза | Математическая модель | |||
I сосуд | II сосуд | |||
концентрация | масса соли | концентрация | масса соли | |
В двух сосудах находилось 600 г и 150 г растворов соли различной концентрации. | ||||
Из каждого сосуда взяли одновременно по граммов раствора. | ||||
Взятое из первого вылили во второй, а взятое из второго – в первый. | ||||
После этого концентрация растворов в обоих сосудах стала одинаковой. | ||||
Найдите . | По условию концентрация различная, значит , и получаем равносильное уравнение. | |||
Ответ: 120.
ЦТ 2012 В11. Из двух растворов с различным процентным содержанием спирта массой 100 г и 900 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Решается аналогично.
Источник
ЗАДАЧИ НА СМЕСИ, СПЛАВЫ И РАСТВОРЫ
ПОВТОРИМ: 1) Представим в виде дроби проценты: а) 50% б) 43% в)125% г) 4, 2% 50% = 0, 5, 43% = 0, 43, 125% = 1, 25, 4, 2% = 0, 042 2) Отношение чисел – это частное этих чисел. Найти отношение числа 20 к 80 20 : 80 = 0, 25 или ¼. 3) Нахождение дроби от числа: чтобы найти дробь от числа, надо дробь умножить на число. 0, 3 от 70 находится так: 0, 3 · 70 = 21 3) Решение линейного уравнения: 0, 25 х + 0, 13 (х+5) = 0, 2 (2 х+5)
Возьмем 180 граммов воды и добавим в воду 20 граммов соли. Получим раствор соли, его масса равна 180 + 20 = 200 граммов. Концентрация соли (процентное содержание соли) – это отношение количества соли к количеству раствора, записанное в процентах (20 : 200) ·100 = 10%
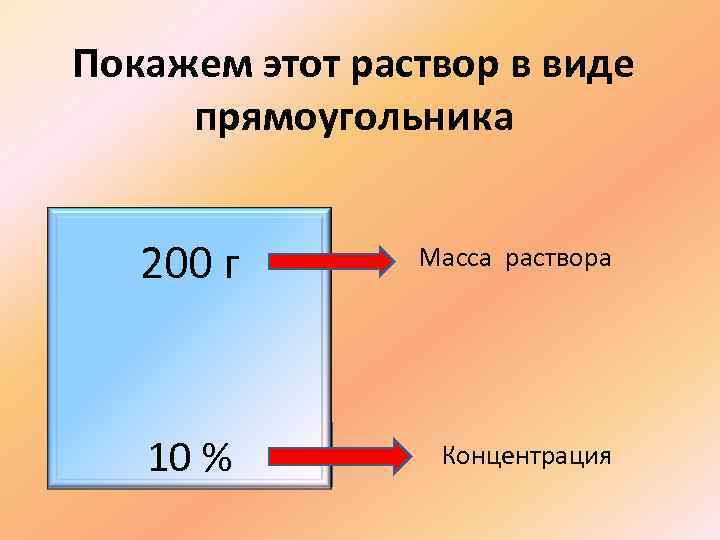Покажем этот раствор в виде прямоугольника 200 г Масса раствора Концентрация 10 %
Возьмем 15 кг цемента и 45 кг песка, высыпаем содержимое ведер в ящик и тщательно перемешаем цемент с песком. Получим смесь цемента с песком, её масса равна 15 кг + 45 кг = 60 кг. Концентрация цемента (процентное содержание цемента) – это отношение количества цемента к количеству смеси, записанное в процентах – (15 : 60)· 100 = 25%
Покажем эту смесь в виде прямоугольника 60 кг 25 %
• смешали, перемешали: «+» • отлили: «-» • долили, добавили: «+»
Закон сохранения объема или массы Если два сплава (раствора) соединяют в один «новый» сплав (раствор), то V = V 1 + V 2 – сохраняется объем; m = m 1+ m 2 – сохраняется масса. Причем сохраняется масса не только раствора, но и чистого вещества.
Например, смешали раствор воды с песком, в котором 4 кг песка и 10 кг воды, с другим раствором, в котором 10 кг песка и 20 кг воды. Какова масса полученного раствора? (44 кг) Какова масса песка в полученном растворе? (14 кг)
Задача № 1 Имеется 30 кг 26%-го раствора соли. Требуется получить 40%-ый раствор соли. Сколько килограммов 50%-го раствора добавить? соли нужно
Задача № 1 Имеется 30 кг 26%-го раствора соли. Требуется получить 40%-ый раствор соли. Сколько килограммов 50%-го раствора соли нужно добавить? Имеется Нужно добавить Требуется получить 30 кг + 26 % х кг (30+х )кг = 50 % 40 %
Имеется 30 кг 26%-го раствора соли. Требуется получить 40%-ый раствор соли. Сколько килограммов 50%-го раствора соли нужно добавить? 30 кг х кг (30+х )кг = 0, 26 + 30· 0, 26 + х · 0, 5 = 30· 26 + х· 50 = (30+х)· 40 0, 5 0, 4 (30+х)· 0, 4
Таким образом, алгоритм составления уравнения следующий: по вертикали из каждого прямоугольника находим массу чистого вещества, умножив массу или объем на концентрацию; по горизонтали составляем уравнение согласно действиям в схеме.
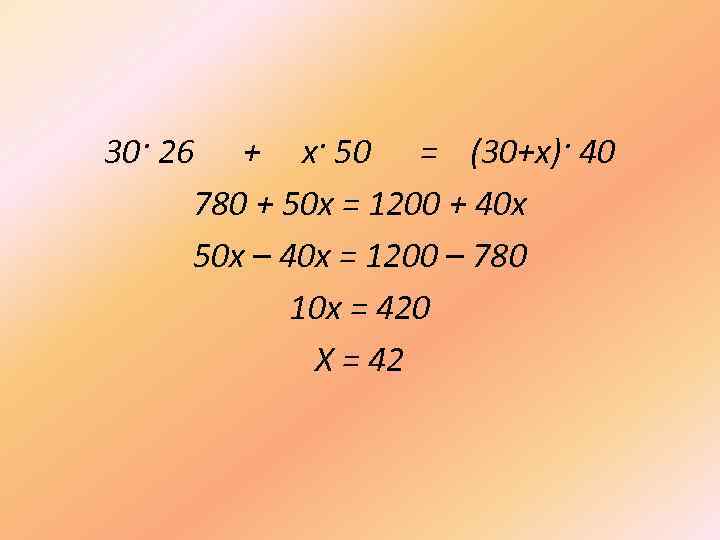30· 26 + х· 50 = (30+х)· 40 780 + 50 х = 1200 + 40 х 50 х – 40 х = 1200 – 780 10 х = 420 Х = 42
Задача № 2 В бидоне было 3 литра молока 6%-ой жирности. После того как в бидон добавили некоторое количество молока 2%-ой жирности и тщательно перемешали, получили молоко с жирностью 3, 2%. Сколько литров молока 2%-ой жирности было добавлено в бидон?
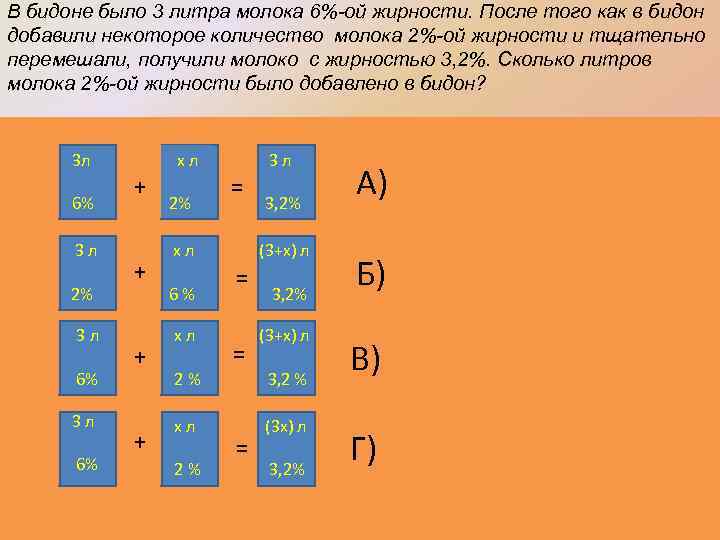В бидоне было 3 литра молока 6%-ой жирности. После того как в бидон добавили некоторое количество молока 2%-ой жирности и тщательно перемешали, получили молоко с жирностью 3, 2%. Сколько литров молока 2%-ой жирности было добавлено в бидон? 6% 3 л 2% 3 л 6% х л + + 2% 3 л = х л 6 % х л 2 % 3, 2% (3+х) л = = 3 л = 3, 2% (3+х) л 3, 2 % (3 х) л 3, 2% А) Б) В) Г)
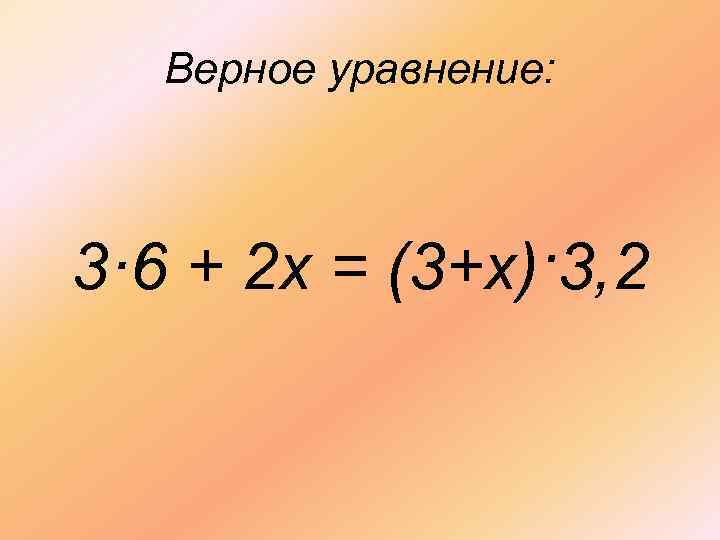Верное уравнение: 3· 6 + 2 х = (3+х)·3, 2
Задача № 3 Из чаши, содержащей 300 граммов 6%-го раствора уксусной кислоты, отлили некоторое количество этого раствора и добавили такое же количество воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты.
Было Отлили Добавили Получили
Из чаши, содержащей 300 граммов 6%-го раствора уксусной кислоты, отлили некоторое количество этого раствора и добавили такое же количество воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты. Было Отлили х г 6% Получили 300 г 6% Добавили х г + 300 г = 0% 2% 300 · 6 – 6 х + х· 0 = 300 · 2 Ответ: 200 г.
Задача № 4 •
•
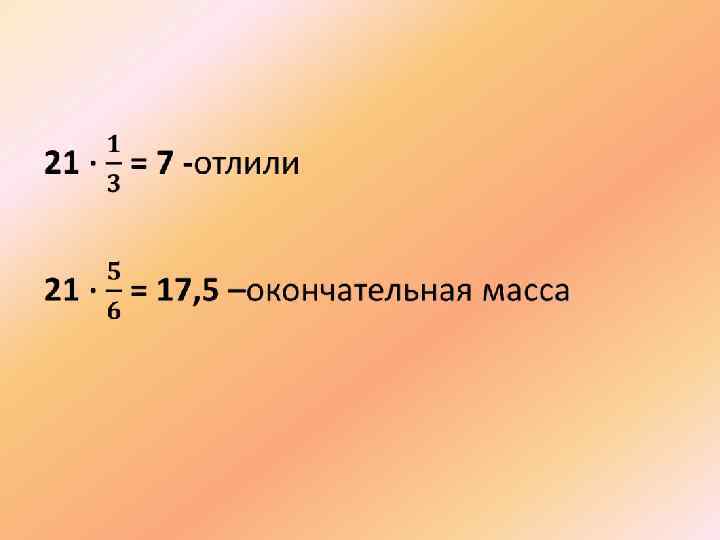21 л 10% 7 л – = + 10% 0% 17, 5 л х%
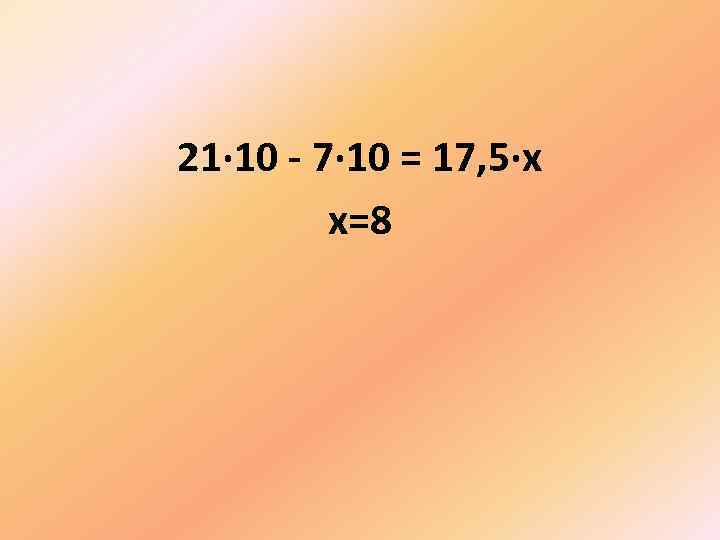21· 10 – 7· 10 = 17, 5·х х=8
Задача № 5 Имеется кусок сплава меди с оловом общей массой 24 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40% меди?
Имеется кусок сплава меди с оловом общей массой 24 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40% меди? 24 кг 45% х кг + 0% 24+х = 24 · 45 + х · 0 = 40(24 + х) х = 3 40%
Задача № 6 К раствору соляной кислоты добавили 100 г соляной кислоты. В результате получили 600 г 18%-го раствора соляной кислоты. Сколько граммов соляной кислоты растворе? содержалось в исходном
К раствору соляной кислоты добавили 100 г соляной кислоты. В результате получили 600 г 18%-го раствора соляной кислоты. Сколько граммов соляной кислоты содержалось в исходном растворе? 500 г Х% + 100 г 100% 600 г = 18% 500 х + 100 · 100 = 600 · 18 х = 8
Задача № 7 Сплавили два слитка серебра: 75 г 600 -й пробы и 150 г 864 -й пробы. Определить пробу сплава.
Сплавили два слитка серебра: 75 г 600 -й и 150 г 864 -й пробы. Определить пробу сплава. 75 г 600 150 г + 864 225 г = 75· 600 + 150 · 864 = 225 · х х = 776 х
Задача № 8 Смешали некоторое количество 15%-го раствора некоторого вещества с таким же количеством 19%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Смешали некоторое количество 15%-го раствора некоторого вещества с таким же количеством 19%го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? 15% + 19% = Х%
Смешали некоторое количество 15%-го раствора некоторого вещества с таким же количеством 19%го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? у 2 у 15% + 19% = 15 у + 19 у = 2 ух 15 + 19 = 2 х х = 17 Х%
Задача № 9 Имеется два сосуда. Первый содержит 100 кг, а второй 60 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Имеется два сосуда. Первый содержит 100 кг, а второй 60 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде? 100 кг Х% + 60 кг у% = 160 кг 19%
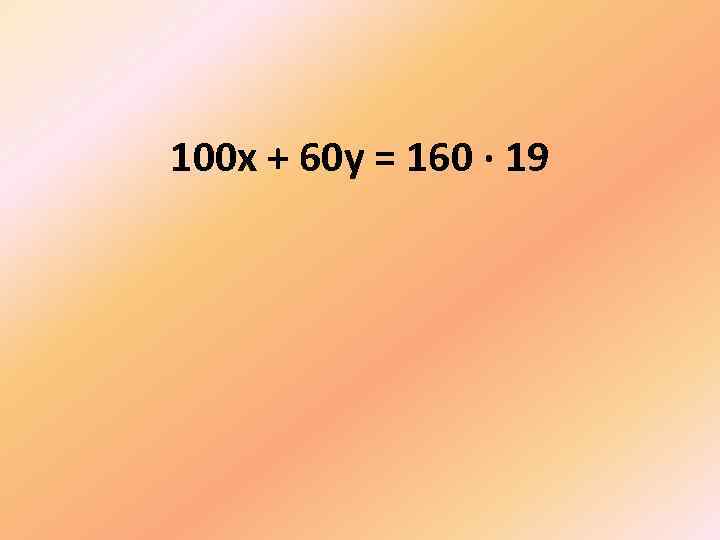100 х + 60 у = 160 · 19
Имеется два сосуда. Первый содержит 100 кг, а второй 60 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде? Х% + у% = 22%
Имеется два сосуда. Первый содержит 100 кг, а второй 60 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22 % кислоты. Сколько килограммов кислоты содержится в первом сосуде? р Х% + р 2 р у% = 22%
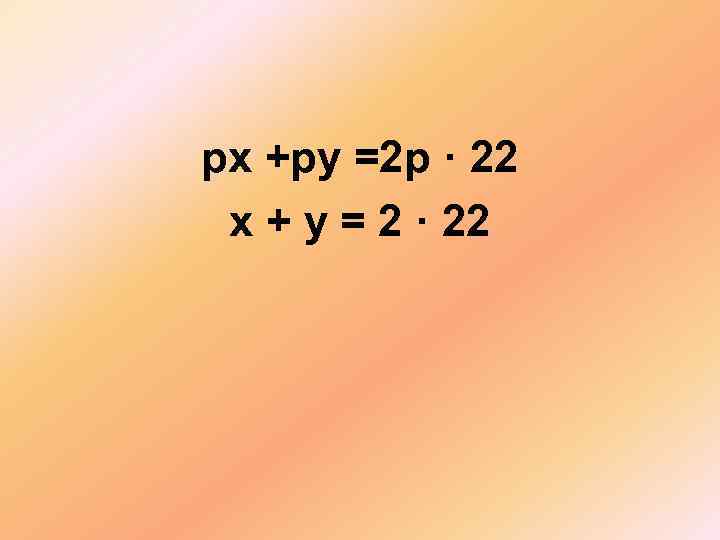рх +ру =2 р · 22 х + у = 2 · 22
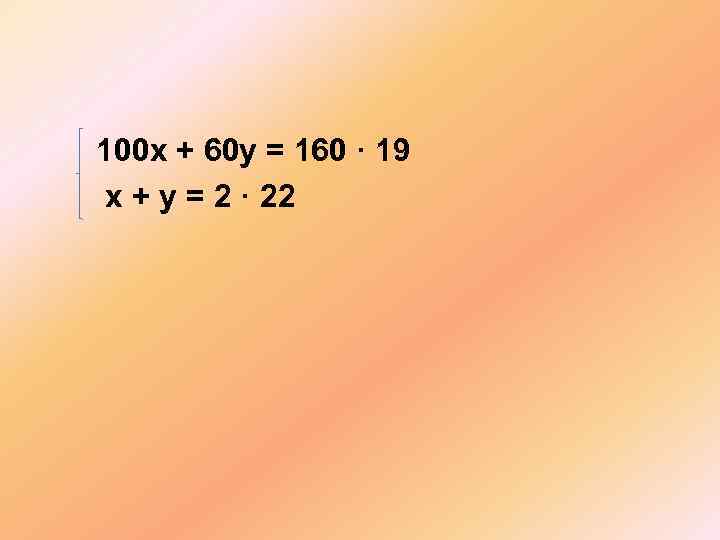100 х + 60 у = 160 · 19 х + у = 2 · 22
Задача № 10 Смешав 30%-ый и 60%-ый растворы кислоты и добавив 10 кг чистой воды, получили 36%-ый раствор кислоты. Если бы вместо 10 кг воды добавили бы 10 кг 50%-ого раствора той же кислоты, то получили бы 41%-ый раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси?
Смешав 30%-ый и 60%-ый растворы кислоты и добавив 10 кг чистой воды, получили 36%-ый раствор кислоты. Если бы вместо 10 кг воды добавили бы 10 кг 50%-ого раствора той же кислоты, то получили бы 41%-ый раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси? х кг у кг + 30% 60% (х+у+10) кг 10 кг + = 0% 36% 30 х +60 у +10 · 0 = 36(х + у +10)
Смешав 30%-ый и 60%-ый растворы кислоты и добавив 10 кг чистой воды, получили 36%-ый раствор кислоты. Если бы вместо 10 кг воды добавили бы 10 кг 50%-ого раствора той же кислоты, то получили бы 41%-ый раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси? х кг у кг + 30% 60% (х+у+10) кг 10 кг + = 50% 41% 30 х +60 у +10 · 50 = 36(х + у +10)
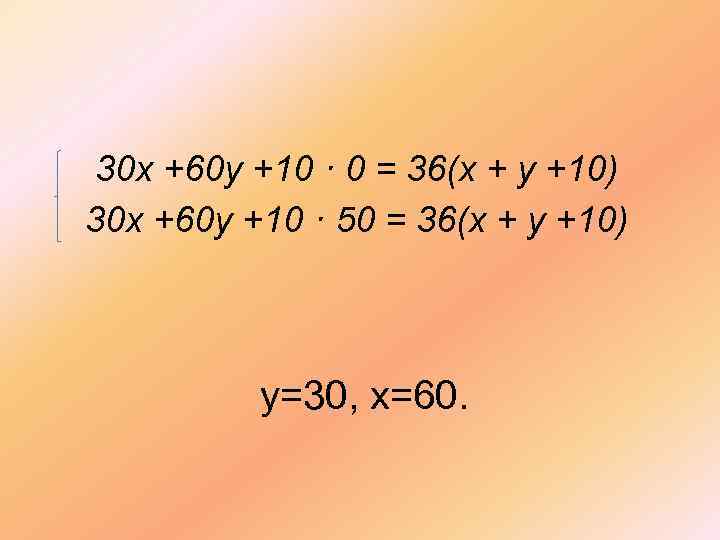30 х +60 у +10 · 0 = 36(х + у +10) 30 х +60 у +10 · 50 = 36(х + у +10) у=30, х=60.
Задача № 11 Влажность свежих грибов 90%, а сухих 15%. Сколько сухих грибов получится из 1, 7 кг свежих?
Влажность свежих грибов 90%, а сухих 15%. Сколько сухих грибов получится из 1, 7 кг свежих? свежие сухие 1, 7 кг х кг = 10% 1, 7 · 10 = х · 85, 85% х =0, 2
Задача № 12 Руда содержит 40% примесей, а выплавленный из нее металл содержит 4% примесей. Сколько тонн руды необходимо взять, чтобы выплавить из нее 15 тонн металла?
Руда содержит 40% примесей, а выплавленный из нее металл содержит 4% примесей. Сколько тонн руды необходимо взять, чтобы выплавить из нее 15 тонн металла? руда металл х т 15 т = 60% 60 · х = 15 · 96, 96% х =24
Задача № 13 Два сосуда со щелочью разных концентраций содержат вместе 20 литров раствора. Первый сосуд содержит 4 л щелочи, а второй – 6 л. Сколько процентов щелочи содержит первый сосуд, если второй содержит щелочи на 40% меньше первого?
Два сосуда со щелочью разных концентраций содержат вместе 20 литров раствора. Первый сосуд содержит 4 л щелочи, а второй – 6 л. Сколько процентов щелочи содержит первый сосуд, если второй содержит щелочи на 40% меньше первого? • 20 л 4 л 6 л
1) Имеется два сплава. Первый сплав содержит 10% никеля, второй – 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго? 2) Первый сплав содержит 5% меди, второй – 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. 4) Смешав 6 -процентный и 74 -процентный растворы кислоты и добавив 10 кг чистой воды, получили 19 -процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50 процентного раствора той же кислоты, то получили бы 24 процентный раствор кислоты. Сколько килограммов 6 процентного раствора использовали для получения смеси?
Источник
ПОДЕЛИТЬСЯ
Задания и ответы для Московской олимпиады школьников (МОШ) по физике 7,8,9,10,11 класс первого тура отборочного этапа 2020-2021 ученый год, официальная дата проведения олимпиады: 16.10.2020-18.10.2020 (с 16 по 18 октября 2020 года).
Ссылка для скачивания заданий для 7 класса: скачать в PDF
Ссылка для скачивания заданий для 8 класса: скачать в PDF
Ссылка для скачивания заданий для 9 класса: скачать в PDF
Ссылка для скачивания заданий для 10 класса: скачать в PDF
Ссылка для скачивания заданий для 11 класса: скачать в PDF
P.S свои ответы предлагайте ниже в комментариях, помогите друг другу.
Московская олимпиада школьников по физике 7 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Для определения скорости игрушечного поезда, который работает на батарейках, достаточно иметь… 1) Весы; 2) мензурку; 3) линейку; 4) часы; 5) микрометр; 6) ареометр.
2)Переведите в СИ: 150 000 мг (миллиграмм).
3)Цена деления мензурки, изображённой на рисунке, равна.
4)В мензурках находится вода. Какой объём воды будет в первой мензурке, если в неё перелить пятую часть воды из второй мензурки и половину воды из третьей мензурки?
5)Три шестёренки зацеплены зубьями между собой, как показано на рисунке, и могут вращаться вокруг закрепленных осей. Куда вращается нижняя («образование») шестеренка, если верхняя («успех») вращается по часовой стрелке?
Сколько оборотов в день делает нижняя шестерня («образование»), если известно, что верхняя («успех») делает 28 оборотов в неделю?
6)Из пункта А почтальон Печкин выехал на велосипеде в 12:00, направляясь в пункт Б. Одновременно с ним из пункта Б выехал на самокате дядя Фёдор, направляясь в пункт А. Впоследствии почтальон Печкин рассказывал, что в 12:30 встретил дядю Фёдора. Дядя Фёдор же вспоминал, что прибыл в пункт А в 13:15. Что показывали часы почтальона Печкина, когда он добрался до пункта Б? Считайте, что почтальон Печкин и дядя Фёдор двигались с постоянными скоростями. В качестве ответа запишите отдельно два числа – число часов (от 0 до 23) и целое число минут (от 0 до 59).
7)Дядя Вася хочет полностью наполнить две стоящие рядом бочки водой, не пролив её на землю. Он кладёт шланг в меньшую бочку, идёт к крану, открывает его и возвращается назад. После возвращения он ждёт 15 секунд, пока бочка заполнится, и перекладывает шланг в другую бочку. Подождав еще 2 минуты, дядя Вася возвращается к крану и закрывает его. Чему равно расстояние от бочек до крана, если дядя Вася ходит со скоростью 1 м/с, а вторая бочка по объёму вчетверо больше первой? Ответ выразите в м, округлите до целого числа.
8)Левая шкала измеряет объём жидкости в миллилитрах (ml), правая в – «чашках» (cup).
Чему равна цена деления левой шкалы? Ответ выразите в мл, округлите до целого числа.
Чему равна цена деления правой шкалы? Ответ выразите в «чашках», округлите до тысячных.
Найдите, чему равно расстояние между двумя ближайшими рисками на правой шкале, если на левой оно равно 1 см. Ответ выразите в мм, округлите до десятых.
Московская олимпиада школьников по физике 8 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Переведите в СИ: 321 л, 1 день
2)Таракан ползёт по прямой. Первые 10 с его скорость постоянна и равна 20 см/с, следующие 20 с его скорость составляет 16 см/с, затем он 10 с стоит на месте. Остаток пути он ползёт с постоянной скоростью 13 см/с. Найти среднюю скорость таракана на всем пути.
3)В каком случае перевозить камень на тачке удобнее?
4)К пружине, жёсткость которой k=100 Н/м, прикрепили грузик. Пружина удлинилась на Δx1=5 см. Если грузик погрузить в жидкость, удлинение пружины станет равным Δx2=2 см. Какая сила Архимеда действует на грузик в жидкости?
5)Однородные шарики покоятся на рычажных весах, как показано на рисунке. Плотность какого из шаров наименьшая? V2>V1=V3.
6)Кеша и Тучка, находясь в своих домиках, получили одновременно СМС-ки от Лисички с информацией, что яблочный пирог уже готов, и тут же бросились бежать к дому Лисички. Кеша половину времени бежал со скоростью 5 м/с, а оставшуюся половину времени со скоростью 4 м/с (устал). Тучка первую половину пути пробежал со скоростью 4 м/с, а вторую половину пути со скоростью 5 м/с. В результате оба прибежали к Лисичке одновременно. Каково расстояние от дома Кеши до дома Лисички в шагах Цыпы, если расстояние от дома Тучки до дома Лисички равно 800 шагов Цыпы?
7)Атос и Портос начинают одновременно идти навстречу друг другу со скоростями v1=3 м/с и v2=1 м/c соответственно. Арамис сначала находится посередине между ними. Портос встретился с Арамисом через t1=250 с после начала своего движения, а с Атосом через t2=12 мин.
На каком расстоянии друг от друга первоначально находились Атос и Портос? Ответ выразите в м, округлите до целого числа.
Насколько позже стартовал Арамис, если скорость сближения Портоса с Арамисом в 2 раза больше скорости удаления Арамиса от Атоса? Ответ выразите в с, округлите до целого числа.
8)На тарелке лежит торт, состоящий из трёх слоёв. Эти слои имеют высоту h1=15 мм, h2=25 мм и h3=20 мм, а их плотности соответственно равны ρ1=600 кг/м3, ρ2=460 кг/м3 и ρ3=400 кг/м3. Чему равна средняя плотность всего торта? Ответ выразите в кг/м3, округлите до целого числа.
9)В двух сообщающихся сосудах, имеющих форму цилиндров c площадью дна S1=100 см2 и S2=200 см2, находится вода. Сосуды закрыты сверху массивными поршнями (см. рисунок).
К правому поршню прикреплена легкая вертикальная пружина жёсткостью k=4 Н/см , верхний конец которой неподвижен. Система находится в равновесии, причём пружина изначально сжата. На левый поршень положили груз массой m=1 кг. Плотность воды ρ=1000 кг/м3, ускорение свободного падения g=10 Н/кг. Начальная высота края правого сосуда над поверхностью воды h=10 см.
Найдите, на сколько после этого опустится левый поршень. Ответ выразите в см, округлите до целого числа.
Груз какой минимальной массы нужно добавить к грузу массой m (на левый поршень) для того, чтобы вода начала выливаться из правого сосуда? Ответ выразите в кг, округлите до целого числа.
10)Система состоит из невесомых блоков, трёх грузов массой m=1 кг каждый, двух грузов массой mx каждый и невесомых нитей. Ускорение свободного падения g=10 Н/кг.
Чему равна величина mx, если система находится в равновесии? Ответ выразите в кг, округлите до десятых.
C какой силой действует система на потолок? Ответ выразите в Н, округлите до целого числа.
Московская олимпиада школьников по физике 9 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Улитка ползёт по прямой. Первый час её скорость постоянна и равна 1,2 см/с, еще два часа её скорость составляет 0,8 см/с, затем она ровно час отдыхала неподвижно. Остаток пути она ползла с постоянной скоростью 0,7 см/с. Найти среднюю скорость улитки на всем пути.
2)В сосуде с водой плавают два шара с радиусами 2R и R, как показано на рисунке. Чему равна плотность первого шара?
3)Система из двух блоков, двух грузов и обезьянки, находится в равновесии. Определите массу тела m1, если масса второго груза равна 2m, а масса обезьяны – m. Нити и блоки невесомые, трения нет.
4)В трёх кастрюлях находится вода. В первой кастрюле вода только закипела, во второй кипит 3 минуты, в третьей кипит 10 минут. В какой из кастрюль температура воды наибольшая?
5)Сто резисторов с сопротивлениями 1 Ом, 3 Ом, 5 Ом, … , 197 Ом, 199 Ом соединили параллельно. Эквивалентное сопротивление…
6)Рассмотрим объединение двух однополосных дорог A и B в однополосную дорогу C. В часы пик все три дороги заполнены автомобилями. Среднее расстояние между двумя соседними автомобилями можно считать одинаковым на всех трёх дорогах. Длина дороги A равна LA=1 км, дороги B: LB=3 км, а дороги C: LC=2 км. Средняя скорость автомобилей на дороге A составляет vA=3 км/ч, а среднее время, за которое машины проезжают дорогу B, равно tB=36 мин. За какое время в среднем автомобиль добирается от начала дороги A до конца дороги C? Ответ выразите в минутах, округлите до целого числа.
7)К невесомой системе, состоящей из нерастяжимых ниток, двух блоков и трёх пружин с коэффициентами жёсткости k и 2k, прикрепляют груз массой m=600 г, как показано на рисунке. k=50 Н/м, ускорение свободного падения равно 10 м/c2.
На какое расстояние опустится груз, когда система придёт в равновесие? Ответ выразите в см, округлите до десятых.
С какой силой система действует на потолок в положении равновесия? Ответ выразите в Н, округлите до целого числа.
8)Г-образный сосуд, наполненный ртутью и керосином, стоит на столе, как показано на рисунке. Силы давления жидкостей (без учета атмосферного давления) на горизонтальные стенки сосуда AB и CD, перпендикулярные плоскости рисунка, равны 40 Н и 8 Н соответственно. Известно, что при малейшем добавлении керосина в сосуд, он опрокидывается. Найдите отношение высоты столба ртути к высоте столба керосина. Ответ округлите до десятых. Плотность керосина 800 кг/м3, плотность ртути 13600 кг/м3.
9)Электрическая схема изменяет мощность W электрического нагревателя по линейному закону от времени t, прошедшего после включения нагревателя: W(t)=W0∙t/τ. W0=100 Вт, τ=10 секунд. Этот нагреватель помещён на дно банки с 1 литром воды в ней. Начальная температура воды 20°С. Пренебрегая теплоёмкостью банки и потерями теплоты в окружающую среду, найдите, какой стала температура воды в банке через 3 минуты после включения нагревателя? Удельная теплоёмкость воды 4,2 Дж/(г∙℃). Ответ выразите в градусах по шкале Цельсия, округлите до десятых.
10)Электрическая цепь состоит из идеальной батарейки с напряжением 3,2 В, резистора, идеального амперметра и двух вольтметров. Первый вольтметр показывает 1 В, а второй 2 В. Показание амперметра 1 мкА.
Чему равно сопротивление первого вольтметра? Ответ выразите в МОм, округлите до целого числа.
Чему равно сопротивление второго вольтметра? Ответ выразите в МОм, округлите до целого числа.
Чему равно сопротивление резистора? Ответ выразите в кОм, округлите до целого числа.
Московская олимпиада школьников по физике 10 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Тело движется вдоль оси ОХ. Какой физический смысл имеет площадь под графиком зависимости проекции ускорения тела от времени? Эта площадь пропорциональна
2)На графике зависимости массы планеты m от её радиуса R точки соответствуют разным планетам. На какой планете наибольшее ускорение свободного падения?
3)В каком случае на покоящееся тело массой m действует наименьшая сила взаимодействия с опорой?
4)Происходит абсолютно упругий центральный удар двух шаров. Известно, что m1<m2, v1>v2. Отношение модулей изменения импульса шариков в результате удара Δp1/Δp2:
5)Сто резисторов с сопротивлениями 1 Ом, 2 Ом, 3 Ом, … , 99 Ом, 100 Ом соединили параллельно. Эквивалентное сопротивление…
6)В спортивном зале мяч бросили вертикально вверх со скоростью 20 м/с (условно с поверхности пола). Определите время возврата мяча в начальную точку броска, если «высота потолка» равна 10 метрам. Ускорение свободного падения считайте равным 10 м/с2. Ответ выразите в секундах, округлите до сотых.
7)Полый шар, наполовину залитый воском, удерживается в равновесии вертикальной нитью и клином с углом при вершине α=30°, расположенным на горизонтальной поверхности.
Чему равно минимальное значение коэффициента трения μ между шаром и клином? Ответ округлите до сотых.
Чему равна по величине сила трения Fтр, действующая на клин со стороны плоскости? Ответ выразите в Н, округлите до целого числа.
8)Имеются три цилиндрических сообщающихся сосуда. «Средний» сосуд является посредником между «крайними» сосудами (первым и вторым). В первоначальном состоянии полным является первый сосуд (два крана закрыты). Открывают первый кран (заполняется сосуд «посредник»). Закрывается первый кран и открывается второй кран. Заполняется второй сосуд. Какова должна быть площадь сечения S сосуда «посредника», чтобы объем воды, поступивший во второй сосуд, был максимальным? Площадь сечения первого сосуда S1=16 см2, второго – S2=36 см2. Ответ выразите в см2, округлите до целого числа.
9)Взятые из холодильника стальные гвозди помещают в цилиндрический сосуд в воду с начальной температурой 0℃, в результате чего уровень воды в сосуде поднялся на 28,0 мм. После этого уровень воды медленно поднялся ещё на 0,6 мм. Какова была начальная температура гвоздей? Удельная теплоёмкость стали 500 Дж/(кг·К), удельная теплота плавления льда 340 кДж/кг, плотность воды 1000 кг/м3, плотность льда 900 кг/м3, плотность стали 7800 кг/м3. Ответ выразите в градусах по шкале Цельсия, округлите до целого числа.
10)Электрическая цепь состоит из идеальной батарейки с напряжением на выводах 7 В, идеальных приборов и пяти одинаковых резисторов с сопротивлением 100 Ом.
Что показывает амперметр? Ответ выразите в мА, округлите до целого числа.
Что показывает вольтметр? Ответ выразите в В, округлите до целого числа.
Московская олимпиада школьников по физике 11 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Происходит абсолютно упругий центральный удар двух шаров. Известно, что m1<m2, v1>v2. Отношение модулей изменения импульса шариков в результате удара Δp1/Δp2
2)В неподвижном лифте находится U-образная трубка с двумя жидкостями, плотности которых ρ1 и ρ2.
Как изменится разность уровней жидкостей в трубке Δh, если лифт начнёт двигаться ускоренно вверх?
3)В сосуде содержится смесь азота N2 и неона Ne. Сравните средние кинетические энергии поступательного движения молекул азота KN2 и неона KNe. Молярная масса азота N2 больше, чем молярная масса неона Ne.
4)Над газом постоянного состава и количества осуществили процесс 1−2−3−4−5. На каком участке внутренняя энергия газа уменьшалась?
5)Какой физической величине соответствует выражение qat/l, где: q -заряд, a – ускорение, l – длина, t – время?
6)Какого максимального значения достигает в процессе полёта угловая скорость вращения вектора скорости тела, брошенного с начальной скоростью 10 м/с под углом 60°? Ускорение свободного падения равно 10 м/c2 . Ответ выразите в рад/c, округлите до целого числа.
7)Металлическое ведро в форме усечённого конуса имеет высоту h=25 см и объём (вместимость) V=12 л. Пустое ведро имеет массу m0=1 кг. Ведро полностью заполнили водой, соединили невесомым нерастяжимым тросом, перекинутым через блок, с грузом массой M=5 кг, и отпустили. Ведро и груз пришли в движение. С какой силой вода давит на дно ведра при движении этой системы? Дно ведра – круг радиусом r=10 см. Атмосферное давление не учитывать. Трением, сопротивлением воздуха и массой блока пренебречь. Плотность воды ρ=1000 кг/м3, ускорение свободного падения g=10 м/с2. Ответ выразите в Н, округлите до десятых.
8)Дирижабль, наполненный водородом, находится в сухом воздухе, температура которого равна 20℃ и давление 95,3 кПа. Объём дирижабля равен 31900 м3. Молярная масса воздуха равна 29 г/моль, универсальная газовая постоянная равна R=8,31 Дж/(моль∙К). Плотность насыщенного водяного пара при температуре 20℃ равна 0,017 кг/м3 . Какова подъёмная сила, действующая на дирижабль со стороны воздуха? Ответ выразите в кН, округлите до целого числа.
Чему была бы равна подъёмная сила при относительной влажности 70%, той же температуре и давлении? Ответ выразите в кН, округлите д