В геометрическом сосуде объемом

Êëèêíèòå, ÷òîáû äîáàâèòü â èçáðàííûå ñåðâèñû.
Êëèêíèòå, ÷òîáû óäàëèòü èç èçáðàííûõ ñåðâèñîâ.
Ôîðìóëà îáúåìà êóáà, øàðà, ïèðàìèäû, ïàðàëëåëîãðàììà, öèëèíäðà, òåòðàýäðà, êîíóñà, ïðèçìû è îáúåìû äðóãèõ ãåîìåòðè÷åñêèõ ôèãóð.
Ôîðìóëà îáúåìà íåîáõîäèìà äëÿ âû÷èñëåíèÿ ïàðàìåòðîâ è õàðàêòåðèñòèê ãåîìåòðè÷åñêîé ôèãóðû.
Îáúåì ôèãóðû – ýòî êîëè÷åñòâåííàÿ õàðàêòåðèñòèêà ïðîñòðàíñòâà, çàíèìàåìîãî òåëîì èëè âåùåñòâîì.  ïðîñòåéøèõ ñëó÷àÿõ îáú¸ì èçìåðÿåòñÿ ÷èñëîì óìåùàþùèõñÿ â òåëå åäèíè÷íûõ êóáîâ, ò. å. êóáîâ ñ ðåáðîì, ðàâíûì åäèíèöå äëèíû. Îáú¸ì òåëà èëè âìåñòèìîñòü ñîñóäà îïðåäåëÿåòñÿ åãî ôîðìîé è ëèíåéíûìè ðàçìåðàìè.
| Ôèãóðà | Ôîðìóëà | ×åðòåæ |
|---|---|---|
Ïàðàëëåëåïèïåä. Îáúåì ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà ðàâåí ïðîèçâåäåíèþ ïëîùàäè îñíîâàíèÿ íà âûñîòó. | V= SH= abh |
|
Öèëèíäð. Îáúåì öèëèíäðà ðàâåí ïðîèçâåäåíèþ ïëîùàäè îñíîâàíèÿ íà âûñîòó. Îáúåì öèëèíäðà ðàâåí ïðîèçâåäåíèþ ÷èñëà ïè (3.1415) íà êâàäðàò ðàäèóñà îñíîâàíèÿ íà âûñîòó. | V = Sh, V = πr2h |
|
Ïèðàìèäà. Îáúåì ïèðàìèäû ðàâåí îäíîé òðåòè ïðîèçâåäåíèÿ ïëîùàäè îñíîâàíèÿ S (ABCDE) íà âûñîòó h (OS). | V = 1/3*Sh |
|
Ïðàâèëüíàÿ ïèðàìèäà — ýòî ïèðàìèäà, â îñíîâàíèè, êîòîðîé ëåæèò ïðàâèëüíûé ìíîãîóãîëüíèê, à âûñîòà ïðîõîäèò ÷åðåç öåíòð âïèñàííîé îêðóæíîñòè â îñíîâàíèå. |
|
|
Ïðàâèëüíàÿ òðåóãîëüíàÿ ïèðàìèäà — ýòî ïèðàìèäà, ó êîòîðîé îñíîâàíèåì ÿâëÿåòñÿ ðàâíîñòîðîííèé òðåóãîëüíèê è ãðàíè ðàâíûå ðàâíîáåäðåííûå òðåóãîëüíèêè. | V = ha2/4√3 |
|
Ïðàâèëüíàÿ ÷åòûðåõóãîëüíàÿ ïèðàìèäà — ýòî ïèðàìèäà, ó êîòîðîé îñíîâàíèåì ÿâëÿåòñÿ êâàäðàò è ãðàíè ðàâíûå ðàâíîáåäðåííûå òðåóãîëüíèêè. | V = 1/3*ha2 | |
Òåòðàýäð — ýòî ïèðàìèäà, ó êîòîðîé âñå ãðàíè — ðàâíîñòîðîííèå òðåóãîëüíèêè. | V = (a3√2)/12 |
|
Óñå÷åííàÿ ïèðàìèäà. Îáúåì óñå÷åííîé ïèðàìèäû ðàâåí îäíîé òðåòè ïðîèçâåäåíèÿ âûñîòû h (OS) íà ñóììó ïëîùàäåé âåðõíåãî îñíîâàíèÿ S1(abcde), íèæíåãî îñíîâàíèÿ óñå÷åííîé ïèðàìèäû S2 (ABCDE) è ñðåäíåé ïðîïîðöèîíàëüíîé ìåæäó íèìè. | V= 1/3 h (S1+ √S1S2 + S2) |
|
Êóá. Âû÷èñëèòü îáúåì êóáà ëåãêî – íóæíî ïåðåìíîæèòü äëèíó, øèðèíó è âûñîòó. Òàê êàê ó êóáà äëèíà ðàâíà øèðèíå è ðàâíà âûñîòå, òî îáúåì êóáà ðàâåí s3. | V = s3 |
|
Êîíóñ — ýòî òåëî â åâêëèäîâîì ïðîñòðàíñòâå, ïîëó÷åííîå îáúåäèíåíèåì âñåõ ëó÷åé, èñõîäÿùèõ èç îäíîé òî÷êè (âåðøèíû êîíóñà) è ïðîõîäÿùèõ ÷åðåç ïëîñêóþ ïîâåðõíîñòü. | V = 1/3 πR2H |
|
Óñå÷åííûé êîíóñ ïîëó÷èòñÿ, åñëè â êîíóñå ïðîâåñòè ñå÷åíèå, ïàðàëëåëüíîå îñíîâàíèþ. | V = 1/3 πh (R2 + Rr + r2) |
|
Øàð. Îáúåì øàðà â ïîëòîðà ðàçà ìåíüøå, ÷åì îáúåì îïèñàííîãî âîêðóã íåãî öèëèíäðà. | V = 4/3 πr3 |
|
Ïðèçìà. Îáúåì ïðèçìû ðàâåí ïðîèçâåäåíèþ ïëîùàäè îñíîâàíèÿ ïðèçìû, íà âûñîòó. | V = So h |
|
Ñåêòîð øàðà. Îáúåì øàðîâîãî ñåêòîðà ðàâåí îáúåìó ïèðàìèäû, îñíîâàíèå êîòîðîé èìååò òó æå ïëîùàäü, ÷òî è âûðåçàåìàÿ ñåêòîðîì ÷àñòü øàðîâîé ïîâåðõíîñòè, à âûñîòà ðàâíà ðàäèóñó øàðà. | V = 1/3 R S = 2/3 π R2 h |
|
Øàðîâîé ñëîé — ýòî ÷àñòü øàðà, çàêëþ÷åííàÿ ìåæäó äâóìÿ ñåêóùèìè ïàðàëëåëüíûìè ïëîñêîñòÿìè. | V = 1/6 π h3 + 1/2 π (r12+ r22) h |
|
Ñåãìåíò øàðà – ýòî ÷àñòü øàðà, îñåêàåìàÿ îò íåãî êàêîé-íèáóäü ïëîñêîñòüþ, íàçûâàåòñÿ øàðîâûì èëè ñôåðè÷åñêèì ñåãìåíòîì | V = π h2 ( R – 1/3 h) |  |
Äîïîëíèòåëüíûå ìàòåðèàëû ïî òåìå: Ôîðìóëà îáúåìà.
| |||||||||||||
| |||||||||||||
|
| ||||||||||||
Источник
1. Расчет объема куба

a – сторона куба
Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
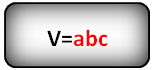
3. Формула для вычисления объема шара, сферы

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

4. Как вычислить объем цилиндра ?
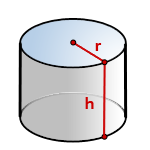
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

5. Как найти объем конуса ?
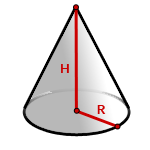
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
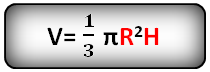
7. Формула объема усеченного конуса
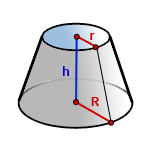
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

8. Объем правильного тетраэдра
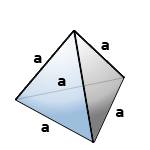
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
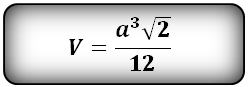
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
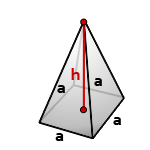
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
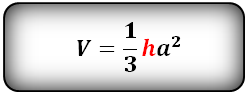
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
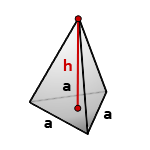
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
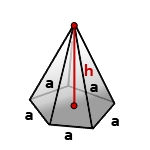
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
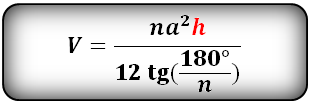
12. Расчет объема пирамиды
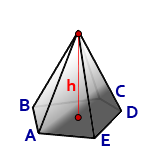
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
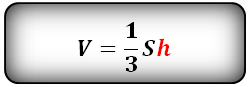
13. Расчёт объёма усечённой пирамиды
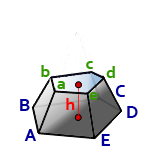
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

14. Объем шарового сегмента, формула
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
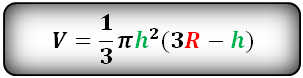
15. Объем шарового сектора
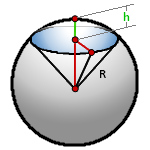
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

16. Объем шарового слоя
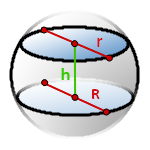
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
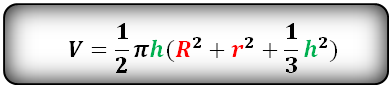
Источник
При работе со своими учениками, у меня накапливается много задач. Поэтому я публикую разборы задач в свободный доступ, стараюсь делать это максимально подробно и понятно, чтобы начинающие могли прочитать и разобраться в нужной для них теме. Ну а за подробными индивидуальными консультациями и репетиторством вы можете написать в мою группу в вк или в личные сообщения. Также большое количество разборов задач вы сможете найти в моей группе Репетитор IT mentor
Задача 1. На тело массой 100 кг, лежащее на наклонной плоскости, которая образует с горизонтом угол 40°, действует горизонтальная сила 1500 Н. Определить:
1) силу, прижимающую тело к плоскости;
2) силу трения тела о плоскость;
3) ускорение, с которым поднимается тело. Коэффициент трения k = 0.10; g = 10м/с².
Задача 2. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Найти ускорение тела, если на него действует сила тяжести P, а коэффициент трения между телом и плоскостью равен k . При какой величине силы F движение будет равномерным.
Задача 3. Два шара массами m1 = 2.5 кг и m2 = 1.5 кг движутся навстречу друг другу со скоростями v1 = 6 м/c и v2 = 2 м/c . Определить: 1) скорости шаров после удара; 2) кинетические энергии шаров до и после удара; 3)энергию, затраченную на деформацию шаров при ударе. Удар считать прямым, неупругим.
Прикрепляю очередной разбор задачи по физике по теме закона сохранения импульса. Неупругие шары после удара не восстанавливают свою первоначальную форму. Таким образом, сил, которые отталкивали бы шары друг от друга, не возникает. Это значит, что после удара шары будут двигаться вместе (слипшись) с одной и той же скоростью . Эту скорость определим по закону сохранения импульса. Так как шары двигаются по одной прямой, то можно записать импульс системы до удара и после удара. Считаем, что в задаче не действует диссипативных сил (сил трения, сопротивления воздуха и т.д.), поэтому импульс вдоль оси Ox сохраняется, тогда (смотри решение на картинке). Расписал довольно подробно, но если что-то не будет понятно, то задавайте вопросы в комментариях.
Задача 4. Диск массой m, радиус которого R , вращается с угловой скоростью ω0 вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. После прекращения действия на него силы диск останавливается в течение времени t. Определить угловое ускорение диска и тормозящий момент, действующий на него.
Задача 5. Два тела массами m1 и m2 связаны нитью, перекинутой через блок массой M . Найти ускорение тел, считая блок сплошным диском.
Задача 6. Шар катится по горизонтальной поверхности со скоростью v . На какую высоту h относительно своего первоначального положения поднимется шар, если он начнет вкатываться на наклонную плоскость без проскальзывания?
Задача 7. На краю вращающейся с угловой скоростью ω0 платформе стоит человек массой m. После того, как человек перешёл в другую точку платформы, угловая скорость её вращения стала равной ω. Найти расстояние от оси вращения до человека, считая платформу диском массой M и радиусом R.
Задача 8. Тело массой m брошено со скоростью v0 под углом α к горизонту. Найти кинетическую и потенциальную энергию тела в высшей точке траектории.
Задача 9. На горизонтальной поверхности находятся два тела массами m1 = 10 кг и m2 =15 кг, связанные нитью. К телу массой m2 прикладывают силу F = 100 Н, направленную под углом α = 60° к горизонту. Определить ускорение грузов и силу натяжения нити, соединяющей грузы. Трением пренебречь. (обязательно указать все силы на чертеже!)
Задача 10. На поверхности стола лежит груз массой m2 = 2 кг. На нити, прикрепленной к грузу m2 и перекинутой через невесомый блок, подвешен груз m1 = 1 кг. Коэффициент трения груза о поверхность стола 0,2. Найти ускорение грузов и силу натяжения нити.
Задача 11. Лодка массой 200 кг и длиной 3 м стоит неподвижно в стоячей воде. Мальчик массой 40 кг в лодке переходит с носа на корму. Определите, на какое расстояние при этом сдвинется лодка.
Считаем, что в нашей задаче не действует внешних сил, поэтому по теореме о центре массы системы грузов, можно считать, что координаты центра масс сохраняются в проекциях на ось OX (по оси OY движения не происходит). Проведем ось Y(ноль оси X) через центр лодки, тогда можно записать координаты человека и лодки до перехода человека с носа на корму.
Задача 12. Шарик массой 5 кг подвешен на нити. Нить может выдержать максимальное натяжение 100 Н. На какой минимальный угол от положения равновесия нужно отклонить нить с шариком, чтобы он оборвал нить, проходя через положение равновесия? (обязательно сделать рисунок, указать действующие силы!)
Задача 13. Два неупругих шара массами m1=2 кг и m2=3 кг движутся со скоростями соответственно v1=8 м/c и v2=4м/с. Определить количество теплоты, выделившееся при их столкновении. Рассмотреть 2 случая: 1) шары движутся навстречу друг другу; 2) меньший шар догоняет больший.
Задача 14. Тело совершает гармонические колебания по закону x(t) = 50⋅sin(π/3⋅t) (см). Определить полную энергию тела, если его масса 0,2 кг. Какая сила действует на тело в момент времени t = 0,5 с?
Задача 15. Два математических маятника, длины которых отличаются на Δℓ =16 см, совершают за одно и то же время: один − 10 колебаний, другой − 6 колебаний. Определить длины маятников.
Задача 16. Определить, сколько молей и молекул водорода содержится в объёме V = 5 м³ под давлением Р = 767 мм.рт.ст. при температуре t = 18 ° С. Какова плотность газа?
Задача 17. Сколько кислорода выпустили из баллона ёмкостью 1 дм3, если давление его изменилось от 14 атм до 7 атм, а температура от 27°С до 7 °С ?
Задача 18. В сосуде объёмом V = 2 м³ находится смесь m1 = 4 кг гелия и m2 = 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
Задача 19. В сосуде содержится смесь газов: гелия массой 12 г и водорода массой 2 г, температура в сосуде 77°С, давление 20 кПа. Определить молярную массу и плотность смеси газов.
Задача 20. Гелий массой 20 г нагрели от 100°С до 400°С, причем газу была передана теплота 30 кДж. Найти изменение внутренней энергии гелия и совершенную им работу.
Задача 21. При изотермическом расширении от 0,1 м3 трех молей газа его давление меняется от 4,48 атм до 1 атм. Найти совершаемую при этом работу и температуру, при которой протекает процесс.
Задача 22. Моль идеального газа, имевший первоначально температуру 300ºК, расширяется изобарически до тех пор, пока его объем не возрастет в 3 раза. Затем газ охлаждается изохорически до первоначальной температуры. Определить суммарное получаемое газом количество теплоты. Обязательно нарисовать графики процессов.
Задача 23. Азот массой m = 1 кг занимает при температуре Т1 = 300 К объём V = 0,5 м³. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определить конечный объём газа и конечную температуру.
Задача 24. Газ расширяется адиабатически, причём объём его увеличивается вдвое, а термодинамическая температура падает в 1,32 раза. Какое число степеней свободы i имеют молекулы этого газа?
Задача 25. Баллон ёмкостью V = 20 л с кислородом при давлении Р = 107 Па и температуре t1 = 70 ºС нагревается до температуры t2 = 270 ºС. Какое количество теплоты при этом поглощает газ?
Задача 26. Азот, занимающий при давлении, равном Р1 = 10⁵ Па объём V1 = 10 л, расширяется вдвое. Найти конечное давление и работу, совершённую газом в процессах: а) изобарном; б) изотермическом; в) адиабатном.
Задача 27. Кислород, масса которого 200 г, нагревают от температуры Т1 =300 К до Т2 = 400 К. Найти изменение энтропии, если известно, что начальное и конечное давление газа одинаковы и близки к атмосферному.
Задача 28. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 1,5∙10⁵ Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 260 К. Найти КПД машины, количество теплоты Q1, получаемое машиной за один цикл от нагревателя, и количество теплоты Q2, отдаваемое за один цикл холодильнику.
Задача 29. Найти суммарную кинетическую энергию Е поступательного движения всех молекул, содержащихся в объёме V = 1 дм³ газа при атмосферном давлении.
Задача 30. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 100 г водорода при температуре 400 К ? Чему равна полная внутренняя энергия газа?
Спасибо, что дочитали до конца, дорогие подписчики 🙂 Если вам интересен подобный контент и разборы задач, то оставляйте обратную связь в виде лайков и комментариев.
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в Telegram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Источник















