В герметически закрытом сосуде находится 5 моль

Ответом к каждому заданию В1–В4 и С1-С6 будет некоторое число, если необходимо, округлите его до одной значащей цифры после запятой. Это число надо внести в поле ответов. Каждый символ (цифру, запятую, знак минус) пишите без пробелов. Запятые в десятичных дробях вводятся обязательно точкой, например, 1.25. Единицы физических величин писать не нужно.

Желаем успеха!

B1. По преданию, царь Гиерон обратился к великому Архимеду с просьбой проверить, сплошная ли золотая корона, отлитая для него мастерами, или внутри имеется полость. Выполнив необходимые измерения и расчеты, ученый обнаружил, что внутри короны имеется пустота объемом 9 см3. Для этого Архимед взвесил корону в воздухе и в воде. В воде корона весила 9,22 Н (единица силы «ньютон» была введена значительно позже). Выполнив расчеты Архимеда, определите, сколько весила корона в воздухе. Плотность золота 19,3•103 кг/м3, плотность воды 1•103 кг/м3.

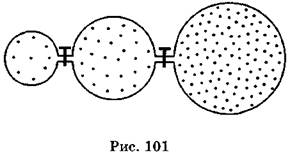
рис.101

B2. Три сферы радиусами 4 см, 8 см и 10 см заполнены газом и соединены тонкими трубками, перекрытыми кранами (рис. 101). Давление газа в левой сфере 0,2 МПа, давление газа в средней сфере 0,4 МПа, давление газа в правой сфере 0,8 МПа. Каким станет давление газа, если оба крана открыть?

B3. В 3 л воды при 40 °С бросили 50 г льда при -4 °С. Какая установилась температура после того, как весь лед растаял? Удельная теплоемкость воды 4,2•103 Дж/(кгК), удельная теплоемкость льда 2,1•103Дж/(кгК), удельная теплота плавления льда 3,3•105Дж/кг.

B4. В герметически закрытом сосуде находятся 5 моль идеального одноатомного газа при 270 С. Какое количество теплоты надо передать этому газу, чтобы его давление увеличилось в 3 раза?.

C1. Деревянный кубик с длиной ребра 5 см опускают в воду, а поверх наливают слой керосина вровень с верхней гранью кубика. Найти объем погруженной в воду части кубика. Плотность дерева 960 кг/м3, плотность керосина 800 кг/м3, плотность воды 1000 кг/м3.

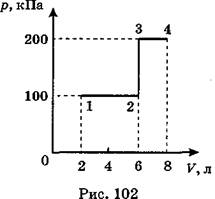
рис.102

C2. В идеальном газе происходит процесс, изображенный на рис. 102. Какое количество теплоты подведено к газу на протяжении всего процесса, начиная от состояния 1 и кончая состоянием 4?

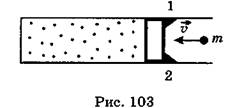
рис.103

C3. Идеальный одноатомный газ, находящийся в теплоизолированном сосуде объемом V под давлением р, заперт поршнем массой М (рис. 103). Справа поршень удерживают упоры 1 и 2, не давая газу расширяться. В поршень попадает пуля массой m, летящая горизонтально со скоростью v, и застревает в нем. Считая, что всю механическую энергию поршень передаст газу, определить, во сколько раз повысится температура газа. Процесс в газе изобарный.
Вычислите результат для V = 10 л, p = 105 Па, M = 90 г, m = 10 г, v = 1000 м/с.

C4. В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h. Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно. Вычислите это значение x при h = 10 см.

C5. Агрегат мощностью 50 кВт охлаждается проточной водой, текущей со скоростью 4 м/с по охватывающей агрегат трубке радиусом 5 мм. Начальная температура воды 10 °С. До какой температуры нагревается вода, если половина тепловой мощности агрегата идет на ее нагревание? Удельная теплоемкость воды 4200 Дж/(кгК).

C6. Тепловой двигатель совершает круговой цикл, соответствующий графику на рис. 104. Цикл состоит из двух изохор 1-2 и 3-4, и двух адиабат 2-3 и 4-1. Найти КПД этого цикла.

Источник

В герметически закрытом сосуде находится 5 моль

Физика для старшеклассников и абитуриентов

Дано:

t = 15 oC

m 100% = 40% m

‘T = 8 К

p1 — ? p2

Решение

Поскольку здесь речь идет о массе газа, воспользуемся уравнением Менделеева — Клапейрона, в которое эта масса входит. Запишем это уравнение для первого состояния, когда в баллоне была вся масса газа:

p1V = m RT . M

После того как из баллона вышла масса газа ‘m, в нем осталась масса m – ‘m, и при этом температура газа понизилась на ‘Т, т.е. стала равной Т – ‘Т. Поэтому теперь запишем уравнение Менделеева — Клапейрона для нового состояния:

p2V =

m − m

(T − T).

Теперь, чтобы найти отношение

, надо разделить первое

уравнение на второе и выполнить сокращения:

p1V

mRTM

p2V

M (m − m)R (T − T)

(m − m)(T − T)

Но нам не даны ни масса газа m, ни ее изменение ‘m, а дано

отношение

m,выраженноевпроцентах.Если m 100%=40%,

то m = 0,4. Чтобы получить отношение

m в последнем урав-

нении, разделим в его правой части числитель и знаменатель на m (от этого равенство не нарушится):

= m

−

(T − T)

−

(T − T)

Теперь заменим отношение						m его числовым значением
m	:	m

m
	p1	=	T	=	Ò

p2	(1 − 0, 4)(Ò −		Ò)		0,6 (Ò − Ò)

270

В герметически закрытом сосуде находится 5 моль

Раздел II. Молекулярная физика и термодинамика

Выразим начальную температуру в единицах СИ:

15 0С = 288 К.

Произведем вычисления:

ð1	=	288	= 1,7.
ð2	=	0,6 (288	= 1,7.	− 8)

Ответ: р1/р2 = 1,7.

В11. В баллоне с газом имелась щель, через которую газ просачивался. При нагревании этого газа его температура повысилась в 3 раза, а давление увеличилось в 1,5 раза. Во сколько раз изменилась масса газа в баллоне?

Обозначим m1 массу газа в баллоне до утечки газа, m2 — массугазавбаллонепослеутечки,р1 —начальноедавление, р2 — конечное давление, Т1 — начальную температуру, Т2 — конечную температуру, M — молярную массу газа, R — молярную газовую постоянную.

Дано:

Т2 = 3Т1

р2 = 1,5р1

m1 — ? m2

Решение

Воспользуемся уравнением Менделеева — Клапейрона с учетом, что объем баллона и газа в нем не менялся. Запишем это уравнение для первого и второго состояний газа:

р	V =	m1	RT и р		V =	m2	RT	.

1	M	1	2	M	2

Теперь разделим эти равенства друг на друга:

p1V

m1RT1M

m1T1

p2V Mm2RT2

m2T2

откуда

p1T2

p13Ò1

= 2.

p2T1

1,5ð1 Ò1

Ответ: масса газа уменьшилась в 2 раза.

В12. Ампула объемом 1 см3 содержит воздух при нормальных условиях. Ампула оставлена в космосе, в ней пробито отверстие. Через сколько времени давление в ампуле станет равно 0, если из нее каждую секунду вылетает 100 миллионов молекул?

271

В герметически закрытом сосуде находится 5 моль

Физика для старшеклассников и абитуриентов

Обозначим V объем ампулы, p — нормальное атмосферное давление, Т— абсолютную температуру в ампуле, N1 — число молекул, покидающих ампулу за время t1, k — постоянную Больцмана,t —время,закотороеампулупокинутвсемолекулы и давление в ней станет равно 0, N — все число молекул N, имевшихся в ампуле при нормальных условиях, n — концентрацию молекул в ампуле при нормальных условиях (105 Па и 273 К), V — объем ампулы.

Дано:			Решение
V = 1 см3			Время t, за которое ампулу покинут
p = 105 Па			все молекулы, можно найти, разделив все
Т = 273 К			число молекул N, имевшихся в ампуле
N1 = 108			при нормальных условиях, на число мо-
k		= 1,38 10−23 Äæ	лекул N1, покидающих ампулу за t1 = 1 c:
t	Ê	t =	N	t .
	= 1 с

1	N 1
1

t — ?

Таким образом, задача сводится к определению числа молекул N, содержавшихся в ампуле при нормальных условиях. Это число можно определить, умножив концентрацию молекул при этих условиях n на объем ампулы:

N = nV.

Нам не известна концентрация молекул газа n. Но ее мы легко определим из формулы, устанавливающей связь давления газа с его концентрацией и температурой,

p = knT.

Отсюда	p
n =		.

kT
Тогда	pV	.
N =

kT

Подставив полученное выражение в формулу для определения времени t, будем иметь

t = pVt1 . kTN1

Мы решили в общем виде эту задачу. Переведем все единицы в СИ: 1 см3 = 10–6 м3.

272

Раздел II. Молекулярная физика и термодинамика

Подставим числа и произведем вычисления:

t	105 10−6 1	11
	c ≈ 2,7 10 ñ.
		1,38 10−23 273 108

Ответ:t | 2,7 1011 c.

В13. В аудитории объемом 90 м3 температура воздуха повысилась с 20 0С до 30 0С. Атмосферное давление 105 Па, молярная масса воздуха 0,029 кг/моль, Какая масса воздуха вышла из комнаты?

Обозначим V объем воздуха в комнате, t1 — начальную температуру воздуха по шкале Цельсия, t2 — конечную температуру воздуха по шкале Цельсия, p — давление воздуха, M — молярную массу воздуха, ‘m — массу вышедшего из комнаты воздуха, R — молярную газовую постоянную, T1 — начальную абсолютную температуру, T2 — конечную абсолютную температуру, m1 — начальную массу воздуха в комнате, m2 — конечную массу воздуха в комнате.

Дано:	Решение

V = 90 м3	Запишем уравнение Менделее-
t1 = 20 0С	ва — Клапейрона применительно
t2 = 30 0С	к первому и второму состояниям
р = 105 Па	воздуха в комнате:
М = 0,029 кг/моль	р1V =	m1		RT1 и			р2V =	m2	RT2.
R = 8,31 Дж/(моль · К)
			M
M
Из этих уравнений найдем мас-
									‘m — ?
сы воздуха в первом и втором со-

стояниях:
m	=	pVM			и m	=		pVM	.
				2
1	RT1		RT2

Масса воздуха, вышедшего из комнаты, равна разности его масс в первом и втором состояниях:

‘m = m1	– m2	pVM	pVM	pVM	1	−	1
		=	–	=	.
							RT1	RT2	R	T2
T1

Задача в общем виде решена. Выразим все величины в единицах СИ: 20 0С = 293 К, 30 0С = 303 К.

273

В герметически закрытом сосуде находится 5 моль

Физика для старшеклассников и абитуриентов

Произведем вычисления:

105	90 0,029	1	−	1
‘m =		кг = 3,1 кг.
				8,31	303
293

Ответ: ‘m = 3,1 кг.

В14. При переходе определенной массы газа из одного состояния в другое его давление уменьшается, а температура увеличивается. Как при этом меняется его объем?

Обозначим р1, V1 и Т1 первоначальные давление, объем и температуру газа, а р2, V2 и Т2 — его конечные давление, объем и температуру.

Будем рассуждать так. Здесь меняются все параметры состояния данной массы газа: и его давление, и объем, и температура. Значит, чтобы ответить на вопрос задачи, воспользуемся уравнением Клапейрона (его еще называют объединенным газовым законом):

p1V1 = p2V2 . T1 T2

Согласно условию задачи давление газа уменьшается, а

температура увеличивается, значит, отношение			p2	меньше
			T
p1
	2
	отношения	, ведь в числителе справа от равенства давление
T

1

меньше, а температура в знаменателе больше, чем слева. Но тогда, чтобы само равенство сохранилось, конечный объем V2 в числителе правой части должен быть больше начального объема V1 (в противном случае, если и конечный объем будет

меньше начального, все выражение p2V2 , стоящее справа от

равенства будет меньше выражения p1V1 , стоящего слева, и

равенство нарушится). Значит, объем газа увеличивается. Ответ: объем увеличивается.

В15. В 3 л воды при 40 0С бросили 50 г льда при –4 0С. Какая установилась температура после того, как весь лед растаял? Удельная теплоемкость воды 4,2 · 103 Дж/(кг · К), удельная теплоемкость льда 2,1 · 103 Дж/)кг · К), удельная теплота плавления льда 3,3 · 105 Дж/кг.

274

В герметически закрытом сосуде находится 5 моль

Дано:

m1 = 3 кг t1 = 40 0C m2 = 50 г t2 = –4 0C

c1 = 4,2 · 103 Дж/(кг · К) с2 = 2,1 · 103 Дж/(кг · К) O = 3,3 · 105 Дж/кг

t0 = 0 0C

t — ?

Раздел II. Молекулярная физика и термодинамика

Обозначим m1 массу воды, в которую бросили лед, t1 — начальную температуру воды, m2 — массу льда, t2 — начальную температуру льда, c1 — удельную теплоемкость воды, c2 — удельную теплоемкость льда, O— удельную теплоту плавления льда, t0 — температуру плавления льда, t — установившуюся температуру, Q1 — количество теплоты, которое отдает горячая вода, остывая от температуры t1 до t, Q2 — количество теплоты , полученное льдом при нагревании от t2 до t0 = 0 0C, Q3 — количество теплоты, полученное льдом при плавлении, Q4 — количество теплоты, полученное водой, образовавшейся из растаявшего льда при нагревании от t0 = 0 0С до искомой температуры t.

Решение

Следует знать, что 1 л воды имеет массу 1 кг, поэтому мы вместо объема 3 л записали массу воды 3 кг, ведь в формулах количеств теплоты везде стоит масса.

Для решения этой задачи воспользуемся законом сохранения тепловой энергии, ведь здесь не идет речь о КПД процесса, и значит, сумма всех отданных ко-

личеств теплоты одними телами равна сумме всех количеств теплоты, полученных другими. В нашей задаче отдает количество теплоты Q1 только горячая вода, остывая от температуры t1 до t, поэтому

Q1 = c1m1(t1 – t) .

Получает эту теплоту лед. Поскольку он был при отрицательной температуре, то сначала он нагревается от t2 = –4 0С до t0 = 0 0С (выше 0 0С лед нагреть нельзя, он при этой температуре тает). Поэтому количество теплоты, полученное льдом при нагревании,

Q2 = c2m2(t0 – t2).

Поскольку тепло продолжает поступать от остывающей воды, лед тает. При этом он получает количество теплоты

Q3 = m2O.

275

В герметически закрытом сосуде находится 5 моль

Физика для старшеклассников и абитуриентов

Далее, вода, образовавшаяся из растаявшего льда и потому имеющая такую же массу m2, начнет нагреваться от t0 = 0 0С до искомой температуры t и при этом получит количество теплоты

Q4 = c1m2(t – t0).

Теперь запишем закон сохранения тепловой энергии:

Q1 = Q2 + Q3 + Q4 ,

в который подставим вместо количеств теплоты правые части предыдущих равенств:

c1m1(t1 – t) = c2m2(t0 – t2) + m2O + c1m2(t – t0) .

Полученное уравнение называется уравнением теплового баланса. Из него, раскрыв скобки там, где есть искомая температура t, найдем ее, поскольку остальные величины нам известны:

c1m1t1 – c1m1t = c2m2(t0 – t2) + m2O + c1m2t – c1m2t0 .

Последний член этого уравнения c1m2t0 = 0, т.к. t0 = 0. Из оставшегося выражения найдем t:

t = c1m1t1 −m(2 (c2 (t0 −)t2 )+ λ ) . c1 m1 +m2

Мы решили задачу в общем виде. Произведем вычисления:

t = 4,2 103 3 40 − 0,05(2,1 103 (0 −(−4))+ 3,3 105 ) 0С | 38 0С. 4,2 103 (3 + 0,05)

Ответ: t | 38 0С.

В16. В герметически закрытом сосуде находятся 5 моль идеального одноатомного газа при 27 0С. Какое количество теплоты надо передать этому газу, чтобы его давление увеличилось в 3 раза?

Обозначим Q количество молей газа, t1 — его первоначальную температуру по шкале Цельсия, р1 —начальное давление газа, р2 — конечное давление газа, Q — количество теплоты, которое надо передать газу, ‘U — изменение внутренней энергии газа, А — работу расширения газа, R — молярную газовую постоянную, Т1 — начальную температуру газа по шкале Кельвина, Т2 — конечную температуру газа по шкале Кельвина, ‘Т — изменение температуры.

276

Раздел II. Молекулярная физика и термодинамика

Дано:			Решение

Q = 3 моль			Применим для решения этой задачи первый
t1 = 27 0C			закон термодинамики:
ð2		= 3	Q = ‘U + A.
ð	Но работа расширения газа здесь равна
1
нулю, ведь газ находится в закрытом сосуде и
		Q — ?
его объем не меняется. Значит, первый закон

термодинамики в нашем случае примет вид:
Q = ‘U,
где изменение внутренней энергии газа
‘U = 32 νR T .	(1)

Теперь задача сводится к нахождению изменения температуры ‘Т = Т2 – Т1. Нам известно, во сколько раз повысилось давление газа в закрытом сосуде вследствие нагревания, поэтому мы воспользуемся законом Шарля:

ð2	=	Ò2	или		ð2	= Ò1 + Ò = 1+	Ò .

ð1		Ò1		ð1		Ò1	Ò1
Согласно условию					ð2	= 3, поэтому 3 = 1+		Ò	,
					ð1
								Ò

1
откуда		‘Т = 2Т1.			(2)

Подставив равенство (2) в формулу (1), мы решим задачу в общем виде:

Q = U = 32 νR 2T1 = 3νRT1.

Задача в общем виде решена. Выразим температуру в единицах СИ: 27 0С = 300 К.

Произведем вычисления:

Q = 3 · 5 · 8,31 · 300 Дж | 3,7 · 104 Дж | 37 кДж.

Ответ: Q | 37 кДж.

В17. Какое количество теплоты нужно передать 2 моль идеального одноатомного газа, чтобы изобарно увеличить его объем в 3 раза, если начальная температура 300 К?

Обозначим Qколичество молей газа (количество вещества), V1 — начальный объем газа, V2 — конечный объем газа, Т1 —

277

Физика для старшеклассников и абитуриентов

начальную температуру газа, Т2 — конечную температуру газа, Q — переданное количество теплоты, р — давление газа, ‘U — изменение внутренней энергии газа, А — работу изобарного расширения газа, R — молярную газовую постоянную.

Дано:	Решение

Q = 2 моль	Согласно первому закону термо-
V2 = 3V1	динамики
р = const	Q = ‘U + А.
T1 = 300 K	Изменение внутренней энергии
R = 8,31 Дж/(моль · К)
	‘U = 3 νR (T2 − T1 ).


Q — ?	2
	Работа изобарного расширения

А = р(V2 – V1).

Согласно уравнению Менделеева — Клапейрона

р(V2 – V1) = QR(Т2 – Т1) = А.
С учетом этого
Q = 3			νR (T2 − T1 ) + QR(Т2 – Т1) = 2,5QR(Т2 – Т1).
2
Температуру Т2 найдем из закона Гей-Люссака:
при р = const
V2	=		T2	,	где по условию	V2	= 3, поэтому и	T2	= 3,

V		T		V			T
1		1		1		1
откуда			Т2 = 3Т1.
С учетом этого,

Q = 2,5 QR(3Т1 – Т1) = 5QRТ1. Произведем вычисления:

Q = 5 · 2 · 8,31 · 300 Дж = 24930 Дж = 24,93 кДж.

Ответ: Q = 24,93 кДж.

В18. На рис. 166 изображен график зависимости температуры куба со стороной 10 см от выделенного им количества теплоты. Плотность вещества куба 7000 кг/м3. Определить удельную теплоемкость вещества. Ответ округлить до целого числа.

278

В герметически закрытом сосуде находится 5 моль

Раздел II. Молекулярная физика и термодинамика

Обозначим а длину стороны куба, V — его объем, m — массу куба, U— плотность меди, с — удельную теплоемкость металла, Т1 — начальную температуру, Т2 — конечную температуру, ‘Т — изменение температуры, Q — количество выделенной теплоты.

Дано:	Решение

а = 10 см = 0,1 м	Из рис. 166 следует, что при выделении
U = 7000 кг/м3	150 кДж тепла температура куба пони-
Т1 = 600 К	зилась с 600 К до 200 К.
Т2 = 200 К	Удельную теплоемкость найдем по
Q = 150 кДж	формуле
с =	Q	, где m = UV и V = а3.
			с — ?

m T

Изменение температуры ‘Т = Т1 – Т2.

С учетом этого получим:

с = ρ a3 (T1 − T2 ). Произведем вычисления:

150000

с= 7000 0,13 (600 − 200) Дж/(кг ·К) | 54 Дж/(кг ·К).

Ответ: с | 54 Дж/(кг ·К).

В19. С какой скоростью v должна вылететь из ружья свинцовая дробинка при выстреле, сделанном вертикально вниз с высоты h = 50 м, чтобы при ударе о камень она полностью расплавилась? Начальная температура дробинки T1 = 400 K, температура плавления свинца T2 = 600 K. Удельная теплоемкость свинца c = 0,13 кДж/(кг К), удельная теплота плавления свинца O = 25 кДж/кг.

Обозначим h высоту, с которой произведен выстрел, T1 — начальную температуру дробинки, T2 — температуру плавления свинца, c — удельную теплоемкость свинца, O— удельную теплоту плавления свинца, Еk — кинетическую энергию дробинки при вылете из ружья, Еp — ее потенциальную энергию на высоте, v — скорость дробинки при вылете из ружья, Q1

— количество теплоты, полученное пулей при нагревании, Q2 — количество теплоты, полученное пулей при плавлении, m — массу пули.

279

Источник

Вы здесь

Главная » Сборник задач абитуриенту. ОСНОВЫ МКТ. Пары. Кипение. Тема 13-5

Опубликовано ср, 07/17/2019 – 22:35 пользователем fizportal.ru

ОСНОВЫ МКТ. Пары. Кипение. Тема 13-5

Во всех задачах этого раздела считайте атмосферное давление равным po = 1,013 × 105 Па. Для определения давления насыщенных водяных паров пользуйтесь таблицей.

13.73. В закрытом сосуде находятся воздух и капля воды массы m = 0,5 г. Объем сосуда V = 25 л, давление в нем 1,0 × 104 Па, температура T = 300 К. Каким станет давление p в сосуде, когда капля испарится? Температура остается неизменной.

13.74. В откачанном герметически закрытом сосуде объема V = 10 л находится открытая колбочка, содержащая m = 10 г воды. Сосуд прогревают при температуре t = 100 °С. Какая масса воды Δm испарится?

13.75. В объеме V1 = 20 л содержатся насыщенные пары воды при температуре t = 100 °С. Какую работу A надо совершить, чтобы изотермическим сжатием уменьшить объем паров до V2 = 10 л? Объемом воды, образовавшейся при конденсации, пренебречь.

13.76. Под колоколом насоса находится стакан, содержащий воду массы m = 200 г. Насос откачивает воздух из-под колокола со скоростью u = 50 л/мин. Через сколько времени вся вода испарится, если установившаяся под колоколом температура равна T = 280 K?

13.77. В запаянной трубке объема V = 0,40 л находится водяной пар под давлением p = 8,5 × 103 Па при температуре T = 423 K. Какое количество росы выпадет на стенках трубки при охлаждении ее до температуры T/ = 295 К?

13.78. Сосуд объема V = 20 дм3 разделен тонкой подвижной перегородкой на две части. В левую часть помещена вода ($nu_1$ = 1 моль), в правую − азот ($nu_2$ = 0,5 моль). Температура поддерживается равной T = 373 К. Определите объем правой части сосуда V.

13.79. Сосуд объема V = 120 дм3 разделен тонкой подвижной перегородкой на две части. В левую помещена вода (ν1 = 2 моль), в правую азот (ν2 = 1 моль). Температура поддерживается равной T = 373 К. Определите объем правой части сосуда V.

13.80. Под поршнем цилиндра объема V = 10 дм3 находится m = 1,9 г газообразного аммиака. Цилиндр помещен в термостат при температуре t = −57 °С. Какая масса аммиака Δm сконденсируется при сжатии газа поршнем до объема V/2? Давление насыщенного пара аммиака при t = −57 °C составляет p = 26,7 кПа. Молярная масса газообразного аммиака μ = 17 г/моль.

13.81. Под невесомым поршнем в цилиндре находится m = 1,0 кг воды при температуре t1 = 0 °C. В воду опускают кусок железа массы mo = 1,0 кг, нагретый до температуры t2 = 1100 °C. На какую высоту h поднимется поршень? Удельная теплоемкость железа c = 0,5 кДж/(кг$cdot$К). Площадь поршня S = 1000 см2. Теплоемкостью цилиндра и потерями тепла пренебречь.

13.82. В цилиндре находятся m = 18 г воды при температуре t = 0 °C; поршень сечения S = 100 см2 и массы M = 100 кг отделяет воду от атмосферы. Цилиндр нагревается до температуры t = 200 °C. На какую высоту Δh поднимется поршень?

13.83. В вертикально расположенном цилиндре под невесомым поршнем сечения S = 100 см2 находится m = 18 г насыщенного водяного пара. В цилиндр впрыскивают M = 18 г воды при температуре t = 0 °C. На какую высоту Δh опустится поршень?

13.84. В вертикально расположенном цилиндре под поршнем массы M = 10 кг находится некоторое количество воздуха, воды и водяного пара при температуре t = 100 °C. В положении равновесия поршень находится на расстоянии h = 20 см от дна цилиндра. Когда цилиндр расположили горизонтально, поршень занял новое положение равновесия, сместившись на Δh = 3,0 см от первоначального положения. Какая масса воды Δm была на дне сосуда? Площадь поршня S = 400 см2.

13.85. В откачанный сосуд объема V = 1,0 дм3 ввели водород до давления p2 = 266 гПа при температуре t = 20 °C. В другой такой же сосуд ввели кислород до давления p2 = 133 гПа при той же температуре. Оба сосуда соединили, и, после завершения переходных процессов, гремучую смесь подожгли электрическим разрядом. Определите массу Δm воды, сконденсировавшейся на стенках сосуда после его охлаждения до первоначальной температуры.

13.86. Запаянный сосуд заполнен смесью водорода и кислорода при температуре T1 = 300 K и давлении po = 1,0 × 105 Па. Парциальные давления компонентов смеси одинаковы. В сосуде происходит взрыв. Определите давление p внутри сосуда после того, как температура продуктов реакции станет равной T2 = 373 К.

13.87. Запаянный сосуд заполнен смесью водорода и кислорода при температуре T1 = 300 К и давлении po = 1,0 МПа. Парциальные давления компонентов смеси одинаковы. В сосуде происходит взрыв. Определите давление p внутри сосуда после того, как температура продуктов реакции станет равной T2 = 373 К.

Источник