В изолированном сосуде смешали газ а молярная масса 20 и газ в
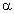
Команда “Газы!” была объявлена еще две недели назад. И что?! Легкие задачи порешали и расслабились?! Или вы думаете, что задачи на газы касаются только 28-х заданий ЕГЭ?! Как бы не так! Если газов пока еще не было в 34-х заданиях, это ничего не значит! Задач на электролиз тоже не было в ЕГЭ до 2018 года. А потом как врезали, мама не горюй! Обязательно прочитайте мою статью “Тайны задач по химии? Тяжело в учении – легко в бою!”. В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я – зритель в первом ряду.
Однако, вернемся к нашим баранам, вернее, Газам. Я прошла через огонь и воду вступительных экзаменов и знаю точно – хочешь завалить абитуриента, дай ему задачу на Газы. Почитайте на досуге сборник задач И.Ю. Белавина. Я процитирую одну такую “мозгобойню”, чтобы вам жизнь медом не казалась. Попробуйте решить.
И.Ю. Белавин, 2005, задача 229
“Два из трех газов (сероводород, водород и кислород) смешали и получили газовую смесь, плотность которой оказалась равной плотности оставшегося газа. Полученную газовую смесь вместе с равным ей объемом третьего газа под давлением поместили в замкнутый сосуд емкостью 4 л, содержавший азот при н.у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)”
Ну как, решили? Нет?! А ваши репетиторы?! Извините, это был риторический вопрос. Кстати, мои ученики, абитуриенты 2003-2008 гг. такие задачи щелкали, как семечки, на экзаменах во 2-й медицинский (теперь РНИМУ им. Н.И. Пирогова). Надеюсь, вам понятно, что 34-м задачам ЕГЭ еще есть куда усложняться, perfectio interminatus est (нет предела совершенству), с газами нужно работать, работать и работать. Поэтому команду “Газы!” отменять рано. Итак, поехали!
Сегодня мы поговорим о газовых смесях, затронем понятие плотности газа (абсолютной и относительной), средней молярной массы, решим задачи: определение средней молярной массы и плотности газа по компонентам смеси и наоборот.
• Газовая смесь – смесь отдельных газов НЕ вступающих между собой в химические реакции. К смесям газов относятся: воздух (состоит из азота, кислорода, углекислого газа, водяного пара и др.), природный газ (смесь предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и др.), дымовые газы (содержат азот, углекислый газ, пары воды, сернистый газ и др.) и др.
• Объемная доля – отношение объема данного газа к общему объему смеси, показывает, какую часть общего объема смеси занимает данный газ, измеряется в долях единицы или в процентах.
• Мольная доля – отношение количества вещества данного газа к общему количеству вещества смеси газов, измеряется в долях единицы или в процентах.
• Плотность газа (абсолютная) – определяется как отношение массы газа к его объему, единица измерения (г/л). Физический смысл абсолютной плотности газа – масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.
• Относительная плотность газа (плотность одного газа по другому) – это отношение молярной массы данного газа к молярной массе того газа, по которому она находится
• Средняя молярная масса газа – рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей
Настоятельно рекомендую запомнить среднюю молярную массу воздуха Мср(в) = 29 г/моль, в заданиях ЕГЭ часто встречается.
Обязательно посетите страницу моего сайта “Изучаем Х-ОбХ-04. Закон Авогадро. Следствия из закона Авогадро. Нормальные условия. Молярный объем газа. Абсолютная и относительная плотность газа. Закон объемных отношений” и сделайте конспекты по теории. Затем возьмите бумагу и ручку и решайте задачи вместе со мной.
ВАНГУЮ: чует мое сердце, что ЕГЭ по химии 2019 года устроит нам газовую атаку, а противогазы не выдаст!
Задача 1
Определить плотность по азоту газовой смеси, состоящей из 30% кислорода, 20% азота и 50% углекислого газа.
Задача 2
Вычислите плотность по водороду газовой смеси, содержащей 0,4 моль СО2, 0,2 моль азота и 1,4 моль кислорода.
Задача 3
5 л смеси азота и водорода имеют относительную плотность по водороду 12. Определить объем каждого газа в смеси.
Несколько задач со страницы моего сайта
Задача 4
Плотность по водороду пропан-бутановой смеси равна 23,5. Определите объемные доли пропана и бутана
Задача 5
Газообразный алкан объемом 8 л (н.у.) имеет массу 14,28 г. Чему равна его плотность по воздуху
Задача 6
Плотность паров альдегида по метану равна 2,75. Определите альдегид
Ну как? Пошло дело? Если туго, вернитесь к задачам и решайте их самостоятельно до тех пор, пока не щелкнет! А для стимуляции – десерт в виде еще одной задачи И.Ю. Белавина на газы. Наслаждайтесь ее решением самостоятельно!
И.Ю. Белавин, 2005, задача 202
“Сосуд емкостью 5,6 л при н.у. заполнили метаном, затем нагрели до высокой температуры, в результате чего произошло частичное разложение метана. Определите массу образовавшейся сажи, если известно, что после приведения к нормальным условиям объем полученной газовой смеси оказался в 1,6 раза больше объема исходного метана, эта газовая смесь обесцвечивает бромную воду и имеет плотность по воздуху 0,2931. (Ответ: m(C) = 0,6 г)”
Задачи И.Ю. Белавина – это крутой драйв! Попробуйте порешать, и вы откажетесь от просмотра любых ужастиков, поскольку запасетесь адреналином надолго! Но нам нужно спуститься на землю к ЕГЭ, простому и надежному, как первый советский трактор. Кстати, у меня в коллекции припасено немало сюрпризов с газовыми фишками, собранными за все годы работы и бережно хранимыми. Думаю, пришло время сказать им: “И снова здравствуйте!”, поскольку ЕГЭ с каждым годом становится “все чудесатее и чудесатее”. Но это уже совсем другая история. Читайте мои статьи – и вы подстелите соломку под свою ЕГЭшную попу.
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии https://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Позвоните мне +7(903)186-74-55, приходите ко мне на курс, на бесплатные Мастер-классы “Решение задач по химии”. Я с удовольствием вам помогу.
Репетитор по химии и биологии кбн В.Богунова
Источник
В.Б.ДРОЗДОВ, г. Рязань
Краткая теория. Взаимодействие молекул идеального газа друг с другом происходит путём абсолютно упругих соударений. Суммарный объём молекул пренебрежимо мал по сравнению с объёмом, занимаемым газом. Идеальный газ подчиняется уравнению Клапейрона-Менделеева:
(1)
где p, V, T – соответственно давление, объём и абсолютная температура газа, m и M – масса и молярная масса газа, – универсальная (т.е. одинаковая для разных газов) газовая постоянная. Величина называется количеством вещества и выражается в молях. Эта величина, как и масса, аддитивна, т.е. суммируется. Поэтому уравнение (1) для смеси n газов примет вид
Молярная масса конкретного газа определяется по формуле , где Mr – определяемая по таблице Менделеева относительная молекулярная масса.
Закон сохранения и превращения энергии с учётом тепловых явлений – первое начало (закон) термодинамики: количество теплоты, подведённое к телу, равно изменению внутренней энергии тела плюс работе, совершаемой телом над внешними телами, т.е.
Задача 1. Два сосуда, содержащие один и тот же газ, соединены трубкой с краном. Объёмы сосудов равны V1 и V2, а давления в них p1 и p2. Каким будет давление газа после открытия крана соединительной трубки? Температура газа в обоих сосудах одинакова и не изменяется после открытия крана.
Решение. Запишем уравнение (1) для газа в обоих сосудах до открытия крана, а затем уравнение состояния газа в едином сосуде после его открытия. Эти уравнения образуют систему:
где m1 и m2 – массы газа в первом и втором сосудах соответственно. Сложив почленно первые два уравнения и сравнив получившееся уравнение с третьим, получим p(V1 + V2) = p1V1 + p2V2, откуда искомое давление
Задача показывает, что нет ничего страшного в том, что в системе уравнений неизвестных (p, m1, m2, M, T) больше, чем уравнений. Ведь от нас не требуется найти все неизвестные. Поэтому в такой ситуации не следует искать «недостающие» уравнения – их не существует.
Задача 2. Газ, масса которого равна m1, а молярная масса M1, смешали с газом, масса которого равна m2, а молярная масса M2. Найдите среднюю молярную массу смеси.
Решение. Так как количество вещества смеси газов то искомая средняя молярная масса смеси Отметим, что полученная формула легко обобщается на случай смеси n газов:
Задача 3. Трубка длиной l, открытая с обоих концов, наполовину погружена в ртуть. Трубку сверху закрывают пальцем и вынимают из ртути. Чему равна длина столбика ртути, оставшегося в трубке? Атмосферное давление уравновешивается столбом ртути высотой H.
Решение. Пусть длина столбика ртути, оставшегося в трубке, равна x. Поскольку он находится в равновесии, то сумма действующих на столбик сил равна нулю: F1 + F2 + mg = 0. Здесь mg – сила тяжести, F1 и F2 – силы давления атмосферного и разреженного воздуха над ртутью соответственно.
Из векторного равенства вытекает скалярное: F1 = F2 + mg. Так как F1 = p1S, F2 = p2S, где S – площадь сечения трубки, – плотность ртути, то имеем:
По условию, тогда В последнем уравнении два неизвестных: x и p2. Значит, нужно ещё одно уравнение. Его нам даст закон Бойля-Мариотта, записанный для воздуха в верхней половине трубки: Исключая p2 из системы уравнений
приходим к квадратному уравнению:
2×2 – 2(H + l)x + Hl = 0
с двумя положительными корнями:
Какой из них выбрать? Очевидно, что
Поэтому
Задача 4 (мехмат МГУ, 1988). На рисунке показан цикл, совершаемый над идеальным газом, причём участок 1-2 изображает изохорный процесс, 2-3 – изобарный. Температуры газа в точках 1 и 3 равны соответственно T1 = 300 К и T3 = 400 К. Найдите температуру T2 газа в точке 2. Масса газа постоянна.
Решение. Сначала запишем уравнение для трёх вершин треугольника:
Пользуясь рисунком, меняем индексы у величин p3 и V2:
Далее исключаем неизвестную величину , которую не требуется определять:
Осталось воспользоваться несколько скрытым условием задачи: точки 0, 1, 3 лежат на одной прямой, следовательно,
Но p3 = p2, следовательно, левые части уравнений в последней системе равны. Тогда равны и правые части: откуда T2 = 346 К.
Задача 5 (МГТУ им. Н.Э.Баумана). Посередине лежащего на боку заполненного газом запаянного цилиндрического сосуда длиной L = 1 м находится тонкий поршень массой m = 0,1 кг и площадью S = 10 см2. Если сосуд поставить на основание, то поршень перемещается на расстояние l = 1 см. Каково было начальное давление p газа в сосуде? Трение между стенками сосуда и поршнем отсутствует.
Решение. Рассмотрим сосуд в горизонтальном и вертикальном положениях. Запишем по закону Бойля-Мариотта два уравнения, дополнив их условием механического равновесия поршня:
Выразим из первого уравнения p1, из второго – p2 и подставим эти величины в третье уравнение. В результате найдём из линейного уравнения искомое неизвестное:
p = 2,5•104 Па.
Задача 6. Зимой в комнате был включён электронагреватель мощностью 1 кВт, который работал 1 ч. Найдите изменение внутренней энергии воздуха в комнате.
Решение. Окружающий нас воздух представляет собой смесь двухатомных газов, если правомерно пренебречь ничтожной примесью инертных газов. Тогда внутренняя энергия воздуха
С учётом формулы (1) Объём комнаты V = const. А что будет с давлением? Отметим, что реальное жилище – не наглухо изолированный от внешнего мира бункер. Как только включили нагреватель, давление слегка повысится по сравнению с атмосферным. Воздух через мельчайшие щёлочки начнёт выходить из комнаты. Давления внутри и вне тут же сравняются. Так что и p = const. Но тогда и U = const, следовательно, изменение внутренней энергии А нагреватель включили не для увеличения внутренней энергии воздуха, а чтобы в комнате повысилась температура!
Задача 7 (физфак МГУ, 1977). Идеальный газ медленно переводят из состояния с объёмом V1 = 32 л и давлением p1 = 4,1•105 Па в состояние с объёмом V2 = 9 л и давлением p2 = 15,5•105 Па так, что давление во время сжатия изменяется в зависимости от объёма по линейному закону p = aV + b, где a и b – постоянные величины. При каком объёме температура газа в этом процессе будет наибольшей?
Решение. Имеем систему уравнений:
из которой последовательно исключаем b и a:
откуда
Из последнего уравнения и уравнения (1) легко вывести: Зависимость температуры от объёма представляет собой квадратичную функцию с отрицательным коэффициентом (при заданных значениях p1, V1, p2, V2) при старшем члене. Значит, наибольшее значение температуры достигается при
Задача 8. Некоторую массу m идеального газа с молярной массой M нагревают под поршнем так, что его температура, изменяясь пропорционально квадрату давления, возрастает от первоначального значения T1 до T2. Определите работу, совершённую газом.
Решение. Из системы уравнений
где выражаем давление:
где k = const. Видим, что давление прямо пропорционально объёму, т.е. непостоянно. В таком случае работа определяется с помощью интеграла:
Однако для линейных функций удобнее строить их графики в системе координат (p, V) и находить работу как площадь трапеции под графиком. По формуле площади трапеции (обычной, а не криволинейной):
По формуле (1):
Кроме того, p1V2 – p2V1 = kV1V2 – kV2V1 = 0.
Следовательно,
Задача 9 (МФТИ, 1976). В цилиндре под лёгким поршнем находится m = 14 г азота при T = 300 К. Какое количество теплоты необходимо ему сообщить при изотермическом увеличении объёма на = 4%?
Решение. По первому началу термодинамики, Но в изотермическом процессе для идеального газа U = const, откуда Значит, Q = A.
При T = const вычислить работу без интеграла, вообще говоря, нельзя. Однако, учитывая, что в первом приближении заменяем криволинейную трапецию обычной.
Имеем:
Так как
Из уравнения pV = p0V0 выражаем p:
Следовательно,
Q = 48,8 Дж.
Интересно сравнить приведённое решение с точным решением, полученным с применением интеграла:
Разлагая натуральный логарифм в ряд: – и ограничиваясь тремя первыми членами, получим
Таким образом, относительная погрешность составляет всего 3
Окончание следует
Источник
