В медный сосуд массой m1 нагретый

Архив для Декабрь 21st, 2011 года
Определите внутреннюю энергию газа
идеальный одноатомный газ взятый в количестве v=2кмоль переводят из одного состояния в другое. При этом температура газа в обоих состояниях одинакова t=27 oC. Определите внутреннюю энергию газа в обоих состояниях ее изменения и работу совершенную газом при этом переходе если известно что газу сообщили количество теплоты Q=10 кдж
Определите удельную теплоёмкость сосуда.
Рубрики: Задачи | 21 декабря 2011 | Bivanes
в медный сосуд , нагретый до t=350 градусов ,положили m2=600г льда при t2=-10 градусов. В результате в со суде оказалось m3=550г льда, смешанного с водой.Определите удельную теплоёмкость сосуда m1.
Термодинамика
Рубрики: Задачи | 21 декабря 2011 | Bivanes
Найти концентрацию молекул идеального одноатомного газа в сосуде вместимостью V=2л при t=27 градусов если его внутренняя энергия U=300Дж.
Определите массу сосуда
В медный сосуд,нагретый до температуры t1=350 oС положили m2=600г льда при температуре t2= -10oC.В результате в сосуде
оказалось m3=550 г льда,смешанного с водой.Определите массу сосуда m1.
Какова была скорость пули?
свинцовая пуля после удара о стену полностью расплавилась. Какова была скорость пули? начальная температура 35С удельная теплоемкость 140, удельная теплота плавления 2,4*10000.
Какова относительная влажность
Какова относительная влажность воздуха при 17С, если точка росы 10С
Определите необходимое количество
Смесь, состоящую из воды массой 800г и льда массой 250г, находящуюся при температуре 0С, необходимо нагреть до температуры 55С путем пропускания пара, температура которого 100С.
Определите необходимое количество пара ( в кг).
Физика в опытах
Лучший способ познать тот или иной закон физики — провести опыт. Но порою демонстрационных приборов для такой работы либо не хватает, либо нет вообще. Но ведь некоторые из них можно изготовить самим, даже из подручных материалов. Вот об устройстве некоторых таких приборов «Мастерок» и расскажет сегодня.
Первый прибор (рис. 1) предназначен для демонстрации вынужденных колебаний и механического резонанса.

Из курса физики известно, что вынужденные колебания любого тела появляются под влиянием внешней, периодически действующей силы. Изменяя частоту колебаний, можно добиться такого состояния, при котором частота собственных колебаний маятника совпадает с частотой вынужденных колебаний. Это явление называется резонансом. Таким образом, нетрудно показать, что вынужденные колебания тесно связаны с явлением резонанса.
Подробнее…
“Пружинная” ракета
Наша игрушка называется так потому, что ранета взлетает под действием силы пружины. Но пружина находится не внутри ракеты, а на стартовой установке.
Внешне игрушка напоминает макет небольшого полигона со стоящей на пусковом устройстве ракетой. Вблизи устройства расположен домик для «команды». От домика к пусковому устройству подходит металлический штырь — это пусковой крючок. Стоит потянуть его за колечко на конце, как ракета взлетает вертикально вверх. Высота подъема ракеты зависит от силы толчка пружины, установленной под ракетой.

Подробнее…
Источник
При работе со своими учениками, у меня накапливается много задач. Поэтому я публикую разборы задач в свободный доступ, стараюсь делать это максимально подробно и понятно, чтобы начинающие могли прочитать и разобраться в нужной для них теме. Ну а за подробными индивидуальными консультациями и репетиторством вы можете написать в мою группу в вк или в личные сообщения. Также большое количество разборов задач вы сможете найти в моей группе Репетитор IT mentor
Задача 1. На тело массой 100 кг, лежащее на наклонной плоскости, которая образует с горизонтом угол 40°, действует горизонтальная сила 1500 Н. Определить:
1) силу, прижимающую тело к плоскости;
2) силу трения тела о плоскость;
3) ускорение, с которым поднимается тело. Коэффициент трения k = 0.10; g = 10м/с².
Задача 2. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Найти ускорение тела, если на него действует сила тяжести P, а коэффициент трения между телом и плоскостью равен k . При какой величине силы F движение будет равномерным.
Задача 3. Два шара массами m1 = 2.5 кг и m2 = 1.5 кг движутся навстречу друг другу со скоростями v1 = 6 м/c и v2 = 2 м/c . Определить: 1) скорости шаров после удара; 2) кинетические энергии шаров до и после удара; 3)энергию, затраченную на деформацию шаров при ударе. Удар считать прямым, неупругим.
Прикрепляю очередной разбор задачи по физике по теме закона сохранения импульса. Неупругие шары после удара не восстанавливают свою первоначальную форму. Таким образом, сил, которые отталкивали бы шары друг от друга, не возникает. Это значит, что после удара шары будут двигаться вместе (слипшись) с одной и той же скоростью . Эту скорость определим по закону сохранения импульса. Так как шары двигаются по одной прямой, то можно записать импульс системы до удара и после удара. Считаем, что в задаче не действует диссипативных сил (сил трения, сопротивления воздуха и т.д.), поэтому импульс вдоль оси Ox сохраняется, тогда (смотри решение на картинке). Расписал довольно подробно, но если что-то не будет понятно, то задавайте вопросы в комментариях.
Задача 4. Диск массой m, радиус которого R , вращается с угловой скоростью ω0 вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. После прекращения действия на него силы диск останавливается в течение времени t. Определить угловое ускорение диска и тормозящий момент, действующий на него.
Задача 5. Два тела массами m1 и m2 связаны нитью, перекинутой через блок массой M . Найти ускорение тел, считая блок сплошным диском.
Задача 6. Шар катится по горизонтальной поверхности со скоростью v . На какую высоту h относительно своего первоначального положения поднимется шар, если он начнет вкатываться на наклонную плоскость без проскальзывания?
Задача 7. На краю вращающейся с угловой скоростью ω0 платформе стоит человек массой m. После того, как человек перешёл в другую точку платформы, угловая скорость её вращения стала равной ω. Найти расстояние от оси вращения до человека, считая платформу диском массой M и радиусом R.
Задача 8. Тело массой m брошено со скоростью v0 под углом α к горизонту. Найти кинетическую и потенциальную энергию тела в высшей точке траектории.
Задача 9. На горизонтальной поверхности находятся два тела массами m1 = 10 кг и m2 =15 кг, связанные нитью. К телу массой m2 прикладывают силу F = 100 Н, направленную под углом α = 60° к горизонту. Определить ускорение грузов и силу натяжения нити, соединяющей грузы. Трением пренебречь. (обязательно указать все силы на чертеже!)
Задача 10. На поверхности стола лежит груз массой m2 = 2 кг. На нити, прикрепленной к грузу m2 и перекинутой через невесомый блок, подвешен груз m1 = 1 кг. Коэффициент трения груза о поверхность стола 0,2. Найти ускорение грузов и силу натяжения нити.
Задача 11. Лодка массой 200 кг и длиной 3 м стоит неподвижно в стоячей воде. Мальчик массой 40 кг в лодке переходит с носа на корму. Определите, на какое расстояние при этом сдвинется лодка.
Считаем, что в нашей задаче не действует внешних сил, поэтому по теореме о центре массы системы грузов, можно считать, что координаты центра масс сохраняются в проекциях на ось OX (по оси OY движения не происходит). Проведем ось Y(ноль оси X) через центр лодки, тогда можно записать координаты человека и лодки до перехода человека с носа на корму.
Задача 12. Шарик массой 5 кг подвешен на нити. Нить может выдержать максимальное натяжение 100 Н. На какой минимальный угол от положения равновесия нужно отклонить нить с шариком, чтобы он оборвал нить, проходя через положение равновесия? (обязательно сделать рисунок, указать действующие силы!)
Задача 13. Два неупругих шара массами m1=2 кг и m2=3 кг движутся со скоростями соответственно v1=8 м/c и v2=4м/с. Определить количество теплоты, выделившееся при их столкновении. Рассмотреть 2 случая: 1) шары движутся навстречу друг другу; 2) меньший шар догоняет больший.
Задача 14. Тело совершает гармонические колебания по закону x(t) = 50⋅sin(π/3⋅t) (см). Определить полную энергию тела, если его масса 0,2 кг. Какая сила действует на тело в момент времени t = 0,5 с?
Задача 15. Два математических маятника, длины которых отличаются на Δℓ =16 см, совершают за одно и то же время: один − 10 колебаний, другой − 6 колебаний. Определить длины маятников.
Задача 16. Определить, сколько молей и молекул водорода содержится в объёме V = 5 м³ под давлением Р = 767 мм.рт.ст. при температуре t = 18 ° С. Какова плотность газа?
Задача 17. Сколько кислорода выпустили из баллона ёмкостью 1 дм3, если давление его изменилось от 14 атм до 7 атм, а температура от 27°С до 7 °С ?
Задача 18. В сосуде объёмом V = 2 м³ находится смесь m1 = 4 кг гелия и m2 = 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
Задача 19. В сосуде содержится смесь газов: гелия массой 12 г и водорода массой 2 г, температура в сосуде 77°С, давление 20 кПа. Определить молярную массу и плотность смеси газов.
Задача 20. Гелий массой 20 г нагрели от 100°С до 400°С, причем газу была передана теплота 30 кДж. Найти изменение внутренней энергии гелия и совершенную им работу.
Задача 21. При изотермическом расширении от 0,1 м3 трех молей газа его давление меняется от 4,48 атм до 1 атм. Найти совершаемую при этом работу и температуру, при которой протекает процесс.
Задача 22. Моль идеального газа, имевший первоначально температуру 300ºК, расширяется изобарически до тех пор, пока его объем не возрастет в 3 раза. Затем газ охлаждается изохорически до первоначальной температуры. Определить суммарное получаемое газом количество теплоты. Обязательно нарисовать графики процессов.
Задача 23. Азот массой m = 1 кг занимает при температуре Т1 = 300 К объём V = 0,5 м³. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определить конечный объём газа и конечную температуру.
Задача 24. Газ расширяется адиабатически, причём объём его увеличивается вдвое, а термодинамическая температура падает в 1,32 раза. Какое число степеней свободы i имеют молекулы этого газа?
Задача 25. Баллон ёмкостью V = 20 л с кислородом при давлении Р = 107 Па и температуре t1 = 70 ºС нагревается до температуры t2 = 270 ºС. Какое количество теплоты при этом поглощает газ?
Задача 26. Азот, занимающий при давлении, равном Р1 = 10⁵ Па объём V1 = 10 л, расширяется вдвое. Найти конечное давление и работу, совершённую газом в процессах: а) изобарном; б) изотермическом; в) адиабатном.
Задача 27. Кислород, масса которого 200 г, нагревают от температуры Т1 =300 К до Т2 = 400 К. Найти изменение энтропии, если известно, что начальное и конечное давление газа одинаковы и близки к атмосферному.
Задача 28. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 1,5∙10⁵ Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 260 К. Найти КПД машины, количество теплоты Q1, получаемое машиной за один цикл от нагревателя, и количество теплоты Q2, отдаваемое за один цикл холодильнику.
Задача 29. Найти суммарную кинетическую энергию Е поступательного движения всех молекул, содержащихся в объёме V = 1 дм³ газа при атмосферном давлении.
Задача 30. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 100 г водорода при температуре 400 К ? Чему равна полная внутренняя энергия газа?
Спасибо, что дочитали до конца, дорогие подписчики 🙂 Если вам интересен подобный контент и разборы задач, то оставляйте обратную связь в виде лайков и комментариев.
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в Telegram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Источник
Здесь речь следует вести не об ИЗМЕРЕНИИ, а о ВЫЧИСЛЕНИИ массы пара на основе теплового баланса.
Водяной пар приносит тепло и ОТДАЕТ его льду и медному сосуду. Те нагреваются, т.е. ПОЛУЧАЮТ тепло. Тепловой баланс в такого рода задачах “количества ОТДАННОГО (одним телом или несколькими телами) И ПОЛУЧЕННОГО (другим телом или другими телами) тепла равны”, т.е. Qотд.=Qпол.
Какие же процессы связанные с передачей тепла происходят?
Задача сформулирована недостаточно четко, так как не оговорены строго все нюансы, которые могут повлиять на решение задачи. Ну это общая беда современных задачников. Их составители неграмотны и не вникают в суть задачи, и текст задачи формулируют весьма поверхностно.
1) Так, в частности, не указано, что исходная температура медного сосуда равна температуре содержащегося в ней льда. Это конечно подразумевается, но всё равно ДОЛЖНО быть указано в условии задачи.
2) Не указан полный объем сосуда (т.е. невозможно вычислить, сколько в нем воздуха). А ведь он тоже нагревается, и забирает часть тепла. Кроме того, какая-то часть водяного пара хоть и остынет до 35 градусов, но тем не менее, останется в виде пара. Поэтому не весь пар отдаст всё содержавшееся в нём тепло. Конечно всем этим можно пренебречь, но это ОБЯЗАТЕЛЬНО должно быть указано в условии задачи.
3) Теплоемкости всех участвующих в теплообмене тел не постоянны, а изменяются при изменении температуры. Конечно, для расчетов можно взять нечто среднее, но это ОБЯЗАТЕЛЬНО должно быть указано в условии задачи.
Но всё же простим автору неграмотную формулировку задачи и будем решать принимая дополнительно следующие условия:
1) Исходную температуру сосуда принять равной температуре льда, т.е. -10 °C.
2) Принять, что теплоемкости всех участвующих в теплообмене тел постоянны в указанном интервале температур.
3) Принять, что весь участвующий в теплообмене водяной пар сконденсируется, т.е. не останется насыщенного при температуре 35 °C пара.
4) Принять, что содержащийся в сосуде воздух не нагреется, или лучше так: пренебречь нагревом содержащегося в сосуде воздуха от -10 до 35 °C.
Тогда можно приступить к решению задачи.
Что происходит с паром?
1) Пар сконденсируется при его исходной температуре (100 °C). При этом он отдаст количество тепла Q1=r*m1, где Q1 – теплота конденсации пара кДж, r – удельная теплота конденсации пара (испарения воды) при 100 °C (кДж/кг), m1 – масса водяного пара (то, что требуется вычислить).
2) Конденсат пара (вода при 100 °C) охладится до температуры 35 °C. При этом она отдаст количество теплоты Q2=c1*m1*(t1-t2) кДж, где Q2 количество тепла, выделившееся при охлаждении воды со 100 до 35 °C , c1 – средняя удельная теплоемкость воды (кДж/(кг*К) или кДж/(кг*°C)) в интервале 35…100 °C, m1 – масса охладившейся воды, равна массе впущенного пара (см. выше), t1 – начальная температура охлаждающейся воды (100 °C ), t2 – конечная температура охлаждающейся воды (35 °C ).
Итак, Qотд.=Q1+Q2= r*m1+ c1*m1*(t1-t2)=m1*(r+c1*(t1-t2)) кДж.
Что происходит со льдом?
3) Лед вначале нагревается от -10 до 0 °C. На это требуется количество тепла, равное Q3=c2*m2*(t3-t4), где Q3 – количество тепла, требующееся на нагревание льда от -10 до 0 °C, c2 средняя удельная теплоемкость льда (кДж/(кг*К), (дана в условии 2,1*10^3 (Дж/(кг*К) или 2,1 (кДж/(кг*К), m2 – масса льда (10 кг), t3 – конечная температура нагрева льда (0 °C), t4 –начальная температура льда (-10 °C).
4) Затем лёд плавится при температуре 0 °C. На это требуется количество тепла, равное Q4=лямбда*m2 кДж, где * Q4- количество тепла (кДж), требующееся на плавление льда при 0 °C, лямбда – удельная теплота плавления льда при 0 °C (кДж/кг), m2 – масса льда (10 кг).
5) Затем, образовавшаяся при плавлении льда вода нагревается от 0 до 35 °C. На это требуется количество тепла, равное Q5=c1*m2*(t2-t3), где Q5 – количество тепла, требующееся на нагревание воды от 0 до 35 °C, c1 средняя удельная теплоемкость воды (кДж/(кг*К), m2 – масса нагреваемой воды (равна массе расплавленного льда, т.е. 10 кг), t2 – конечная температура нагрева воды (35 °C), t3 –начальная температура воды (0 °C).
Итак, на нагрев, плавление льда и нагрев образовавшейся водя затрачивается Q3+Q4+Q5= c2*m2*(t3-t4)+ лямбда*m2+ c1*m2*(t2-t3) = m2*( c2*(t3-t4)+лямбда + c1*(t2-t3)) кДж.
6) Медный сосуд нагревается от -10 до 35 градусов. На это требуется количество тепла, равное Q6=c3*m3*(t2-t4), где Q6 – количество тепла, требующееся на нагревание медного сосуда от -10 до 35 °C, c3 средняя удельная теплоемкость меди (кДж/(кг*К), m3 – масса медного сосуда (1,5 кг), t2 – конечная температура нагревасосуда (35 °C), t3 –начальная температура сосуда (-10 °C).
Итак, Qпол.= Q3+Q4+Q5+Q6= m2*( c2*(t3-t4)+лямбда + c1*(t2-t3))+ c3*m3*(t2-t4) кДж.
Подставляя в исходное уравнение теплового баланса Qотд.=Qпол., получаем:
m1*(r+c1*(t1-t2)) = m2*( c2*(t3-t4)+лямбда + c1*(t2-t3))+ c3*m3*(t2-t4).
В этом уравнении единственное неизвестное – искомая масса водяного пара (m1), остальные известные. Подставив значения, вычислим m1.
Недостающие величины (с1, r, лямбда) берутся из таблиц, которые обязательно есть в задачнике или учебнике. Если не найдете, то на всякий случай, с1= 1 ккал/(кг*°C), r=539 ккал/кг, лямбда равна 80 ккал/кг. Коэффициент пересчета ккал в кДж точно не помню (около 4,2), найдёте сами.
Источник
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
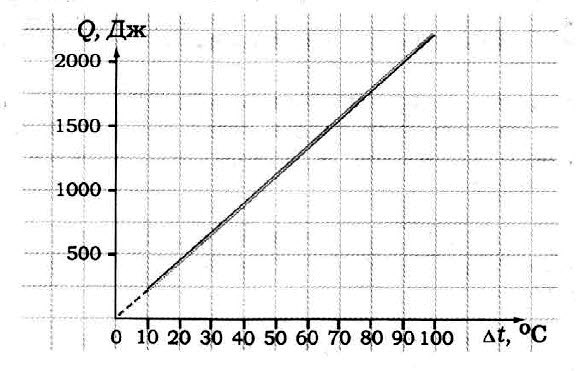

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
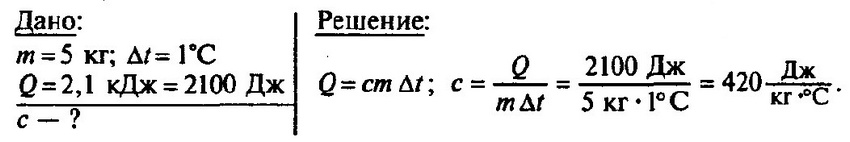
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
