В мерном сосуде находится 1 л неизвестной жидкости при

Учимся решать экспериментальные задачи: учащимся 7-10 класса, желающим участвовать в олимпиадах по физике

Физика – наука экспериментальная. Именно поэтому проведение экспериментального тура уже давно вошло в практику физических олимпиад. Выполняя задания этого тура, учащиеся должны продемон­стрировать умение своими руками создать экспериментальную уста­новку, провести на ней измерения, выявить определенные физические закономерности, оценить точность полученных результатов.

Решение экспериментальных задач воспитывает стремление собственными силами добывать знания, активно познавать Мир, приучает самостоятельно анализировать явления, заставляет напряженно думать, привлекая свои теоре­тические знания и практические навыки. Разбор экспериментальных задач воспитывает критический подход к результатам измерений, привычку обращать внима­ние на условия, при которых производится эксперимент. Экспериментальные задачи помогают лучше ре­шать расчетные, так как при решении эксперимен­тальных задач ученику приходится сначала осмыслить физи­ческое явление или закономерность, выявить, какие данные ему нужны, продумать способы и возможности их определения, найти их и только на заключительном этапе уже вполне ос­мысленно подставить в формулу.

Предлагаем несколько экспериментальных задач с решением по теме «Законы гидростатики» из числа тех, что предлагались в разное время на олимпиадах по физике самого разного уровня: от городского до российского.

Экспериментальные задачи

Задача 1. Определите плотность деревянного бруска.

Оборудование: линейка, сосуд с водой, мерный стакан.

Указание. Воспользуйтесь условием плавания тела: если тело плавает, значит, сила тяжести равна выталкивающей силе.

Возможное решение. Заполним сосуд (рекомендуется взять пластиковую тарелку) водой насколько это возможно. Пусть объ­ем жидкости равен Vтaр. Аккуратно опустим брусок в пластиковую тарелку с водой. Объем вытесненной воды V1 определим с помощью мерного стакана. Ак­куратно погрузим весь брусок в воду. Некоторая часть воды вновь выльется из тарелки. Ясно, что всего из тарелки будет вытеснен объем воды равный объему бруска Vбрус. ρвV1= Vбрусρбрус Þ ρбрус = ρвV1/Vбрус. Несмотря на идейную простоту, задача требует известного эксперименталь­ного искусства и внимательности: объем воды умещающийся в тарелке оказыва­ется больше объема тарелки, т. к. заметная часть воды “возвышается” над краем тарелки за счет сил поверхностного натяжения. Небрежно выполненный экспе­римент приводит к ощутимой ошибке в определении плотности дерева.

Задача 2. Определите плотность металла, находящегося в одном из двух кусков пластилина, если известно, что массы пластилина в обоих кусках одинаковы. Оцените точность полученного результата. Извлекать металл из пластилина не разрешается.

Оборудование: весы с разновесами, стакан с водой, штатив, два одинаковых по массе куска пластилина, небольшой кусок металла или моток проволоки, введенный внутрь одного из кусков пластилина.

Возможное решение. Задача очень похожа на знаменитую задачу о короне царя Гиерона (определение наличия примесей в зо­лоте), только с более доступными материала­ми — пластилином и железом (кусок железа находился внутри пластилина).

Пользуясь весами с разновесами, можно определить массу куска пластилина с металлом (mпл+mм), массу чистого пластилина mпл и по их разности — массу металла mм, находящегося в одном из кусков пластилина. Взвесив данные куски пластилина сначала в воздухе, а потом в воде, можно найти выталкивающую силу и, зная плотноcть воды, можно вычислить объемы кусков (Vпл+Vм) и Vпл. Объем металла Vм можно определить по разности этих объемов.

Тогда плотность металла ρм= mм/Vм.

Возможны два варианта: в одних кусках пластилинa находился кусок алюминия, в других – кусок железа.

Весьма интересным было бы решение этой задачи, если бы вместо определенного куска чистого пластилина массой, равной массе пластилина в составном куске, давался просто пластилин (в неопределенном количестве). В этом случае для решения задачи надо было бы взять кусок чистого пластилина, масса которого равна массе (m) составного куска (объема V), и определить его объем V0. Плотность металла можно найти, решив следующую систему четырех уравнений с четырьмя неизвестными:

m = ρмVм+ ρплVпл

V = Vпл+Vм

V0 = Vпл+Vм

ρпл= m/ V0

Задача 3. Определите плотность тела.

Оборудование: динамометр, стакан с водой, стакан с машинным маслом, тело неправильной формы.

Возможное решение. На тело, подвешенное на нити в жидкости, действуют три силы: сила тяжести F1 = mg, архимедова сила FA и сила натяжения нити Т (рис.5).

Модуль силы натяжения равен весу тела в жидкости: ‘Г – Р. Направим координатную ось OY вертикально вверх и запишем условие равновесия тела и проекциях на эту ось: Т+ FA- Fт= 0.

Отсюда T = Fт – FA, или T = mg – ρжgV = g(m – ρжV).

Таким образом, получаем следующую формулу для веса тела массой m в жидкости с плотностью ρж: Р= g(m – ρжV).

Для двух разных жидкостей имеем:

P1= g(m – ρ1V);

P2 = g(m – ρ2V).

Разделив левые и правые части этих уравнений на gV и учтя, что ρ =, получим: = ρ – ρ1; = ρ – ρ2. Решая совместно эти уравнения, найдем плотность тела ρ = . Измерив вес тела в двух разных жидкостях с известными плотностями, рассчитаем плотность твердого тела.

Задача 4. Определите плотность неизвестной жидкости.

Оборудование: динамометр, стакан с водой, стакан с неизвестной жидкостью, грузик.

Возможное решение. Определим вес тела в двух различных жидкостях Р1 и Р2. Вес тела в жидкости равен: P1= mg – FA1 = mg – ρ1gV;

P2 = mg – FA2 = mg – ρ2gV или

mg – P1 = ρ1gV;

mg – P2 = ρ2gV.

Отсюда =; ρ2 = ρ1.

Задача 5. Найдите плотность деревянного бруска и кусочков металла.

Оборудование: мерный сосуд, деревянный брусок, мелкие кусочки металла, сосуд с водой.

Возможное решение. Пусть V0- объем воды, налитой в мерный сосуд. Опустим брусок плавать. При этом суммарный объем воды и погруженной в воду части бруска (измеренный по шкале сосуда) обозначим через V1.

Будем накладывать на брусок кусочки металла до тех нор, пока его верхняя грань не окажется на одном уровне с поверхностью воды. Новый суммарный объем воды и погруженного в воду бруска обозначим V2. Сбросим теперь кусочки металла в сосуд. Суммарный объем воды и бруска обозначим V3. Запишем условие равновесия для обеих ситуаций, когда брусок погружен в воду полностью, а кусочки металла находятся на нем, и когда кусочки металла сброшены с бруска в воду: ρбVбg = ρвgVп; ρмVмg+ ρ бVбg = ρвgVб, где ρб – плотность бруска, Vб – его объем, Vп – объем погруженной части бруска, ρм – плотность металла, Vм – суммарный объем всех кусочков металла.

ρб = ; ρм = ; => ρб = ; ρм =.

Задача 6. Определить плотность данной жидкости.

Оборудование: сосуд с неизвестной жидкостью, сосуд с водой, измеритель­ная линейка, два металлических бру­ска, рычаг.

Примечание. Плотность воды принять равной 103 кг/м3.

Возможное решение. Надо провести три измерения по установлению равновесия рычага, когда один брусок находится попе­ременно в воздухе, в воде, в неиз­вестной жидкости, а другой брусок — все время в воздухе. При этом ра­зумно длину плеча рычага с первым грузом оставлять неизменной, а дли­ну плеча рычага со вторым грузом соответственно изменять. Запишем уравнения моментов сил для трех случаев равновесия рычага (рис.6): m1gl = m2gl1,

(m1g – ρвVg) l= m2gl2, (m1g – ρVg)l = m2gl3.

Исключая из этих уравнений m1, m2, V и g, получаем формулу для опре­деления плотности ρ неизвестной жидкости (раствора медного купо­роса) : .

Задача 7. Определить плотность неиз­вестной жидкости (чуть подкрашен­ный концентрированный раствор по­варенной соли в воде).

Оборудование: небольшая колба известного объема с тонким длинным горлышком и миллиметровка. Неизвестная жидкость налита в один большой сосуд, обычная вода — в другой.

Возможное решение. Один из способов измерения: сделать из кол­бочки ареометр, налив туда некоторое количество жидкости и пустив ее плавать в сосуде с водой. Количество жидкости нужно подобрать так, чтобы над поверхностью торчало толь­ко горлышко колбы, диаметр которо­го легко измерить,— в этом случае можно произвести теоретический расчет плотности. Для достижения приемлемой точности приходится учитывать и поверхностные эффекты. В целом задача не очень сложная, но требует аккуратности в измерениях.

Задача 8. Взвешивание сверхлёгких грузов. Определить с помощью предложенного оборудования массу m кусочка фольги.

Оборудование. Банка с водой, кусок пенопласта, набор гвоздей, деревянные зубочистки, линейка с миллиметровыми делениями, остро отточенный карандаш, фольга, салфетки.

Возможное решение. Измеряем диаметр d цилиндрической части зубочистки методом рядов (положив несколько зубочисток плотно в ряд и измерив линейкой их общую ширину). На одну из зубочисток наносим карандашом через 1 мм деления.

Втыкаем в пенопласт гвоздики, пока он не погрузится в воду почти полностью. Сверху втыкаем зубочистку с делениями, чтобы пенопласт был ниже уровня воды, а зубочистка вертикально выступала из воды не меньше, чем на 3/4 длины. При необходимости от пенопласта можно отделить небольшой кусо чек. Затем на верхний конец зубочистки прикрепляем кусочек фольги (рис.7) и находим изменение Δh глубины погружения зубочистки.

Изменение объёма ΔV погруженной части: ΔV=, откуда масса фольги m=ρΔV=ρΔhd2, где ρ — плотность воды.

Рекомендации для организаторов. Для эксперимента подходит литровая банка (или двухлитровая пластиковая бутылка с отрезанным верхом), она должна быть наполнена водой почти до краёв. Зубочистки должны быть не искривлёнными, одинакового диаметра, а их длина должна быть не меньше 6 см, количество: 5 ¸ 10 штук. Размеры пенопласта: высота 0,5 ¸ 1 см, длина и ширина 2 ¸ 4 см. Размеры фольги должны быть такими, чтобы под её весом зубочистка погружалась приблизительно на 2/3 своей длины. Для пищевой фольги эти размеры составляют от 2 см х 2 см до 4 см х 4 см. Масса гвоздей должна позволять утопить пенопласт. Гвозди следует взять разного диаметра: крупные — для грубой настройки системы, а мелкие — для точной.

Задача 9. Определите массу тела.

Оборудование: пружина, тело неизвестной массы, мензурка, штатив с муфтой и лапкой, сосуд с водой, линейка измерительная.

Возможное решение. Подвесим к пружине груз неизвестной массы и измерим удлинение х, пружины. Условие равновесия груза на пружине в воздухе запишем так:

mg = kx1 (1).

Опустим груз в сосуд с водой и измерим новое удлинение х2 пружины. Условие равновесия для груза, опушенного в сосуд с водой: mg – FA = kx2 (2), где FA – архимедова сила, действующая на груз. Она равна FA = p0gV, где ρ0 – плотность воды, V – объем тела.

Измерив объем тела с помощью мензурки, используя выражения (I) и (2), рассчитаем жесткость пружины: k = и искомую массу груза: m = .

Контрольное задание по физике №3 для учащихся 7-10 классов.

Задача 10. Определите плотность растительного масла.

Оборудование: линейка, сосуд с водой, сосуд с маслом.

Указание: Плотность неизвестной жидкости (в данном случае, масла) можно определить методом сравнения масс при равных объемах или методом сравнения объемов при равных массах. Считайте плотность воды известной, равной 1000 кг/м3. Воспользуйтесь линейкой как рычагом.

Задача 11. Определить плотность дерева, из которого изготовлена палочка.

Оборудование: линейка, деревянная палочка, узкий цилиндрический сосуд с водой.

Задача 12. Определите плотность стекла, из кото­рого изготовлена банка из-под майонеза.

Оборудование: майонезная банка, мензурка объемом V=250 мм3, стеклянный сосуд, полоска из мягкого металла разме­ром 2х20 см, сосуд с водой (водопровод­ный кран).

По специальной договоренности с редколлегией и редакцией журнала «Квант»

В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).

Перейдем к обсуждению конкретных задач.

Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3

Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный

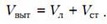
Очевидно, что этот же объем равен

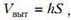
где S — площадь поперечного сечения сосуда.

Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:

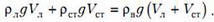
Из совместного решения полученных уравнений найдем объемы льда и стекла:

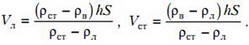
Из растаявшего льда образовалась вода объемом

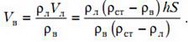
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно

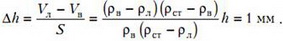
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.

Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде

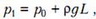
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид

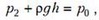
где p2 – новое давление воздуха над ртутным столбиком.

Условие сохранения количества изолированного воздуха позволяет записать

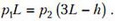
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:

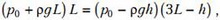
или, если записать атмосферное давление в виде , где H0 = 774 мм:

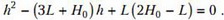
Для данных численных значений L и H0 (в мм) получается, что

h = 270 мм.

Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.

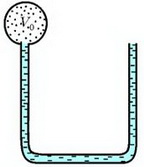
Рис. 1

Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена

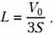
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:

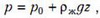
где ρж – плотность жидкости. На втором участке, для которого , давление гелия

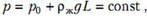
а на третьем участке, для

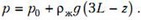
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:

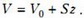
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.

Учитывая, что , запишем уравнение процесса для третьего участка в виде

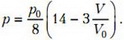
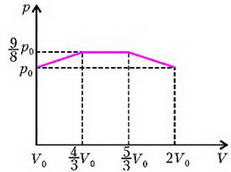
Рис. 2.

Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна

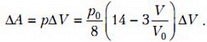
Запишем уравнение состояния гелия как идеального газа:

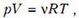
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим

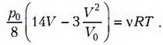
Продифференцируем обе части этого уравнения:

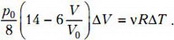
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:

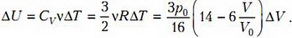
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:

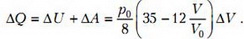
Легко убедиться, что при  и

Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:

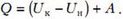
Поскольку начальная и конечная температуры равны, соответственно,

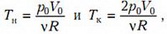
то изменение внутренней энергии равно

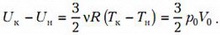
Полную работу найдем как площадь под кривой на рисунке 2:

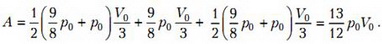
Тогда окончательно

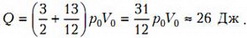
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.

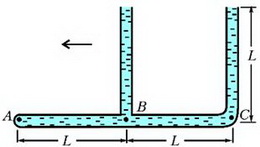
Рис. 3.

При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:

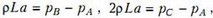
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны

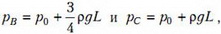
где p0 – атмосферное давление.

Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:

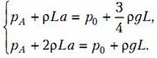
Решая эту систему относительно рА, найдем

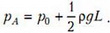
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.

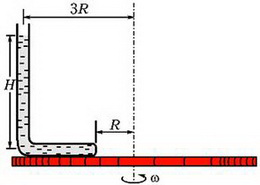
Рис. 4.

Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).

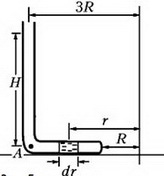
Рис. 5.

Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:

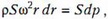
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:

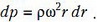
Проинтегрируем обе части этого уравнения и получим

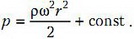
Константу определим из условия, что при r = 3R (точка А) давление равно

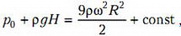
и получим зависимость p(r)

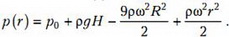
Отсюда найдем давление ртути у запаянного конца трубки (r = R):

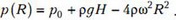
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.

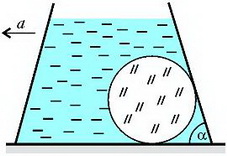
Рис. 6.

Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.

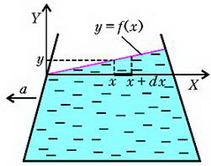
Рис. 7.

Наша задача – найти уравнение свободной поверхности жидкости  в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно

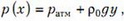
а с правого торца оно равно

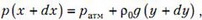
где у – высота столба жидкости в точке х, а  – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид

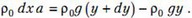
Отсюда получаем

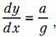
или в интегральном виде —

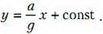
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:

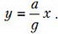
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным  и направленным под углом  к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.

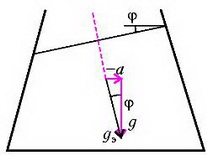
Рис. 8.

В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.

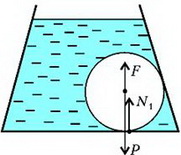
Рис. 9.

Здесь  – вес (точнее – сила тяжести) шара,  – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что

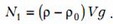
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.

В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:

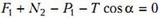
и по горизонтали:

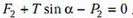
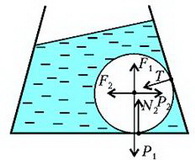
Рис. 10.

Исключая из этих уравнений Т, найдем искомую силу N2:

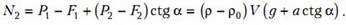
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.

Упражнения.

1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.

2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.

3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.

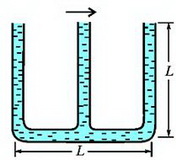
Рис. 11

4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.

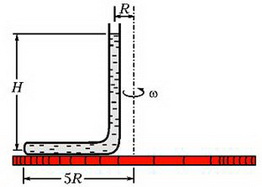
Рис. 12

Ответы.

1.

2.

3. .

4.