В некотором сосуде вместимостью 6 72 л при нормальных условиях

Никита Кнышов

19 ноября 2018 · 2,8 K

22,4 литра ———– 6.02*10²³ молекул.

5,6 литра ———– ? молекул.

Простая пропорция. Надеюсь, вы справитесь.

22,4 [л] – это объем одного моля газа при нормальных условиях.

6.02*10²³ [1/моль] – это число Авогадро.

не стоит за школьников делать их домашку…

Какой объём займёт 1 кг воздуха при 17 градусах и давлении 101.3 кпа?

к.п.н., широкий круг интересов

Воздух при данных условиях можно рассматривать как идеальный газ. Поэтому для решения задачи можно использовать уравнение Менделеева-Клапейрона (уравнение состояния идеального газа).

pV=(m/M)RT, где p – давление газа, V – объем газа, R – универсальная газовая постоянная, равная 8,31 Дж/(моль*К), m – масса газа, M – молярная масса газа (в данном случае – воздуха), равная 0,029 кг/мол.

Отсюда V = m*R*T/(M*p)

Переводим величины в основные единицы СИ

17 градусов = 290 К

101,3 кПа = 101300 Па

Таким образом V = 1 * 8.31 * 290/(0.029 * 101300)

V=0.82 (m^3)

Сколько молекул содержится в 2,5 моль кислорода?

Инженер по профессии, люблю спорт, музыку, кино.

В одном моле любого вещества всегда содержится одно и тоже число молекул, называемое числом Авогадро:

Na = 6.02*10^23

Тогда в n=2,5 моль кислорода содержится молекул:

N = n*Na = 2.5*6.02*10^23 = 15.05*10^23

Проектирование деталей из листового металла

Дизайн листового металла – это искусство, которое проникает во многие различные отрасли промышленности за его прочность и долговечность. В отличие от пластика, из листового металла можно сделать долговечный продукт, который выдерживает тепло и нагрузки, а также защищает более хрупкие детали. Среди прочего, он очень часто используется в качестве корпуса для электроники.

Листовой металл — металл в форме листов и широкиx листовыx полос, изготавливаемый прокаткой, реже — ковкой. Он может быть изготовлен из различных видов металлов, включая алюминий, латунь, медь, сталь, олово, никель и титан. Золото, серебро и даже платина также входят в состав листового металла для декоративных изделий. Проектирование изделий из листового металла имеет свои ограничения, но работа с этим конструкционным материалом имеет столько преимуществ, что они перевешивают недостатки. Например, все детали из листового металла должны начинаться с плоской детали. Окончательный вид продукта достигается за счет сгибания, резки или сварки, клепки если это необходимо для достижения окончательной формы.

Изделия из листового металла используются во многих областях:

Автомобильный дизайн;
Воздухоплавательные конструкции;
Морской дизайн;
Проектирование транспортных систем;
Медицинское оборудование и продукты;
Приборостроение;
Системы отопления и охлаждения;
Дизайн мебели;
Еда и посуда;
Архитектура и строительство;
Телекоммуникационная система;
Конструкции корпусов машин.

Машиностроение, строительная область, автомобильная промышленность и другие производственные сферы испытывают постоянную необходимость в высококачественных металлических листовых изделиях, которые соответствовали бы современным требованиям. Изготовлением деталей из листового металла по чертежам, как правило, занимаются предприятия по металлообработке.

Одна из загадок Mortal Kombat 11 была решена

Взаимная подписка, делаю сайты https://saitim.ru/

Речь о метеоре, который с определенной периодичностью пролетал на фоне в режиме «Башни времени». Многие предполагали, что для активации секрета нужно ввести определенную комбинацию, и TheThiny сумел ее найти.

Для того чтобы получить доступ к случайной особой башне, нужно при появлении метеора успеть ввести следующую команду: вверх, влево, вверх, влево, вправо, влево, вверх, вверх. Делать это нужно до того, как метеор скроется с экрана. Он пролетает на десятой минуте каждого второго часа в сутки. Для входа в открывшуюся башню нужно 250 тыс. монет, 500 сердец и 2,5 тыс. душ. При этом башня всегда открывается на максимальной сложности, поэтому рекомендуется запастись расходуемыми предметами. На ее прохождение дается час, но в случае, если игрок выйдет из режима «Башни времени», она исчезнет. За прохождение можно получить один из скинов из Kombat League, а также облик, аксессуар или костюм для персонажа, которым играет пользователь.

Источник

Задача 47.
0,350г металла вытеснили из кислоты 209 мл водорода, собранного над водой при 20 °С и давлении 104,3 кПа. Давление насыщенного пара воды при этой температуре составляет 2,3кПа. Найти эквивалентную массу металла.
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:

Обозначив искомый объём через и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим V0:

где Р и V – давление и объём газа при температуре T = 293К (273 +20 = 293); P0 = 101,325кПа; T0 = 273К; = 102кПа; V0 – объём газа при н.у..

Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):

Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:

Ответ: m(Э) = 20г/моль.

Задача 48.
250 мл водорода собраны над водой при 26°С и давлении 98,7кПа. Давление насыщенного пара воды при 26°С составляет 3,4кПа. Вычислить объем водорода при нормальных условиях и его массу.
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:

Обозначив искомый объём через V0 и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим V0:

где P и V – давление и объём газа при температуре T = 299К (273 +26 = 299); P0 = 101,325кПа; T0 = 273К; V0 = 95,3кПа; – объём газа при н.у..

Учитывая, что 1г Н2 занимает 11200 мл рассчитаем массу водорода, содержащуюся в 214,97мл, составив пропорцию:

Ответ:

Задача 49.
0,604г двухвалентного металла вытеснили из кислоты 581мл водорода, собранного над водой при 18°С и давлении 105,6 кПа. Давление насыщенного пара воды при 18°С составляет 2,1кПа. Найти относительную атомную массу металла.
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды.

где P и V – давление и объём газа при температуре T = 291K (273 + 18 = 291); T0 = 273К; P0 = 101,325 Kпа; V0 -объём газа при н.у.

Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):

Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:

Молекулярная масса металла равна произведению эквивалентной массы на валентность его:

M(Me) = mЭ(Me). B, где B – валентность металла. Тогда M(Me) = 12,16 . 2 = 24,32г/моль.

Ответ: M(Me) = 24,32г/моль.

Задача 50.
Сосуд наполнен смесью кислорода и азота. При каком соотношении парциальных давлений массы газов будут одинаковы:

Решение:
Парциальным давлением любого газа в смеси называется давление, которое производил бы газ, занимая при тех же условиях объём всей газовой смеси.

Так как 1моль любого газа занимает одинаковый объём при одинаковых физических условиях (например, 22,4л при н.у.), следовательно, и парциальные давления 1-го моля любого газа при тех же физических условиях будут одинаковы.

Молекулярная масса кислорода больше молекулярной массы азота в 1,14 раза (32/!4 = 1,14), то при одинаковых массах данных газов, соответственно, парциальное давление азота будет в 1,14 раза меньше, чем у кислорода, т. е.:

Ответ: б).

Задача 51.
Парциальное давление кислорода в воздухе равно 22 кПа. Чему равно содержание кислорода в процентах по объему: а) 42%; 6) 21%; в) 10,5%?
Решение:
Воздух представляет собой, в основном, смесь азота и кислорода. Для нахождения приведённого объёма кислорода, входящего в состав воздуха, приведённый к давлению смеси (Рвозд.) и температуре (Т) необходимо воспользоваться законом Бойля-Мариотта:

где – объём кислорода; Vвозд. – объём воздуха; Рвозд. – общее давление смеси кислорода и азота (н.у.), 101,325кПа; – парциальное давление кислорода, 22кПа.

Сумма приведённых объёмов отдельных газов в смеси равняется общему объёму смеси, т. е.:

Отношение приведённых объёмов кислорода и азота к общему объёму воздуха называется объёмной долей и обозначается через r. Тогда:

Следовательно, содержание кислорода в процентах по объёму в воздухе с учётом закона Бойля-Мариотта, равно:

Ответ: б)

Задача 52.
Водород собирали в одном случае над водой, в другом над ртутью при одинаковых условиях. В обоих случаях объем газа оказался одинаковым. Одинаковы ли количества собранного водорода: а) одинаковы; б) количество водорода, собранного над ртутью, больше; в) количество водорода, собранного над водой, больше?
Решение:
Водород собирали над водой и над ртутью при одинаковых условиях при этом объёмы обеих систем оказались одинаковы. Учитывая, что ртуть имеет большую плотность, чем вода, то можно предположить, что количество водорода, собранное над ртутью будет больше, чем собранное над водой.

В обоих случаях объём газовой смеси будет складываться из определённого объёма водорода и паров жидкости, над которой собран газ. Так как температура кипения ртути и её плотность значительно выше, чем у воды, то в равных объёмах газов водорода будет содержаться больше над ртутью, так как ртути (её паров) будет в смеси значительно меньше, чем паров воды.

Таким образом, вследствие малой испаряемости ртути по отношению к воде парциальное давление паров ртути над жидкой ртутью будет меньше, чем парциальное давление паров воды над жидкой водой при одинаковых условиях и, следовательно, парциальное давление водорода над ртутью будет больше, чем над водой. Отсюда вытекает, что количество водорода, собранного над ртутью, больше, чем над водой.

Ответ: б).

Источник

Задача 41.
Смешивают 0,04м3 азота, находящегося под давлением 96кПа (720мм. рт. ст.), с 0,02м3 кислорода. Общий объем смеси 0,06м3, а общее давление 97,6кПа (732мм. рт. ст.). Каким было давление взятого кислорода?
Решение:
По условию задачи объём азота увеличился в 1,5 раза (0,06/0,04 = 1,5), а объём кислорода – в 3 раза (0,06/0,02 = 3). Во столько же раз уменьшились парциальные давления газов.

Следовательно,

Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). Отсюда Исходя из того, что объём кислорода до смешения был в три раза больше, чем после смешения, рассчитаем давление кислорода до смешения:

Ответ: Робщ. = 100,8кПа.

Задача 42.
Газовая смесь приготовлена из 2л Н2 (Р = 93,3 кПа) и 5л CH4 (Р = 112 кПа). Объем смеси равен 7л. Найти парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём водорода увеличился в 3,5 раза (7/2 = 3,5), а объём метана – в 1,4 раза (7/5 = 1,4). Во столько же раз уменьшились парциальные давления газов.

Отсюда:

Ответ:

Задача 43.
Газовая смесь состоит из NO и СО2. Вычислить объемное содержание газов в смеси (в %), если их парциальные давления равны соответственно 36,3 и 70,4 кПа (272 и 528мм. рт. ст.).
Решение:
Согласно закону Дальтона парциальное давление данного газа прямо пропорционально его мольной доли на общее давление смеси газов:

где Р(смеси) – общее давление смеси; Р(А) – парциальное давление данного газа; (A) – мольная доля данного газа.

Отсюда:

Ответ: 34,02%NO; 65,98%CO.

Задача 44.
В закрытом сосуде вместимостью 0,6м3 находится при 0 °С смесь, состоящая из 0,2кг СО2, 0,4кг 02 и 0,15кг СН4. Вычислить: а) общее давление смеси; б) парциальное давление каждого из газов; в) процентный состав смеси по объему.
Решение:
Вычислим общее количество газов в смеси по уравнению:

, где

– количество газа, кмоль; m – масса газа, кг; М – молекулярная масса газа, кг/моль. Тогда:

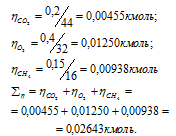
парциальное давление газа

а) Общее давление смеси газов определяем по уравнению:

Тогда:

б) Парциальные давления газов рассчитываем по уравнению:

где Rk и k , соответственно, парциальное давление, и количество газа в смеси.

Тогда

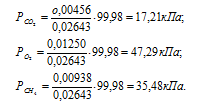
парциальное давление газа

в) Парциальные объёмы газов рассчитаем по уравнению:

Тогда

Отношение парциальных (приведённых) объёмов отдельных газов к общему объёму смеси называется объёмной долей и определяется по формуле:

Тогда

Ответ:

Задача 45.
Газовая смесь приготовлена из 0,03м3 СН4, 0,04м3 Н2 и 0,01м3 СО. Исходные давления СН4, Н2 и СО составляли ответственно 96, 84 и 108,8 кПа (720, 630 и 816мм рт. ст.). Объем смеси равен 0,08м3. Определить парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём метана увеличился после смешения в 2,67 раза (0,08/0,03 = 2,67), объём водорода – в 2 раза (0,08/0,04 = 2), а объём угарного газа – в 8 раз (0,08/0,01 = 8). Во столько же раз уменьшились парциальные давления газов. Следовательно,

Отсюда:

Ответ:

Задача 46.
В газометре над водой находятся 7,4л кислорода при 23 °С и давлении 104,1 кПа (781 мм. рт. ст.). Давление насыщенного водяного пара при 23 °С равно 2,8 кПа (21мм. рт. ст.). Какой объем займет находящийся в газометре кислород при нормальных условиях?
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:

Обозначив искомый объём через и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим:

где Р и V – давление и объём газа при температуре Т = 296К (273 +23 = 296); Р0 = 101,325кПа; Т0 = 273К; Р = 104,1кПа; – объём газа при н.у.

Ответ: V0 =6,825л.

Источник

Задача 28.
При 17°С некоторое количество газа занимает объем 580 мл. Какой объем займет это же количество газа при 100°С, если давление его останется неизменным?
Решение:
По закону Гей – Люссака при постоянном давлении объём газа изменяется прямо пропорционально абсолютной температуре (Т):

V2 – искомый объём газа;
T2 – соответствующая V2 температура;
V1 – начальный объём газа при соответствующей температуре Т1.

По условию задачи V1 = 580мл; Т1 = 290К (273 + 17 = 290) и Т2 = 373К (273 + 100 = 373). Подставляя эти значения в выражение закона Гей – Люссака, получим:

Ответ: V2 = 746мл.

Задача 29.
Давление газа, занимающего объем 2,5л, равно 121,6 кПа (912мм рт. ст.). Чему будет равно давление, если, не изменяя температуры, сжать газ до объема в 1л?
Решение:
Согласно закону Бойля – Мариотта, при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объёму газа:

Обозначив искомое давление газа через Р2, можно записать:

Ответ: Р2 = 304кПа (2280мм.рт.ст.).

Задача 30. На сколько градусов надо нагреть газ, находящийся в закрытом сосуде при 0 °С, чтобы давление его увеличилось вдвое?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально температуре:

По условию задачи Т1 = 0 °С + 273 = 273К; давление возросло в два раза: Р2 = 2Р1.

Подставляя эти значения в уравнение, находим:

Ответ: Газ нужно нагреть на 2730С.

Задача 31.
При 27°С и давлении 720 мм.рт. ст. объем газа равен 5л. Кой объем займет это же количество газа при 39°С и давлении 104кПа?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 5л; Т = 298К (273 + 25 = 298); Р = 720 мм.рт.ст. (5,99 кПа); Р0 = 104 кПа; Т = 312К (273 + 39 = 312); Т = 273К. Подставляя данные задачи в уравнение, получим:

Ответ: V0 = 4,8л

Задача 32.
При 7°С давление газа в закрытом сосуде равно 96,0 кПа. Каким станет давление, если охладить сосуд до —33 °С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 96,0 кПа; Т1 = 280К (273 + 7 = 280); Т2 = 240К (273 – 33 = 240). Подставляя эти значения в уравнение, получим:

Ответ: Р2 = 82,3кПа.

Задача 33.
При нормальных условиях 1г воздуха занимает объем 773 мл. Какой объем займет та же масса воздуха при 0 °С и )и давлении, равном 93,3 кПа (700мм. рт. ст.)?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V0 = 773мл; Т0 = 298К (273 + 25 = 298); Т = 273К; Р = 93,3кПа. Подставляя данные задачи и преобразуя уравнение, получим:

Ответ: V = 769, 07 мл.

Задача 34.
Давление газа в закрытом сосуде при 12°С равно 100 кПа (750мм рт. ст.). Каким станет давление газа, если нагреть сосуд до 30°С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 100 кПа; Т1 = 285К (273 + 12 = 285); Т2 = 303К (273 + 30 = 303). Подставляя эти значения в уравнение, получим:

Ответ: Р2 = 106,3кПа.

Задача 35.
В стальном баллоне вместимостью 12л находится при 0°С кислород под давлением 15,2 МПа. Какой объем кислорода, находящегося при нормальных условиях можно получить из такого баллона?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 12л; Т = 273К (273 + 0 = 2273); Р =15,2МПа); Р0 = 101,325кПа; Т0 = 298К (273 + 25 = 298). Подставляя данные задачи в уравнение, получим:

Ответ: V0 = 1,97м3.

Задача 36.
Температура азота, находящегося в стальном баллоне под давлением 12,5 МПа, равна 17°С. Предельное давление для баллона 20,3МПа. При какой температуре давление азота достигнет предельного значения?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 12,5МПа; Т1 = 290К (273 + 17 = 290); Р2 = 20,3МПа. Подставляя эти значения в уравнение, получим:

Ответ: Т2 = 1980С.

Задача 37.
При давлении 98,7кПа и температуре 91°С некоторое количество газа занимает объем 680 мл. Найти объем газа при нормальных условиях.
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V = 680мл; Т0 = 298К (273 + 25 = 298); Т = 364К (273 + 91 = 364); Р = 98,7кПа. Подставляя данные задачи и преобразуя уравнение, получим:

Ответ: V0 = 542,3мл.

Задача 38.
При взаимодействии 1,28г металла с водой выделилось 380 мл водорода, измеренного при 21°С и давлении 104,5кПа (784мм рт. ст.). Найти эквивалентную массу металла.
Решение:
Находим объём выделившегося водорода при нормальных условиях, используя уравнение:

где Р и V – давление и объём газа при температуре Т = 294К (273 +21 = 294); Р0 = 101,325кПа; Т0 = 273К; Р = 104,5кПа. Подставляя данные задачи в уравнение,

получим:

Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200 мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:

Ответ: mЭ(Ме) = 39,4г/моль.

Задача 39.
Как следует изменить условия, чтобы увеличение массы данного газа не привело к возрастанию его объема: а) понизить температуру; б) увеличить давление; в) нельзя подобрать условий?
Решение:
Для характеристики газа количеством вещества (n, моль) применяется уравнение РV = nRT, или – это уравнение Клапейрона-Менделеева. Оно связывает массу (m, кг); температуру (Т, К); давление (Р, Па) и объём (V, м3) газа с молярной массой (М, кг/моль).

Тогда из уравнения Клапейрона-Менделеева объём газа можно рассчитать по выражению:

Отсюда следует, что V = const, если при увеличении массы (m) газа на некоторую величину будет соответственно уменьшена температура (T) системы на некоторое необходимое значение. Объём системы также не изменится при постоянной температуре, если при увеличении массы (m) газа на некоторую величину будет соответственно увеличено давление (P) системы на необходимую величину.

Таким образом, при увеличении массы газа объём системы не изменится, если понизить температуру системы или же увеличить давление в ней на некоторую величину.

Ответ: а); б).

Задача 40.
Какие значения температуры и давления соответствуют нормальным условиям для газов: а) t = 25 °С, Р = 760 мм. рт. ст.; б) t = 0 °С, Р = 1,013 • 105Па; в) t = 0°С, Р = 760 мм. рт. ст.?
Решение:
Состояние газа характеризуется температурой, давлением и объёмом. Если температура газа равна 0 °С (273К), а давление составляет 101325 Па (1,013 • 105) или 760 мм. рт. ст., то условия, при которых находится газ, принято считать нормальными.

Ответ: б); в).

Источник