В один из двух одинаковых цилиндрических сообщающихся сосудов

Автор
Тема: Жидкости и газы из сборника задач Савченко Н.Е. (Прочитано 44983 раз)
0 Пользователей и 1 Гость просматривают эту тему.
361. В цилиндрических сообщающихся сосудах находится ртуть. Отношение диаметров сосудов n = d1/d2 = 0,25. В узкий сосуд наливают воду; высота столба воды h = 80 см. На сколько опустится уровень ртути в узком сосуде и на сколько он поднимется в широком? Плотность воды ρ1 = 1,0⋅103 кг/м3, ртути ρ2 = 13,6⋅103 кг/м3.
Решение. Для сообщающихся сосудов выполняются условие равновесия жидкости (в однородной жидкости на одном уровне гидростатические давления равны) (рис. 1):
рА = рВ,
где pА = ρ2⋅g⋅h2, pВ = ρ1⋅g⋅h. Тогда
ρ2⋅g⋅h2 = ρ1⋅g⋅h или ρ1⋅h = ρ2⋅h2. (1)
Из рисунка 1 видно, что
h2 = Δh1 + Δh2, (2)
где Δh1 — высота, на которую опустится ртуть в узком сосуде, Δh2 — высота, на которую поднимется ртуть в широком сосуде.
Из условия не сжимаемости воды
ΔV1 = ΔV2, S1⋅Δh1 = S2⋅Δh2,
где [ S_{1} = frac{pi cdot d_{1}^{2} }{4}, ; ; ; S_{2} =frac{pi cdot d_{2}^{2} }{4} ] — площади поперечного сечения сосудов, d1/d2 = n — по условию. Тогда
[ frac{pi cdot d_{1}^{2} }{4} cdot Delta h_{1} =frac{pi cdot d_{2}^{2} }{4} cdot Delta h_{2}, ; ; ; Delta h_{2} =Delta h_{1} cdot left(frac{d_{1} }{d_{2} } right)^{2} =n^{2} cdot Delta h_{1}.
]
После подстановки в уравнение (2) получаем:
h2 = Δh1 + n2⋅Δh1 = Δh1⋅(1 + n2).
Подставим в уравнение (1)
[ rho _{1} cdot h=rho _{2} cdot Delta h_{1} cdot left(1+n^{2} right), ; ; ; Delta h_{1} =frac{rho _{1} cdot h}{rho _{2} cdot left(1+n^{2} right)}, ; ; ; Delta h_{2} =frac{rho _{1} cdot h cdot n^{2} }{rho _{2} cdot left(1+n^{2} right)}, ]
Δh1 = 5,5⋅10–2 м, Δh2 = 3,5⋅10–3 м.
Записан
362. В сообщающиеся сосуды налита ртуть, поверх которой в один из сосудов налита вода. Разность уровней ртути Δh = 20 мм. Плотность ртути ρ1 = 13,6⋅103 кг/м3, воды ρ2 = 1,0⋅103 кг/м3. Найти высоту столба воды.
Решение. Для сообщающихся сосудов выполняются условие равновесия жидкости (в однородной жидкости на одном уровне гидростатические давления равны) (рис. 1):
рА = рВ,
где pА = ρ1⋅g⋅Δh, pВ = ρ2⋅g⋅h2. Тогда
ρ1⋅g⋅Δh = ρ2⋅g⋅h2 или ρ1⋅Δh = ρ2⋅h2,
[ h_{2} =frac{rho _{1} cdot Delta h}{rho _{2}}, ]
h2 = 0,27 м.
Записан
363. В двух сообщающихся цилиндрических сосудах с одинаковыми поперечными сечениями площадью S = 1⋅10–2 м2 находится ртуть. В одни из сосудов поверх ртути наливают воду массой m1 = 20 кг и опускают в нее плавать груз массой m2 = 7,2 кг. На сколько поднимется уровень ртути во втором сосуде? Плотность ртути ρ = 13,6⋅103 кг/м3.
Решение. Для сообщающихся сосудов выполняются условие равновесия жидкости (в однородной жидкости на одном уровне гидростатические давления равны) (рис. 1):
рА = рВ,
где pА = ρ⋅g⋅h. Давление в точке В можно найти разными способами.
1 способ. Давление pВ = ρ1⋅g⋅h3, где ρ1 — плотность воды, h3 = h1 + h2, h1 — высота столбца воды массой m1, h2 — высота столбца воды, вытесненная при погружении в воду тела массой m2 и т.п.
2 способ. Так как тело плавает в воде, то давление воды и плавающего тела в точке В
[ p_{B} = frac{left(m_{1} +m_{2} right)cdot g}{S}. ]
Тогда
[ rho cdot g cdot h=frac{left(m_{1} +m_{2} right)cdot g}{S}, ;; ; rho cdot h=frac{m_{1} +m_{2} }{S}.;;; (1) ]
Из рисунка 1 видно, что
h = Δh1 + Δh2,
где Δh1 — высота, на которую поднимется ртуть, Δh2 — высота, на которую ртуть опустится.
Из условия не сжимаемости воды
ΔV1 = ΔV2, S⋅Δh1 = S⋅Δh2, Δh1 = Δh2.
В итоге получаем, с учетом уравнения (1):
[ h=2Delta h_{1} =frac{m_{1} +m_{2} }{Scdot rho }, ; ; ; Delta h_{1} =frac{m_{1} +m_{2} }{2Scdot rho }, ]
Δh1 = 0,1 м.
Записан
364. Шарик массой m = 40 г плавает в одном из двух одинаковых цилиндрических сообщающихся сосудов, заполненных водой (рис. 1). Площадь поперечного сечения каждого сосуда S = 20 см2. На сколько изменится уровень воды, если вынуть шарик? Плотность воды ρ = 1,0 г/см3.
Решение. На шарик действуют силы тяжести (m⋅g) и архимедова сила (FA). Запишем условие плавания тела:
FA = m⋅g,
где FA = ρ⋅g⋅Vn, Vn — объем части шарика, погруженного в воду. Тогда
ρ⋅g⋅Vn = m⋅g или ρ⋅Vn = m.
Если шарик вынуть из воды, то объем воды уменьшиться на Vn. Так как вода занимается два сообщающихся сосуда площадью S каждый, то уровень воды (высота столбца) уменьшиться на
[ Delta h=frac{V_n}{2S}=frac{m}{2rho cdot S}, ]
Δh = 1⋅10–2 м.
Записан
365. Два цилиндрических сосуда соединены у дна тонкой трубкой с краном (рис. 1). Один сосуд имеет площадь поперечного сечения S1 = 15 см2, второй — S2 = 5,0 см2. Сосуды заполнены водой: первый до высоты h1 = 20 см, второй до высоты h2 = 40 см. Каков будет уровень воды в сосудах, если открыть кран К в соединительной трубке?
Решение. Так как давление на дно сосуда больше в правом сосуде, то после открытия кран К вода будет перетекать с правого сосуда в левый. Пусть высота столбца жидкости в сосудах станет равной h3, уровень воды в сосуде площадью S1 увеличится на Δh1, в сосуде площадью S2 уменьшится на Δh2 (рис. 2). Из рисунка видно, что
Δh1 = h3 – h1, (1)
Δh2 = h2 – h3. (2)
Из условия не сжимаемости воды
ΔV1 = ΔV2, S1⋅Δh1 = S2⋅Δh2. (3)
Решим систему уравнений (1)-(3). Например,
S1⋅(h3 – h1) = S2⋅(h2 – h3), h3⋅(S1 + S2) = S1⋅h1 + S2⋅h2,
[ h_{3} =frac{S_{1} cdot h_{1} +S_{2} cdot h_{2} }{S_{1} +S_{2}}, ]
h3 = 0,25 м.
« Последнее редактирование: 13 Декабря 2011, 19:00 от alsak »
Записан
366. Деталь отлита из сплава железа и никеля. Определить, сколько процентов по объему составляют железо и никель, а также объем всей детали, если в воздухе деталь весит Р1 = 33,52 Н, а в воде — Р2 = 29,60 Н. Плотность железа ρ1 = 7,9⋅103 кг/м3, никеля ρ2 = 8,9⋅103 кг/м3, воды ρ3 = 1,0⋅103 кг/м3. Архимедову силу в воздухе не учитывать.
Решение. Будем считать, что вес детали определяют при помощи динамометра. Тогда вес детали — это сила упругости пружины динамометра.
В воздухе на деталь, подвешенной к динамометру, действует сила тяжести ((m1 + m2)⋅g) и сила упругости (Fy1) (архимедову силу в воздухе не учитывать) (рис. 1). Из проекции второго закона Ньютона получаем:
P1 = Fy1 = (m1 + m2)⋅g,
где m1 = ρ1⋅V1 — масса железа в детали, V1 — объем железа, m2 = ρ2⋅V2 — масса никеля в детали, V2 — объем никеля. Тогда
P1 = (ρ1⋅V1 + ρ2⋅V2)⋅g. (1)
В воде на деталь, подвешенной к динамометру, действует сила тяжести ((m1 + m2)⋅g), сила упругости (Fy2) и архимедова сила (FA) (рис. 2). Из проекции второго закона Ньютона получаем:
P2 = Fy2 = (m1 + m2)⋅g – FA,
где FA = ρ3⋅g⋅V, V = V1 + V2 — объем всей детали. Тогда
P2 = (ρ1⋅V1 + ρ2⋅V2)⋅g – ρ3⋅g⋅(V1 + V2). (2)
Решим систему уравнений (1)-(2) и найдем V1, V2 и V. Например,
[ P_{2} =P_{1} -rho _{3} cdot gcdot left(V_{1} +V_{2} right), ; ; ; V=V_{1} +V_{2} =frac{P_{1} -P_{2} }{rho _{3} cdot g}, ]
V = 4⋅10–4 м3.
V2 = V – V1, P1 = (ρ1⋅V1 + ρ2⋅(V – V1))⋅g,
(ρ1 – ρ2)⋅V1⋅g = P1 – ρ2⋅V⋅g,
[ V_{1} =frac{P_{1} }{left(rho _{1} -rho _{2} right)cdot g} -frac{rho _{2} cdot V}{rho _{1} -rho _{2} }, ; ; ; frac{V_{1} }{V} =frac{P_{1} }{left(rho _{1} -rho _{2} right)cdot g} cdot frac{1}{V} -frac{rho _{2} }{rho _{1} -rho _{2} } = ]
[ =frac{P_{1} }{left(rho _{1} -rho _{2} right)cdot g} cdot frac{rho _{3} cdot g}{P_{1} -P_{2} } -frac{rho _{2} }{rho _{1} -rho _{2} } =left(frac{P_{1} cdot rho _{3} }{P_{1} -P_{2} } -rho _{2} right)cdot frac{1}{rho _{1} -rho _{2}}, ]
V1/V = 0,35 (35%), V2/V = 1 – 0,35 = 0,65 (65%).
Записан
367. Браслет массой М = 80 г сделан из сплава золота и серебра. Вычислить массу золота, содержащегося в браслете, располагая следующими данными: плотность золота ρ1 = 19,3 г/см3, плотность серебра ρ2 = 10,5 г/см3; при погружении браслета в воду, находящуюся в сосуде с вертикальными стенками и площадью основания S = 25 см2, уровень воды поднимается на h = 2,0 мм.
Решение. Масса браслета равна
M = m1 + m2,
где m1 = ρ1⋅V1 — масса золота в браслете, V1 — объем золота, m2 = ρ2⋅V2 — масса серебра в браслете, V2 — объем серебра. Тогда
M = ρ1⋅V1 + ρ2⋅V2. (1)
При погружении в воду браслет вытесняет объем воды, равный объему тела, т.е.
V = S⋅h = V1 + V2. (2)
Решим систему уравнений (1)-(2). Например,
V2 = S⋅h – V1, M = ρ1⋅V1 + ρ2⋅(S⋅h – V1),
(ρ1 – ρ2)⋅V1 = M – ρ2⋅S⋅h,
[ V_{1} =frac{M-rho _{2} cdot Scdot h}{rho _{1} -rho _{2}}, ; ; ; m_{1} =rho _{1} cdot V_{1} =rho _{1} cdot frac{M-rho _{2} cdot Scdot h}{rho _{1} -rho _{2}}, ]
m1 = 6,0⋅10–2 кг.
Записан
368. Согласно желанию сиракузского властителя, Архимед должен был определить содержание золота в короне, состоящей из золотых и серебряных частей, не разрушая ее. Для этого Архимед взвесил корону в воздухе и получил вес P1 = 25,4 Н, а затем в воде, получив вес Р2 = 23,4 Н. Зная плотность золота, серебра и воды (соответственно ρ1 = 19,3 г/см3, ρ2 = 10,5 г/см3 и ρ3 = 1,00 г/см3), определить, как и Архимед, массу золота, содержащегося в этой короне. Ускорение свободного падения считать равным g = 10,0 м/с2.
Решение. Будем считать, что вес короны определяли при помощи динамометра. Тогда вес короны — это сила упругости пружины динамометра.
В воздухе на корону, подвешенной к динамометру, действует сила тяжести ((m1 + m2)⋅g) и сила упругости (Fy1) (архимедову силу в воздухе не учитывать) (рис. 1). Из проекции второго закона Ньютона получаем:
P1 = Fy1 = (m1 + m2)⋅g,
где m1 = ρ1⋅V1 — масса золота в короне, V1 — объем золота, m2 = ρ2⋅V2 — масса серебра в детали, V2 — объем серебра. Тогда
P1 = (ρ1⋅V1 + ρ2⋅V2)⋅g. (1)
В воде на корону, подвешенной к динамометру, действует сила тяжести ((m1 + m2)⋅g), сила упругости (Fy2) и архимедова сила (FA) (рис. 2). Из проекции второго закона Ньютона получаем:
P2 = Fy2 = (m1 + m2)⋅g – FA,
где FA = ρ3⋅g⋅V, V = V1 + V2 — объем всей короны. Тогда
P2 = (ρ1⋅V1 + ρ2⋅V2)⋅g – ρ3⋅g⋅(V1 + V2). (2)
Решим систему уравнений (1)-(2), найдем V1 и m1. Например,
[ P_{2} =P_{1} -rho _{3} cdot gcdot left(V_{1} +V_{2} right), ; ; ; V=V_{1} +V_{2} =frac{P_{1} -P_{2} }{rho _{3} cdot g}, ]
V2 = V – V1, P1 = (ρ1⋅V1 + ρ2⋅(V – V1))⋅g,
(ρ1 – ρ2)⋅V1⋅g = P1 – ρ2⋅V⋅g,
[ V_{1} =frac{P_{1} -rho _{2} cdot Vcdot g}{left(rho _{1} -rho _{2} right)cdot g} =frac{rho _{3} cdot P_{1} -rho _{2} cdot left(P_{1} -P_{2} right)}{left(rho _{1} -rho _{2} right)cdot rho _{3} cdot g}, ; ; ; m_{1} =rho _{1} cdot V_{1} =rho _{1} cdot frac{rho _{3} cdot P_{1} -rho _{2} cdot left(P_{1} -P_{2} right)}{left(rho _{1} -rho _{2} right)cdot rho _{3} cdot g} , ]
m1 = 0,965 кг.
Записан
369. В цилиндрическом сосуде с не смешивающейся с водой жидкостью, плотность которой ρ = 1,2 г/см3, при температуре t = 0 °С плавает льдинка массой m = 1 кг. На сколько изменится уровень этой жидкости в сосуде, когда льдинка растает? Площадь основания сосуда S = 0,1 м2.
Решение. После того как льдинка растаяла, объем жидкости в сосуде увеличился на объем воды V, полученной из льдинки. Но плотность воды меньше плотности жидкости, поэтому вся вода окажется сверху, и уровень жидкости опустится до первоначальной высоты h.
1 способ. Объем вытесненной жидкости
[V_{vt} =V_{1} +V_{2} =frac{mcdot g}{rho cdot g} =frac{m}{rho } =S_{1} cdot left(h_{1} +h_{2} right).]
Объем жидкости, которая поднялась — это
[V_{1} =left(S-S_{1} right)cdot h_{2} =S_{1} cdot h_{1} .]
Из второго уравнения получаем
[S_{1} cdot left(h_{1} +h_{2} right)=Scdot h_{2} .]
И тогда
[S_{1} cdot left(h_{1} +h_{2} right)=Scdot h_{2} =frac{m}{rho } ,; ; h_{2} =frac{m}{Scdot rho } .]
2 способ. Изменение давления на дно сосуда равно
[Delta p=frac{mcdot g}{S} =rho cdot gcdot Delta h,; ; Delta h=h_{2} =frac{m}{rho cdot S} .]
Ответ. Уровень жидкости опустится на h2 = 8,3⋅10–3 м.
« Последнее редактирование: 21 Августа 2019, 17:27 от alsak »
Записан
370. Теплоход, войдя в гавань, выгрузил часть груза; при этом его осадка уменьшилась на h = 0,6 м. Найти массу груза, оставленного теплоходом в гавани, если площадь поперечного сечения теплохода на уровне ватерлинии S = 5400 м2. Плотность воды ρ = 1⋅103 кг/м3.
Решение. На теплоход с грузом действуют сила тяжести теплохода (m1⋅g), архимедова сила (FA1) и вес груза (m2⋅g) (рис. 1, а). Тело неподвижно, поэтому уравнение второго закона Ньютона в проекции на вертикальную ось имеет вид:
FA1 – m1⋅g – m2⋅g = 0,
где FA1 = ρ⋅g⋅V1, V1 = S⋅h1, h1 — глубина погружения теплохода с грузом. Тогда
ρ⋅g⋅S⋅h1 – m1⋅g – m2⋅g = 0. (1)
На теплоход без груза действуют сила тяжести теплохода (m1⋅g), архимедова сила (FA2) (рис. 1, б). В проекции на вертикальную ось получаем:
FA2 – m1⋅g = 0,
где FA2 = ρ⋅g⋅V2, V2 = S⋅h2, h2 — глубина погружения теплохода без груза, h2 = h1 – h. Тогда
ρ⋅g⋅S⋅(h1 – h) – m1⋅g = 0. (2)
Решим систему уравнений (1)-(2). Например,
ρ⋅g⋅S⋅h1 – m1⋅g = m2⋅g, ρ⋅g⋅S⋅h1 – m1⋅g – ρ⋅g⋅S⋅h = 0,
m2⋅g = ρ⋅g⋅S⋅h, m2 = ρ⋅S⋅h,
m2 = 3,2⋅106 кг.
Записан
Источник
504. Сосуд с жидкостью наклонили (рис. 131). Одинаковое ли давление оказывает после этого жид¬кость на боковые стенки А и В в точках, лежащих на одном горизонтальном уровне?
Жидкость оказывает одинаковое давление на одном горизонтальном уровне везде, в том числе и на стенках А и В (см. рис. 131).
505. Сосуд с водой имеет форму, изображенную на рисунке 132. Одинаково ли давление воды на боковые стенки сосуда на уровне аб?
На уровне ab давление воды на боковые стенки одно и то же (см. рис. 132).
506. Цилиндрические сосуды уравновешены на весах (рис. 133). Нарушится ли равновесие весов, если в них налить воды столько, что поверхность ее установится на одинаковом уровне от дна сосудов? Одинаково ли будет давление на дно сосудов?
Равновесие весов нарушается, так как в разных сосудах различная масса воды. Давление на дно сосуда будет одинаковым, так как высота столба воды в обоих сосудах одна и та же (см. рис. 133)
507. Цилиндрические сосуды уравновешены на весах (см. рис. 133). Мальчик налил в оба сосуда воду одинаковой массы. Нарушилось ли равновесие весов? Одинаково ли будет давление воды на дно сосудов?
Равновесие весов не нарушилось. Давление воды на дно сосуда будет различным, так как уровень налитой воды будет различным (см. рис. 133).
508. В цилиндрический сосуд, частично заполненный водой, опустили деревянный брусок. Изменилось ли давление воды на дно сосуда?
Давление воды на дно увеличилось, так как при опускании в воду деревянного бруска ее уровень поднялся.
509. В трех сосудах с одинаковой площадью дна налита вода до одного уровня (рис. 134). В каком сосуде налито больше воды? Одинаково ли давление на дно в этих сосудах? Почему?
Воды налито больше в крайнем левом сосуде. Давление на дно будет одинаковым во всех трех сосудах, так как везде вода налита до одного уровня (см. рис. 134).
510. Уровень воды в сосудах одинаковый (рис. 135). Будет ли переливаться вода из одного сосуда в другой, если открыть кран?
При открывании крана вода из одного сосуда в другой переливаться не будет, так как уровень воды в сосудах будет одинаковый, а следовательно давление воды на любом уровне так же одинаково (см. рис. 135).
511. Уровень жидкостей в сосудах (см. рис. 135) одинаковый. В левом налита вода, в правом — керосин. Одинаковы ли давления на дно? Одинаковы ли давления на кран? Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран?
Давление воды на дно и на кран больше, чем давление керосина. Объясняется это тем, что плотность воды больше плотности керосина. Если кран открыть, то вследствие разности давлений вода потечет в сосуд с керосином (см. рис. 135).
512. В левой части сосуда над жидкостью находится воздух (рис. 136). Какую высоту столба жидкости следует учитывать при расчете давления на дно сосуда: высоту Н или высоту H1? Ответ объясните.

513. В полиэтиленовый мешок налита вода (рис. 137). Что показывают динамометры: давление или силы, действующие на столики динамометров? Стрелка правого динамометра закрыта листом бумаги. Каково показание правого динамометра? Будут ли изменяться показания динамометров, если воду в мешок доливать (выливать)? Ответы обоснуйте.
Динамометры показывают силы давления жидкости на боковые стенки сосуда с водой. Показания их одинаковы и равны 70Н. Если воду в мешок доливать, то показания динамометров увеличатся, а если воду выливать, то уменьшатся, т.к. увеличится либо уменьшится давление столба жидкости (см. рис.137).
514. Одинаково ли давление воды на дно сосудов (рис. 138)? Чему равно это давление? Изменится ли давление, если воду заменить керосином? Чему оно будет равно в этом случае?

515. Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, налитая до того же уровня?
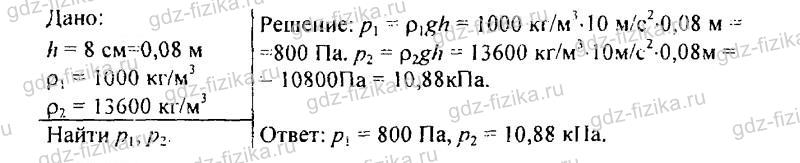
516. Какое давление на дно сосуда оказывает слой керосина высотой 0,5 м?

517. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда.
518. Сосуды с водой имеют равные площади дна (рис. 139). В каком из них избыточное давление воды на дно (без учета атмосферного давления) больше и во сколько раз?

519. Водолаз в жестком скафандре может погружаться в море на глубину 250 м, искусный ныряльщик — на глубину 20 м. На сколько и во сколько раз отличаются давления воды на этих глубинах?
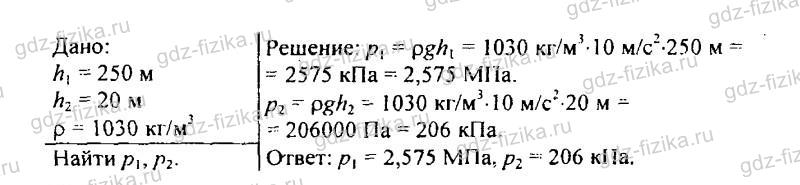
520. Рассчитайте давление воды: а) на самой большой глубине Тихого океана — 11 035 м; б) на наибольшей глубине Азовского моря — 14 м (плотность воды в нем принять равной 1020 кг/м3).
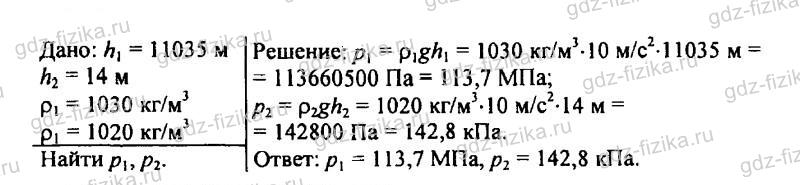
521. Определите по графику (рис. 140) глубину погружения тела в озеро, соответствующую давлению воды 100, 300 и 500 кПа.
10 м; 30 м; 50 м (рис. 140).
522. Аквариум наполнен доверху водой. С какой силой давит вода на стенку аквариума длиной 50 см и высотой 30 см?
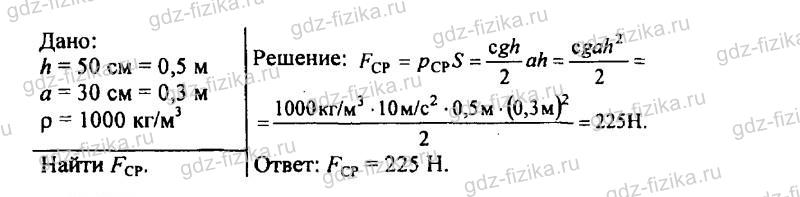
523. В аквариум высотой 32 см, длиной 50 см и шириной 20 см налита вода, уровень которой ниже края на 2 см. Рассчитайте: а) давление воды на дно; б) вес воды; в) силу, с которой вода действует на стенку шириной 20 см.
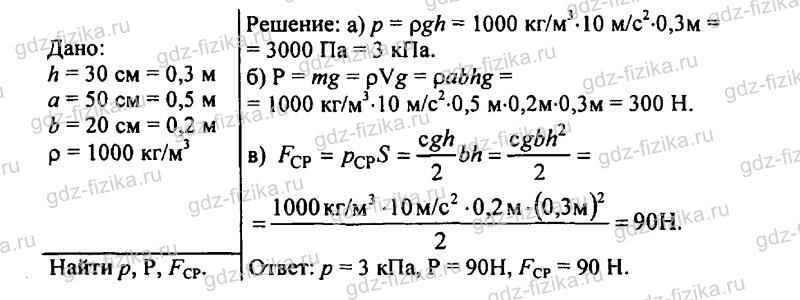
524. Ширина шлюза 10 м. Шлюз заполнен водой на глубину 5 м. С какой силой давит вода на ворота шлюза?
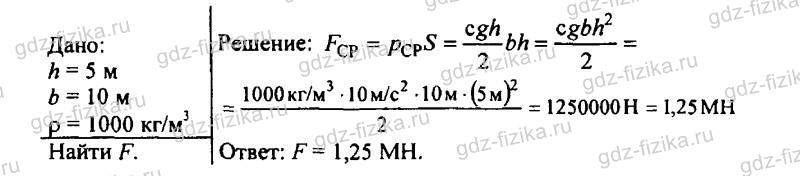
525. В цистерне, заполненной нефтью, на глубине 3 м имеется кран, площадь отверстия которого 30 см2. С какой силой давит нефть на кран?

526. Прямоугольный сосуд вместимостью 2 л наполовину наполнен водой, а наполовину керосином, а) Каково давление жидкостей на дно сосуда? б) Чему равен вес жидкостей в сосуде? Дно сосуда имеет форму квадрата сo стороной 10 см.

527. Определите силу, с которой действует керосин на квадратную пробку площадью поперечного сечения 16 см2, если расстояние от пробей до уровня керосина в сосуде равно 400 мм (рис. 141).

528. Какую силу испытывает каждый квадратный метр площади поверхности водолазного костюма при погружении в морскую воду на глубину 10 м?
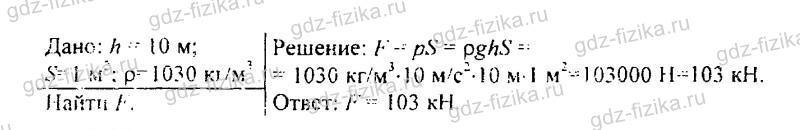
529. Плоскодонная баржа получила пробоину в дне площадью 200 см2. С какой силой нужно давить на пластырь, которым закрывают отверстие, чтобы сдержать напор воды на глубине 1,8 м? (Вес пластыря не учитывать.)
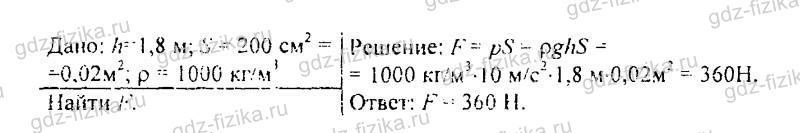
530. Определите высоту уровня воды в водонапорной башне, если манометр, установленный у ее основания, показывает давление 220000 Па.
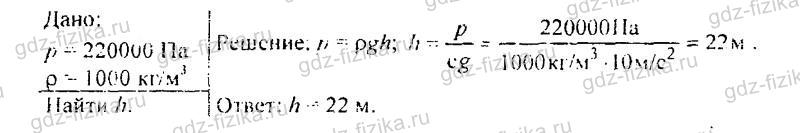
531. На какой глубине давление воды в море равно 412 кПа?
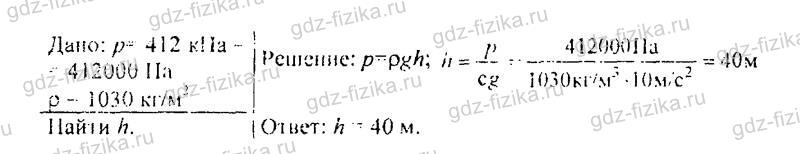
532. Напор воды в водокачке создается насосом. Определите на какую высоту поднимается вода, если давление, созданное насосом, равно 400 кПа?
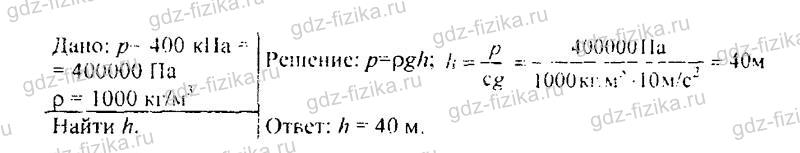
533. Брусок размером 0,5×0,4×0,1 м находится в баке с водой на глубине 0,6 м (рис. 142). Вычислите: а) с какой силой вода давит на верхнюю грань бруска; б) на нижнюю грань бруска; в) сколько весит вода, вытесненная бруском.
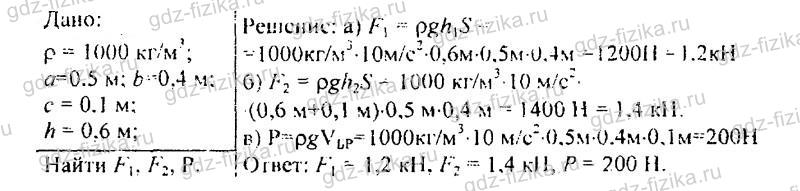
534. Произведите расчет, взяв данные предыдущей задачи, предполагая, что воду заменили керосином.
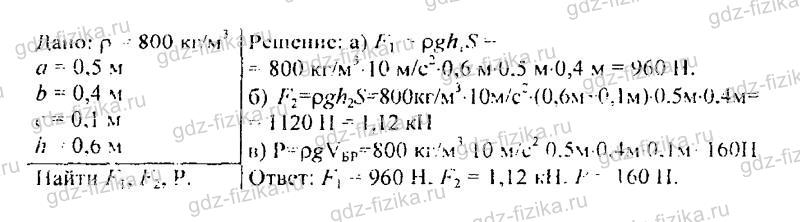
535. Используя результаты двух предыдущих задач, вычислите, на сколько сила, действующая на тело снизу, больше силы, действующей на тело сверху: а) в воде; б) в керосине. Сравните полученные результаты с весом вытесненной воды и с весом вытесненного керосина.

536. Один из кофейников, изображенных на рисунке 143, вмещает больше жидкости, чем другой. Укажите какой и объясните.
Правый кофейник вмещает больше жидкости, чем левый, гак как у него кончик носика находится выше.
537. Точкой А обозначен уровень воды в левом колене трубки (рис. 144). Сделайте рисунок и на нем отметьте точкой В уровень воды в правом колене трубки.

538. В сообщающиеся сосуды налита вода. Что произойдет и почему, если в левый сосуд долить немного воды (рис. 145); в средний сосуд долить воды (рис. 146)?
Уровень воды увеличится во всех сосудах на одинаковую высоту. Таким образом, уровни снова выравнятся (рис. 145, 146).
539. Справедлив ли закон сообщающихся сосудов в условиях невесомости? Объясните почему.
Закон сообщающихся сосудов в условиях невесомости не действует, так как жидкости в состоянии невесомости не обладают весом и потому не оказывают давления на дно сосудов.
540. Как при помощи сообщающихся сосудов проверить, горизонтально ли нанесена филенка (линия, отделяющая окраску панели от верхней части стены)?
Нужно взять длинную тонкую резиновую трубку, вставить стеклянные трубки на концах, залить эту систему водой, а концы стеклянных трубок подвести к филенке. Используя свойство сообщающихся сосудов, пройтись с одной из стеклянных трубок вдоль стены.
541. Объясните действие фонтана (рис. 147).
Действие фонтана объясняется тем, что давление жидкости в верхнем конце правой трубки будет больше атмосферного, так как уровень воды в этой трубке меньше уровня воды в левой трубке.
542. В левом колене сообщающихся сосудов налита вода, в правом — керосин (рис. 148). Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
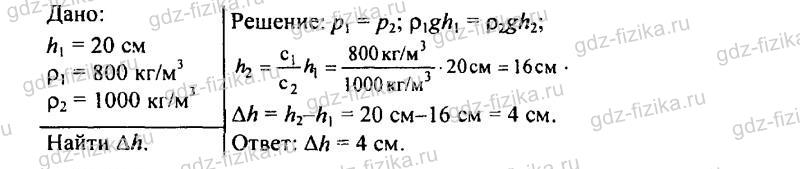
543. В сообщающихся сосудах находятся ртуть и вода (рис. 149). Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?

544. В сообщающихся сосудах находилась ртуть. Когда в правую трубку налили слой керосина высотой 34 см, то уровень ртути в левой трубке поднялся на 2 см. Какой высоты следует налить слой воды в левую трубку, чтобы ртуть в трубках установилась на одинаковом уровне (рис. 149)?
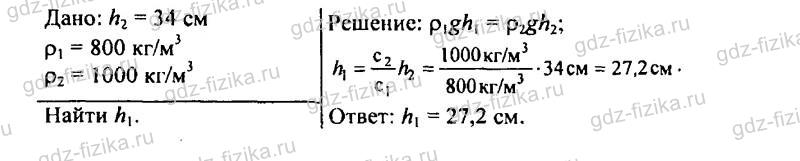
545. В сообщающихся сосудах находятся ртуть, вода и керосин (рис. 150). Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?

Источник