В одном сосуде объемом v находится v молей газа
При работе со своими учениками, у меня накапливается много задач. Поэтому я публикую разборы задач в свободный доступ, стараюсь делать это максимально подробно и понятно, чтобы начинающие могли прочитать и разобраться в нужной для них теме. Ну а за подробными индивидуальными консультациями и репетиторством вы можете написать в мою группу в вк или в личные сообщения. Также большое количество разборов задач вы сможете найти в моей группе Репетитор IT mentor
Задача 1. На тело массой 100 кг, лежащее на наклонной плоскости, которая образует с горизонтом угол 40°, действует горизонтальная сила 1500 Н. Определить:
1) силу, прижимающую тело к плоскости;
2) силу трения тела о плоскость;
3) ускорение, с которым поднимается тело. Коэффициент трения k = 0.10; g = 10м/с².
Задача 2. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Найти ускорение тела, если на него действует сила тяжести P, а коэффициент трения между телом и плоскостью равен k . При какой величине силы F движение будет равномерным.
Задача 3. Два шара массами m1 = 2.5 кг и m2 = 1.5 кг движутся навстречу друг другу со скоростями v1 = 6 м/c и v2 = 2 м/c . Определить: 1) скорости шаров после удара; 2) кинетические энергии шаров до и после удара; 3)энергию, затраченную на деформацию шаров при ударе. Удар считать прямым, неупругим.
Прикрепляю очередной разбор задачи по физике по теме закона сохранения импульса. Неупругие шары после удара не восстанавливают свою первоначальную форму. Таким образом, сил, которые отталкивали бы шары друг от друга, не возникает. Это значит, что после удара шары будут двигаться вместе (слипшись) с одной и той же скоростью . Эту скорость определим по закону сохранения импульса. Так как шары двигаются по одной прямой, то можно записать импульс системы до удара и после удара. Считаем, что в задаче не действует диссипативных сил (сил трения, сопротивления воздуха и т.д.), поэтому импульс вдоль оси Ox сохраняется, тогда (смотри решение на картинке). Расписал довольно подробно, но если что-то не будет понятно, то задавайте вопросы в комментариях.
Задача 4. Диск массой m, радиус которого R , вращается с угловой скоростью ω0 вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. После прекращения действия на него силы диск останавливается в течение времени t. Определить угловое ускорение диска и тормозящий момент, действующий на него.
Задача 5. Два тела массами m1 и m2 связаны нитью, перекинутой через блок массой M . Найти ускорение тел, считая блок сплошным диском.
Задача 6. Шар катится по горизонтальной поверхности со скоростью v . На какую высоту h относительно своего первоначального положения поднимется шар, если он начнет вкатываться на наклонную плоскость без проскальзывания?
Задача 7. На краю вращающейся с угловой скоростью ω0 платформе стоит человек массой m. После того, как человек перешёл в другую точку платформы, угловая скорость её вращения стала равной ω. Найти расстояние от оси вращения до человека, считая платформу диском массой M и радиусом R.
Задача 8. Тело массой m брошено со скоростью v0 под углом α к горизонту. Найти кинетическую и потенциальную энергию тела в высшей точке траектории.
Задача 9. На горизонтальной поверхности находятся два тела массами m1 = 10 кг и m2 =15 кг, связанные нитью. К телу массой m2 прикладывают силу F = 100 Н, направленную под углом α = 60° к горизонту. Определить ускорение грузов и силу натяжения нити, соединяющей грузы. Трением пренебречь. (обязательно указать все силы на чертеже!)
Задача 10. На поверхности стола лежит груз массой m2 = 2 кг. На нити, прикрепленной к грузу m2 и перекинутой через невесомый блок, подвешен груз m1 = 1 кг. Коэффициент трения груза о поверхность стола 0,2. Найти ускорение грузов и силу натяжения нити.
Задача 11. Лодка массой 200 кг и длиной 3 м стоит неподвижно в стоячей воде. Мальчик массой 40 кг в лодке переходит с носа на корму. Определите, на какое расстояние при этом сдвинется лодка.
Считаем, что в нашей задаче не действует внешних сил, поэтому по теореме о центре массы системы грузов, можно считать, что координаты центра масс сохраняются в проекциях на ось OX (по оси OY движения не происходит). Проведем ось Y(ноль оси X) через центр лодки, тогда можно записать координаты человека и лодки до перехода человека с носа на корму.
Задача 12. Шарик массой 5 кг подвешен на нити. Нить может выдержать максимальное натяжение 100 Н. На какой минимальный угол от положения равновесия нужно отклонить нить с шариком, чтобы он оборвал нить, проходя через положение равновесия? (обязательно сделать рисунок, указать действующие силы!)
Задача 13. Два неупругих шара массами m1=2 кг и m2=3 кг движутся со скоростями соответственно v1=8 м/c и v2=4м/с. Определить количество теплоты, выделившееся при их столкновении. Рассмотреть 2 случая: 1) шары движутся навстречу друг другу; 2) меньший шар догоняет больший.
Задача 14. Тело совершает гармонические колебания по закону x(t) = 50⋅sin(π/3⋅t) (см). Определить полную энергию тела, если его масса 0,2 кг. Какая сила действует на тело в момент времени t = 0,5 с?
Задача 15. Два математических маятника, длины которых отличаются на Δℓ =16 см, совершают за одно и то же время: один − 10 колебаний, другой − 6 колебаний. Определить длины маятников.
Задача 16. Определить, сколько молей и молекул водорода содержится в объёме V = 5 м³ под давлением Р = 767 мм.рт.ст. при температуре t = 18 ° С. Какова плотность газа?
Задача 17. Сколько кислорода выпустили из баллона ёмкостью 1 дм3, если давление его изменилось от 14 атм до 7 атм, а температура от 27°С до 7 °С ?
Задача 18. В сосуде объёмом V = 2 м³ находится смесь m1 = 4 кг гелия и m2 = 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
Задача 19. В сосуде содержится смесь газов: гелия массой 12 г и водорода массой 2 г, температура в сосуде 77°С, давление 20 кПа. Определить молярную массу и плотность смеси газов.
Задача 20. Гелий массой 20 г нагрели от 100°С до 400°С, причем газу была передана теплота 30 кДж. Найти изменение внутренней энергии гелия и совершенную им работу.
Задача 21. При изотермическом расширении от 0,1 м3 трех молей газа его давление меняется от 4,48 атм до 1 атм. Найти совершаемую при этом работу и температуру, при которой протекает процесс.
Задача 22. Моль идеального газа, имевший первоначально температуру 300ºК, расширяется изобарически до тех пор, пока его объем не возрастет в 3 раза. Затем газ охлаждается изохорически до первоначальной температуры. Определить суммарное получаемое газом количество теплоты. Обязательно нарисовать графики процессов.
Задача 23. Азот массой m = 1 кг занимает при температуре Т1 = 300 К объём V = 0,5 м³. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определить конечный объём газа и конечную температуру.
Задача 24. Газ расширяется адиабатически, причём объём его увеличивается вдвое, а термодинамическая температура падает в 1,32 раза. Какое число степеней свободы i имеют молекулы этого газа?
Задача 25. Баллон ёмкостью V = 20 л с кислородом при давлении Р = 107 Па и температуре t1 = 70 ºС нагревается до температуры t2 = 270 ºС. Какое количество теплоты при этом поглощает газ?
Задача 26. Азот, занимающий при давлении, равном Р1 = 10⁵ Па объём V1 = 10 л, расширяется вдвое. Найти конечное давление и работу, совершённую газом в процессах: а) изобарном; б) изотермическом; в) адиабатном.
Задача 27. Кислород, масса которого 200 г, нагревают от температуры Т1 =300 К до Т2 = 400 К. Найти изменение энтропии, если известно, что начальное и конечное давление газа одинаковы и близки к атмосферному.
Задача 28. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 1,5∙10⁵ Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 260 К. Найти КПД машины, количество теплоты Q1, получаемое машиной за один цикл от нагревателя, и количество теплоты Q2, отдаваемое за один цикл холодильнику.
Задача 29. Найти суммарную кинетическую энергию Е поступательного движения всех молекул, содержащихся в объёме V = 1 дм³ газа при атмосферном давлении.
Задача 30. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 100 г водорода при температуре 400 К ? Чему равна полная внутренняя энергия газа?
Спасибо, что дочитали до конца, дорогие подписчики 🙂 Если вам интересен подобный контент и разборы задач, то оставляйте обратную связь в виде лайков и комментариев.
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в Telegram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Источник
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 2 л находится 10 г идеального газа при давлении 1 атм. и температуре 300 К. Во втором сосуде объёмом 4 л находится 20 г того же газа при давлении 2 атм. Чему равна температура газа во втором сосуде? (Ответ дайте в кельвинах.)
Уравнение состояния газа: [pV=nu RT=dfrac{m}{mu}RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа, (m) — масса газа, (mu) — молярная масса газа.
Для первого сосуда: [p_1V_1=dfrac{m_1}{mu}RT_1] Для второго сосуда: [p_2V_2=dfrac{m_2}{mu}RT_2] Поделим уравнения друг на друга: [dfrac{p_1V_1}{p_2V_2}=frac{m_1T_1}{m_2T_2}] [T_2=T_1cdotdfrac{m_1}{m_2}cdotdfrac{V_2}{V_1}cdotdfrac{p_2}{p_1}=300text{ К}cdotdfrac{1}{2}cdot2cdot2=600 text{ К}]
Ответ: 600
При уменьшении абсолютной температуры газа на 300 К давление уменьшилось в 5 раз. Какова начальная температура газа, если в ходе эксперимента количество вещества уменьшилось втрое, а объём оставался постоянным? (Ответ дайте в кельвинах.)
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния: [begin{cases}
p_1 V=nu_1 R T_1\
p_2 V=nu_2 R T_2
end{cases}] где (p_1) и (p_2) — давления газа в первом и втором состояниях, V — объём газа, (nu_1) и (nu_2)— количество вещества в первом и втором состояниях, (R) — универсальная газовая постоянная, (T_1) и (T_2) — абсолютная температура в первом и втором состояниях.
Поделив одно уравнение на другое, получим: [dfrac{p_1}{p_2} = dfrac{nu_1 T_1}{nu_2 T_2}] Так как (nu_1 = 3nu_2) и (p_1 = 5p_2), то: [dfrac{5p_2}{p_2} = dfrac{3nu_2cdot T_1}{nu_2cdot T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5=dfrac{3T_1}{T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_2 = 3T_1] Так как (T_2 = (T_1 – 200) К), то: [5(T_1 – 300text{ K}) = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_1 – 1500text{ K } = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
2T_1 = 1500text{ K }
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
T_1 = 750text{ K }]
Ответ: 750
На графиках приведены зависимости давления (p) и объема (V) от времени (t) для 1 моля идеального газа. Чему равна температура газа в момент (t) = 30 минут? (Ответ дайте в градусах Кельвина с точностью до 10 К.)
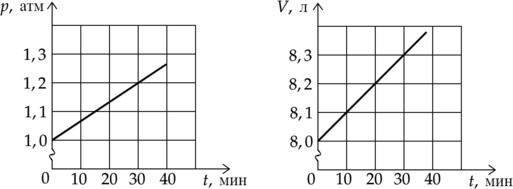
Уравнение состояния идеального газа: [displaystyle pV=nu RT,] где (p)—давление газа, (V)—объем газа, (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (T) — температура. Выразим температуру газа: [T=dfrac{pV}{nu R}] Из графика найдем давление и объем в момент времени 30 мин:
(p=1,2cdot10^5) Па
(V=8,3cdot10^{-3}text{ м$^3$})
Подставим известные и найденные значения в формулу: [T=dfrac{1,2cdot10^5text{ Па}cdot8,3cdot10^{-3}text{ м$^3$}}{1text{ моль}cdot8,31text{ }dfrac{text{Дж}}{text{моль}}} approx 120 text{ К}]
Ответ: 120
В сосуде неизменного объёма находится разреженный газ в количестве 3 моль. Во сколько раз изменится давление газа в сосуде, если выпустить из него 1 моль газа, а абсолютную температуру газа уменьшить в 2 раза?
“Демоверсия 2019”
Запишем уравнение Клапейрона – Менделеева: [p1V=nu_1RT_1=3RT_1] [p_2V=nu_2RT_2=2Rdfrac{T_1}{2}=RT_1] [dfrac{p_1}{p_2}=dfrac{3RT_1}{RT_1}=3]
Ответ: 3
В сосуде неизменного объёма находится идеальный газ. Во сколько раз нужно увеличить количество газа в сосуде, чтобы после уменьшения абсолютной температуры газа в 2 раза его давление стало вдвое больше начального?
“Досрочная волна 2020 вариант 1”
Из уравнения Клапейрона –Менделеева: [pV=nu RT] чтобы давление ((p)) увеличилось в 2 раза, при уменьшении температуры ((T)) в 2 раза, количество вещества ((nu)) должно увеличится в 4 раза
Ответ: 4
В сосуде неизменного объема находится разреженный газ в количестве 4 моль. Во сколько раз нужно увеличить абсолютную температуру газа, чтобы после удаления из сосуда 3 моль газа, давление осталось неизменным?
“Основная волна 2020 ”
Уравнение Клайперона – Менделеева: [pV=nu RT] если удалить 3 моль газа, то количество вещества уменьшится в 4 раза (nu_1=dfrac{nu}{4}), следовательно, температуру надо увеличить в 4 раза.
Ответ: 4
Источник
2011 год 109 вариант СЗ
В сосуде лежит кусок льда. Температура льда t1 = 0°С. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20°С? Тепловыми потерями на нагрев сосуда пренебречь.
(Решение)
2011 год. 01-2 вариант. С3
В бутылке объемом V = 1 л находится гелий при нормальном атмосферном давлении. Горлышко бутылки площадью S = 2 см2 заткнуто короткой пробкой, имеющей массу m = 20 г. Если бутылка лежит горизонтально, то для того, чтобы медленно вытащить из ее горлышка пробку, нужно приложить к пробке горизонтально направленную силу F = 1 Н. Бутылку поставили на стол вертикально горлышком вверх. Какое количество теплоты нужно сообщить гелию в бутылке для того, чтобы он выдавил пробку из горлышка? (Решение)
2011 год. 01-1 вариант. С3
Один моль идеального одноатомного газа переводят из состояния 1 с температурой Т1 = 300 К в состояние 2 таким образом, что в течение всего процесса давление газа возрастает прямо пропорционально его объему. В ходе этого процесса газ получает количество теплоты Q = 14958 Дж. Во сколько раз n уменьшается в результате этого процесса плотность газа? (Решение)
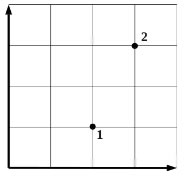 2010 год. 11 вариант. С1
2010 год. 11 вариант. С1
В кабинете физики проводились опыты с разреженным газом постоянной массы. По невнимательности ученик, отметив на графике начальное и конечное состояния газа (см. рисунок), не указал, какие две величины из трёх (давление р, объём V, температура Т) отложены по осям. В журнале осталась запись, согласно которой названные величины изменялись следующим образом: p1 < р2, V1 > V2, Τ1 < Ί2. Пользуясь этими данными, определите, какие величины были отложены на горизонтальной и вертикальной осях. Ответ поясните, указав, какие физические закономерности вы использовали. (Решение)
 2010 год
2010 год
304 вариант СЗ
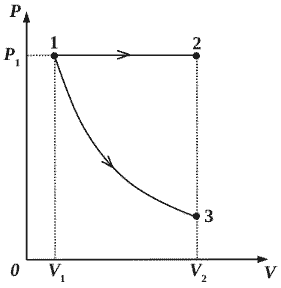
Некоторое количество одноатомного идеального газа расширяется из одного и
того же начального состояния (p1, V1) до одного и того же конечного объёма V2
первый раз по изобаре, а второй – по адиабате (см. рисунок). Отношение количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа |U3 — U1| на адиабате k = Q12/|U3 — U1| = 6 . Чему равно
отношение х работы газа на изобаре А12 к работе газа на адиабате А13? (Решение)
 2010 год. 135 вариант. С5
2010 год. 135 вариант. С5
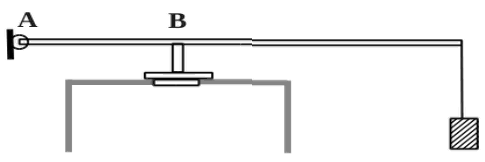
В цилиндр закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие площадью 5·10-4 м2, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии невесомым стержнем длиной 0,5 м, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). Расстояние АВ равно 0,1 м. К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через
580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите объём цилиндра. (Решение)
2009 год. 133 вариант. С1
В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
жидкости в сосуде? Ответ поясните. (Решение)
 2009 год. 133 вариант. С3
2009 год. 133 вариант. С3
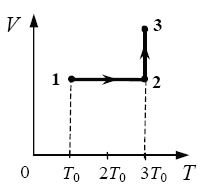
Один моль одноатомного идеального газа
переходит из состояния 1 в состояние 3 в
соответствии с графиком зависимости его объёма
V от температуры T (T0 = 100 К). На участке 2 − 3
к газу подводят 2,5 кДж теплоты. Найдите
отношение работы газа А123 ко всему количеству
подведенной к газу теплоты Q123. (Решение)
 2009 год. 304 вариант. С3
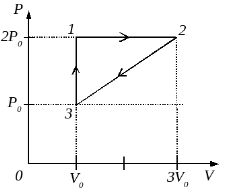
2009 год. 304 вариант. С3
Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты QH = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3?
(Решение)
 2008 год. 131 вариант. С2
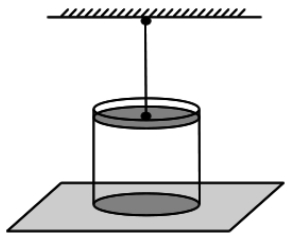
2008 год. 131 вариант. С2
Разогретый сосуд прикрыли поршнем, который с помощью вертикальной нерастяжимой нити соединили с потолком. На сколько процентов от начальной понизится температура воздуха в сосуде к моменту, когда сосуд оторвется от поверхности, на которой он расположен? Масса сосуда 5 кг. Поршень может скользить по стенкам сосуда без трения. Площадь дна сосуда 125 см2. Атмосферное давление 105 Па. Тепловым расширением сосуда и поршня пренебречь. (Решение)
2008 год. 5941 вариант. С2
В калориметре находился m1 = 1 кг льда при температуре t1 = -5°С. После добавления в калориметр m2 = 25 г воды в нем установилось тепловое равновесие при температуре t = 0°С. Какова температура t2 добавленной в калориметр воды, если в калориметре оказался в итоге только лёд? Теплоёмкостью калориметра пренебречь. (Решение)
2008 год. 05205939 вариант. С2
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз. На сколько градусов следует нагреть воздух в трубке, чтобы объём, занимаемый воздухом, стал прежним? Температура воздуха в лаборатории 300 К, а атмосферное давление составляет 750 мм рт.ст. (Решение)
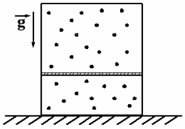 2008 год. 2 вариант. С2
2008 год. 2 вариант. С2
Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество водорода при температуре 361 К. Какая масса газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь. (Решение)
2007 год. 19 вариант. С2
В сосуде находится одноатомный идеальный газ, масса которого 12 г, а молярная масса 0,004 кг/моль. Вначале давление в сосуде было равно 4•105 Па при температуре 400 К. После охлаждения газа давление понизилось до 2•105 Па. Какое количество теплоты отдал газ? (Решение)
2006 год. 61 вариант. С2
В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м3- мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
2006 год. 86 вариант. С2
Теплоизолированный сосуд объемом V = 2 м3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль гелия, а в другой – такое же количество молей аргона. Начальная температура гелия равна 300 К, а температура аргона 600 К. Определите давление смеси после удаления перегородки. Теплоемкостью сосуда пренебречь. (Решение)
2006 год. 33 вариант. С2
Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. При какой минимальной разности температур воздуха внутри шара и снаружи шар взлетит вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Оболочку шара считать нерастяжимой. (Решение)
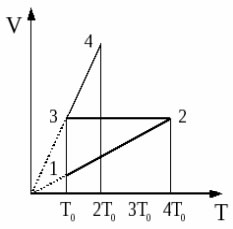
2006 год. 222 вариант. С2
С одним молем идеального одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке в координатах V-Т. Во сколько раз количество теплоты, полученное газом в процессе 1-2-3-4, больше работы газа в этом процессе? (Решение)
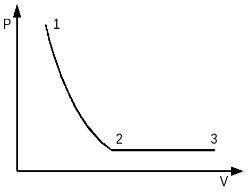 2005 год. 58 вариант. С2
2005 год. 58 вариант. С2
Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился при температуре T1 = 300 К. Затем газ изобарно нагрели, повысив температуру в 3 раза. Какое количество теплоты получил газ на участке 2-3? (Решение)
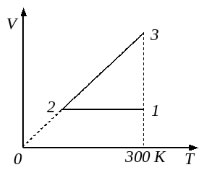
2004 год. 92 вариант. С2
10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2-3? (Решение)
 2004 год. 77 вариант. С5
2004 год. 77 вариант. С5
Идеальный одноатомный газ используется в качестве рабочего тела в тепловом двигателе. В ходе работы двигателя состояние газа изменяется в соответствии с циклом, состоящим из двух адиабат и двух изохор (см. рисунок). Вычислите КПД такого двигателя. (Решение)
2004 год. 49 вариант. С5
При электролизе воды образуется кислород О2 и водород Н2. Газы отводят в сосуд объёмом 100 л, поддерживая в нём температуру 300 К. Чему равна масса воды, которая разложилась в результате электролиза, чтобы суммарное давление в сосуде достигло 0,1 атм? Считать, что ничего не взрывается.
(Решение)
2004 год. 35 вариант. С5
Смесь одинаковых масс гелия, водорода и азота помещена в сосуд и нагрета до температуры 350 К. Плотность смеси оказалась равной 50 г/м3. Чему равно давление в сосуде? (Решение)
Источник
