В одну половину замкнутого сосуда поместили газ
1. Подберите синоним слову информация.
2. Минимальная единица количества информации.
3.В одну половину замкнутого сосуда поместили газ. Через некоторое время в результате беспорядочного движения молекулы газа заполнили весь сосуд. При этом…
4. Что такое «тепловая смерть»?
5. Информация о результате падения монеты приводит к уменьшению неопределенности знания в …
6. Количество информации – это…
7. Свойства информации.
8. Начерти систему управления, регулирующую температуру.
9. Соответствие группы знаков знаковой системе:
[л’], [j]+[а], [в], [э] а) Письменный русский язык
a,g,c,t б) Двоичная система счисления
A,G,C,T в) Письменный английский язык
0,1,2,3 г) Генетический алфавит
ц,я,н,э д) Устный русский язык
е) Десятичная система счисления
Какие знаки используются в человеческом общении?
Что такое кодирование информации?
Двоичное кодирование одного из 256 символов требует количества информации …
Один байт содержит… бит.
Соответствие устройства компьютера выполняемому действию:
Процессор
Устройства ввода информации
Оперативная память
Долговременная память
Устройства вывода информации
а) «Перевод» информации с языка человека на язык компьютера
б) Долговременное хранение данных
в) Обработка данных в соответствии с заданной программой
г) Обработка текущей информации и загрузка программ
Определите количество информации в книге, набранной на компьютере. Книга содержит 2500 страниц. На каждой странице- 30 строк, в каждой строке — 50 символов. Запиши ответ Мбайтах.
Сколько символов содержит сообщение, записанное с помощью 256-символьного алфавита, если объем его составил 1/32 часть Мбайта?
Какое количество информации несет код 0101110011110010010?
Наибольшее количество информации человек получает с помощью…
Сколько информации несет сообщение о том, что было угадано число в диапазоне целых чисел от 684 до 811?
Для кодирования нотной записи используется 7 значков-нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот?
Переведите:
15 Кбайт = ________байт
7168 байт = _______Кбайт
2 Мбайта = _______Кбайт
Сравните (поставьте знак отношения):
200 байт и 0,25 Кбайта
1000 битов и 1 Кбайт
Оценивание:
От 51 до 60 % заданий – «3» – от 11 правильных до 12,5
От 61 до 84 % заданий – «4» – от 13 правильных до 18
От 85 до 100 % заданий – «5» – от 19 правильных до 21
Ответы:
Сведения
Бит
произошел переход из менее вероятного упорядоченного состояния в более вероятное хаотическое состояние
молекулы и атомы со временем равномерно распределятся в пространстве и какие-либо изменения и развитие прекратятся
в 2 раза
мера уменьшения неопределенности знания при получении информационного сообщения
Достоверная, потная, точная, актуальная, полезная
команды управления
информация о величине температуры
Управляющее устройство
Нагревательный элемент с датчиками температуры
ответ
Ответ: 1-д, 2-в, 3-г, 4-е, 5-а
Зрительные, осязательные, слуховые
Процесс представления информации в виде кода
1 байт
8 бит
Ответ: 1-в, 2-а, 3-г, 4-б.
N=256 (т.к. текст набран на компьютере – мощность такого алфавита стандартна), i=8 бит, К=2500*30*50=3 750 000 символов в книге, I=i*K=8*3 750 000=30 000 000 бит= 3 750 000байт=3662,11 Кбайт=3,58 Мбайт
i=8 бит, 1/32 Мбайта=32 Кбайт=32 768 байт=262 144 бит.
i=1 бит, т.к. двоичная система счисления, I=1*19 символов= 19 бит
зрение
811-684=128 (включая число 684), N=128, i=7 бит (2^7=128).
Ответ: 7 бит информации.Каждая нота кодируется 3 битами (2^2=4<7<2^3=8).
Информационный объем сообщения равен 180 х 3 = 540 бит.
Ответ: 540 бит.15360 байт, 7 Кбайт, 2048 Кбайт; < , <.
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд — со вторым, второй — с третьим. Первоначально давление газа в сосудах было равно соответственно (р, 3р) и (р). В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
1) При первой открывании и закрывании кранов, в соответствии законам Дальтона и Бойля-Мариотта, установившееся давление во втором и третьем сосудах будет [dfrac{3p}{2}+dfrac{p}{2}=2p] 2) При втором открывании и закрывании, с учетом тех же законов, установившееся давление в первом и втором будет равно [dfrac{2p}{2}+dfrac{p}{2}=1,5p] 3) Так как объем сосуда не изменился, а температура по условию постоянна, то в соответствии закону Клайперона – Менделеева [pV=nu R T Rightarrow nu=dfrac{pV}{RT}] Знаменатель остался прежним, а числитель увеличился, значит и количество газа увеличилось.
Ответ:
Сжиженные газы с низкими температурами кипения хранят в открытых теплоизолированных резервуарах при нормальном давлении, с контактом с атмосферой. При таком хранении потери на испарение, отнесённые к единице массы сжиженного газа, уменьшаются при увеличении объёма сосуда. Объясните причины вышеизложенного, основываясь на известных физических законах и закономерностях.
1) Даже при хорошей теплоизоляции невозможно устранить полностью подвод тепла к сжиженным газам, значит, будет некоторое испарение вещества, потому что температура кипения таких газов ниже температуры атмосферы и существует теплопроводность.
2) Так как существует испарение, то в закрытых сосудах будет повышаться давление, что приведет к взрыву, поэтому газ хранят в открытых сосудах.
3) Подвод тепла к газу через стенки сосуда пропорционален площади стенок сосуда, а его масса пропорциональна объему. Объем же в свою очередь пропорционален кубу размеров сосуда. Поэтому с увеличением объема уменьшается испарение на единицу массы.
Ответ:
Чтобы вода в резервуаре быстрее закипела, источник тепла всегда помещают внизу. Желая охладить кастрюлю с горячей водой как можно быстрее, кастрюлю поставили на лёд. Является ли такой способ эффективным? Ответ поясните, указав какие физические явления и закономерности вы использовали для объяснения.
Нет, неверно.
Нагреватель ставится внизу, потому что нагретые слои воды, как более легкие, поднимаются вверх и таким образом достигается наиболее эффективное перемешивание и нагревание всей воды (по такому же принципу работает батарея в комнате). При охлаждении же дело происходит как раз наоборот: более холодные слои воды, как более тяжелые, опускаются вниз. Поэтому если поместить холодильник внизу, то перемешивания не будет, и остывание будет идти очень долго. Для более быстрого охлаждения надо поместить лед сверху.
Ответ:
На рисунке изображены графики двух процессов, проведённых с идеальным газом при одном и том же давлении. Графики процессов представлены на рисунке. Почему изобара (I) лежит выше изобары (II)? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения. 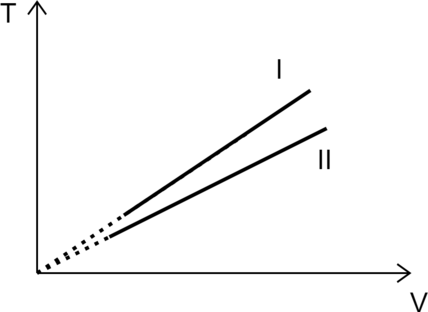
1. Идеальный газ подчиняется закону Клапейрона–Менделеева: [pV=nu R T,] где (p) – давление газа, (V) – объем, (nu) – количество газа, (T) – температура газа в Кельвинах.
Выразим температуру [T=dfrac{pV}{nu R}] 2. Зафиксируем объем (V_0), при этом отношение температур равно [dfrac{T_I}{T_{II}}=dfrac{dfrac{pV_0}{nu_I R}}{dfrac{pV_0}{nu{II}R}}=dfrac{nu_{II}}{nu_{I}}>1] Значит количество газа во втором больше, чем количество газа в первом.
Ответ:
1 моль разреженного гелия участвует в циклическом процессе 1–2–3–4–1, график которого изображён на рисунке в координатах V–T, где V — объём газа, Т — абсолютная температура. Постройте график цикла в координатах p–V, где р — давление газа, V— объём газа. Опираясь на законы молекулярной физики и термодинамики, объясните построение графика. Определите, во сколько раз работа газа в процессе 2–3 больше модуля работы внешних сил в процессе 4–1. 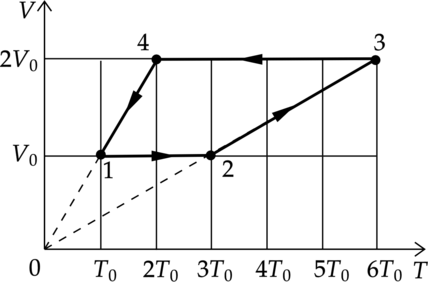
Проанализируем процессы:
1–2: Процесс изохорный, по закону Шарля (dfrac{p}{T}=const), температура увеличилась в 3 раза, значит и давление увеличилось в 3 раза.
2–3: Процесс изобарный, по закону Гей–Люсака (dfrac{V}{T}=const) и объем и температура увеличились в 2 раза.
3–4: В процессе 3–4 газ изохорно уменьшил свою абсолютную температуру и давление в 3 раза.
4–1: Газ вернулся в первоначальное состояние Перестроим график цикла в координатах p–V (см. рисунок). 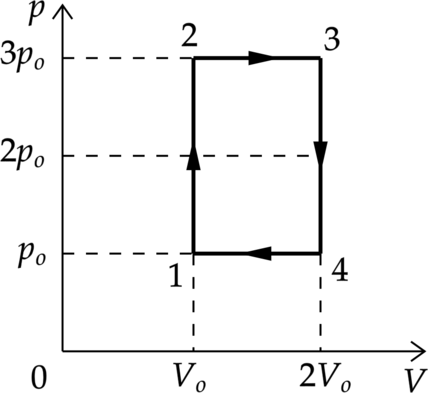
Работа газа в процессе 2–3 равна [A_{23}=pDelta V=3p_(2V_0-V_0)=3p_0V_0] Работа внешних сил в процессе 4–1 равна [|A_{41}|=pDelta V=p_0(2V_0-V_0)=p_0V_0] Значит работа газа в процессе 2–3 в 3 раза больше работы внешних сил в процессе 4–1.
Ответ:
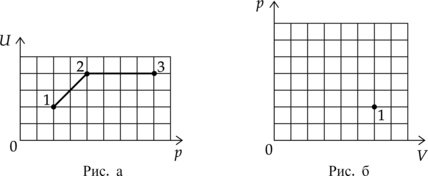
На рисунке 1 приведена зависимость внутренней энергии (U) 2 моль идеального одноатомного газа от его давления p в процессе 1–2–3. Постройте график этого процесса на рисунке 2 в переменных (p—V). Точка, соответствующая состоянию 1, уже отмечена на этом рисунке. Построение объясните, опираясь на законы молекулярной физики. 
1. Проанализируем процессы:
1–2: Внутренняя энергия прямо пропорциональна температуре газа (U=dfrac{3}{2}nu R T ), значит в процессе 1–2 температура увеличивается, давление тоже увеличивается (по графику ). По основному газовому закону (dfrac{pV}{T}=const) объем будет постоянен. График будет представлять собой вертикальную прямую
2–3: В процессе 2–3 внутренняя энергия газа постоянна, а значит и температура постоянна (по пункту 1), давление увеличивается, значит, по основному газовому закону объем будет уменьшаться. График будет представлять гиперболу.
2. Построим график

Ответ:
На графике представлена зависимость давления неизменной массы идеального газа от его плотности. Опишите, как изменяются в зависимости от плотности температура и объём газа в процессах 1–2 и 2–3. 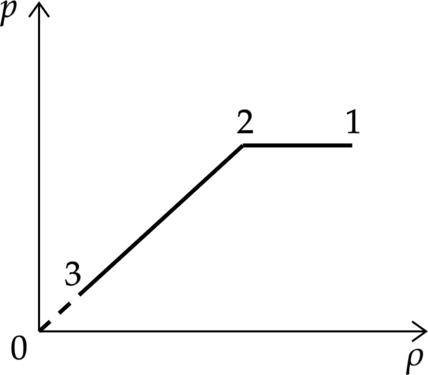
1. Плотность находится по формуле: [rho=dfrac{m}{V} quad (1)] тогда уравнение Клайперона–Менделеева можно переписать в виде [pV=dfrac{m}{mu}RT Rightarrow p=dfrac{rho}{mu}RT, quad (2)] где (m) – масса газа, (V) – его объем, (T) – температура газа. 2. Процесс 1–2.
Плотность уменьшается при постоянном, в соответствии с формулой (1) объем будет увеличиваться, а температура будет увеличиваться в соответствии с формулой (2).
Процесс 2–3.
Плотность уменьшается вместе с давлением, причем давление уменьшается пропорционально плотности (p sim rho), а это означает, что температура газа постоянна, а по формуле (1) объем увеличивается.
Ответ:
Источник
#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
2017-10-05
Сосуд с разреженным газом разделен на две части тонкой перегородкой, в которой имеется отверстие, размер которого мал по сравнению со средней длиной свободного пробега (рис. 1). Найти отношение концентрации газа в разных частях сосуда, если в одной из них поддерживается температура $T_{1}$, в другой $T_{2}$.

Решение:
Будем считать, что газ в сосуде идеальный, т. е. его молекулы взаимодействуют между собой только при столкновениях. По условию задачи газ разрежен настолько, что средняя длина свободного пробега молекул между столкновениями много больше размеров отверстия. В этом случае молекулы свободно проходят через отверстие, причем каждая молекула приходит в другую половину сосуда с той же энергией, которой она обладала до этого. Средняя энергия молекул при термодинамическом равновесии определяется температурой. Поэтому переход молекул из одной части сосуда в другую должен приводить к выравниванию температур.
Говорить об определенной температуре газа каждой части сосуда можно только в том случае, когда отверстие в перегородке достаточно маленькое, так что установление термодинамического равновесия в каждой части сосуда происходит гораздо быстрее, чем выравнивание температур этих частей.
Сколько же молекул проходит в единицу времени через отверстие из одной половины сосуда в другую? Нетрудно сообразить, что среднее число таких молекул $N$ пропорционально концентрации $n$ и средней скорости $langle v rangle$ молекул в той половине сосуда, из которой они переходят, а также площади отверстия $S$:
$N = Cn langle v rangle S$. (1)
Для вычисления числового значения безразмерного коэффициента $C$ нужно знать закон распределения молекул по направлениям скорости. Однако для решения этой задачи значение $C$ нам не потребуется.
В стационарном состоянии полное число молекул в каждой половине сосуда не меняется со временем. Поэтому среднее число молекул, проходящих через отверстие слева направо и справа налево, должно быть одинаковым. Отсюда с помощью соотношения (1) получаем
$n_{1} langle v_{1} rangle = n_{2} langle v_{2} rangle$. (2)
Средние скорости молекул в каждой половине пропорциональны квадратному корню из соответствующей температуры. Поэтому из равенства (2) находим
$n_{1}/n_{2} = sqrt{T_{2}/T_{1}}$. (3)
В горячей части сосуда концентрация молекул меньше. Однако давление газа там больше, чем в холодной части. Учитывая, что давление выражается формулой $p = nkT$, с помощью равенства (3) получаем для отношения давлений в разных половинах сосуда
$p_{1}/p_{2} = sqrt{T_{1}/T_{2}}$. (4)

рис.2
Рассмотренные в этой задаче закономерности, связанные с прохождением молекул газа через отверстие, соединяющее сосуды с разной температурой, позволяют объяснить следующий простой, но очень эффектный опыт. Керамический сосуд с пористыми стенками опускается открытым концом в воду (рис. 2). Внутри сосуда находится спираль, при пропускании тока через которую можно нагревать находящийся в сосуде воздух. При включении спирали температура воздуха повышается, он расширяется и начинает выходить пузырями из находящегося подводой отверстия сосуда. При достижении стационарного состояния , когда подводимая спиралью теплота станет равной теплоте, отдаваемой поверхностью сосуда в окружающую среду, в сосуде установится определенная температура. Казалось бы, что при этом выход пузырей воздуха должен прекратиться. Так бы и произошло, если бы стенки сосуда были непроницаемыми для молекул воздуха, например стеклянными или металлическими.
Но если стенки сосуда пористые, то пузырьки воздуха будут выходить все время, даже тогда, когда температура воздуха в сосуде перестанет повышаться! В чем же здесь дело?
Температура воздуха внутри пористого сосуда выше, чем снаружи, в атмосфере. Давление же воздуха там и там практически одинаково: внутри сосуда оно больше атмосферного всего на несколько сантиметров водяного столба, что соответствует глубине погружения отверстия сосуда код воду. Через поры в стенках сосуда происходит непрерывный обмен молекулами между воздухом внутри сосуда и в атмосфере, так же как это происходит в сосуде с отверстием в перегородке, рассмотренным в данной задаче. В замкнутом сосуде в стационарном состоянии число молекул, проходящих через отверстие в обе стороны, одинаково. В результате, как видно из формулы (3), в частях сосуда устанавливались такие концентрации, что произведение концентрации на корень из термодинамической температуры было одинаково: $n sqrt{T} = const$.
В рассматриваемом случае одинаковыми по обе стороны пористой перегородки будут давления воздуха. Так как $p = nkT$, то теперь $nT = const$. Но это означает, что потоки молекул воздуха через поры в стенках из атмосферы в сосуд и обратно неодинаковы. Какой же из них больше? Так как поток молекул пропорционален произведению $n sqrt{T}$ в той части, откуда он идет, то при выполнении условия $nT = const$ он будет больше оттуда, где температура ниже. Это и дает объяснение описанному опыту: поток воздуха через поры внутрь сосуда больше, чем наружу. В результате в стационарном состоянии входящий через поры в сосуд избыточный воздух нагревается, расширяется и выходит в виде пузырей через отверстие.
Источник
