В открытый цилиндрический сосуд
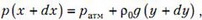
1. Пусть – давление азота в камере;
– давление в сосуде в ситуации на рис. ;
– давление в сосуде при температуре в конце опыта;
– площадь горизонтального сечения сосуда.
2. Параметры азота в сосуде в первоначальном состоянии и при
температуре связаны равенством, следующим из уравнения
Клапейрона-Менделеева:
откуда
Условие равновесия пробки при температуре :
откуда
3. Параметры азота в сосуде в первоначальном и конечном состояниях
тоже связаны равенством, следующим из уравнения Клапейрона-Менделеева:
откуда
Условие равновесия пробки в конечном состоянии:
откуда
4. Приравнивая друг другу два выражения для получаем равенство
Отсюда: K.
Возможны другие варианты решения.
Ответ: K.
Порядок назначения третьего эксперта
В соответствии с Порядком проведения государственной итоговой
аттестации по образовательным программам среднего общего образования
(приказ Минобрнауки России от зарегистрирован Минюстом России )
« По результатам первой и второй проверок эксперты независимо
друг от друга выставляют баллы за каждый ответ на задания
экзаменационной работы ЕГЭ с развёрнутым ответом…
В случае существенного расхождения в баллах, выставленных
двумя экспертами, назначается третья проверка. Существенное расхождение
в баллах определено в критериях оценивания по соответствующему
учебному предмету.
Эксперту, осуществляющему третью проверку, предоставляется
информация о баллах, выставленных экспертами, ранее проверявшими
экзаменационную работу».
Если расхождение составляет и более балла за выполнение задания, то третий эксперт проверяет ответ на задание.
Критерии оценки
3 баллаПриведено полное решение, включающее следующие элементы:
I.записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: уравнение
Клапейрона-Менделеева; условие равновесия тела, движущегося
поступательно);
II. описаны все вновь вводимые в решении буквенные
обозначения физических величин (за исключением обозначений
констант, указанных в варианте КИМ, обозначений, используемых
в условии задачи, и стандартных обозначений величин, используемых
при написании физических законов);
III. проведены необходимые математические преобразования
и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV. представлен правильный ответ с указанием единиц измерения
искомой величины
2 баллаПравильно записаны все необходимые положения теории,
физические законы, закономерности, и проведены необходимые
преобразования. Но имеются один или несколько из следующих
недостатков.
Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения (не
зачёркнуты; не заключены в скобки, рамку
и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или
вычислениях допущены ошибки, и (или) в математических
преобразованиях/вычислениях пропущены логически важные
шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в
записи единиц измерения величины)
1 баллПредставлены записи, соответствующие одному из следующих
случаев.
Представлены только положения
и формулы, выражающие
физические законы, применение которых необходимо для
решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения данной задачи (или утверждение, лежащее в основе
решения), но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения
данной задачи (или в утверждении, лежащем в основе решения),
допущена ошибка, но присутствуют логически верные
преобразования с имеющимися формулами, направленные на
решение задачи
0 балловВсе случаи решения, которые не соответствуют вышеуказанным
критериям выставления оценок в балла
Источник
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
Очевидно, что этот же объем равен
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
Из совместного решения полученных уравнений найдем объемы льда и стекла:
Из растаявшего льда образовалась вода объемом
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
или, если записать атмосферное давление в виде , где H0 = 774 мм:
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
а на третьем участке, для
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
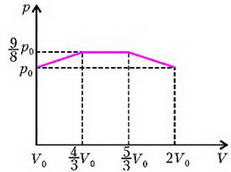
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
Запишем уравнение состояния гелия как идеального газа:
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
Продифференцируем обе части этого уравнения:
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
Поскольку начальная и конечная температуры равны, соответственно,
то изменение внутренней энергии равно
Полную работу найдем как площадь под кривой на рисунке 2:
Тогда окончательно
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
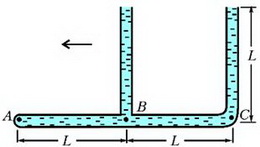
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
Решая эту систему относительно рА, найдем
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
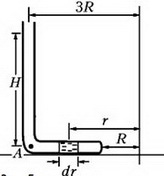
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
Проинтегрируем обе части этого уравнения и получим
Константу определим из условия, что при r = 3R (точка А) давление равно
и получим зависимость p(r)
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
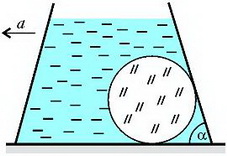
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
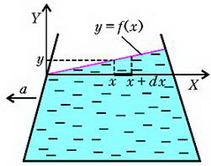
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
а с правого торца оно равно
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
Отсюда получаем
или в интегральном виде —
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
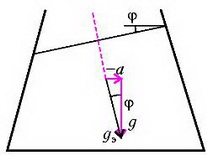
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
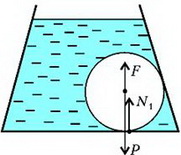
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
и по горизонтали:
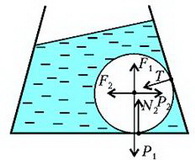
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.
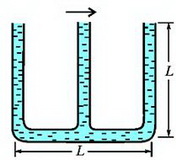
Рис. 11
4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.
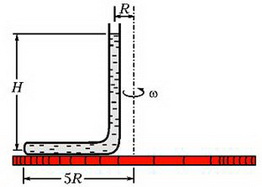
Рис. 12
Ответы.
1.
2.
3. .
4.
Источник
Задача по физике – 6814
В цилиндрический сосуд с площадью основания $S$, частично заполненный водой, пустили плавать шар объема $V$ с полостью внутри, так что шар погрузился наполовину. На сколько повысился уровень воды в сосуде? Как изменится уровень воды в сосуде после заполнения полости ($v_{полости} = 0,4V$) водой из этого же сосуда? Какая часть шара будет выступать из воды после заполнения полости?
Подробнее
Задача по физике – 6815
Два одинаковых цилиндрических сосуда на половине высоты соединены трубкой (см. рис.). Левый сосуд плотно закрыт крышкой с небольшим отверстием. Площадь дна каждого из цилиндров равна $0,03 м^{2}$, высота — 0,4 м. К крышке левого сосуда подвешен на нити деревянный кубик с ребром в 0,1 м. Нижняя грань кубика находится на уровне трубки. В правый сосуд с момента времени $t = 0$ равномерно наливают воду со скоростью $0,001 м^{3}/мин$. Нарисовать зависимость от времени давления воды на дно правого сосуда. Плотность воды — $10^{3} кг/м^{3}$, плотность дерева — $600 кг/м^{3}$. Вклад атмосферного давления можно не учитывать.

Подробнее
Задача по физике – 6816
Два одинаковых цилиндрических сосуда соединены внизу горизонтальной трубкой (сообщающиеся сосуды). В сосуды налили воду при $0^{ circ} С$ (см. рис.) и от левого стали отводить тепло, так что в нем сверху образовалась пробка льда цилиндрической формы. Верхняя плоскость ледяной пробки осталась на начальном уровне воды (лед примерз к стенкам), а нижняя граница до соединительной трубки не дошла. Найти вертикальную составляющую силы, действующей на лед со стороны стенок, если его масса равна $m$. Плотности воды и льда считать известными.

Подробнее
Задача по физике – 6817
Ртуть, частично заполняющая два цилиндрических стеклянных сосуда с сечениями $S$ и $2S$, соединенных резиновой трубкой, используется как часть электрической цепи (см. рис.). Подводящие провода пропущены через легкие поплавки и слегка погружены в ртуть. На сколько изменится сопротивление цепи, если узкий цилиндр приподнять на высоту $h$? Считать, что ртуть не переливается полностью из одного цилиндра в другой и не выливается через край. Удельное сопротивление ртути $rho$ считать известным.

Подробнее
Задача по физике – 6818
Правильный треугольник, изготовленный из трех шарнирно соединенных линеек, прислонили к вертикальной стене и поставили на горизонтальный стол. Найти силу взаимодействия наклонных линеек в шарнире А(см.рис.),если их массы равны $m$ и $2m$.

Подробнее
Задача по физике – 6847
Горизонтально расположенная трубка АВ длины $l$ вращается с постоянной угловой скоростью $omega$ вокруг неподвижной вертикальной оси $OO^{ prime}$, проходящей через конец А (рис.). В трубке находится идеальная жидкость. Конец А трубки открыт, а в закрытом конце В имеется очень малое отверстие. Найти, с какой скоростью относительно трубки будет вытекать жидкость в зависимости от «высоты» ее столба $h$.

Подробнее
Задача по физике – 6848
Показать, что в случае стационарного потока идеальной жидкости уравнение $rho frac{d vec{v}}{dt} = vec{f} – nabla p$ приводит к уравнению Бернулли.
Подробнее
Задача по физике – 6849
С противоположных сторон широкого вертикального сосуда, наполненного водой, открыли два одинаковых отверстия, каждое площадью $S = 0,50 см^{2}$. Расстояние между ними по высоте $Delta h = 51 см$. Найти результирующую силу реакции вытекающей воды.
Подробнее
Задача по физике – 6850
В боковой стенке широкого цилиндрического вертикального сосуда высоты $h = 75 см$ сделана узкая вертикальная щель; нижний конец которой упирается в дно сосуда. Длина щели $l = 50 см$, ширина $b = 1,0 мм$. Закрыв щель, сосуд наполнили водой. Найти результирующую силу реакции вытекающей воды непосредственно после того, как щель открыли.
Подробнее
Задача по физике – 6851
Вода вытекает из большого бака по изогнутой под прямым углом трубке, внутренний радиус которой $r = 0,50 см$ (рис.). Длина горизонтальной части трубки $l = 22 см$. Расход воды $Q = 0,50 л/с$. Найти момент сил реакции воды на стенки этой трубки относительно точки О, обусловленный течением воды.

Подробнее
Задача по физике – 6852
В боковой стенке широкого открытого бака вмонтирована суживающаяся трубка (рис.), через которую вытекает вода. Площадь сечения трубки уменьшается от $S = 3,0 см^{2}$ до $s = 1,0 см^{2}$. Уровень воды в баке на $h = 4,6 м$ выше уровня в трубке. Пренебрегая вязкостью воды, найти горизонтальную составляющую силы, вырывающей трубку из бака.

Подробнее
Задача по физике – 6853
Цилиндрический сосуд с водой вращают вокруг его вертикальной оси с постоянной угловой скоростью $omega$. Найти:
а) форму свободной поверхности воды;
б) распределение давления воды на дне сосуда вдоль его радиуса, если давление в центре дна равно $p_{0}$.
Подробнее
Задача по физике – 6854
Тонкий горизонтальный диск радиуса $R = 10 см$ расположен в цилиндрической полости с маслом, вязкость которого $eta = 0,08 П$ (рис.). Зазоры между диском и горизонтальными торцами полости одинаковы и равны $h = 1,0 мм$. Найти мощность, которую развивают силы вязкости, действующие на диск, при вращении его с угловой скоростью $omega = 60 рад/с$. Краевыми эффектами пренебречь
Подробнее
Задача по физике – 6855
Длинный цилиндр радиуса $R_{1}$ перемещают вдоль его оси с постоянной скоростью $v_{0}$ внутри коаксиального с ним неподт вижного цилиндра радиуса $R_{2}$. Пространство между цилиндрами заполнено вязкой жидкостью. Найти скорость жидкости в зависимости от расстояния $r$ до оси цилиндров. Течение ламинарное.
Подробнее
Задача по физике – 6856
Жидкость с вязкостью $eta$ находится между двумя длинными коаксиальными цилиндрами с радиусами $R_{1}$ и $R_{2}$, причем $R_{1} а) угловую скорость вращающейся жидкости в зависимости от радиуса $r$.
б) момент сил трения, действующих на единицу длины внешнего цилиндра.
Подробнее
Источник
