В прямоугольном сосуде с непроницаемыми стенками
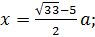
Задача 1
Для изменения собственного объема сыпучего материала его помещают в цилиндр, который герметически закрывают поршнем. Затем измеряют давление воздуха при одной и той же температуре и двух положениях поршня, когда суммарный объем воздуха и материала равен . Каков объем материала по этим данным?
Ответ:
Задача 2
На два длинных цилиндрических мешка радиуса r и длины , сделанных из нерастяжимого материала и заполненных газом, положили плиту массы m, в результате чего они сплющились до толщины . Внешнее давление . Определите начальное давление в мешках, если температура газа в них не изменялась.
 Ответ:
Ответ:
Задача 3
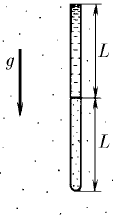
Нижний конец вертикальной узкой трубки 2 L запаян, а верхний открыт в атмосферу. В нижней половине трубки находится газ при температуре , а верхняя ее половина заполнена ртутью. До какой минимальной температуры надо нагреть газ в трубке, чтобы он вытеснил всю ртуть? Внешнее давление в миллиметрах ртутного столба равно L.
Ответ:
Задача 4
За сколько ходов поршневого насоса с рабочим объемом V можно понизить давление в сосуде вместимости с атмосферного до P?
Ответ:
Задача 5
Газовый термометр состоит из двух одинаковых сосудов вместимости каждый, соединенных трубкой длины l и сечения S. Трубку перекрывает капля ртути. Сосуды наполнены газом. Если температура газа в обоих сосудах одинакова, ртуть находится посередине трубки. Один сосуд помещен в термостат с температурой . Проградируйте термометр, найдя зависимость температуры газа во втором сосуде от смещения ртути из положения равновесия.
Ответ:
 Задача 6
Задача 6
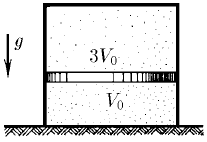
В цилиндрическом сосуде с газом находится в равновесии тяжелый поршень. Масса газа и его температура над поршнем и под ним одинакова. Отношение внутреннего объема верхней части сосуда к внутреннему объему нижней части равно 3. Каким будет это соотношение, если температуру газа увеличить в два раза?
Ответ:
Задача 7
На поверхности жидкости плотности ρ плавает цилиндрический тонкостенный стакан, наполовину погруженный в жидкость. На сколько погрузится стакан в жидкость, если его поставить на поверхность жидкости вверх дном? Высота стакана h, давление воздуха .
Ответ:
Задача 8
В прямоугольном сосуде с непроницаемыми стенками находится слева тяжелая жидкость, отделенная подвижным тонким поршнем от воздуха в правой части сосуда. В начальный момент поршень находится в равновесии и делит объем сосуда пополам. На сколько смещается поршень вправо, если температура системы уменьшится в три раза? Тепловым расширением жидкости и стенок сосуда пренебречь. Трения нет. Длина сосуда 2 a.
Ответ:
Задача 9
Воздух внутри оболочки воздушного шара вместимости V нагревается газовой горелкой до температуры T, превышающей температуру окружающего воздуха. Какова при атмосферном давлении грузоподъемность этого воздушного шара? Молярная масса воздуха µ.
Ответ:
Задача 10
Два мыльных пузыря радиуса сливаются в один. Найдите поверхностное натяжение мыльной воды, если радиус образовавшегося пузыря равен r, а атмосферное давление равно .
Ответ:
Дата: 2018-12-28, просмотров: 318.
Источник
Задача по физике – 6218
Кислород массой $m = 2 кг$ занимает объем $V_{1} = 1 м^{3}$ и находится под давлением $p_{1} = 0,2 МПа$. Газ был нагрет сначала при постоянном давлении до объема $V_{2} = 3 м^{3}$, а затем при постоянном объеме до давления $p_{3} = 0,5 МПа$. Найдите изменение $Delta U$ внутренней энергии газа, совершенную им работу $A$ и теплоту $Q$, переданную газу. Постройте графики процесса.
Подробнее
Задача по физике – 6219
В цилиндре под поршнем находится водород массой $m = 0,02 кг$ при температуре $T_{1} = 300 К$. Водород сначала расширился адиабатно, увеличив свой объем в $n_{1} = 5$ раз, а затем был сжат изотермически, причем объем газа уменьшился в $n_{1} = 5$ раз. Найдите температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах. Изобразите процесс графически.
Подробнее
Задача по физике – 6220
Два мыльных пузыря радиусами $R_{1}$ и $R_{2}$ сливаются в один пузырь радиуса $R$. Определите атмосферное давление. Коэффициент поверхностного натяжения мыльной пленки $sigma$.
Подробнее
Задача по физике – 6221
В герметически закрытом сосуде смешат одинаковое количество кислорода и гелия (моль на моль). Потом в стенке сосуда сделали маленькое отверстие. Найти состав молекулярного пучка, который выходит из отверстия.
Подробнее
Задача по физике – 6222
Баллон с газом разделён на две части термоизолирующей перегородкой с малым отверстием (ото означает, что молекул проходят в отверстие только «поодиночке», т. е. макроскопическое движение газа вблизи отверстия не может возникнуть). По разным сторонам перегородки всё время поддерживается температуры $T_{1}$ и $T_{2}$. Определите отношение давления $p_{1}$ и $p_{2}$ в различных част баллона.
Подробнее
Задача по физике – 6224
Внутри длинной трубы, наполненной воздухом, двигают с постоянной скоростью поршень, при этом по трубе распространяется упругая волна со скоростью $v = 320 м/с$. Считая перепад давлений на границе распространения волны равным 1000 Па, оцените перепад температур. Давление в невозмущенном воздухе 1 атм, температура 300 К.
Подробнее
Задача по физике – 6225
Идеальный газ постоянной массы расширяется по закону $p = alpha V$. Определить работу, выполненную газом при увеличении объёма от $V_{1}$ до $V_{2}$. Нагревается или охлаждается газ при таком процессе?
Подробнее
Задача по физике – 6226
В цилиндре под поршнем находится $nu$ молей ненасыщенного водяного пара при температуре $T_{0}$. При медленном изобарическом охлаждении цилиндра половина пара сконденсировалась, а внутренняя энергия содержимого цилиндра уменьшилась на $Delta U$. Какое количество теплоты пришлось при этом отвести от содержимого цилиндра, если температура в нем уменьшилась на $Delta T$? Объемом воды по сравнению с объемом пара можно пренебречь.
Подробнее
Задача по физике – 6227
Моль идеального одноатомного газа расширяется сначала в изобарическом процессе, а затем в процессе с линейной зависимостью давления от объема (рис.). Известно, что $V_{2}/V_{1} = V_{3} / V_{2}$, а прямая 2 -3 походит через начало координат. Найдите отношение объемов $V_{2}/V_{1}$, если количество теплоты, подведенное к газу на участке 1-2, в четыре раза меньше работы $A_{23}$, совершенной газом на участке 2-3.

Подробнее
Задача по физике – 6228
С одноатомным газом провели замкнутый процесс, состоящий из двух изохор и двух изобар (рис.). Определить $eta$ (КПД) теплового двигателя, работающего по этому циклу.

Подробнее
Задача по физике – 6229
Сообщающиеся цилиндры с поршнями площадью $S_{1}$ и $S_{2}$ (рис.) заполнены одноатомным газом с параметрами $p_{0}, V_{0}$ и $T_{0}$. Ни левый поршень действуют сила $F$, совершая работу $A$. Правый поршень сжимает упругую пружину жесткостью $k$. 1) Какое максимальное количество тепла $Q_{max}$ может при этом выделиться в окружающую среду? 2) До какой максимальной температуры может нагреться газ?

Подробнее
Задача по физике – 6330
На крыше, наклоненной к горизонту под углом $phi = 30^{ circ}$, лежит свинцовый лист массы $m$. Коэффициент трения свинца о крышу $k=0,7$ ($k > tg phi$). Длина листа при температуре $t_{1} = 10^{ circ} С l = 1 м$. Считая, что температура листа в течение суток повышается, достигая наивысшего значения $t_{2} = 20^{ circ} С$, а потом понижается до значения $t_{1}$, определить положение точек листа, неподвижных в течение суток при нагревании и при остывании. Найти расстояние, на которое сползет лист за $n = 30$ сут устойчивой погоды. Температурный коэффициент линейного расширения свинца $alpha = 3 cdot 10^{ – 5} К^{ -1}$.
Подробнее
Задача по физике – 6331
В запаянной с одного конца горизонтальной трубке сечения $S$ на расстоянии $l$ от запаянного конца находится поршень массы $m$. Другой конец трубки открыт, по обе стороны поршня – воздух, давление которого равно $p_{0}$. Трубку начинают вращать с угловой скоростью $omega$ вокруг вертикальной оси, проходящей через запаянный конец трубки. На каком расстоянии от запаянного конца трубки будет находиться поршень? Температуру воздуха считать постоянной, трением пренебречь.
Подробнее
Задача по физике – 6332
В U-образной трубке с воздухом на одинаковой высоте $h$ удерживают два поршня массы $m$ каждый (рис.). Площадь сечения левого колена трубки равна $2S$, площадь сечения правого колена и нижней части трубки равна $S$. Длина нижней части равна $3h$. Давление воздуха в трубке $p_{0}$ равно атмосферному. Поршни отпускают. Найти установившиеся высоты поршней. Поршни могут перемещаться только по вертикальным участкам трубки. Температуру воздуха считать постоянной.

Подробнее
Задача по физике – 6333
Прямоугольный сосуд с непроницаемыми стенками разделен вертикальным подвижным легким поршнем на две части: слева находится ртуть, справа – воздух. В начальный момент поршень находится в равновесии и делит сосуд на две равные части длины $l$. На сколько сместится поршень вправо после увеличения температуры (по шкале Кельвина) в три раза? Тепловым расширением ртути и сосуда, а также трением пренебречь.
Подробнее
Источник
Задача по физике – 6326
Струя воды в фонтане поднимается на высоту $H$ над уровнем выходной трубы насоса. К этой выходной трубе подсоединяют вертикальную трубу такого же диаметра, имеющую высоту $h 
Подробнее
Задача по физике – 6327
В вертикальной трубе радиуса $R$, заполненной жидкостью плотности $rho_{1}$, вдоль оси трубы всплывает круглый стержень радиуса $r$ и длины $l$, причем $l gg R$ (рис.). Плотность стержня $rho_{2}
Подробнее
Задача по физике – 6328
В короткой трубке переменного сечения поддерживается неизменное во времени течение вязкой несжимаемой жидкости плотности $rho$. В сечениях I и II, площади которых равны $S_{1}$ и $S_{2}$ соответственно, скорость жидкости можно, считать постоянной по сечению. Найти силу, с которой жидкость действует на участок трубы между сечениями I и II, и количество теплоты, которое выделяется в единицу времени в объеме трубы между этими сечениями. Давление и скорость жидкости в сечении I равны $p_{1}$ и $v_{1}$; в сечении II давление равно $p_{2}$.
Подробнее
Задача по физике – 6329
Труба радиуса $r$ заполнена пористой средой плотности $rho_{1}$. Невесомый поршень, на который действует сила $vec{F}$, вдвигаясь в трубу, уплотняет среду до плотности $rho_{2}$. С какой скоростью движется поршень, если уплотнение происходит скачком, т. е. по среде с некоторой скоростью перемещается поверхность $S$, по одну сторону от которой плотность среды равна $rho_{1}$, а по другую – равна $rho_{2}$? В начальный момент поверхность $S$ совпадает с поршнем.
Подробнее
Задача по физике – 6330
На крыше, наклоненной к горизонту под углом $phi = 30^{ circ}$, лежит свинцовый лист массы $m$. Коэффициент трения свинца о крышу $k=0,7$ ($k > tg phi$). Длина листа при температуре $t_{1} = 10^{ circ} С l = 1 м$. Считая, что температура листа в течение суток повышается, достигая наивысшего значения $t_{2} = 20^{ circ} С$, а потом понижается до значения $t_{1}$, определить положение точек листа, неподвижных в течение суток при нагревании и при остывании. Найти расстояние, на которое сползет лист за $n = 30$ сут устойчивой погоды. Температурный коэффициент линейного расширения свинца $alpha = 3 cdot 10^{ – 5} К^{ -1}$.
Подробнее
Задача по физике – 6331
В запаянной с одного конца горизонтальной трубке сечения $S$ на расстоянии $l$ от запаянного конца находится поршень массы $m$. Другой конец трубки открыт, по обе стороны поршня – воздух, давление которого равно $p_{0}$. Трубку начинают вращать с угловой скоростью $omega$ вокруг вертикальной оси, проходящей через запаянный конец трубки. На каком расстоянии от запаянного конца трубки будет находиться поршень? Температуру воздуха считать постоянной, трением пренебречь.
Подробнее
Задача по физике – 6332
В U-образной трубке с воздухом на одинаковой высоте $h$ удерживают два поршня массы $m$ каждый (рис.). Площадь сечения левого колена трубки равна $2S$, площадь сечения правого колена и нижней части трубки равна $S$. Длина нижней части равна $3h$. Давление воздуха в трубке $p_{0}$ равно атмосферному. Поршни отпускают. Найти установившиеся высоты поршней. Поршни могут перемещаться только по вертикальным участкам трубки. Температуру воздуха считать постоянной.

Подробнее
Задача по физике – 6333
Прямоугольный сосуд с непроницаемыми стенками разделен вертикальным подвижным легким поршнем на две части: слева находится ртуть, справа – воздух. В начальный момент поршень находится в равновесии и делит сосуд на две равные части длины $l$. На сколько сместится поршень вправо после увеличения температуры (по шкале Кельвина) в три раза? Тепловым расширением ртути и сосуда, а также трением пренебречь.
Подробнее
Задача по физике – 6334
В горизонтально закрепленной, открытой с торцов трубе сечения $S$ находятся два поршня. В исходном состоянии левый поршень соединен недеформированной пружиной жесткости $xi$ со стенкой, давление газа $p_{0}$ между поршнями равно атмосферному, расстояние $l$ от правого поршня до края трубы равно расстоянию между поршнями (рис.). Правый поршень медленно вытянули до края трубы. Какую силу надо приложить к поршню, чтобы удерживать его в этом положении? Температуру газа считать постоянной. Трением пренебречь.

Подробнее
Задача по физике – 6335
Цилиндрическая камера длины $2l$ с поршнем, площадь сечения которого равна $S$, может двигаться по горизонтальной плоскости с коэффициентом трения $k$ (рис.). Слева от поршня, расположенного в центре камеры, находится газ при температуре $T_{0}$ и давлении $p_{0}$. Между неподвижной стенкой и поршнем помещена пружина жесткости $xi$. Во сколько раз нужно увеличить температуру газа слева от поршня, чтобы объем этого газа удвоился, если трением между камерой и поршнем можно пренебречь? Масса камеры и поршня равна $m$. Наружное давление равно $p_{0}$.

Подробнее
Задача по физике – 6336
В цилиндрической трубе на расстояниях $L$ и $2L$ от закрытого торца находятся два поршня, которые могут перемещаться без трения (рис.). В левом отсеке находятся пары воды при давлении $p$, а в правом – воздух при том же давлении. Давление насыщенных паров воды равно $2p$. Правый поршень медленно вдвинули на расстояние $l$. На какое расстояние сдвинется левый поршень? Температуру паров воды и воздуха считать постоянной.
Подробнее
Задача по физике – 6337
Один моль идеального газа участвует в некотором процессе, изображенном в р,V-координатах (рис.). Продолжения отрезков прямых 1-2 и 3-4 проходят через начало координат, а кривые 1-4 и 2-3 являются изотермами. Изобразить этот процесс в Т, V -координатах и найти объем $V_{3}$, если известны объемы $V_{1}$ и $V_{2} = V_{4}$.
Подробнее
Задача по физике – 6338
В двух одинаковых колбах, соединенных трубкой, перекрытой краном, находится воздух при одинаковой температуре $T_{1} = T_{2}$ и разных давлениях. После того как кран открыли, часть воздуха перешла из одной колбы в другую. Через некоторое время давления в колбах сравнялись, движение газа прекратилось и температура в одной из колб стала равной $T_{1}$. Какой будет температура в другой колбе в этот момент? Внутренняя энергия одного моля воздуха $U=cT$. Объемом соединительной трубки пренебречь. Теплообмен со стенками не учитывать.
Подробнее
Задача по физике – 6339
Два цилиндра одинаковой длины $l$ и с площадью сечений: левого, равной $S$, и правого, равной $alpha S$ (рис.), соединены между собой. Посредине каждого цилиндра находятся поршни, соединенные жестким стержнем. Во всех трех отсеках системы находится идеальный газ. Давление в отсеке 1 равно $p$, а в отсеке 3 – равно $beta p$. Трение пренебрежимо мало, поршни находятся в равновесии. К системе подвели количество теплоты $Q$ так, что температура возросла, оставаясь во всех отсеках одинаковой. Определить изменение давления в отсеке 1. Внутренняя энергия одного моля газа равна $cT$. Теплоемкостью цилиндров и поршней пренебречь.

Подробнее
Задача по физике – 6340
В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем массы $M$, находится газ. Газ нагревают. Поршень, двигаясь равноускоренно, приобретает скорость $v$. Найти количество теплоты, сообщенной газу. Внутренняя энергия моля газа $U = cT$. Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь.
Подробнее
Источник
Задача по физике – 6323
Закрытый цилиндрический сосуд, наполненный на три четверти объема водой, вращается вокруг своей оси так, что в его центре образуется цилиндрическая полость. В воде плавает, погрузившись на две трети своей длины $l$, тонкий стержень АВ (рис.). Найти плотность стержня. Радиус цилиндра равен $R$, длина стержня $l 
Подробнее
Задача по физике – 6324
На поверхности воды плавает деревянный брусок квадратного сечения, имеющий плотность $rho = 0,5 cdot 10^{3} кг/м^{3}$. Какое из двух положений равновесия, показанных на рис., будет устойчивым и почему?

Подробнее
Задача по физике – 6325
Цилиндрический стакан до высоты $h$ заполнен кусочками льда. Поры между кусочками льда сквозные и в исходном состоянии заполнены воздухом. Льдинки занимают долю объема $alpha = 60$%. Лед начинает таять, причем соотношение объемов льдинок и пор между ними остается неизменным. Найти высоту уровня воды в стакане в момент, когда растаяла доля льда $beta = 70$ %. Плотность сплошного льда $rho = 0,9 cdot 10^{3} кг/м^{3}$, плотность воды $rho_{0} = 1 cdot 10^{3} кг/м^{3}$.
Подробнее
Задача по физике – 6326
Струя воды в фонтане поднимается на высоту $H$ над уровнем выходной трубы насоса. К этой выходной трубе подсоединяют вертикальную трубу такого же диаметра, имеющую высоту $h 
Подробнее
Задача по физике – 6327
В вертикальной трубе радиуса $R$, заполненной жидкостью плотности $rho_{1}$, вдоль оси трубы всплывает круглый стержень радиуса $r$ и длины $l$, причем $l gg R$ (рис.). Плотность стержня $rho_{2}
Подробнее
Задача по физике – 6328
В короткой трубке переменного сечения поддерживается неизменное во времени течение вязкой несжимаемой жидкости плотности $rho$. В сечениях I и II, площади которых равны $S_{1}$ и $S_{2}$ соответственно, скорость жидкости можно, считать постоянной по сечению. Найти силу, с которой жидкость действует на участок трубы между сечениями I и II, и количество теплоты, которое выделяется в единицу времени в объеме трубы между этими сечениями. Давление и скорость жидкости в сечении I равны $p_{1}$ и $v_{1}$; в сечении II давление равно $p_{2}$.
Подробнее
Задача по физике – 6329
Труба радиуса $r$ заполнена пористой средой плотности $rho_{1}$. Невесомый поршень, на который действует сила $vec{F}$, вдвигаясь в трубу, уплотняет среду до плотности $rho_{2}$. С какой скоростью движется поршень, если уплотнение происходит скачком, т. е. по среде с некоторой скоростью перемещается поверхность $S$, по одну сторону от которой плотность среды равна $rho_{1}$, а по другую – равна $rho_{2}$? В начальный момент поверхность $S$ совпадает с поршнем.
Подробнее
Задача по физике – 6330
На крыше, наклоненной к горизонту под углом $phi = 30^{ circ}$, лежит свинцовый лист массы $m$. Коэффициент трения свинца о крышу $k=0,7$ ($k > tg phi$). Длина листа при температуре $t_{1} = 10^{ circ} С l = 1 м$. Считая, что температура листа в течение суток повышается, достигая наивысшего значения $t_{2} = 20^{ circ} С$, а потом понижается до значения $t_{1}$, определить положение точек листа, неподвижных в течение суток при нагревании и при остывании. Найти расстояние, на которое сползет лист за $n = 30$ сут устойчивой погоды. Температурный коэффициент линейного расширения свинца $alpha = 3 cdot 10^{ – 5} К^{ -1}$.
Подробнее
Задача по физике – 6331
В запаянной с одного конца горизонтальной трубке сечения $S$ на расстоянии $l$ от запаянного конца находится поршень массы $m$. Другой конец трубки открыт, по обе стороны поршня – воздух, давление которого равно $p_{0}$. Трубку начинают вращать с угловой скоростью $omega$ вокруг вертикальной оси, проходящей через запаянный конец трубки. На каком расстоянии от запаянного конца трубки будет находиться поршень? Температуру воздуха считать постоянной, трением пренебречь.
Подробнее
Задача по физике – 6332
В U-образной трубке с воздухом на одинаковой высоте $h$ удерживают два поршня массы $m$ каждый (рис.). Площадь сечения левого колена трубки равна $2S$, площадь сечения правого колена и нижней части трубки равна $S$. Длина нижней части равна $3h$. Давление воздуха в трубке $p_{0}$ равно атмосферному. Поршни отпускают. Найти установившиеся высоты поршней. Поршни могут перемещаться только по вертикальным участкам трубки. Температуру воздуха считать постоянной.

Подробнее
Задача по физике – 6333
Прямоугольный сосуд с непроницаемыми стенками разделен вертикальным подвижным легким поршнем на две части: слева находится ртуть, справа – воздух. В начальный момент поршень находится в равновесии и делит сосуд на две равные части длины $l$. На сколько сместится поршень вправо после увеличения температуры (по шкале Кельвина) в три раза? Тепловым расширением ртути и сосуда, а также трением пренебречь.
Подробнее
Задача по физике – 6334
В горизонтально закрепленной, открытой с торцов трубе сечения $S$ находятся два поршня. В исходном состоянии левый поршень соединен недеформированной пружиной жесткости $xi$ со стенкой, давление газа $p_{0}$ между поршнями равно атмосферному, расстояние $l$ от правого поршня до края трубы равно расстоянию между поршнями (рис.). Правый поршень медленно вытянули до края трубы. Какую силу надо приложить к поршню, чтобы удерживать его в этом положении? Температуру газа считать постоянной. Трением пренебречь.

Подробнее
Задача по физике – 6335
Цилиндрическая камера длины $2l$ с поршнем, площадь сечения которого равна $S$, может двигаться по горизонтальной плоскости с коэффициентом трения $k$ (рис.). Слева от поршня, расположенного в центре камеры, находится газ при температуре $T_{0}$ и давлении $p_{0}$. Между неподвижной стенкой и поршнем помещена пружина жесткости $xi$. Во сколько раз нужно увеличить температуру газа слева от поршня, чтобы объем этого газа удвоился, если трением между камерой и поршнем можно пренебречь? Масса камеры и поршня равна $m$. Наружное давление равно $p_{0}$.

Подробнее
Задача по физике – 6336
В цилиндрической трубе на расстояниях $L$ и $2L$ от закрытого торца находятся два поршня, которые могут перемещаться без трения (рис.). В левом отсеке находятся пары воды при давлении $p$, а в правом – воздух при том же давлении. Давление насыщенных паров воды равно $2p$. Правый поршень медленно вдвинули на расстояние $l$. На какое расстояние сдвинется левый поршень? Температуру паров воды и воздуха считать постоянной.
Подробнее
Задача по физике – 6337
Один моль идеального газа участвует в некотором процессе, изображенном в р,V-координатах (рис.). Продолжения отрезков прямых 1-2 и 3-4 проходят через начало координат, а кривые 1-4 и 2-3 являются изотермами. Изобразить этот процесс в Т, V -координатах и найти объем $V_{3}$, если известны объемы $V_{1}$ и $V_{2} = V_{4}$.
Подробнее
Источник
